Course
Linear regression is a powerful tool in data analysis and data science. It is used to quantify the relationship between a dependent variable and one or more independent variables. If you are familiar with linear regression, you may also be familiar with the common goodness-of-fit measure called r-squared, which indicates the proportion of the variance in the dependent variable that is explained by the independent variable(s). However, you may be less familiar with adjusted r-squared, which is often used with more complex models with multiple predictors.
This article will give you a comprehensive understanding of adjusted r-squared, its importance in model evaluation, its key differences from r-squared, and its applications in multiple regression scenarios so you can have a full mastery of these model statistics. As we get started, I highly recommend taking DataCamp’s Introduction to Regression with statsmodels in Python course and our Introduction to Regression in R course to learn about regression models and how to interpret the different performance metrics, including adjusted r-squared.
What is Adjusted R-Squared?
R-squared measures the proportion of variance in the dependent variable explained by the model's independent variable or variables. The adjusted r-squared also explains the variance, but it has an additional consideration: As the name suggests, it adjusts the r-squared value by penalizing the inclusion of irrelevant, by which we mean highly collinear, variables. It does this by taking into account both the number of predictors and the sample size.
In order to find the adjusted r-squared, we have to first find the r-squared. Although there are different ways to find the r-squared value, the formula below is one of the most common:
Formula for r-squared
Here, the r-squared is calculated as one minus the quotient of the sum of squares residuals over the total sum of squares.
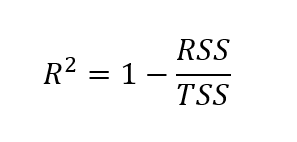
Where:
- RSS = Sum of squared residuals (the sum of the squared differences between observed and predicted values)
- TSS = Total sum of squares (the sum of the squared differences between observed values and the mean of the observed values)
Formula for adjusted r-squared
After finding the r-squared value, we can find the adjusted r-squared. We do this by inserting our r-squared value in the formula below.
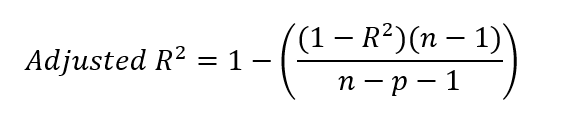
Where:
- R² = r-squared of the model
- n = number of observations (data points)
- p = number of predictors (independent variables)
To practice, we can try an example. Consider this scenario: We have a dataset with 30 observations. We create a multiple linear regression model with five predictors. We discover an r-squared of 0.8. Here is how we can take this information to find the adjusted r-squared:

You may be wondering about the -1 in the equation, both in the numerator and the denominator. To clarify, n−1 in the numerator accounts for the degrees of freedom, correcting for the use of the sample mean when calculating variance. This is because, when calculating variance, we typically use the sample mean as an estimate of the population mean. Because the sample mean is not the true population mean, the variance tends to be underestimated. To correct for this bias, we reduce the degrees of freedom by 1.
In the denominator, n−p−1 adjusts for the number of predictors p in the model, where p is the number of independent variables. The additional −1 in the denominator corrects for estimating the model's intercept, which also uses up one degree of freedom. We have to remember that, in a regression model, we estimate both the slope coefficients for the predictors and the intercept to account for the full complexity.
How Does Adjusted R-Squared Differ from R-Squared?
Although both r-squared and adjusted r-squared evaluate regression model performance, a key difference exists between the two metrics. The r-squared value always increases or remains the same when more predictors are added to the model, even if those predictors do not significantly improve the model's explanatory power. This issue can create a misleading impression of the model's effectiveness.
Adjusted r-squared adjusts the r-squared value to account for the number of independent variables in the model. The adjusted r-squared value can decrease if a new predictor does not improve the model's fit, making it a more reliable measure of model accuracy. For this reason, the adjusted r-squared can be used as a tool by data analysts to help them decide which predictors to include.
When to Use Adjusted R-Squared
Understanding when to use adjusted r-squared over r-squared is important in building reliable models. The following are scenarios where using adjusted r-squared to evaluate models is appropriate.
- Multiple Regression: Generally speaking, adjusted r-squared is a more reliable metric because it accounts for the number of predictors, ensuring a better evaluation of the model’s performance.
- Model Comparison: Adjusted r-squared is useful when comparing models with different numbers of predictors to choose the best-performing ones.
- To Prevent Overfitting: Adjusted r-squared helps by penalizing the inclusion of irrelevant predictors to ensure that only predictors that improve the model's performance are included.
In general, although adjusted r-squared is preferred over r-squared in multiple regression models because it accounts for the number of predictors and penalizes for adding irrelevant variables, there are some scenarios where using r-squared might still be appropriate:
- Simple Comparisons Between Models: If you're comparing models with the same number of predictors, r-squared can be used to measure the overall goodness of fit without worrying about overfitting, since both models have equal complexity.
- Explanatory Power Focus: If your goal is purely to understand how much of the variation in the dependent variable is explained by the independent variables, regardless of the number of predictors, r-squared can give a more straightforward interpretation.
Interpreting Adjusted R-Squared in Practice
Let's consider an example where the nuances between r-squared and adjusted r-squared would come into play. Suppose we have these two regression models:
- Model 1 has an r-squared of 0.9 and an adjusted r-squared of 0.75.
- Model 2 has an r-squared of 0.85 and an adjusted R-squared of 0.8.
We might say that model 1 seems to explain more of the overall variance in the data because it has a higher r-squared value. But we also have to consider that model 2 might explain more of the true underlying relationship between the variables because it accounts for irrelevant predictors. Model 2’s higher adjusted r-squared suggests that it provides a more reliable fit by penalizing for unnecessary complexity, and it might also be less prone to overfitting. Personally, and in the absence of other information, I would choose model 2.
Adjusted R-Squared in R and Python
Let us explore practical examples of calculating adjusted r-squared in R and Python. We will use the “Fish Market” dataset from Kaggle, which is useful for estimating a fish's weight based on its species and physical measurements. To simplify, we will round the output to five decimal places.
Adjusted r-squared in R
Download the dataset and save it in your working directory. Use the following code to fit a linear model to predict the weight of the fish as a function of a few different variables, including Length1, Height, Width, and Length3, which refers to the vertical length of the fish, the height of the fish, the diagonal width of the fish, and the cross length of the fish, respectively.
# Load the dataset
data <- read.csv("data/Fish.csv")
# Remove rows with missing values
data <- na.omit(data)
# Model 1: Using 4 predictors ('Length1', 'Height', 'Width', 'Length3')
model1 <- lm(Weight ~ Length1 + Height + Width + Length3, data = data)Now, we check the r-squared and adjusted r-squared values, and we see the following. The adjusted r-squared is very close to the r-squared value, just slightly slower.
r_squared_model1 <- round(summary(model1)$r.squared, 4)
r_squared_model1 <- round(summary(model1)$adj.r.squared, 4)0.88527
0.88229What if we now try to create another model by adding another predictor? This time, we create a second model and add Length2, which refers to the diagonal length of the fish. In the same way as before, we can check our new model's r-squared and adjusted r-squared values.
# Model 2: Adding one more predictor ('Length2')
model2 <- lm(Weight ~ Length1 + Height + Width + Length3 + Length2, data = data)r_squared_model2 <- round(summary(model1)$r.squared, 4)
r_squared_model2 <- round(summary(model1)$adj.r.squared, 4)0.88529
0.88154For model 2, we can see that the r-squared value for the barely increased at all when compared to model 1. Also, we see that the adjusted r-squared valued decreased, and the decrease in the adjusted r-squared was more than the increase in the r-squared value. This tells us the predictor we added was not a good one.
When we think about it, Length2, which refers to the diagonal length of the fish, was probably highly correlated with either the other variables in the model or a linear combination of the other variables in the model. In particular, we expect that the diagonal length of th fish is highly correlated with the length of the fish and the cross length of the fish. So we see our new variable didn’t add new, relevant information.
In the interest of thoroughness, we can also demonstrate how to find the adjusted r-squared by hand. We use the r-squared value and the model parameters, and we follow the formula we showed earlier.
# Save R-squared as a variable
r_squared_model2 <- summary(model2)$r.squared
# Get the number of observations (n) for both models
n <- nrow(data) # Same for both models
# Get the number of predictors (excluding intercept) for each model
p_model1 <- length(coef(model1)) - 1
p_model2 <- length(coef(model2)) - 1
# Adjusted r-squared formula for Model 1
adjusted_r_squared_model1 <- 1 - ((1 - r_squared_model1) * (n - 1)) / (n - p_model1 - 1)
# Adjusted r-squared formula for Model 2
adjusted_r_squared_model2 <- 1 - ((1 - r_squared_model2) * (n - 1)) / (n - p_model2 - 1)
# Print R-squared values for both models
cat("R-Squared for Model 1:", r_squared_model1, "\n")
cat("R-Squared for Model 2:", r_squared_model2, "\n")
# Print the Adjusted R-Squared values for both models
cat("Adjusted R-Squared for Model 1:", adjusted_r_squared_model1, "\n")
cat("Adjusted R-Squared for Model 2:", adjusted_r_squared_model2, "\n")Adjusted r-squared in Python
The following code shows an implementation of the same example in Python.
# Import requied libraries
import pandas as pd
import statsmodels.api as sm
# Load the dataset
data = pd.read_csv('data/Fish.csv')
# Drop rows with missing values if any exist
data = data.dropna()
# Define predictors for Model 1 (4 variables)
X1 = data[['Length1', 'Height', 'Width', 'Length3']]
# Add a constant (intercept)
X1 = sm.add_constant(X1)
# Define the target variable 'Weight'
y = data['Weight']
# Fit Model 1
model1 = sm.OLS(y, X1).fit()
# Define predictors for Model 2 (5 variables)
X2 = data[['Length1', 'Height', 'Width', 'Length3', 'Length2']]
# Add a constant (intercept)
X2 = sm.add_constant(X2)
# Fit Model 2
model2 = sm.OLS(y, X2).fit()
# Save r-squared as a variable
r_squared_model1 = model1.rsquared # R-Squared for Model 1
r_squared_model2 = model2.rsquared # R-Squared for Model 2
# Get the number of observations
n = X1.shape[0] # Same for both models
# Get the number of predictors (excluding intercept) for each model
p_model1 = X1.shape[1] - 1 # Number of predictors for Model 1
p_model2 = X2.shape[1] - 1 # Number of predictors for Model 2
# Adjusted R-Squared formula for Model 1
adjusted_r_squared_model1 = 1 - ((1 - r_squared_model1) * (n - 1)) / (n - p_model1 - 1)
# Adjusted R-Squared formula for Model 2
adjusted_r_squared_model2 = 1 - ((1 - r_squared_model2) * (n - 1)) / (n - p_model2 - 1)
# Print R-squared for both models
print("R-Squared for Model 1:", r_squared_model1)
print("R-Squared for Model 2:", r_squared_model2)
# Print the Adjusted R-Squared values for both models
print("Adjusted R-Squared for Model 1:", adjusted_r_squared_model1)
print("Adjusted R-Squared for Model 2:", adjusted_r_squared_model2)We can also use functions in Python to find the r-squared and adjusted r-squared values of the regression models:
# Model 1
print("Model 1 R-Squared:", model1.rsquared)
print("Model 1 Adjusted R-Squared:", model1.rsquared_adj)
# Model 2
print("Model 2 R-Squared:", model2.rsquared)
print("Model 2 Adjusted R-Squared:", model2.rsquared_adj)If you had any trouble with the code sections above, check out our tutorials on Essentials of Linear Regression in Python and How to Do Linear Regression in R to learn the step-by-step guide to implementing and interpreting different metrics of the regression model. If Excel is your preferred analysis tool, check out our tutorial on Linear Regression in Excel: A Comprehensive Guide For Beginners to learn how to implement and visualize linear regression models in Excel.
Adjusted R-Squared, R-Squared, and Predicted R-Squared
As we consider adjusted r-squared, we should take some time to keep our terms straight. There are some terms that seem similar but have different purposes. Here, I've created a table that compares some similar-sounding but distinct ideas: r-squared, adjusted r-squared, and predicted r-squared.
| Metric | Measures | Use Case | Strengths | Limitations |
|---|---|---|---|---|
| R-squared | Proportion of variance explained by the model | Understanding how well the model fits the training data | Simple to interpret and quickly provides model fit | Misleading when comparing models with different predictors, vulnerable to overfitting |
| Adjusted R-squared | Proportion of variance explained, adjusted for the number of predictors | Comparing models with different numbers of predictors | Penalizes for adding irrelevant variables, prevents overfitting | Does not indicate predictive performance on new data |
| Predicted R-squared | How well the model predicts new data | Evaluating model performance on unseen data | Indicates how well the model generalizes to new data | Requires cross-validation or a holdout dataset, computationally expensive |
Common Misconceptions About Adjusted R-Squared
Finally, let's look at some common mistakes because there are some common misunderstandings about its use in regression.
- A Low Adjusted R-Squared Means the Model is Poor: A low adjusted r-squared does not necessarily mean the model is bad or irrelevant. The low value may indicate that the independent variables in the model do not explain a large proportion of the variance in the dependent variable, but depending on the subject matter, that could be expected.
- Adjusted R-Squared Cannot Be Negative: Adjusted r-squared can technically be negative when the model explains an extremely low proportion of the variance in the dependent variable and at the same time uses many predictors, which results in penalties that create a situation with negative adjusted r-squared.
- Adjusted R-Squared Always Decreases When Adding Variables: Adjusted r-squared will decrease if the new variable does not improve the model’s performance but will increase if the new variable adds genuine value to the model. Imagine a model with one bad predictor, and then you add a good one; the adjusted r-squared will increase.
Final Thoughts on Adjusted R-Squared
Adjusted r-squared is an important metric for evaluating the performance of regression models, particularly when dealing with multiple independent variables. Compared to the r-squared metric, it provides a more realistic and reliable measure of model accuracy when multiple predictors are involved.
If you are curious about how R and Python find the coefficients of linear regression models, check out the following tutorials: Normal Equation for Linear Regression Tutorial and QR Decomposition in Machine Learning: A Detailed Guide.
Become an ML Scientist
Adjusted R-Squared FAQs
How does adjusted r-squared differ from r-squared?
While r-squared measures the proportion of variance in the dependent variable explained by the independent variables, it always increases when more predictors are added. Adjusted r-squared adjusts for the number of predictors and decreases if the additional variables do not contribute to the model’s significance.
When should I use adjusted r-squared?
Adjusted r-squared is useful when comparing the goodness-of-fit of regression models with different numbers of predictors or when you are concerned about overfitting.
Can the adjusted r-squared value be negative?
Adjusted r-squared can be negative when the model explains very little variance in the dependent variable and includes many predictors, leading to penalties that result in a negative value.
Why is the adjusted r-squared value always the same as or lower than the r-squared value?
Adjusted r-squared is always the same or lower than r-squared because it is designed to add a penalty for adding unnecessary predictors to the model.
When should I use predicted r-squared instead of adjusted r-squared?
Predicted r-squared is useful for assessing how well the model performs on new, unseen data.
What is the difference between adjusted f-squared and other linear regression model evaluation metrics like RMSE?
Adjusted r-squared measures the proportion of variance explained by the model, accounting for the number of predictors, while RMSE (Root Mean Squared Error) quantifies the average difference between observed and predicted values. In other words, RMSE focuses on prediction error, whereas adjusted r-squared focuses on model fit.
Does adjusted r squared only apply to linear regression?
Yes, adjusted r-squared is primarily associated with multiple linear regression models. For non-linear models like exponential and logarithmic functions, other metrics like AIC or BIC are typically used to penalize model complexity and assess goodness of fit.
What does it mean if the r-squared and the adjusted r-squared values from a linear regression model are very different?
A large difference between r-squared and adjusted r-squared suggests that the model includes irrelevant predictors. The adjusted r-squared penalizes for unnecessary variables, so if you see a big difference between the two, you may have predictors that are strongly correlated.
Is r-squared and adjusted r-squared the same in simple linear regression?
In simple linear regression, meaning regression with one dependent variable and only one independent variable, the r-squared and adjusted r-squared would be the same.

