Kurs
Die korrekte Aufbereitung deiner Daten ist sowohl für die Leistung der Modelle als auch für die Interpretation der Ergebnisse wichtig. Das ist die zentrale Herausforderung, bei der Normalisierung und Standardisierung ins Spiel kommen - zwei wesentliche Techniken zur Skalierung von Merkmalen, die verwendet werden können, um Daten für eine bessere Leistung anzupassen oder bei der Interpretation der Ergebnisse zu helfen.
In diesem Artikel werde ich dir die verschiedenen Begriffe erklären und dir helfen, die praktischen Unterschiede zwischen Normalisierung und Standardisierung zu erkennen. Am Ende wirst du wissen, wann du sie in deinem Datenvorverarbeitungs-Workflow einsetzen solltest. Wenn du dich mit Normalisierung und Standardisierung vertraut machst, kannst du die Leistung deiner Modelle steigern, die Ergebnisse besser interpretieren und häufige Fallstricke vermeiden, die mit nicht skalierten Daten einhergehen. Die feinen Unterschiede hier sind im Bereich des maschinellen Lernens sehr wichtig. Wenn du wirklich ein Experte werden willst, dann melde dich noch heute für unseren Berufswunsch Machine Learning Scientist in Python an.
Werde ein ML-Wissenschaftler
Die Skalierung von Merkmalen verstehen
Sowohl die Normalisierung als auch die Standardisierung gehören zur Idee oder Kategorie der Merkmalsskalierung. Die Skalierung von Merkmalen ist ein wichtiger Schritt bei der Vorbereitung von Daten für maschinelle Lernmodelle. Dabei werden die Werte der Merkmale in einem Datensatz in eine ähnliche Skala umgewandelt, um sicherzustellen, dass alle Merkmale gleichermaßen zum Lernprozess des Modells beitragen.
Die Skalierung von Merkmalen ist wichtig, dennwenn Merkmale auf sehr unterschiedlichen Skalen liegen, z. B. ein Merkmal von 1 bis 10 und ein anderes von 1.000 bis 10.000, können die Modelle die größeren Werte bevorzugen, was zu Verzerrungen bei den Vorhersagen führt. Dies kann zu einer schlechten Modellleistung und einer langsameren Konvergenz beim Training führen.
Die Merkmalsskalierung löst diese Probleme, indem sie den Bereich der Daten anpasst, ohne die Unterschiede in den Werten zu verzerren. Es gibt verschiedene Skalierungstechniken, wobei die Normalisierung und Standardisierung am häufigsten verwendet werden. Beide Methoden helfen maschinellen Lernmodellen, optimal zu funktionieren, indem sie die Auswirkungen von Merkmalen ausbalancieren, den Einfluss von Ausreißern reduzieren und in einigen Fällen die Konvergenzraten verbessern.
Was ist Normalisierung?
Normalisierung ist ein weit gefasster Begriff, und es gibt verschiedene Möglichkeiten, Daten zu normalisieren. Im Allgemeinen bezieht sich die Normalisierung auf den Prozess der Anpassung von Werten, die auf verschiedenen Skalen gemessen wurden, an eine gemeinsame Skala. Manchmal ist es am besten, wenn du es mit einem Beispiel illustrierst. Für jede Art der Normalisierung werden wir im Folgenden ein Modell betrachten, um die Beziehung zwischen dem Preis eines Hauses und seiner Größe zu verstehen.
Arten der Normalisierung
Schauen wir uns einige der wichtigsten Arten an. Bedenke, dass diese Liste nicht vollständig ist:
Min-Max-Normalisierung
Mit der Min-Max-Normalisierung können wir die Größen der Häuser so skalieren, dass sie in einen Bereich von 0 bis 1 passen. Das bedeutet, dass die kleinste Hausgröße mit 0 und die größte Hausgröße mit 1 dargestellt wird.
Log-Normalisierung
Die Log-Normalisierung ist eine weitere Normalisierungstechnik. Mit der Log-Normalisierung wenden wir eine logarithmische Transformation auf die Hauspreise an. Diese Technik hilft, die Auswirkungen größerer Preise zu verringern, vor allem, wenn es zwischen ihnen große Unterschiede gibt.
Dezimale Skalierung
Die Dezimalskalierung ist eine weitere Normailzierungsmethode. In diesem Beispiel könnten wir die Größen der Häuser anpassen, indem wir den Dezimalpunkt verschieben, um die Werte kleiner zu machen. Das bedeutet, dass die Hausgrößen in einen handlicheren Maßstab umgewandelt werden, während ihre relativen Unterschiede erhalten bleiben.
Mittelwert-Normalisierung (Mittelwert-Zentrierung)
Die Normalisierung des Mittelwerts würde in diesem Zusammenhang bedeuten, dass die Hauspreise angepasst werden, indem der Durchschnittspreis von den Preisen der einzelnen Häuser abgezogen wird. Dieser Prozess zentriert die Preise auf Null und zeigt, wie die Größe der einzelnen Häuser im Vergleich zum Durchschnitt ist. Auf diese Weise können wir analysieren, welche Hausgrößen größer oder kleiner als der Durchschnitt sind, was die Interpretation ihrer relativen Preise erleichtert.
Wann solltest du Daten normalisieren?
Wie du vielleicht aus den obigen Beispielen entnommen hast, ist die Normalisierung besonders nützlich, wenn die Verteilung der Daten unbekannt ist oder nicht einer Gauß-Verteilung folgt. Hauspreise sind hier ein gutes Beispiel, denn manche Häuser sind sehr, sehr teuer, und Modelle kommen mit Ausreißern nicht immer gut zurecht.
Das Ziel der Normalisierung ist es also, ein besseres Modell zu erstellen. Wir könnten die abhängige Variable normalisieren, damit die Fehler gleichmäßiger verteilt sind, oder wir könnten die Eingangsvariablen normalisieren, um sicherzustellen, dass Merkmale mit größeren Skalen nicht diejenigen mit kleineren Skalen dominieren.
Die Normalisierung ist in den folgenden Szenarien am effektivsten:
- Unbekannte oder nicht-gaußsche Verteilung: Wenn die Verteilung der Daten nicht bekannt ist oder nicht einem normalen (Gaußschen) Muster folgt. Bei einer linearen Regression kann es zum Beispiel sinnvoll sein, die abhängige Variable so zu normalisieren, dass sie eher einer Glockenkurve ähnelt, was das Vertrauen in unsere Schätzungen erhöht.
- Abstandsbasierte Algorithmen: Bei der Verwendung von Algorithmen für maschinelles Lernen, die auf Abständen zwischen Datenpunkten basieren, wie z. B. k-Nächste Nachbarn (k-NN), ist eine Normalisierung erforderlich, um zu verhindern, dass Merkmale mit größeren Skalen die Abstandsberechnungen dominieren.
Was ist Normung?
Während bei der Normalisierung die Merkmale auf einen bestimmten Bereich skaliert werden, werden bei der Standardisierung, die auch als z-Score-Skalierung bezeichnet wird, die Daten so umgewandelt, dass sie einen Mittelwert von 0 und eine Standardabweichung von 1 haben. Bei diesem Verfahren werden die Merkmalswerte angepasst, indem der Mittelwert subtrahiert und durch die Standardabweichung geteilt wird. Vielleicht hast du schon von der "Zentrierung und Skalierung" von Daten gehört. Nun, Standardisierung bedeutet dasselbe: erst zentrieren, dann skalieren.
Die Formel für die Normung lautet:
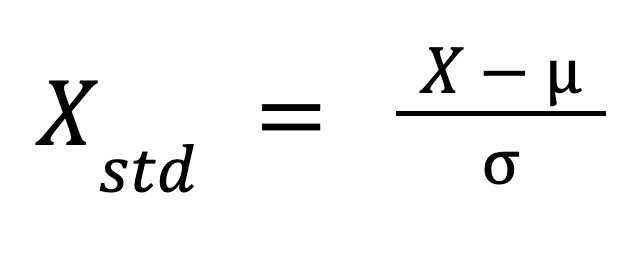
Wo:
- X ist der ursprüngliche Wert,
- mu ist der Mittelwert des Merkmals, und
- sigma ist die Standardabweichung des Merkmals.
Diese Formel skaliert die Daten so um, dass ihre Verteilung einen Mittelwert von 0 und eine Standardabweichung von 1 hat.
Wann solltest du Daten standardisieren?
Eine Standardisierung ist in den folgenden Fällen am sinnvollsten:
- Gradientenbasierte Algorithmen: Die Support Vector Machine (SVM) benötigt standardisierte Daten für eine optimale Leistung. Modelle wie die lineare Regression und die logistische Regression gehen zwar nicht von einer Standardisierung aus, können aber dennoch davon profitieren, vor allem wenn die Merkmale sehr unterschiedlich groß sind.
- Dimensionalitätsreduktion: Die Standardisierung erfolgt durch Techniken zur Dimensionalitätsreduzierung wie PCA, weil PCA die Richtung identifiziert, in der die Varianz der Daten maximiert wird. Die Normalisierung des Mittelwerts allein reicht nicht aus, da die PCA sowohl den Mittelwert als auch die Varianz berücksichtigt und unterschiedliche Merkmalskalen die Analyse verzerren würden.
Normalisierung vs. Standardisierung: Die wichtigsten Unterschiede
Manchmal ist es schwierig, zwischen Normalisierung und Standardisierung zu unterscheiden. Zum einen wird Normalisierung manchmal als allgemeiner Begriff verwendet, während Standardisierung eine etwas spezifischere oder speziell technische Bedeutung hat. Auch Datenanalysten und Datenwissenschaftler, die mit den Begriffen vertraut sind, haben vielleicht noch Schwierigkeiten, Anwendungsfälle zu unterscheiden.
Beides sind Skalierungstechniken, aber sie unterscheiden sich in ihren Ansätzen und Anwendungen. Diese Unterschiede zu verstehen, ist der Schlüssel zur Wahl der richtigen Technik für dein maschinelles Lernmodell.
Methoden zur Skalierung
Die Normalisierung skaliert die Merkmalswerte innerhalb eines vordefinierten Bereichs, oft zwischen 0 und 1. Dies ist besonders nützlich für Modelle, bei denen die Skala der Merkmale stark variiert. Im Gegensatz dazu zentriert die Standardisierung die Daten um den Mittelwert (0) und skaliert sie entsprechend der Standardabweichung (1).
Empfindlichkeit gegenüber Ausreißern
Die verschiedenen Normalisierungsverfahren unterscheiden sich in ihrer Effektivität bei der Behandlung von Ausreißern. Die Mittelwertnormalisierung kann in einigen Szenarien Ausreißer erfolgreich ausgleichen, aber andere Techniken sind möglicherweise nicht so effektiv. Im Allgemeinen können Normalisierungstechniken das Ausreißerproblem nicht so effektiv lösen wie die Standardisierung, da die Standardisierung ausdrücklich sowohl den Mittelwert als auch die Standardabweichung berücksichtigt.
Anwendungsfälle
Die Normalisierung wird häufig bei abstandsbasierten Algorithmen wie k-Nächste Nachbarn (k-NN) verwendet, bei denen die Merkmale auf der gleichen Skala liegen müssen, um die Genauigkeit der Abstandsberechnung zu gewährleisten. Die Standardisierung hingegen ist für gradientenbasierte Algorithmen wie Support Vector Machines (SVM) unerlässlich und wird häufig bei Verfahren zur Dimensionalitätsreduktion wie PCA angewendet, bei denen es wichtig ist, die korrekte Merkmalsvarianz beizubehalten.
Zusammenfassende Tabelle der Unterschiede
Betrachten wir all diese wichtigen Unterschiede in einer zusammenfassenden Tabelle, um den Vergleich zwischen Normalisierung und Standardisierung zu erleichtern:
| Kategorie | Normalisierung | Normung |
|---|---|---|
| Rescaling-Methode | Skaliert Daten auf der Grundlage von Minimal- und Maximalwerten in einem Bereich (normalerweise 0 bis 1). | Zentriert die Daten um den Mittelwert (0) und skaliert sie um die Standardabweichung (1). |
| Empfindlichkeit gegenüber Ausreißern | Die Normalisierung kann helfen, Ausreißer auszugleichen, wenn sie richtig eingesetzt wird, je nach Technik. | Die Standardisierung ist ein konsequenterer Ansatz zur Lösung von Ausreißerproblemen. |
| Gemeinsame Algorithmen | Wird oft in Algorithmen wie k-NN und neuronalen Netzen verwendet, die eine einheitliche Datengröße erfordern. | Am besten geeignet für Algorithmen, bei denen die Merkmale eine gemeinsame Skala haben müssen, wie z. B. logistische Regression, SVM und PCA. |
Visualisierung der Unterschiede
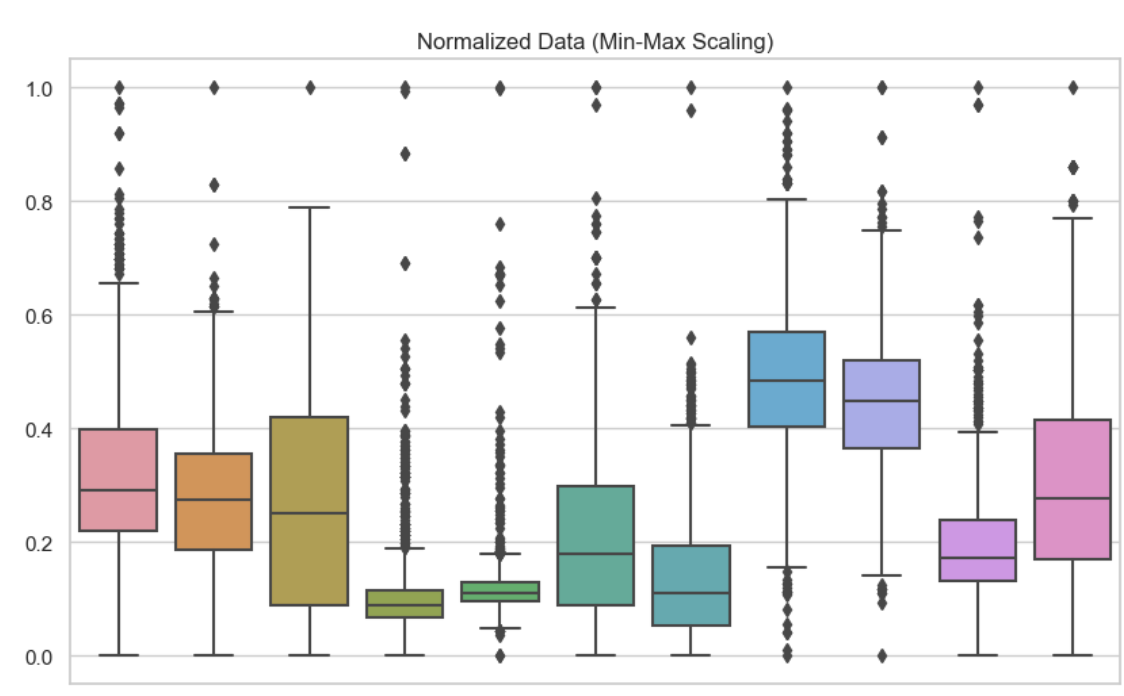
Um die Unterschiede zwischen Normalisierung und Standardisierung zu verstehen, ist es hilfreich, ihre Auswirkungen visuell und in Bezug auf die Modellleistung zu sehen. Hier habe ich Boxplots eingefügt, um diese verschiedenen Skalierungstechniken zu zeigen. Hier habe ich die Min-Max-Normalisierung für jede der Variablen in meinem Datensatz verwendet. Wir können sehen, dass kein Wert kleiner als 0 oder größer als 1 ist.
Normalisierte Daten. Bild vom Autor
In dieser zweiten Visualisierung habe ich jede der Variablen standardisiert. Wir können sehen, dass die Daten bei Null zentriert sind.
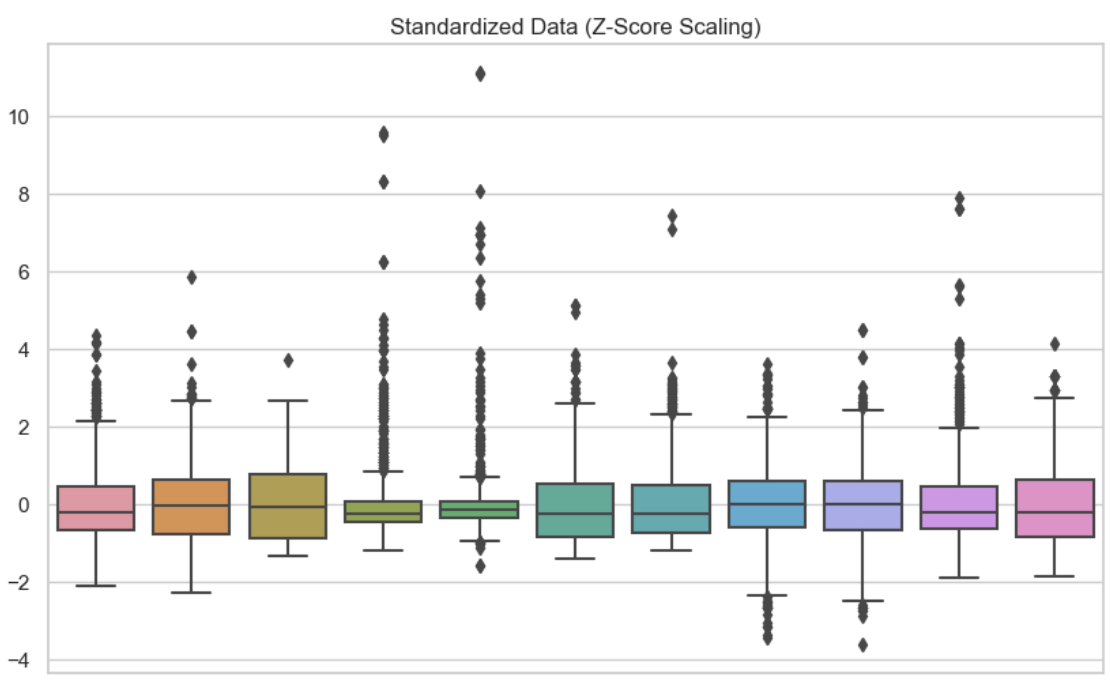 Standardisierte Daten. Bild vom Autor
Standardisierte Daten. Bild vom Autor
Vorteile und Nachteile
Zu den Vorteilen gehören eine verbesserte Modellleistung und ausgewogene Merkmalsbeiträge. Die Normalisierung kann jedoch die Interpretierbarkeit aufgrund der festen Skala einschränken, während die Standardisierung die Interpretation ebenfalls erschweren kann, da die Werte nicht mehr ihre ursprünglichen Einheiten widerspiegeln. Es gibt immer einen Kompromiss zwischen Modellkomplexität und Modellgenauigkeit.
Normalisierung und Standardisierung in der linearen Regression
Betrachten wir, wie die Normalisierung (in diesem Fall die Mittelwertnormalisierung) und die Standardisierung die Interpretation eines einfachen linearen Regressionsmodells verändern können. Das R-Quadrat oder das bereinigte R-Quadrat wäre für jedes Modell gleich, also geht es bei der Merkmals-Skalierung hier nur um die Interpretation unseres Modells.
| Transformation angewandt | Unabhängige Variable (Hausgröße) | Abhängige Variable (Hauspreis) | Interpretation |
|---|---|---|---|
| Mittelwert-Normalisierung | Mittelwert Normalisiert | Original | Du prognostizierst den ursprünglichen Hauspreis für jede Veränderung der Hausgröße im Verhältnis zum Durchschnitt. |
| Normung | Standardisiert | Original | Du sagst den ursprünglichen Hauspreis für jede Veränderung der Hausgröße um eine Standardabweichung voraus. |
| Mittelwert-Normalisierung | Original | Mittelwert Normalisiert | Du sagst den Hauspreis relativ zum Durchschnitt für jede Erhöhung der ursprünglichen Hausgröße um eine Einheit voraus. |
| Normung | Original | Standardisiert | Du sagst den standardisierten Hauspreis für jede Erhöhung der ursprünglichen Hausgröße um eine Einheit voraus. |
| Normalisierung des Mittelwerts (beide Variablen) | Mittelwert Normalisiert | Mittelwert Normalisiert | Du sagst den Hauspreis relativ zum Durchschnitt für jede Veränderung der Hausgröße relativ zum Durchschnitt voraus. |
| Standardisierung (beide Variablen) | Standardisiert | Standardisiert | Du sagst den standardisierten Hauspreis für jede Veränderung der Hausgröße um eine Standardabweichung voraus. |
Ein weiterer wichtiger Hinweis: Wenn du bei der linearen Regression die unabhängigen und abhängigen Variablen standardisierst, bleibt das r-Quadrat gleich. Das liegt daran, dass r-Quadrat den Anteil der Varianz in y misst, der durch x erklärt wird, und dieser Anteil bleibt gleich, egal ob die Variablen standardisiert sind oder nicht. Die Standardisierung der abhängigen Variable wird jedoch den RMSE verändern, da der RMSE in denselben Einheiten gemessen wird wie die abhängige Variable. Da y nun standardisiert ist, wird der RMSE nach der Standardisierung niedriger sein. Genauer gesagt, spiegelt er den Fehler in Form der Standardabweichung der standardisierten Variablen wider, nicht in den ursprünglichen Einheiten. Wenn dich die Regression besonders interessiert, solltest du unseren Kurs Einführung in die Regression mit Statistikmodellen in Python besuchen, um ein Experte zu werden.
Fazit
Die Skalierung von Merkmalen, zu der auch die Normalisierung und Standardisierung gehört, ist ein wichtiger Bestandteil der Datenvorverarbeitung beim maschinellen Lernen. Wenn du die richtigen Zusammenhänge für die Anwendung der einzelnen Techniken kennst, kannst du die Leistung und Genauigkeit deiner Modelle erheblich verbessern.
Wenn du dein Wissen über die Skalierung von Merkmalen und ihre Rolle beim maschinellen Lernen erweitern und vertiefen möchtest, haben wir auf dem DataCamp einige hervorragende Ressourcen, die dir den Einstieg erleichtern können. In unserem Artikel über Normalisierung im maschinellen Lernen findest du grundlegende Konzepte, oder du kannst unseren Kurs End-to-End Machine Learning besuchen, der sich mit realen Anwendungen beschäftigt.
Werde ein ML-Wissenschaftler
Erfahrene Datenexpertin und Autorin, die sich leidenschaftlich dafür einsetzt, aufstrebende Datenexperten zu fördern.