Euclidean distance, a concept that traces its roots back to ancient Greek mathematics, has become an essential tool in modern data science, machine learning, and spatial analysis. Named after the famous Euclid, this metric provides a fundamental way to measure the straight-line distance between points in space, whether in two dimensions or many more.
What is Euclidean Distance?
Euclidean distance represents the shortest path between two points in Euclidean space. It's the distance you would measure with a ruler, extended to any number of dimensions. This concept is deeply rooted in the Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse equals the sum of squares of the other two sides.

“Philosopher teaching Euclidean distance.” Image by Dall-E
The Euclidean Distance Formula
Let's break down the Euclidean distance formula for different dimensions:
2D Euclidean distance
In a two-dimensional plane, the Euclidean distance between points A(x₁, y₁) and B(x₂, y₂) is given by:
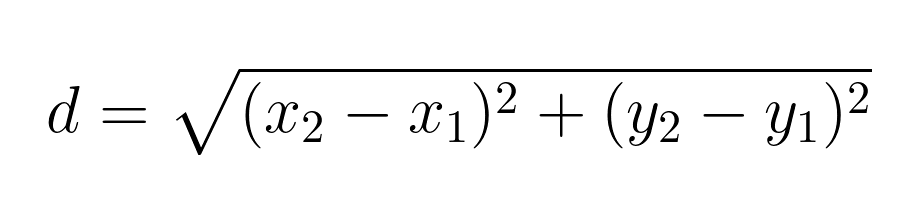
For example, let's calculate the distance between points A(1, 2) and B(4, 6):
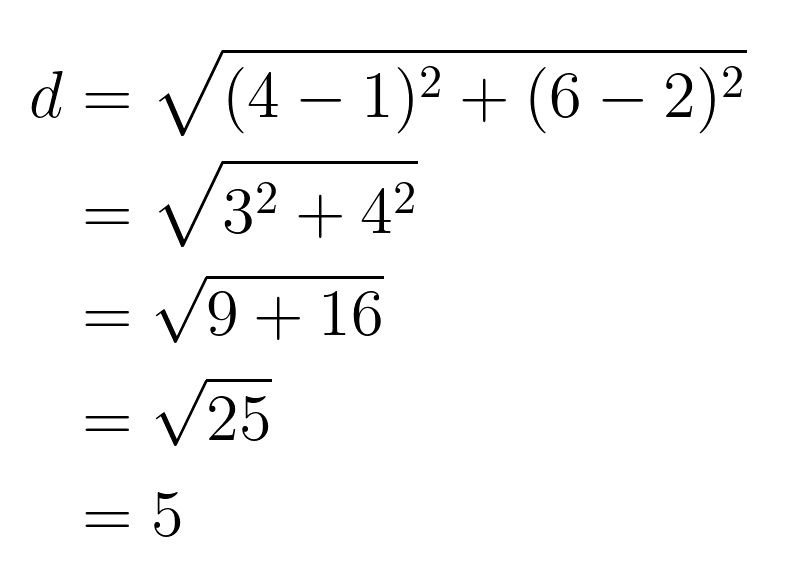
2D Euclidean distance visualization
To better understand 2D Euclidean distance, let's visualize it:
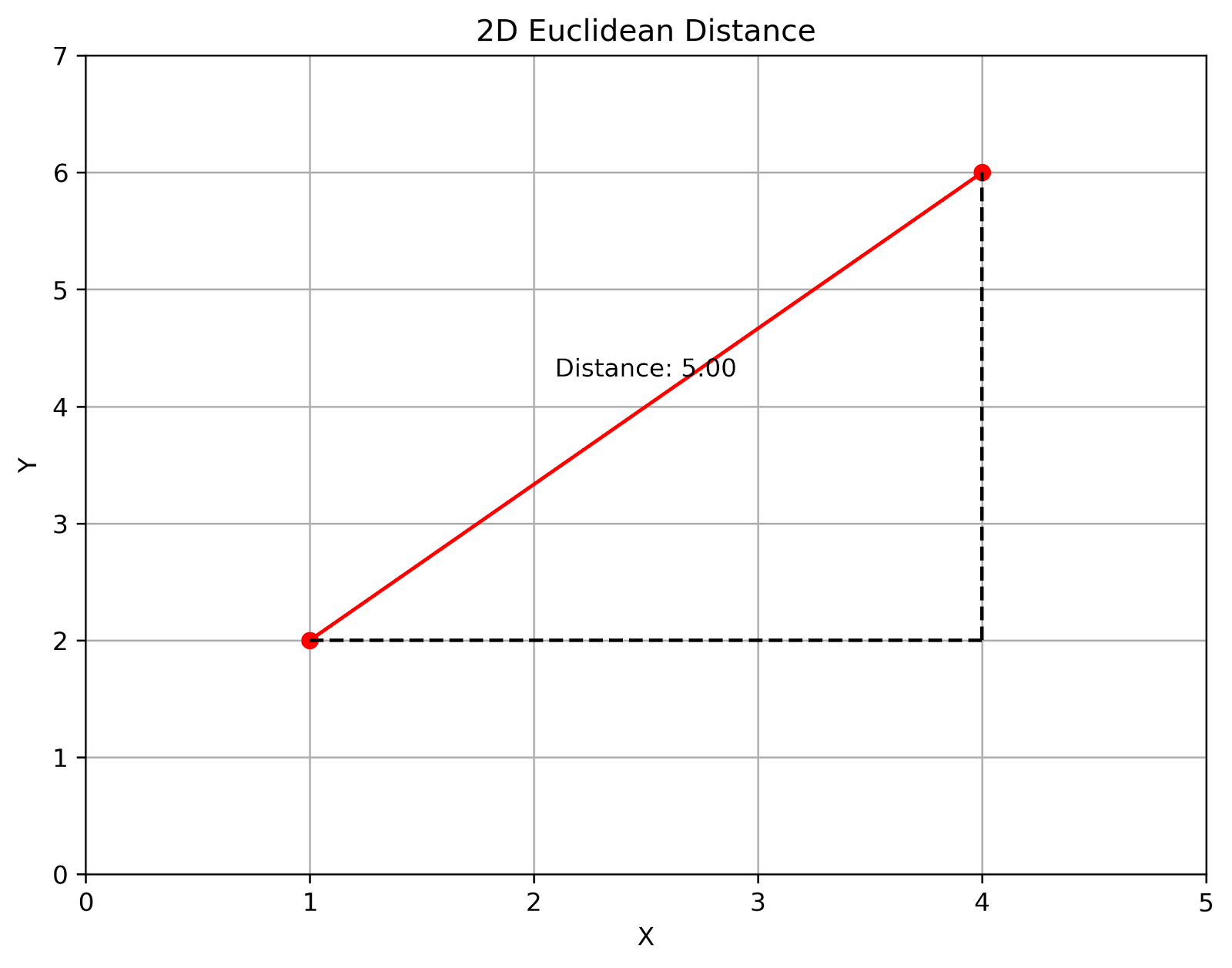
2D Euclidean distance. Image by Author
This visualization shows the Euclidean distance between two points in a 2D plane. The red line represents the direct distance, while the dashed lines form a right triangle, illustrating the Pythagorean theorem in action.
3D Euclidean distance
Extending to three dimensions, for points A(x₁, y₁, z₁) and B(x₂, y₂, z₂), the formula becomes:
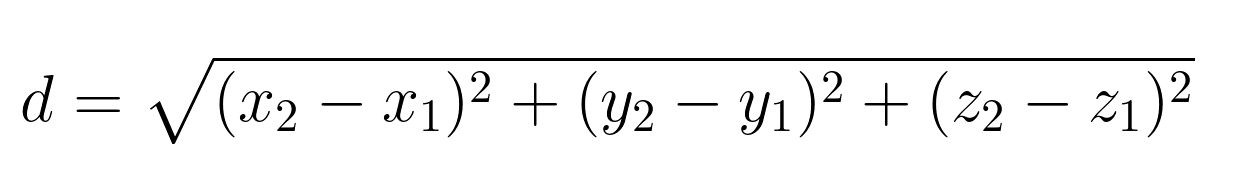
3D Euclidean distance visualization
Let's visualize the 3D Euclidean distance:
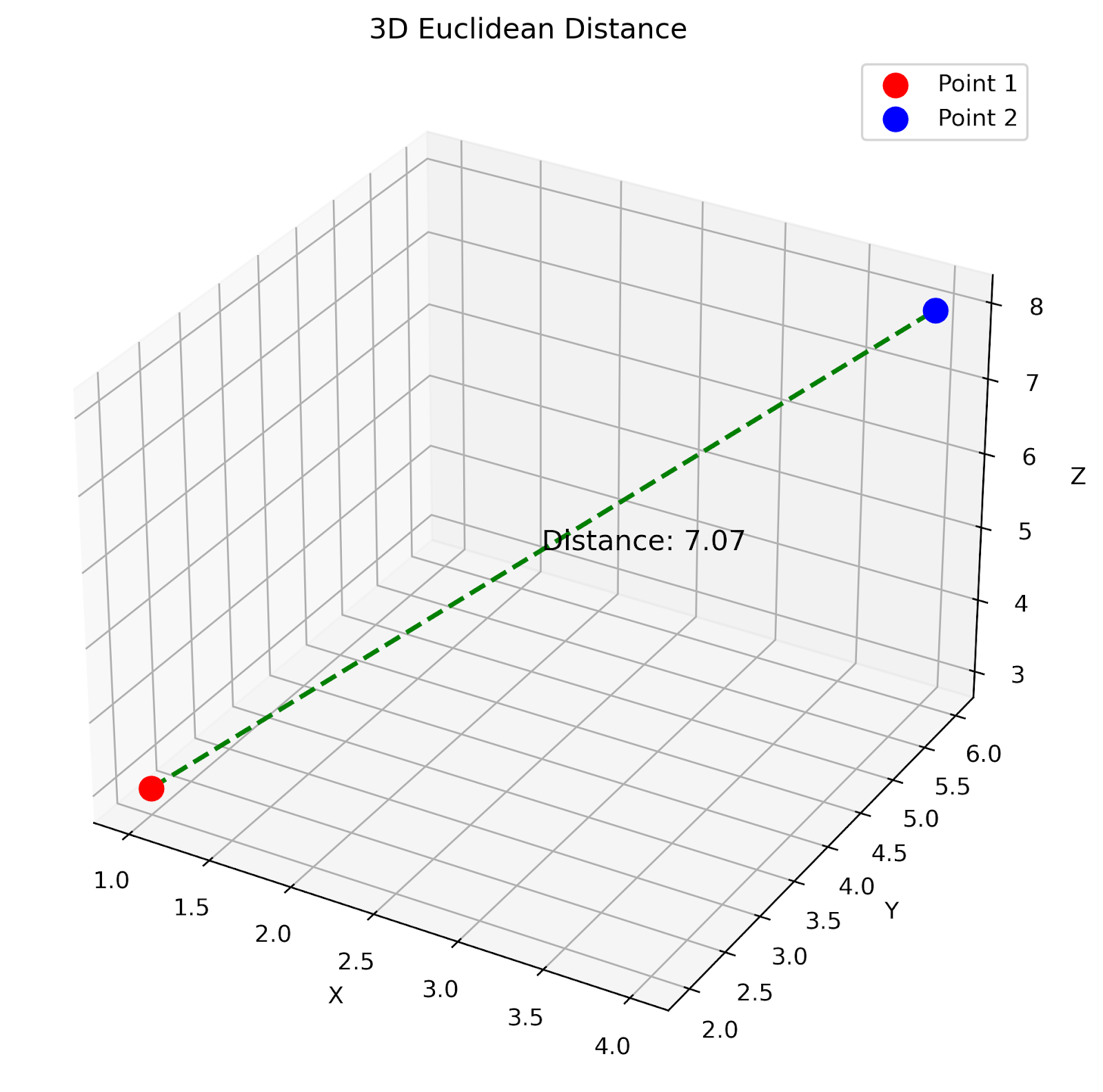
3D Euclidean distance. Image by Author
This 3D plot shows the Euclidean distance between two points in three-dimensional space. The green dashed line represents the direct distance between the points.
N-dimensional Euclidean distance
In a space with n dimensions, the Euclidean distance between points A(a₁, a₂, ..., aₙ) and B(b₁, b₂, ..., bₙ) is:
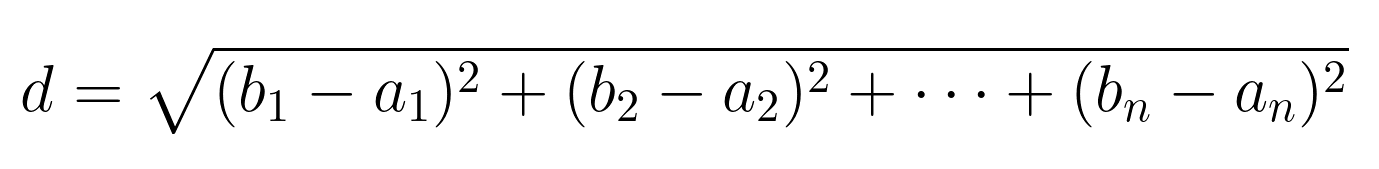
This can be more concisely written using summation notation:
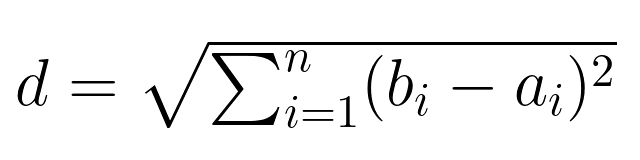
Relationship to Linear Algebra Concepts
Understanding Euclidean distance goes beyond just knowing how to measure the shortest path between two points. It's also about seeing these distances through the lens of linear algebra, a field that helps us describe and solve problems about space and dimensions using vectors and their properties. For more insights into this subject, explore the Linear Algebra for Data Science in R course, which covers these concepts comprehensively.
Euclidean distance as a vector norm
Euclidean distance measures how far apart two points are in space. Imagine you have two points, one at the start of a hiking trail and another at the top of a hill. The straight-line path you'd walk from the start to the top can be thought of as the Euclidean distance. In linear algebra, this is like finding the length of an arrow (or vector) that points straight from the beginning of the trail (point A) to the top of the hill (point B). This length is called the vector's "norm," and it's just a fancy term for the length of this straight-line path.
Dot product and the cosine of the angle
When dealing with directions, the dot product helps us understand the angle between any two arrows. For instance, if you're at the intersection of two roads, the dot product would tell you how much one road points toward the other. This is calculated using the lengths of each road (like the norms we talked about) and the angle between them. The closer this value is to 0, the more the roads approach being perpendicular to each other. When you relate this to distance, the formula for the dot product helps break down the Euclidean distance into components that are easier to manage, showing how changes in direction affect the overall distance.
Euclidean distance and vector subtraction
To find the Euclidean distance between two points using vectors, you essentially subtract one point from another to create a new vector. This new vector points directly from one point to the other and its length is the Euclidean distance you're interested in. It's like plotting a direct route on a map from your house to the nearest grocery store by subtracting their coordinates; this gives you a straight line (or vector) that shows the shortest path you can take.
Calculating Euclidean Distance in Python and R
Let's explore implementations of Euclidean distance calculations using both Python and R. We'll examine how to create custom functions and utilize built-in libraries to enhance efficiency.
Python example
In Python, we can leverage the power of NumPy for efficient array operations and SciPy for specialized distance calculations. Here's how we can implement Euclidean distance:
import numpy as np
from scipy.spatial.distance import euclidean
def euclidean_distance(point1, point2):
return np.sqrt(np.sum((np.array(point1) - np.array(point2))**2))
# 2D example
point_a = (1, 2)
point_b = (4, 6)
distance_2d = euclidean_distance(point_a, point_b)
print(f"2D Euclidean distance: {distance_2d:.2f}")
# 3D example
point_c = (1, 2, 3)
point_d = (4, 6, 8)
distance_3d = euclidean_distance(point_c, point_d)
print(f"3D Euclidean distance: {distance_3d:.2f}")
# Using SciPy for efficiency
distance_scipy = euclidean(point_c, point_d)
print(f"3D Euclidean distance (SciPy): {distance_scipy:.2f}")When we run this code, we expect to see output similar to:
2D Euclidean distance: 5.00
3D Euclidean distance: 7.07
3D Euclidean distance (SciPy): 7.07The SciPy function is generally faster and more optimized, especially for high-dimensional data, but our custom function helps illustrate the underlying calculation.
Become a ML Scientist
R example
R provides several ways to calculate Euclidean distance. We'll create a custom function and compare it with the dist() function from the stats library.
euclidean_distance <- function(point1, point2) {
sqrt(sum((point1 - point2)^2))
}
# 2D example
point_a <- c(1, 2)
point_b <- c(4, 6)
distance_2d <- euclidean_distance(point_a, point_b)
print(paste("2D Euclidean distance:", round(distance_2d, 2)))
# 3D example
point_c <- c(1, 2, 3)
point_d <- c(4, 6, 8)
distance_3d <- euclidean_distance(point_c, point_d)
print(paste("3D Euclidean distance:", round(distance_3d, 2)))
# Using the dist() function from stats
distance_builtin <- stats::dist(rbind(point_c, point_d), method = "euclidean")
print(paste("3D Euclidean distance (built-in):", round(as.numeric(distance_builtin), 2)))Running this R code should produce output like:
[1] "2D Euclidean distance: 5"
[1] "3D Euclidean distance: 7.07"
[1] "3D Euclidean distance (built-in): 7.07"Our custom euclidean_distance function uses R's vectorized operations, making it concise and efficient. The dist() function from stats returns the same result, validating our custom function. Both methods return a matrix.
Applications of Euclidean Distance
Euclidean distance is a straightforward way to measure how far apart things are. It’s used in various areas to handle problems involving space and distance.
K-nearest neighbors (KNN)
In the k-nearest neighbors algorithm, Euclidean distance helps find the nearest neighbors to a point. This helps decide how to classify new data—like deciding if an email is spam based on what similar emails look like, or recommending products that are similar to what a customer already likes.
K-means clustering
In k-means clustering, Euclidean distance helps sort data points into groups by connecting each point to the nearest center of a cluster. This helps in organizing data into categories that share similarities, useful in customer segmentation or during research to group similar subjects together.
Multidimensional scaling (MDS)
Multidimensional scaling uses Euclidean distance to simplify complex data into something easier to visualize and understand. It takes data that usually has many details (dimensions) and reduces it so that it’s simpler to look at and analyze, helping to spot trends and patterns more clearly.
Image processing
In tasks like detecting edges in images or recognizing objects, Euclidean distance measures how much pixel colors change, which helps in outlining objects or identifying important features in an image. This is helpful in things like medical imaging to identify diseases, or in security systems to recognize faces or objects.
Robotics
For robots, like drones or self-driving cars, Euclidean distance helps calculate the simplest route from one point to another. This helps robots and other automated systems move efficiently and safely, avoiding obstacles and calculating the easiest paths to their destinations.
Comparison with Other Distance Metrics
Euclidean distance is one of many ways to measure how far apart points are, but different situations call for different methods. Here’s how it stacks up against other common distance metrics:
Manhattan distance
Also known as "city block" distance, Manhattan distance measures the total sum of the absolute differences along each dimension. Imagine you're walking through a city's grid-like streets; the distance you'd travel block by block is your Manhattan distance. This method is particularly handy in environments that mimic a grid, like navigating city streets or in some types of games. It's also useful when you’re dealing with very high-dimensional data, where Euclidean distance can become less reliable. To explore more, check out our tutorial on Manhattan distance.
Cosine distance
Cosine distance looks at the angle between two points or vectors. Instead of focusing on how long the line is between them, it considers how they are oriented relative to each other. This makes it especially useful in fields like text analysis or recommendation systems, where the direction of the data (like word counts in articles or user preferences) matters more than the magnitude (how much). For a deeper understanding, see our article on cosine distance.
Chebyshev distance
Chebyshev distance is another way to measure distance, focusing on the greatest difference along any dimension. It’s like playing chess: the king moves to the square that is the farthest away in the minimum number of moves, irrespective of whether it's horizontal, vertical, or diagonal. This metric is particularly useful in scenarios where you need to consider only the most significant of multiple differences. Learn more by reading our tutorial on Chebyshev distance.
Limitations of Euclidean Distance
While Euclidean distance is widely used due to its intuitive nature and straightforward calculation, it does have some notable limitations. Understanding these can help in choosing the right distance measure or in adjusting the data to mitigate these issues.
Scale sensitivity
Euclidean distance can be disproportionately affected by the scale of the features. For instance, in a dataset containing income and age, income typically spans a much larger range (perhaps thousands or tens of thousands) compared to age (usually ranging just up to about 100). This disparity can lead to income overwhelming the distance calculation, skewing results towards its scale.
Mitigation: Normalizing or standardizing the data can help balance the scales of different features, ensuring that no single feature unduly influences the distance calculation.
Curse of dimensionality
The curse of dimensionality refers to various phenomena that emerge as the number of dimensions in a dataset increases. One of these is that the concept of 'proximity' or 'distance' becomes less meaningful—distances tend to converge, making it hard to distinguish between near and far points effectively.
Mitigation: Techniques like principal component analysis (PCA) or t-distributed stochastic neighbor embedding (t-SNE) reduce the dimensionality of the data. These methods help by distilling the essential features with the most variance, which can help to simplify the data.
Outlier sensitivity
Euclidean distance calculations can also be heavily influenced by outliers. In high-dimensional spaces, a single outlier can drastically alter distances, making some data points appear far more similar or different than they truly are.
In fact, the sensitivity of linear regression to outliers is related to the concept of Euclidean distance. This is because, in linear regression, the model minimizes the sum of squared residuals, which are the differences between observed and predicted values. Doing this essentially measures the Euclidean distance between the observed data points and the regression line. Outliers can disproportionately affect this distance because the square of larger deviations increases more rapidly than smaller ones.
Mitigation: Using more robust metrics that are less sensitive to outliers can help, such as the Manhattan distance for certain types of data. Additionally, preprocessing data to identify and treat outliers—either by adjusting them or removing them—can prevent them from skewing the distance calculations.
Alternative Approach: Considering weighted Euclidean distance is another strategy. This variation of Euclidean distance assigns different weights to different dimensions or features, potentially down-weighting those prone to outliers or noise.
Conclusion
As we've explored, Euclidean distance is a fundamental metric in many analytical and technological fields, providing a straightforward way to measure the straight-line distance between points. Understanding and utilizing Euclidean distance can enhance the accuracy and effectiveness of many applications, from machine learning algorithms to spatial analysis.
I encourage you to experiment with Euclidean distance in your projects and explore further learning opportunities through courses like Designing Machine Learning Workflows in Python and the Anomaly Detection in Python Course.
Become an ML Scientist
As an adept professional in Data Science, Machine Learning, and Generative AI, Vinod dedicates himself to sharing knowledge and empowering aspiring data scientists to succeed in this dynamic field.
Euclidean Distance FAQs
Why is Euclidean distance important in machine learning?
Euclidean distance helps in various machine learning algorithms by quantifying how similar or different data points are, which is important for tasks like classification, clustering, and anomaly detection.
Is Euclidean distance always the best choice for measuring distances in data science?
Not always. The best distance metric depends on the data type and the specific problem. For example, Manhattan distance might be more appropriate for high-dimensional data or situations where grid-like movement is more representative.
How does Euclidean distance handle negative coordinates?
Euclidean distance measures the absolute difference between corresponding coordinates, treating all coordinates equally, whether they are positive or negative.
Can Euclidean distance be used with categorical data?
No, Euclidean distance generally requires numerical input to calculate distances. Alternative methods like Hamming distance or other custom similarity measures are used for categorical data.
How does the choice of Euclidean distance impact the performance of clustering algorithms like k-means?
Using Euclidean distance in clustering algorithms such as K-means directly influences how clusters are formed, as it determines the geometric properties of these clusters. Euclidean distance tends to form spherical clusters, where the mean serves as the cluster center. This can impact the clustering performance, particularly when the natural clusters in the data are not spherical.




