A distância euclidiana, um conceito que tem suas raízes na matemática grega antiga, tornou-se uma ferramenta essencial na ciência de dados moderna, no aprendizado de máquina e na análise espacial. Batizada com o nome do famoso Euclides, essa métrica fornece uma maneira fundamental de medir a distância em linha reta entre pontos no espaço, seja em duas dimensões ou em muitas outras.
O que é distância euclidiana?
A distância euclidiana representa o caminho mais curto entre dois pontos no espaço euclidiano. É a distância que você mediria com uma régua, ampliada para qualquer número de dimensões. Esse conceito está profundamente enraizado no teorema de Pitágoras, que afirma que, em um triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos outros dois lados.

"Filósofo ensinando a distância euclidiana." Imagem de Dall-E
A fórmula da distância euclidiana
Vamos detalhar a fórmula da distância euclidiana para diferentes dimensões:
Distância euclidiana 2D
Em um plano bidimensional, a distância euclidiana entre os pontos A(x₁, y₁) e B(x₂, y₂) é dada por:
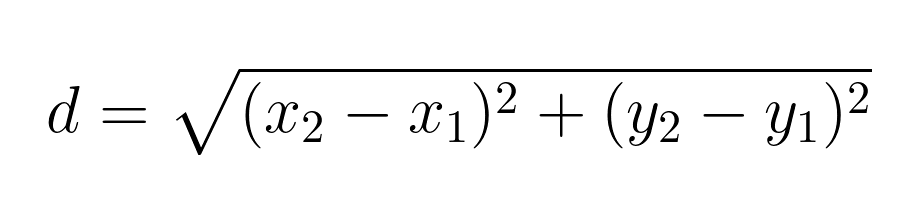
Por exemplo, vamos calcular a distância entre os pontos A(1, 2) e B(4, 6):
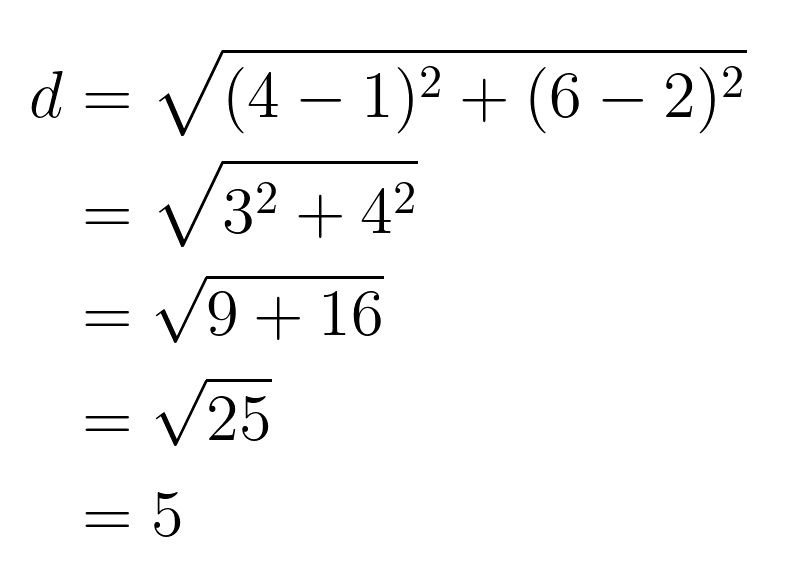
Visualização da distância euclidiana 2D
Para que você entenda melhor a distância euclidiana 2D, vamos visualizá-la:
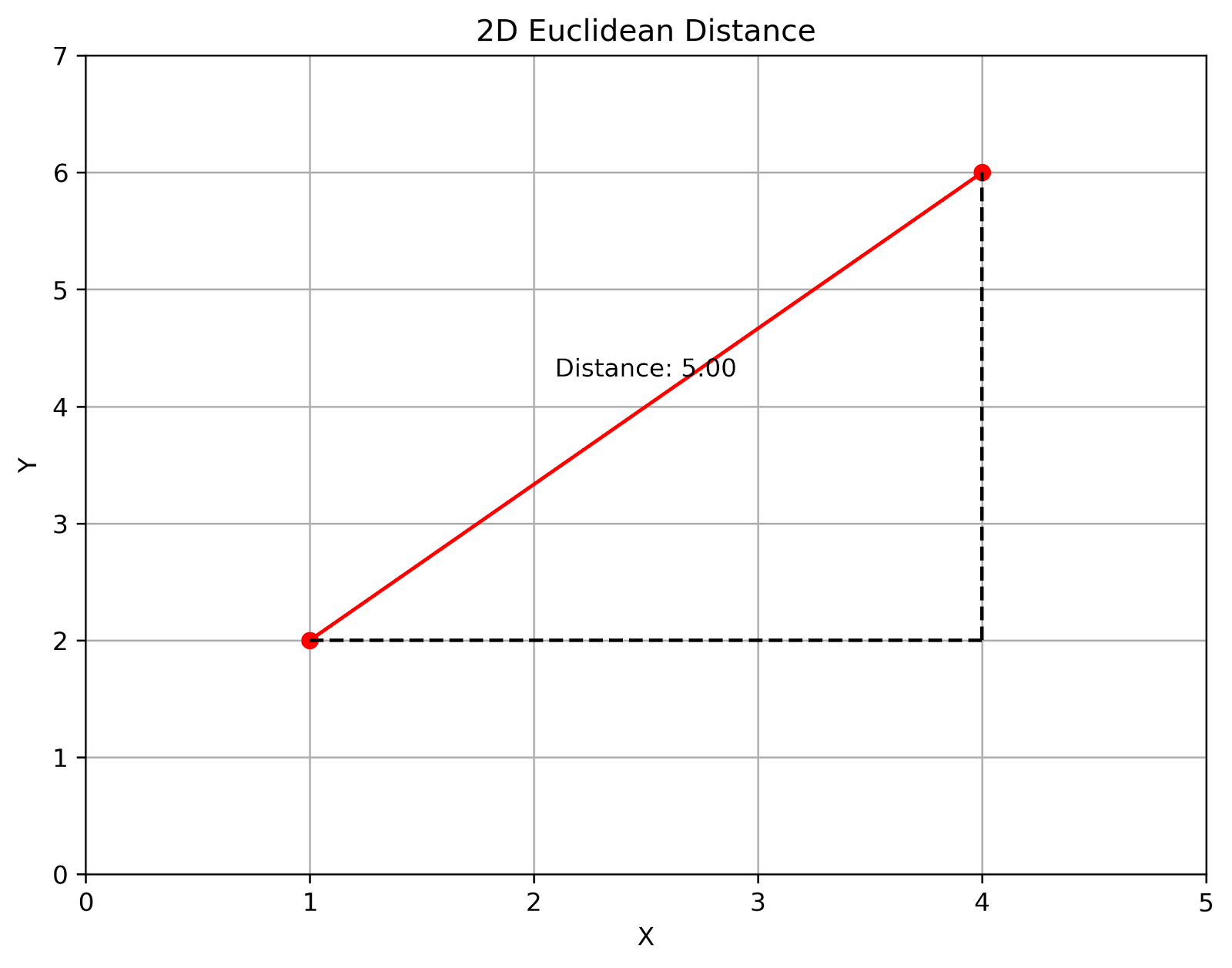
Distância euclidiana 2D. Imagem do autor
Essa visualização mostra a distância euclidiana entre dois pontos em um plano 2D. A linha vermelha representa a distância direta, enquanto as linhas tracejadas formam um triângulo retângulo, ilustrando o teorema de Pitágoras em ação.
Distância euclidiana 3D
Estendendo para três dimensões, para os pontos A(x₁, y₁, z₁) e B(x₂, y₂, z₂), a fórmula se torna:
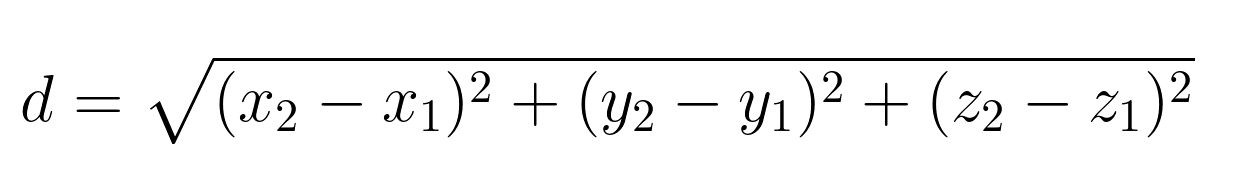
Visualização da distância euclidiana em 3D
Vamos visualizar a distância euclidiana em 3D:
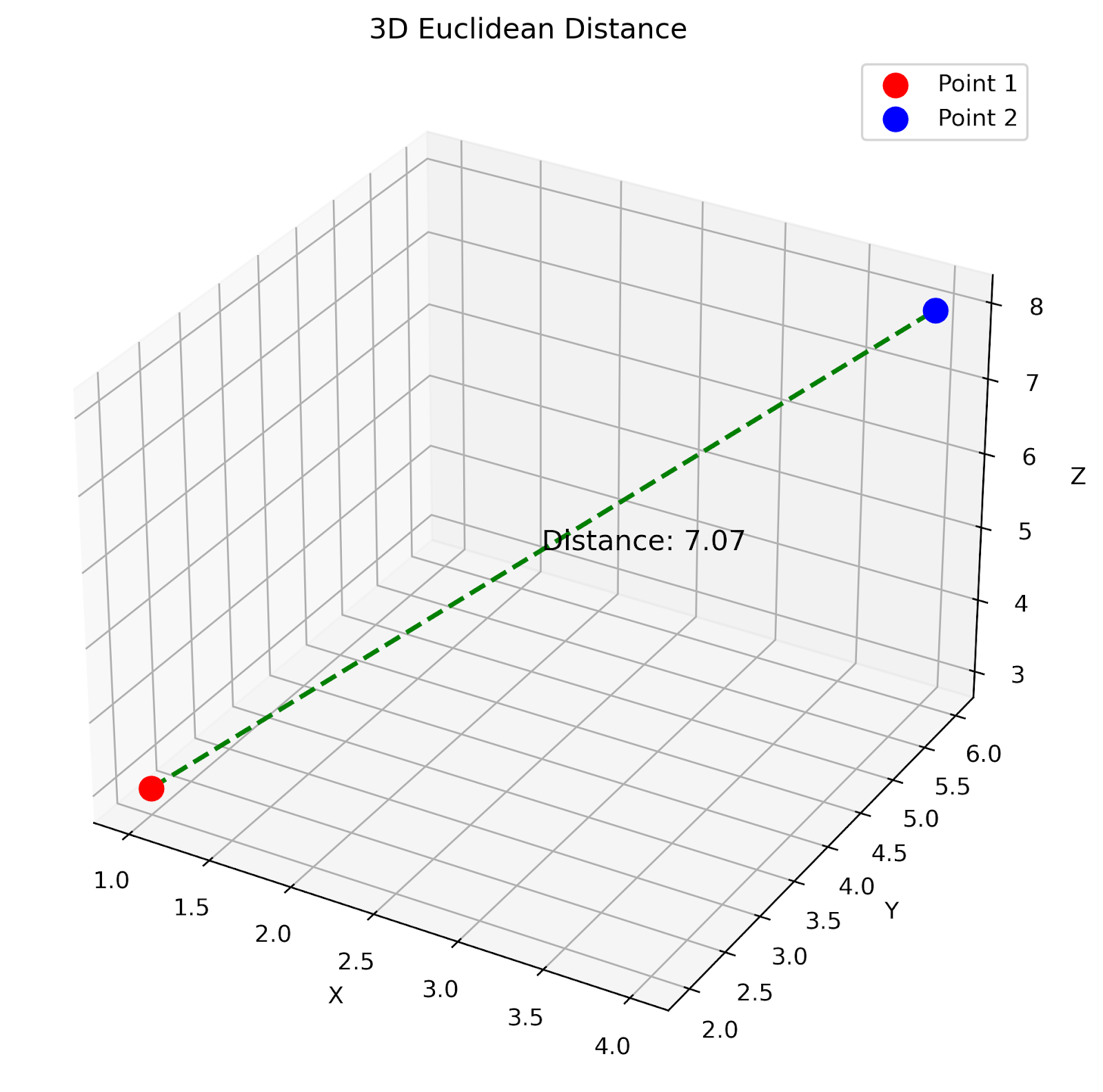
Distância euclidiana 3D. Imagem do autor
Esse gráfico 3D mostra a distância euclidiana entre dois pontos no espaço tridimensional. A linha tracejada verde representa a distância direta entre os pontos.
Distância Euclidiana N-dimensional
Em um espaço com n dimensões, a distância euclidiana entre os pontos A(a₁, a₂, ..., aₙ) e B(b₁, b₂, ..., bₙ) é:
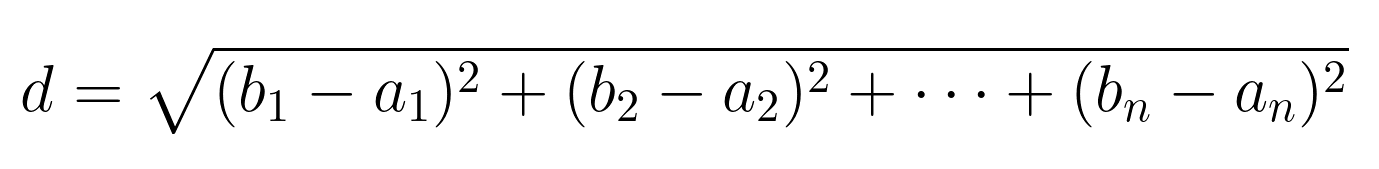
Isso pode ser escrito de forma mais concisa usando a notação de soma:
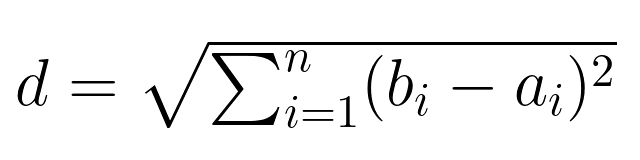
Relação com conceitos de álgebra linear
Entender a distância euclidiana vai além de apenas saber como medir o caminho mais curto entre dois pontos. Trata-se também de ver essas distâncias pelas lentes da álgebra linear, um campo que nos ajuda a descrever e resolver problemas sobre espaço e dimensões usando vetores e suas propriedades. Para obter mais informações sobre esse assunto, explore o curso Linear Algebra for Data Science in R, que aborda esses conceitos de forma abrangente.
Distância euclidiana como norma vetorial
A distância euclidiana mede a distância entre dois pontos no espaço. Imagine que você tem dois pontos, um no início de uma trilha de caminhada e outro no topo de uma colina. O caminho em linha reta que você percorreria desde o início até o topo pode ser considerado como a distância euclidiana. Em álgebra linear, isso é como encontrar o comprimento de uma seta (ou vetor) que aponta diretamente do início da trilha (ponto A) para o topo da colina (ponto B). Esse comprimento é chamado de "norma" do vetor e é apenas um termo sofisticado para o comprimento desse caminho em linha reta.
O produto escalar e o cosseno do ângulo
Ao lidar com direções, o produto escalar nos ajuda a entender o ângulo entre duas setas quaisquer. Por exemplo, se você estiver na interseção de duas estradas, o produto de pontos lhe dirá o quanto uma estrada aponta para a outra. Isso é calculado usando os comprimentos de cada estrada (como as normas de que falamos) e o ângulo entre elas. Quanto mais próximo esse valor estiver de 0, mais as estradas se aproximam de serem perpendiculares umas às outras. Quando você relaciona isso à distância, a fórmula do produto escalar ajuda a dividir a distância euclidiana em componentes que são mais fáceis de gerenciar, mostrando como as mudanças de direção afetam a distância total.
Distância euclidiana e subtração de vetores
Para encontrar a distância euclidiana entre dois pontos usando vetores, você basicamente subtrai um ponto do outro para criar um novo vetor. Esse novo vetor aponta diretamente de um ponto para o outro e seu comprimento é a distância euclidiana na qual você está interessado. É como traçar uma rota direta em um mapa da sua casa até o supermercado mais próximo subtraindo suas coordenadas; isso lhe dá uma linha reta (ou vetor) que mostra o caminho mais curto que você pode seguir.
Cálculo da distância euclidiana em Python e R
Vamos explorar implementações de cálculos de distância euclidiana usando Python e R. Examinaremos como criar funções personalizadas e utilizar bibliotecas internas para aumentar a eficiência.
Exemplo de Python
No Python, podemos aproveitar o poder do NumPy para operações de matriz eficientes e do SciPy para cálculos de distância especializados. Veja como podemos implementar a distância euclidiana:
import numpy as np
from scipy.spatial.distance import euclidean
def euclidean_distance(point1, point2):
return np.sqrt(np.sum((np.array(point1) - np.array(point2))**2))
# 2D example
point_a = (1, 2)
point_b = (4, 6)
distance_2d = euclidean_distance(point_a, point_b)
print(f"2D Euclidean distance: {distance_2d:.2f}")
# 3D example
point_c = (1, 2, 3)
point_d = (4, 6, 8)
distance_3d = euclidean_distance(point_c, point_d)
print(f"3D Euclidean distance: {distance_3d:.2f}")
# Using SciPy for efficiency
distance_scipy = euclidean(point_c, point_d)
print(f"3D Euclidean distance (SciPy): {distance_scipy:.2f}")Quando executamos esse código, esperamos ver um resultado semelhante a:
2D Euclidean distance: 5.00
3D Euclidean distance: 7.07
3D Euclidean distance (SciPy): 7.07Em geral, a função SciPy é mais rápida e otimizada, especialmente para dados de alta dimensão, mas nossa função personalizada ajuda a ilustrar o cálculo subjacente.
Torne-se um cientista de ML
Exemplo de R
O R oferece várias maneiras de calcular a distância euclidiana. Criaremos uma função personalizada e a compararemos com a função a função dist() da biblioteca stats.
euclidean_distance <- function(point1, point2) {
sqrt(sum((point1 - point2)^2))
}
# 2D example
point_a <- c(1, 2)
point_b <- c(4, 6)
distance_2d <- euclidean_distance(point_a, point_b)
print(paste("2D Euclidean distance:", round(distance_2d, 2)))
# 3D example
point_c <- c(1, 2, 3)
point_d <- c(4, 6, 8)
distance_3d <- euclidean_distance(point_c, point_d)
print(paste("3D Euclidean distance:", round(distance_3d, 2)))
# Using the dist() function from stats
distance_builtin <- stats::dist(rbind(point_c, point_d), method = "euclidean")
print(paste("3D Euclidean distance (built-in):", round(as.numeric(distance_builtin), 2)))A execução desse código R deve produzir resultados como:
[1] "2D Euclidean distance: 5"
[1] "3D Euclidean distance: 7.07"
[1] "3D Euclidean distance (built-in): 7.07"Nossa função personalizada euclidean_distance usa as operações vetoriais do R, tornando-a concisa e eficiente. A função dist() de stats retorna o mesmo resultado, validando nossa função personalizada. Ambos os métodos retornam uma matriz.
Aplicações da distância euclidiana
A distância euclidiana é uma maneira simples de medir a distância entre as coisas. Ele é usado em várias áreas para lidar com problemas que envolvem espaço e distância.
K-nearest neighbors (KNN)
No algoritmo k-nearest neighbors, a distância euclidiana ajuda a encontrar os vizinhos mais próximos de um ponto. Isso ajuda a decidir como classificar novos dados, como decidir se um e-mail é spam com base na aparência de e-mails semelhantes ou recomendar produtos semelhantes aos que um cliente já gosta.
Agrupamento K-means
No k-means clustering, a distância euclidiana ajuda a classificar os pontos de dados em grupos, conectando cada ponto ao centro mais próximo de um cluster. Isso ajuda a organizar os dados em categorias que compartilham semelhanças, o que é útil na segmentação de clientes ou durante pesquisas para agrupar assuntos semelhantes.
Escala multidimensional (MDS)
O escalonamento multidimensional usa a distância euclidiana para simplificar dados complexos em algo mais fácil de visualizar e entender. Ele pega dados que normalmente têm muitos detalhes (dimensões) e os reduz para que sejam mais simples de ver e analisar, ajudando a identificar tendências e padrões com mais clareza.
Processamento de imagens
Em tarefas como a detecção de bordas em imagens ou o reconhecimento de objetos, a distância euclidiana mede o quanto as cores dos pixels mudam, o que ajuda a delinear objetos ou identificar recursos importantes em uma imagem. Isso é útil em coisas como imagens médicas para identificar doenças ou em sistemas de segurança para reconhecer rostos ou objetos.
Robótica
Para robôs, como drones ou carros autônomos, a distância euclidiana ajuda a calcular a rota mais simples de um ponto a outro. Isso ajuda os robôs e outros sistemas automatizados a se movimentarem com eficiência e segurança, evitando obstáculos e calculando os caminhos mais fáceis para seus destinos.
Comparação com outras métricas de distância
A distância euclidiana é uma das muitas maneiras de medir a distância entre os pontos, mas situações diferentes exigem métodos diferentes. Veja como ele se compara a outras métricas de distância comuns:
Distância de Manhattan
Também conhecida como distância de "quarteirão", a distância de Manhattan mede a soma total das diferenças absolutas ao longo de cada dimensão. Imagine que você está caminhando pelas ruas de uma cidade em forma de grade; a distância que você percorreria quarteirão por quarteirão é a distância de Manhattan. Esse método é particularmente útil em ambientes que imitam uma grade, como a navegação pelas ruas da cidade ou em alguns tipos de jogos. Também é útil quando você está lidando com dados de dimensões muito altas, em que a distância euclidiana pode se tornar menos confiável. Para saber mais, confira nosso tutorial sobre a distância de Manhattan.
Distância do cosseno
A distância cosseno analisa o ângulo entre dois pontos ou vetores. Em vez de se concentrar no comprimento da linha entre elas, ele considera como elas estão orientadas em relação umas às outras. Isso o torna especialmente útil em campos como análise de texto ou sistemas de recomendação, em que a direção dos dados (como contagem de palavras em artigos ou preferências do usuário) é mais importante do que a magnitude (quanto). Para obter um entendimento mais profundo, consulte nosso artigo sobre distância cosseno.
Distância de Chebyshev
A distância de Chebyshev é outra forma de medir a distância, concentrando-se na maior diferença ao longo de qualquer dimensão. É como jogar xadrez: o rei se move para a casa mais distante no menor número de movimentos, independentemente de ser horizontal, vertical ou diagonal. Essa métrica é particularmente útil em cenários em que você precisa considerar apenas a mais significativa das várias diferenças. Para saber mais, leia nosso tutorial sobre a distância de Chebyshev.
Limitações da distância euclidiana
Embora a distância euclidiana seja amplamente usada devido à sua natureza intuitiva e ao cálculo simples, ela tem algumas limitações notáveis. Entender isso pode ajudar você a escolher a medida de distância correta ou a ajustar os dados para atenuar esses problemas.
Sensibilidade da escala
A distância euclidiana pode ser afetada de forma desproporcional pela escala dos recursos. Por exemplo, em um conjunto de dados que contém renda e idade, a renda normalmente abrange uma faixa muito maior (talvez milhares ou dezenas de milhares) em comparação com a idade (geralmente até cerca de 100). Essa disparidade pode fazer com que a renda sobrecarregue o cálculo da distância, distorcendo os resultados em relação à sua escala.
Mitigação: A normalização ou padronização dos dados pode ajudar a equilibrar as escalas de diferentes recursos, garantindo que nenhum recurso único influencie indevidamente o cálculo da distância.
Maldição da dimensionalidade
A maldição da dimensionalidade refere-se a vários fenômenos que surgem à medida que o número de dimensões em um conjunto de dados aumenta. Uma delas é que o conceito de "proximidade" ou "distância" se torna menos significativo - as distâncias tendem a convergir, dificultando a distinção entre pontos próximos e distantes de forma eficaz.
Mitigação: Técnicas como a análise de componentes principais(PCA) ou a incorporação de vizinhos estocásticos distribuídos em t(t-SNE) reduzem a dimensionalidade dos dados. Esses métodos ajudam a destilar os recursos essenciais com a maior variação, o que pode ajudar a simplificar os dados.
Sensibilidade a exceções
Os cálculos de distância euclidiana também podem ser muito influenciados por outliers. Em espaços altamente dimensionais, um único outlier pode alterar drasticamente as distâncias, fazendo com que alguns pontos de dados pareçam muito mais semelhantes ou diferentes do que realmente são.
De fato, a sensibilidade da regressão linear aos outliers está relacionada ao conceito de distância euclidiana. Isso ocorre porque, na regressão linear, o modelo minimiza a soma dos resíduos ao quadrado, que são as diferenças entre os valores observados e previstos. Ao fazer isso, você mede essencialmente a distância euclidiana entre os pontos de dados observados e a linha de regressão. Os outliers podem afetar essa distância de forma desproporcional porque o quadrado de desvios maiores aumenta mais rapidamente do que os menores.
Mitigação: O uso de métricas mais robustas que sejam menos sensíveis a discrepâncias pode ajudar, como a distância de Manhattan para determinados tipos de dados. Além disso, o pré-processamento de dados para identificar e tratar os outliers, seja ajustando-os ou removendo-os, pode evitar que eles distorçam os cálculos de distância.
Abordagem alternativa: Outra estratégia é considerar a distância euclidiana ponderada. Essa variação da distância euclidiana atribui pesos diferentes a dimensões ou recursos diferentes, possivelmente reduzindo o peso daqueles que são propensos a discrepâncias ou ruídos.
Conclusão
Como já exploramos, a distância euclidiana é uma métrica fundamental em muitos campos analíticos e tecnológicos, fornecendo uma maneira direta de medir a distância em linha reta entre pontos. Compreender e utilizar a distância euclidiana pode aumentar a precisão e a eficácia de muitos aplicativos, desde algoritmos de aprendizado de máquina até análises espaciais.
Incentivo você a experimentar a distância euclidiana em seus projetos e a explorar outras oportunidades de aprendizado por meio de cursos como Designing Machine Learning Workflows in Python e Anomaly Detection in Python Course.
Torne-se um cientista de ML
Como um profissional experiente em ciência de dados, machine learning e IA generativa, Vinod se dedica a compartilhar conhecimento e capacitar aspirantes a cientistas de dados para que tenham sucesso nesse campo dinâmico.
Perguntas frequentes sobre a distância euclidiana
Por que a distância euclidiana é importante no aprendizado de máquina?
A distância euclidiana ajuda em vários algoritmos de aprendizado de máquina ao quantificar a semelhança ou a diferença entre os pontos de dados, o que é importante para tarefas como classificação, agrupamento e detecção de anomalias.
A distância euclidiana é sempre a melhor opção para medir distâncias na ciência de dados?
Nem sempre. A melhor métrica de distância depende do tipo de dados e do problema específico. Por exemplo, a distância de Manhattan pode ser mais apropriada para dados de alta dimensão ou situações em que o movimento em forma de grade é mais representativo.
Como a distância euclidiana lida com coordenadas negativas?
A distância euclidiana mede a diferença absoluta entre as coordenadas correspondentes, tratando todas as coordenadas da mesma forma, sejam elas positivas ou negativas.
A distância euclidiana pode ser usada com dados categóricos?
Não, a distância euclidiana geralmente requer entrada numérica para calcular as distâncias. Métodos alternativos, como a distância de Hamming ou outras medidas de similaridade personalizadas, são usados para dados categóricos.
Como a escolha da distância euclidiana afeta o desempenho de algoritmos de agrupamento como o k-means?
O uso da distância euclidiana em algoritmos de agrupamento, como o K-means, influencia diretamente o modo como os agrupamentos são formados, pois determina as propriedades geométricas desses agrupamentos. A distância euclidiana tende a formar clusters esféricos, em que a média serve como centro do cluster. Isso pode afetar o desempenho do clustering, especialmente quando os clusters naturais nos dados não são esféricos.


