Vorwärtspropagierung in neuronalen Netzen: Ein vollständiger Leitfaden

Neuronale Netze haben die künstliche Intelligenz revolutioniert und ermöglichen alles von der Bilderkennung bis zur Verarbeitung natürlicher Sprache. Das Herzstück dieser leistungsstarken Modelle ist ein grundlegender Prozess, die sogenannte Vorwärtsausbreitung. Dieser Leitfaden erforscht dieses Kernkonzept und führt dich von den Grundprinzipien bis zur praktischen Umsetzung. 

Wenn du nach einer praktischen Anleitung für viele der hier behandelten Konzepte suchst, solltest du dir unseren Deep Learning in Python Lernpfad.

Was ist Forward Propagation?

Vorwärtspropagation ist der Prozess, bei dem ein neuronales Netz Eingabedaten in Vorhersagen oder Ausgaben umwandelt. Stell dir das als die "Denkphase" eines neuronalen Netzes vor - wenn ein Input (z. B. ein Bild oder ein Text) gezeigt wird, verarbeitet das Netz diese Informationen durch seine Schichten, um ein Ergebnis zu erzielen.

Technisch gesehen handelt es sich um eine sequentielle Berechnung, die Daten von der Eingabeschicht über die verborgenen Schichten bis zur Ausgabeschicht bewegt. Während dieser Reise werden die Daten durch gewichtete Verbindungen und Aktivierungsfunktionen umgewandelt, so dass das Netz komplexe Muster erfassen kann.

Warum es wichtig ist, die Ausbreitung zu verstehen

Das Verständnis der Vorwärtsausbreitung ist aus mehreren Gründen wichtig:

1. Grundlage für das Lernen: Du kannst nicht verstehen, wie neuronale Netze lernen, ohne zu wissen, wie sie Vorhersagen machen. Vorwärtspropagation ist die Voraussetzung für das Verständnis der Backpropagationden Algorithmus, der das Lernen ermöglicht.
2. Fehlersuche und Optimierung: Wenn neuronale Netze nicht gut funktionieren, hilft dir das Wissen, wie die Daten durch das Netz fließen, Probleme zu erkennen und zu beheben.
3. Modelldesign: Um eine effektive Architektur zu entwerfen, muss man verstehen, wie sich Informationen durch die verschiedenen Schichtenkonfigurationen verbreiten.
4. Effizienz des Einsatzes: Die Optimierung der Vorwärtsausbreitung ist wichtig für den Einsatz von Modellen in ressourcenbeschränkten Umgebungen.

Das erfährst du in diesem Leitfaden

Am Ende dieses umfassenden Leitfadens wirst du:

• die Mathematik hinter den Berechnungen neuronaler Netze zu verstehen
• In der Lage sein, Vorwärtspropagation von Grund auf mit NumPy zu implementieren
• Wissen, wie man moderne Frameworks wie TensorFlow und PyTorch für effiziente Vorwärtspropagierung nutzt
• Visualisiere, wie sich Informationen verändern, während sie sich durch ein Netzwerk bewegen
• Verbinde die Vorwärtsausbreitung mit dem breiteren Lernprozess in neuronalen Netzen
• Implementiere ein vollständiges Arbeitsbeispiel mit echten Daten

Voraussetzungen

Um diesen Leitfaden optimal nutzen zu können, solltest du Folgendes mitbringen

• Grundlegende Kenntnisse der Python-Programmierung
• Vertrautheit mit grundlegenden mathematischen Konzepten (Vektoren, Matrizen und Grundrechenarten)
• Einige Erfahrung mit Konzepten des maschinellen Lernens

Wenn du dein Fundament stärken willst, solltest du diese Ressourcen in Betracht ziehen:

• Einführung in Tiefe Neuronale Netze Kurs für die wichtigsten Konzepte.
• Einführung in Deep Learning in Python Kurs für eine interaktive Lernerfahrung.
• Aufbau eines einfachen neuronalen Netzes von Grund auf Tutorium für praktische Übungen.

Auch ohne umfangreiches Hintergrundwissen haben wir diesen Leitfaden so gestaltet, dass die Konzepte schrittweise aufgebaut werden, damit auch entschlossene Lernende Zugang zu neuronalen Netzen haben. Lass uns eintauchen!

Grundlagen der Vorwärtsausbreitung

Um die Vorwärtsausbreitung zu verstehen, müssen wir mit ihren grundlegenden Bausteinen beginnen. Beginnen wir mit der kleinsten Recheneinheit in neuronalen Netzen und arbeiten uns schrittweise zu komplexeren Strukturen vor.

Das einzelne Neuron: Wo alles beginnt

Die Reise des neuronalen Netzwerks beginnt mit einer faszinierenden Parallele zur Biologie. So wie das menschliche Gehirn aus Milliarden miteinander verbundener Neuronen besteht, werden künstliche neuronale Netze aus mathematischen Modellen aufgebaut, die von diesen biologischen Zellen inspiriert sind.

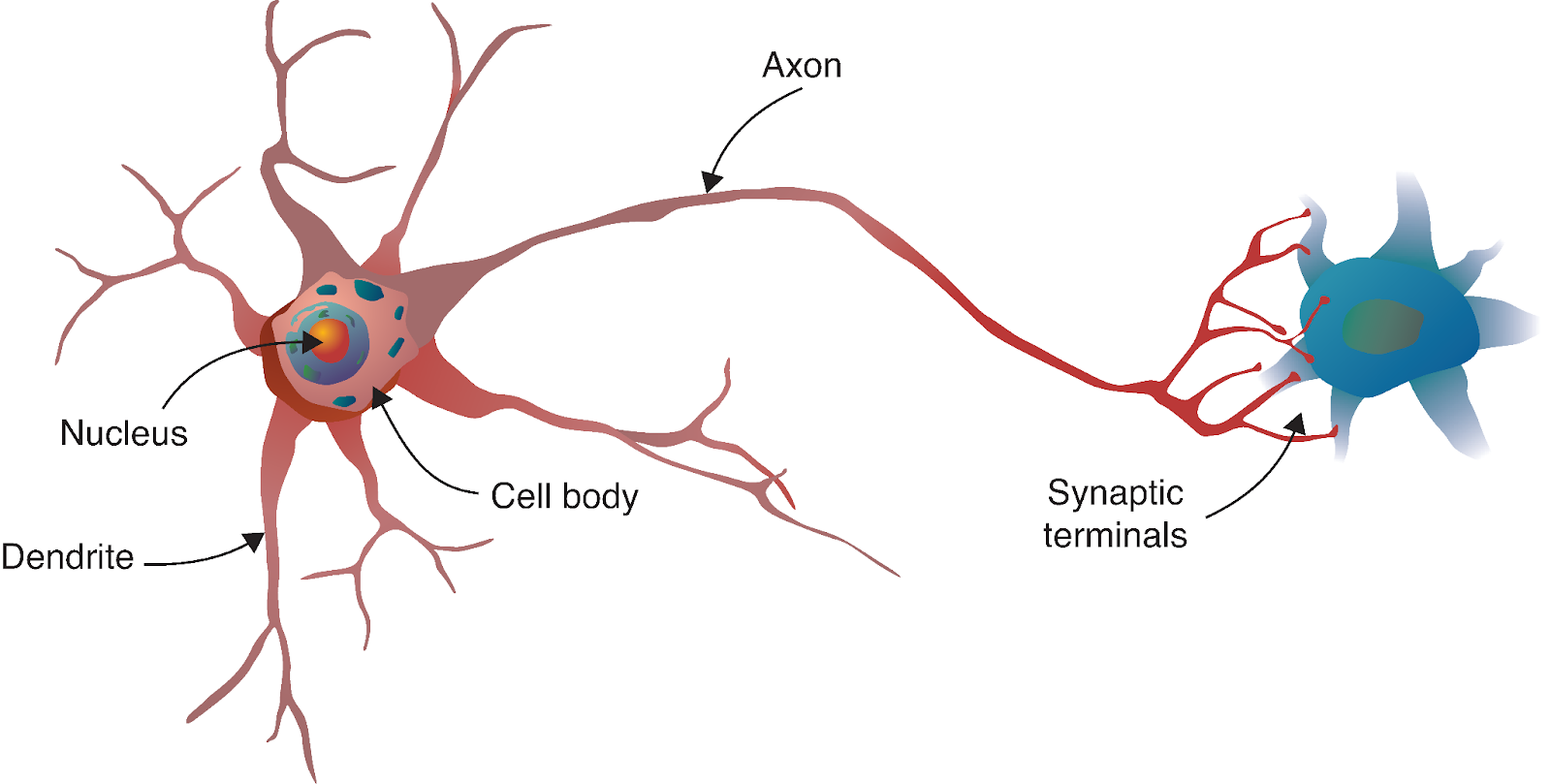
Quelle: Deep Learning - Visuelle Annäherung

Ein biologisches Neuron empfängt über Dendriten Signale von anderen Neuronen, verarbeitet diese Signale in seinem Zellkörper und leitet das Ergebnis dann über das Axon an andere Neuronen weiter. In unserem Berechnungsmodell spiegeln wir diesen Prozess mit:

• Eingänge: Die Signale, die in das Neuron gelangen (wie Dendriten, die Signale empfangen).
• Gewichte: Die Bedeutung, die jedem Input zugewiesen wird (analog zur Stärke der synaptischen Verbindungen).
• Bias: Ein zusätzlicher Parameter, der dazu beiträgt, dass das Neuron unabhängig von den Eingaben aktiviert wird oder inaktiv bleibt.
• Aktivierungsfunktion: Bestimmt, ob und wie stark das Neuron auf der Grundlage seiner Eingaben "feuert" (ähnlich wie der Zellkörper entscheidet, ob er ein Aktionspotenzial erzeugt).
• Ausgabe: Das Signal, das an die nächste Schicht gesendet wird (wie das Axon, das an andere Neuronen weiterleitet).

Um dies zu verdeutlichen, stellen wir uns ein einzelnes Neuron vor:

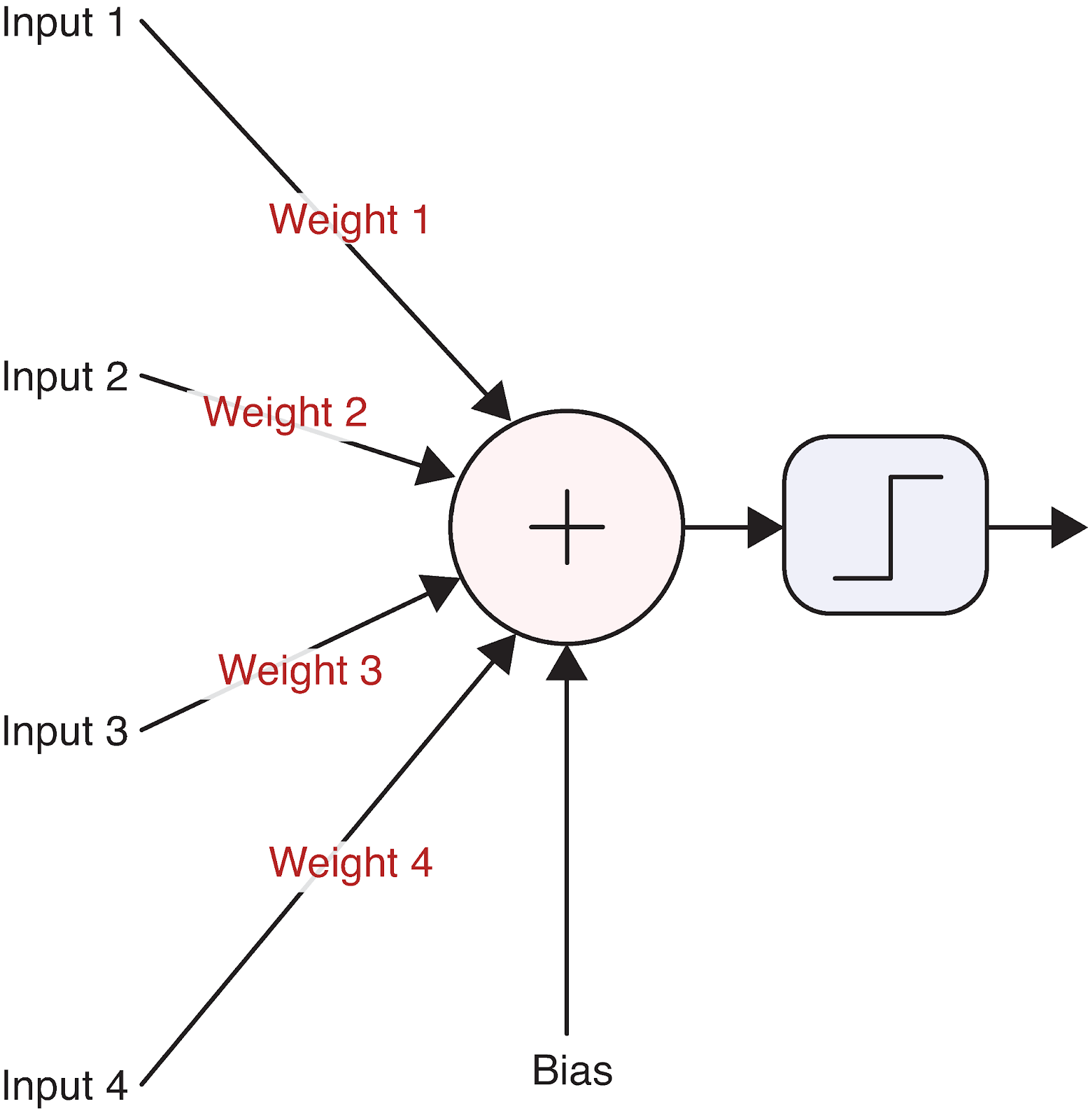
Quelle: Deep Learning - Visuelle Annäherung

Diese einfache Recheneinheit bildet die Grundlage selbst für die komplexesten neuronalen Netze. Aber wie genau wandelt ein Neuron seine Eingaben in eine Ausgabe um? An dieser Stelle kommt die Mathematik ins Spiel.

Mathematische Grundlage eines einzelnen Neurons

Die Funktionsweise eines Neurons kann mit einer einfachen Gleichung beschrieben werden:

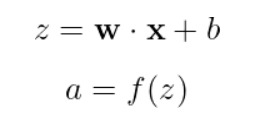
Aufgeschlüsselt:

• x ist unser Eingangsvektor [x_1, x_2, x_3, ...]
• w ist unser Gewichtsvektor [w_1, w_2, ..., w_n]
• b ist der Bias (ein einzelner skalarer Wert)
• z ist die gewichtete Summe plus Verzerrung (oft als "Voraktivierung" oder "Logit" bezeichnet)
• f ist die Aktivierungsfunktion
• a ist die endgültige Ausgabe des Neurons

Lass uns ein konkretes Beispiel mit reellen Zahlen durcharbeiten. Nehmen wir an, wir haben ein Neuron mit drei Eingängen:

Inputs: x = [2, 5, -1]
Weights: w = [0.5, -1, 2]
Bias: b = 0.5

Zuerst berechnen wir die gewichtete Summe plus Verzerrung:

Als nächstes wenden wir eine Aktivierungsfunktion an. Wir verwenden die beliebte ReLU-Funktion (Rectified Linear Unit), die wie folgt definiert ist:

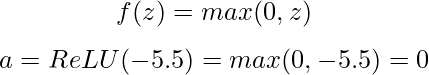
Bei einem negativen Voraktivierungswert gibt unser ReLU-Neuron 0 aus, d.h. es "feuert" nicht für diese bestimmte Eingabe.

Die Aktivierungsfunktion ist entscheidend, weil sie Nichtlinearität in das Netz einführt. Ohne sie wären neuronale Netze darauf beschränkt, nur lineare Beziehungen zu lernen, egal wie viele Schichten sie haben. Zu den gängigen Aktivierungsfunktionen gehören:

• Sigmoid: 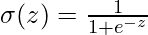gibt zwischen 0 und 1 aus, nützlich für die binäre Klassifizierung
• ReLU: 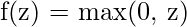einfach, effizient und hilft bei dem Problem des verschwindenden Gradienten
• Tanh: 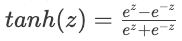- Gibt zwischen -1 und 1 aus, wird oft in versteckten Schichten verwendet

Jede Aktivierungsfunktion hat ihre Stärken und Anwendungsfälle, die wir bei der Implementierung unseres neuronalen Netzes genauer untersuchen werden.

Von Neuronen zu Schichten

Einzelne Neuronen sind leistungsstark, aber die wahre Stärke neuronaler Netze zeigt sich, wenn Neuronen in Schichten organisiert sind. Eine Schicht ist einfach eine Sammlung von Neuronen, die Eingaben parallel verarbeiten. In einem neuronalen Netz gibt es normalerweise drei Arten von Schichten:

1. Eingabeschicht: Empfängt die Rohdaten und gibt sie an die nächste Schicht weiter
2. Verborgene Schichten: Informationen aus den vorherigen Schichten verarbeiten
3. Ausgangsschicht: Erzeugt die endgültige Vorhersage oder Klassifizierung

Wenn wir mehrere Neuronen in einer Schicht haben, die alle dieselben Eingaben erhalten, aber unterschiedliche Gewichte und Vorspannungen haben, können wir dies effizient mit Matrixoperationen darstellen. Schauen wir mal, wie das funktioniert.

Stell dir vor, wir haben eine Schicht mit 3 Eingangswerten und 4 Neuronen. Jedes Neuron hat seinen eigenen Satz von Gewichten und Vorspannungen:

Inputs: x = [x₁, x₂, x₃]
Weights for neuron 1: w₁ = [w₁₁, w₁₂, w₁₃]
Weights for neuron 2: w₂ = [w₂₁, w₂₂, w₂₃]
Weights for neuron 3: w₃ = [w₃₁, w₃₂, w₃₃]
Weights for neuron 4: w₄ = [w₄₁, w₄₂, w₄₃]
Biases: b = [b₁, b₂, b₃, b₄]

Wir können diese Gewichte in einer Matrix W organisieren:

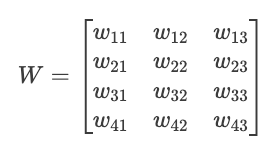
Jetzt können wir mit einer einzigen Matrixmultiplikation alle Voraktivierungen der Neuronen auf einmal berechnen:

Wo:

• X ist unser Eingangsvektor [x₁, x₂, x₃]
• W^T ist die Transponierung unserer Gewichtsmatrix
• B ist unser Bias-Vektor [b₁, b₂, b₃, b₄]
• Z ist der resultierende Vektor der Voraktivierungen [z₁, z₂, z₃, z₄]

Dann wenden wir die Aktivierungsfunktion elementweise an, um unsere endgültigen Ausgaben zu erhalten:

Diese Matrixdarstellung ist nicht nur mathematisch elegant, sondern auch rechnerisch effizient. Moderne Hardware (vor allem GPUs) ist für Matrixoperationen optimiert, so dass dieser Ansatz viel schneller ist als die Berechnung des Outputs jedes Neurons einzeln.

Die Fähigkeit, diese Schichten zu stapeln - wobei die Ausgabe einer Schicht zur Eingabe der nächsten wird - verleiht neuronalen Netzen ihre bemerkenswerte Fähigkeit, komplexe Muster zu lernen. Wenn wir diese Bausteine miteinander verbinden, können wir erforschen, wie die Vorwärtsausbreitung in einem ganzen neuronalen Netz funktioniert.

Vorwärtsausbreitung durch ein komplettes Netzwerk

Nachdem wir nun die einzelnen Neuronen und Schichten verstanden haben, wollen wir einen Schritt zurückgehen und sehen, wie die Vorwärtsausbreitung in einem ganzen neuronalen Netzwerk funktioniert. Hier zeigt sich die wahre Stärke von Deep Learning.

Mehrschichtige Netzwerke: das vollständige Bild

Ein vollständiges neuronales Netz besteht aus einer Eingabeschicht, einer oder mehreren verborgenen Schichten und einer Ausgabeschicht. Der Begriff "deep" in deep learning bezieht sich auf Netzwerke mit mehreren versteckten Schichten. Jede Schicht wandelt die Daten auf immer abstraktere Weise um, so dass das Netz komplexe Darstellungen lernen kann.

Betrachten wir ein einfaches neuronales Netz mit:

• Eine Eingabeschicht mit 4 Merkmalen
• Zwei versteckte Schichten mit 3 bzw. 2 Neuronen
• Eine Ausgabeschicht mit 3 Neuronen (vielleicht für die Klassifizierung mehrerer Klassen)

Optisch sieht dieses Netzwerk wie folgt aus:

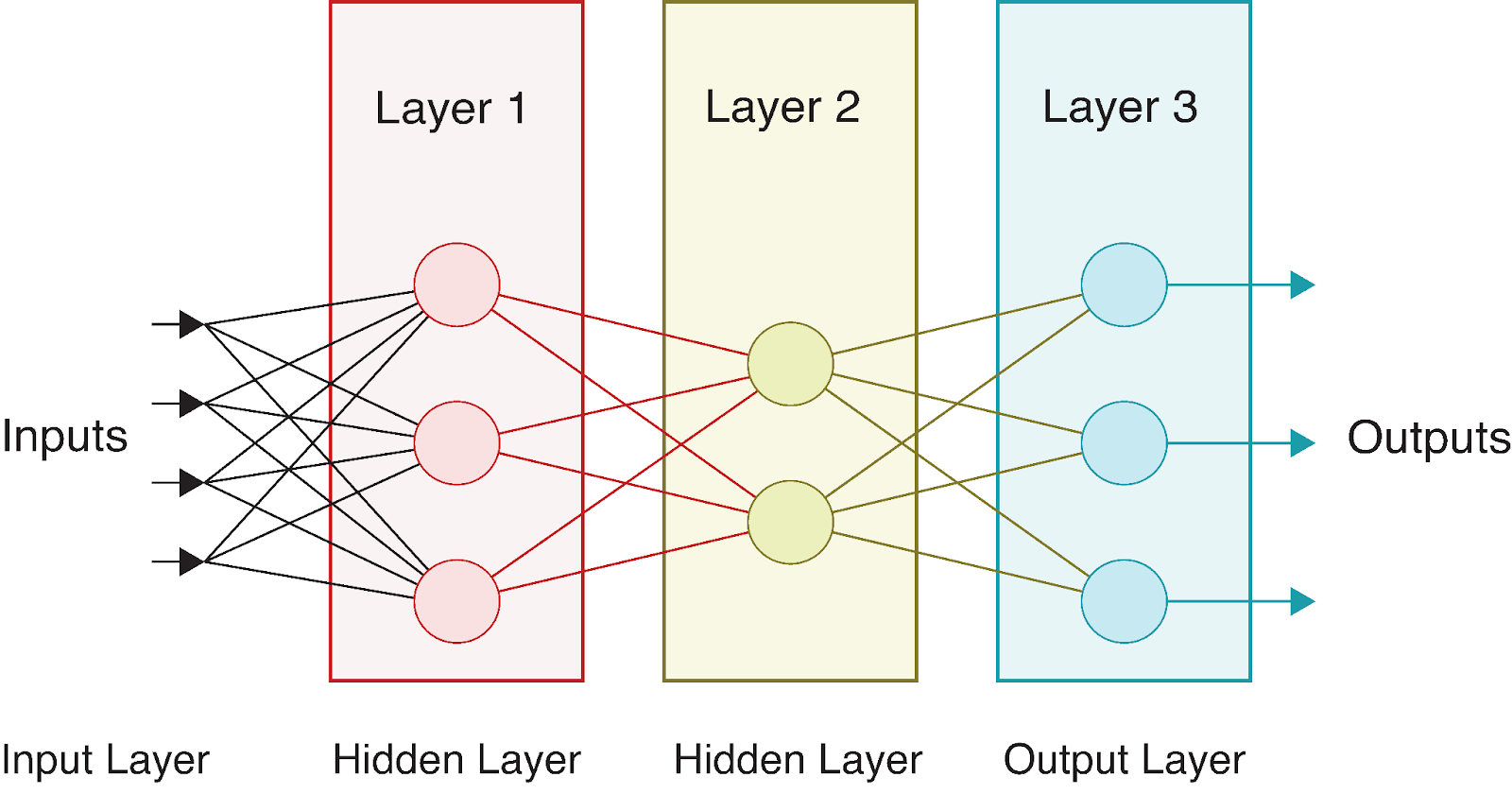
Während die Daten durch dieses Netzwerk fließen, führen wir auf jeder Ebene eine Reihe von Berechnungen durch. Wenn wir bezeichnen:

• Eingangsvektor als X = [x_1, x_2, x_3, x_4]
• Gewichtsmatrizen als 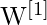(für die versteckte Schicht) und 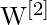(für die Ausgabeschicht)
• Bias-Vektoren als 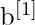und
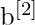
• Aktivierungsfunktionen als f1 (für die versteckte Schicht) und f2 (für die Ausgabeschicht)

Wir können die Vorwärtsausbreitung durch dieses gesamte Netzwerk wie folgt ausdrücken:

1. Berechne die Voraktivierungen der versteckten Schicht: 

2. Wende die Aktivierungsfunktion an, um die Ausgaben der versteckten Schicht zu erhalten: 

3. Berechne die Voraktivierungen der Ausgabeschicht: 

4. Wende die Aktivierungsfunktion an, um die endgültigen Ausgaben zu erhalten:

Die endgültige Ausgabe A^[2] stellt die Vorhersage des Netzwerks dar. Bei Klassifizierungsproblemen können dies Wahrscheinlichkeiten für jede Klasse sein, bei Regressionen die vorhergesagten Werte.

Verschiedene Schichten verwenden oft unterschiedliche Aktivierungsfunktionen. Versteckte Schichten verwenden z.B. üblicherweise ReLU, während die Ausgabeschichten ReLU verwenden können:

• Sigmoid für binäre Klassifizierung
• Softmax für Mehrklassen-Klassifizierung
• Linear (keine Aktivierung) für Regression

Das Schöne an dieser mehrschichtigen Struktur ist, dass jede Schicht lernen kann, verschiedene Aspekte der Daten darzustellen. Frühe Schichten erkennen in der Regel einfache Merkmale, während tiefere Schichten diese zu komplexeren Mustern kombinieren. Dieses hierarchische Lernen macht neuronale Netze so leistungsfähig für komplexe Aufgaben wie Bild- und Spracherkennung.

Algorithmus zur Vorwärtsausbreitung

Lass uns den Prozess der Vorwärtsausbreitung in einen Algorithmus umwandeln. Bei einem neuronalen Netz mit L Schichten erfolgt die Vorwärtspropagation in folgenden Schritten:

# Pseudocode for forward propagation
def forward_propagation(X, parameters):
   """
   X: Input data (batch_size, n_features)
   parameters: Dictionary containing weights and biases for each layer
   Returns: The final output and all intermediate activations
   """
   # Store all activations for later use (e.g., in backpropagation)
   activations = {'A0': X}  # A0 is the input
  
   # Loop through L-1 layers (excluding the output layer)
   for l in range(1, L):
       # Get previous activation
       A_prev = activations[f'A{l-1}']
      
       # Get weights and biases for current layer
       W = parameters[f'W{l}']
       b = parameters[f'b{l}']
      
       # Compute pre-activation
       Z = np.dot(A_prev, W.T) + b
      
       # Apply activation function (e.g., ReLU for hidden layers)
       A = relu(Z)
      
       # Store values for later use
       activations[f'Z{l}'] = Z
       activations[f'A{l}'] = A
  
   # Compute output layer (layer L)
   A_prev = activations[f'A{L-1}']
   W = parameters[f'W{L}']
   b = parameters[f'b{L}']
  
   # Compute pre-activation for output layer
   Z = np.dot(A_prev, W.T) + b
  
   # Apply output activation function (depends on the task)
   if task == 'binary_classification':
       A = sigmoid(Z)
   elif task == 'multiclass_classification':
       A = softmax(Z)
   elif task == 'regression':
       A = Z  # Linear activation
  
   # Store output layer values
   activations[f'Z{L}'] = Z
   activations[f'A{L}'] = A
  
   return A, activations

Dieser Algorithmus hebt mehrere wichtige Aspekte der Vorwärtsausbreitung hervor:

1. Sequentielle Verarbeitung: Informationen fließen strikt vorwärts, Schicht für Schicht.
2. Aktivierungsspeicher: Wir speichern nicht nur die endgültige Ausgabe, sondern auch alle Zwischenaktivierungen, die für das Training des Netzes mit Backpropagation wichtig sind.
3. Aufgabenspezifische Ausgabe: Die Aktivierungsfunktion für die Ausgabeschicht wird je nach Problemstellung (Klassifizierung oder Regression) ausgewählt.

Der Algorithmus der Vorwärtspropagation ist bemerkenswert einfach und ermöglicht es neuronalen Netzen dennoch, unglaublich komplexe Funktionen zu approximieren. In Kombination mit dem richtigen Training durch Backpropagation ermöglicht dieser einfache Prozess dem Netzwerk, aus Daten zu lernen und immer genauere Vorhersagen zu treffen.

Lass uns ein konkretes Beispiel durchgehen, um unser Verständnis zu vertiefen. Nehmen wir an, der Input X = [0,5, -0,2, 0,1] durchläuft unser Beispielnetz mit:

• Gewichte der versteckten Schicht W^[1] (4×3-Matrix) und Verzerrungen b^[1] (Vektor aus 4 Werten)
• Gewichte der Ausgangsschicht W^[2] (2×4-Matrix) und Verzerrungen b^[2] (Vektor aus 2 Werten)

Der Einfachheit halber nehmen wir an, dass alle Gewichte 0,1 und alle Verzerrungen 0 sind:

X = [0.5, -0.2, 0.1]
W[1] = [[0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1]]
b[1] = [0, 0, 0, 0]
W[2] = [[0.1, 0.1, 0.1, 0.1], [0.1, 0.1, 0.1, 0.1]]
b[2] = [0, 0]

Folge unserem Algorithmus:

• Erster Schritt:

• Zweiter Schritt mit ReLU: 

• Dritter Schritt:

• Vierter Schritt mit der Verwendung von Sigmoid: 

Damit haben wir unsere endgültige Vorhersage. In einem binären Klassifizierungskontext würden diese Werte nahe 0,5 die Unsicherheit zwischen den beiden Klassen anzeigen.

Im nächsten Abschnitt werden wir die Vorwärtsausbreitung in Python implementieren, um diese Berechnungen in Aktion zu sehen.

Implementierung von Forward Propagation in Python

Nachdem wir nun die Theorie der Vorwärtsausbreitung verstanden haben, wollen wir sie in die Praxis umsetzen, indem wir sie in Python implementieren. Wir beginnen mit einer Implementierung "von Grund auf" nur mit NumPy und sehen dann, wie moderne Deep Learning Frameworks diesen Prozess vereinfachen.

Von Grund auf mit NumPy bauen

NumPy bietet effiziente Array-Operationen, mit denen wir die besprochenen Matrixberechnungen durchführen können. Lass uns eine einfache neuronale Netzwerkklasse bauen, die eine Vorwärtspropagation durch mehrere Schichten durchführt.

Zuerst müssen wir die notwendigen Bibliotheken importieren:

import numpy as np
import matplotlib.pyplot as plt

# For reproducibility
np.random.seed(42)

Definieren wir nun die Aktivierungsfunktionen, die wir in unserem Netz verwenden werden:

def relu(Z):
   """ReLU activation function: max(0, Z)"""
   return np.maximum(0, Z)

def sigmoid(Z):
   """Sigmoid activation function: 1/(1 + e^(-Z))"""
   return 1 / (1 + np.exp(-Z))

def softmax(Z):
   """Softmax activation function for multi-class classification"""
   # Subtract max for numerical stability (prevents overflow)
   exp_Z = np.exp(Z - np.max(Z, axis=1, keepdims=True))
   return exp_Z / np.sum(exp_Z, axis=1, keepdims=True)

Als Nächstes wollen wir eine Klasse für unser neuronales Netz erstellen:

class NeuralNetwork:
   def __init__(self, layer_dims, activations):
       """
       Initialize a neural network with specified layer dimensions and activations
      
       Parameters:
       - layer_dims: List of integers representing the number of neurons in each layer
                    (including input and output layers)
       - activations: List of activation functions for each layer (excluding input layer)
       """
       self.L = len(layer_dims) - 1  # Number of layers (excluding input layer)
       self.layer_dims = layer_dims
       self.activations = activations
       self.parameters = {}
      
       # Initialize parameters (weights and biases)
       self.initialize_parameters()
  
   def initialize_parameters(self):
       """Initialize weights and biases with small random values"""
       for l in range(1, self.L + 1):
           # He initialization for weights - helps with training deep networks
           self.parameters[f'W{l}'] = np.random.randn(self.layer_dims[l], self.layer_dims[l-1]) * np.sqrt(2 / self.layer_dims[l-1])
           self.parameters[f'b{l}'] = np.zeros((self.layer_dims[l], 1))
  
   def forward_propagation(self, X):
       """
       Perform forward propagation through the network
      
       Parameters:
       - X: Input data (n_features, batch_size)
      
       Returns:
       - AL: Output of the network
       - caches: Dictionary containing all activations and pre-activations
       """
       caches = {}
       A = X  # Input layer activation
       caches['A0'] = X
      
       # Process through L-1 layers (excluding output layer)
       for l in range(1, self.L):
           A_prev = A
          
           # Get weights and biases for current layer
           W = self.parameters[f'W{l}']
           b = self.parameters[f'b{l}']
          
           # Forward propagation for current layer
           Z = np.dot(W, A_prev) + b
          
           # Apply activation function
           activation_function = self.activations[l-1]
           if activation_function == "relu":
               A = relu(Z)
           elif activation_function == "sigmoid":
               A = sigmoid(Z)
          
           # Store values for backpropagation
           caches[f'Z{l}'] = Z
           caches[f'A{l}'] = A
      
       # Output layer
       W = self.parameters[f'W{self.L}']
       b = self.parameters[f'b{self.L}']
       Z = np.dot(W, A) + b
      
       # Apply output activation function
       activation_function = self.activations[self.L-1]
       if activation_function == "sigmoid":
           AL = sigmoid(Z)
       elif activation_function == "softmax":
           AL = softmax(Z)
       elif activation_function == "linear":
           AL = Z  # No activation for regression
      
       # Store output layer values
       caches[f'Z{self.L}'] = Z
       caches[f'A{self.L}'] = AL
      
       return AL, caches

Die Klasse NeuralNetwork, die wir oben implementiert haben, bietet ein komplettes Framework für die Erstellung und Verwendung eines neuronalen Netzwerks mit anpassbarer Architektur. Schauen wir uns seine wichtigsten Bestandteile an:

1. Initialisierung: Das Netz wird mit bestimmten Schichtdimensionen und Aktivierungsfunktionen konfiguriert. Es initialisiert automatisch die Gewichte und Verzerrungen mit der He-Initialisierungsmethode, um die Trainingsleistung zu verbessern.
2. Vorwärtsausbreitung: Die forward_propagation Methode, die wir gerade implementiert haben, ist das Herzstück der Vorhersagefähigkeit des neuronalen Netzes. Es:

• Nimmt Eingabedaten und leitet sie durch jede Schicht
• Wendet die entsprechende Aktivierungsfunktion in jeder Schicht an
• Speichert Zwischenwerte in Caches für die spätere Verwendung in der Backpropagation
• Gibt sowohl die endgültige Ausgabe als auch alle zwischengespeicherten Werte zurück

3. Aktivierungsfunktionen: Das Netzwerk unterstützt mehrere Aktivierungsfunktionen, darunter ReLU, Sigmoid und Softmax, sodass es verschiedene Arten von Problemen (Regression oder Klassifizierung) bearbeiten kann.

4. Flexible Architektur: Die Implementierung ermöglicht Netze beliebiger Tiefe und Breite und eignet sich damit für eine Vielzahl von maschinellen Lernaufgaben.

Diese Implementierung folgt dem Standardmuster für neuronale Netze, bei dem die Daten vorwärts durch das Netz fließen, wobei jede Schicht die Daten umwandelt, bevor sie sie an die nächste Schicht weitergibt.

Jetzt wollen wir unsere Implementierung mit einem kleinen Beispielnetzwerk testen:

# Create a sample network
# Input layer: 3 features
# Hidden layer 1: 4 neurons with ReLU activation
# Output layer: 2 neurons with sigmoid activation (binary classification)
layer_dims = [3, 4, 2]
activations = ["relu", "sigmoid"]
nn = NeuralNetwork(layer_dims, activations)

# Create sample input data - 3 features for 5 examples
X = np.random.randn(3, 5)

# Perform forward propagation
output, caches = nn.forward_propagation(X)

print(f"Input shape: {X.shape}")
print(f"Output shape: {output.shape}")
print(f"Output values:\n{output}")

Output:

Input shape: (3, 5)
Output shape: (2, 5)
Output values:
[[0.00386784 0.54343014 0.39661893 0.5        0.51056934]
[0.11877049 0.32541093 0.44840699 0.5        0.45586633]]

Lass uns auch visualisieren, wie sich die Daten verändern, während sie durch das Netzwerk fließen:

def visualize_activations(caches, example_idx=0):
   """Visualize the activations for a single example through the network"""
   plt.figure(figsize=(15, 6))
  
   # Plot input
   plt.subplot(1, 3, 1)
   plt.bar(range(caches['A0'].shape[0]), caches['A0'][:, example_idx])
   plt.title('Input Layer')
   plt.xlabel('Feature')
   plt.ylabel('Value')
  
   # Plot hidden layer activation
   plt.subplot(1, 3, 2)
   plt.bar(range(caches['A1'].shape[0]), caches['A1'][:, example_idx])
   plt.title('Hidden Layer (ReLU Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   # Plot output layer
   plt.subplot(1, 3, 3)
   plt.bar(range(caches['A2'].shape[0]), caches['A2'][:, example_idx])
   plt.title('Output Layer (Sigmoid Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   plt.tight_layout()
   plt.show()

# Visualize the first example
visualize_activations(caches)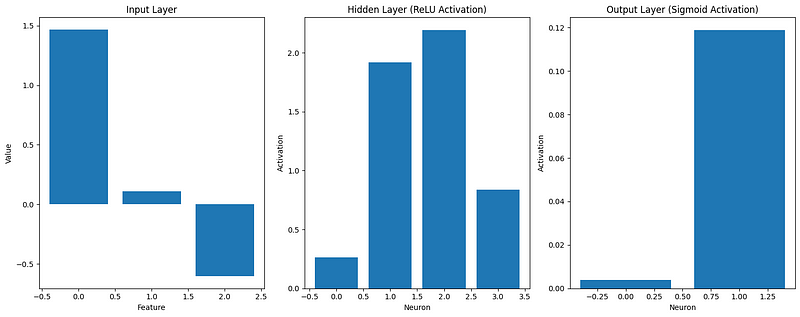

Diese Visualisierung hilft uns zu verstehen, wie die Eingabedaten umgewandelt werden, während sie sich durch das Netzwerk ausbreiten. Das können wir sehen:

1. Die Eingangsmerkmale können positive oder negative Werte haben
2. Nach der ReLU-Aktivierung in der versteckten Schicht sind alle Aktivierungen nicht-negativ
3. Die sigmoidale Aktivierung in der Ausgabeschicht beschränkt Werte zwischen 0 und 1

Unsere Implementierung "von Grund auf" demonstriert die Grundprinzipien der Vorwärtspropagation, aber moderne Deep-Learning-Frameworks bieten effizientere und flexiblere Werkzeuge für den Aufbau neuronaler Netze.

Einsatz von Deep Learning-Frameworks

Nun wollen wir dasselbe neuronale Netzwerk mit gängigen Deep-Learning-Frameworks implementieren: TensorFlow und PyTorch. Diese Frameworks optimieren die Leistung und bieten Abstraktionen auf höherer Ebene, was die Erstellung komplexer Modelle erleichtert.

Schauen wir uns zunächst die TensorFlow/Keras-Implementierung an:

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Input

# For reproducibility
tf.random.set_seed(42)

# Create the same network architecture
tf_model = Sequential([
   Input(shape=(3,)),  # Input layer with 3 features
   Dense(4, activation='relu'),  # Hidden layer with 4 neurons
   Dense(2, activation='sigmoid')  # Output layer with 2 neurons
])

tf_model.summary()

# Sample input data with the shape expected by Keras
X_tf = np.random.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in TensorFlow
tf_output = tf_model.predict(X_tf)

print(f"TensorFlow output shape: {tf_output.shape}")
print(f"TensorFlow output values:\n{tf_output}")

TensorFlow output shape: (5, 2)
TensorFlow output values:
[[0.6855308  0.7139542 ]
[0.4952355  0.5231934 ]
[0.50174904 0.5198488 ]
[0.44331825 0.6860926 ]
[0.6624589  0.5385444 ]]

Wir haben gerade unser neuronales Netzwerk mit TensorFlow/Keras implementiert und erfolgreich Vorwärtspropagation auf einigen Beispieldaten durchgeführt. Die Modellzusammenfassung zeigt unsere Architektur mit einer Eingabeschicht, die 3 Merkmale annimmt, einer versteckten Schicht mit 4 Neuronen, die eine ReLU-Aktivierung verwenden, und einer Ausgabeschicht mit 2 Neuronen, die eine Sigmoid-Aktivierung verwenden. Insgesamt hat das Modell 26 trainierbare Parameter.

Die Ergebnisse der Vorwärtspropagation zeigen die Ausgangsform (5, 2), die unseren 5 Eingangsbeispielen entspricht und jeweils 2 Ausgangswerte erzeugt. Diese Ausgänge sind aufgrund der sigmoidalen Aktivierungsfunktion in der Ausgabeschicht auf einen Wert zwischen 0 und 1 beschränkt.

Als Nächstes wollen wir sehen, wie wir dieselbe neuronale Netzwerkarchitektur mit PyTorch, einem anderen beliebten Deep-Learning-Framework, implementieren können, um die Ansätze zu vergleichen.

import torch
import torch.nn as nn

# For reproducibility
torch.manual_seed(42)

# Create a network in PyTorch
class PyTorchNN(nn.Module):
   def __init__(self):
       super(PyTorchNN, self).__init__()
       self.hidden = nn.Linear(3, 4)  # 3 inputs, 4 hidden neurons
       self.relu = nn.ReLU()
       self.output = nn.Linear(4, 2)  # 4 inputs from hidden, 2 outputs
       self.sigmoid = nn.Sigmoid()
  
   def forward(self, x):
       x = self.relu(self.hidden(x))
       x = self.sigmoid(self.output(x))
       return x

# Instantiate the model
torch_model = PyTorchNN()

# Print model structure
print(torch_model)

Output:

PyTorchNN(
 (hidden): Linear(in_features=3, out_features=4, bias=True)
 (relu): ReLU()
 (output): Linear(in_features=4, out_features=2, bias=True)
 (sigmoid): Sigmoid()
)

```python
# Sample input data
X_torch = torch.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in PyTorch
torch_output = torch_model(X_torch)

print(f"PyTorch output shape: {torch_output.shape}")
print(f"PyTorch output values:\n{torch_output}")

Output:

PyTorch output shape: torch.Size([5, 2])
PyTorch output values:
tensor([[0.4516, 0.4116],
       [0.4289, 0.4267],
       [0.4278, 0.4172],
       [0.3771, 0.4321],
       [0.5769, 0.3328]], grad_fn=<SigmoidBackward0>)

Lass uns unsere Implementierungen vergleichen:

# Compare dimensions and structure of outputs
print("\nComparison of implementations:")
print(f"NumPy output shape: {output.shape}")
print(f"TensorFlow output shape: {tf_output.shape}")
print(f"PyTorch output shape: {torch_output.shape}")

Output:

Comparison of implementations:
NumPy output shape: (2, 5)
TensorFlow output shape: (5, 2)
PyTorch output shape: torch.Size([5, 2])

Die wichtigsten Unterschiede zwischen unseren Umsetzungen:

1. Struktur und Lesbarkeit:

• NumPy: Explizite Implementierung jedes Schritts bietet vollständige Kontrolle und Transparenz
• TensorFlow/Keras: Abstraktionen auf hoher Ebene verbergen Implementierungsdetails, machen den Code aber einfacher
• PyTorch: Objektorientierter Ansatz mit expliziter Vorwärtsmethode

2. Leistung:

• TensorFlow und PyTorch optimieren Operationen für GPU-Beschleunigung
• Beide Frameworks implementieren effiziente Gradientenberechnungen für das Training
• Frameworks optimieren die Speichernutzung für große Netzwerke

3. Erweiterbarkeit:

• Frameworks bieten vorgefertigte Komponenten (Schichten, Optimierer usw.)
• Eingebaute Tools zum Speichern/Laden von Modellen, zur Visualisierung und zum Einsatz
• Umfangreiche Community-Unterstützung und Dokumentation

Für einfache Netzwerke funktioniert unsere NumPy-Implementierung gut, aber wenn die Komplexität zunimmt, werden Deep-Learning-Frameworks unerlässlich. Sie kümmern sich um Low-Level-Optimierungen und bieten Werkzeuge für den gesamten Workflow des maschinellen Lernens, von der Entwicklung bis zum Einsatz. Wenn du mehr über diese Frameworks erfahren möchtest, schau dir unsere separaten Leitfäden an:

• PyTorch Tutorial: Ein einfaches neuronales Netz von Grund auf aufbauen
• TensorFlow Tutorial für Einsteiger 

Im nächsten Abschnitt werden wir ein vollständiges Arbeitsbeispiel erstellen, das die Vorwärtspropagation auf ein reales Problem anwendet.

Beispiel für Vorwärtspropagation

Nachdem wir nun die Vorwärtspropagation sowohl von Grund auf als auch mit Hilfe gängiger Frameworks implementiert haben, wollen wir sie bei einem realen Problem in Aktion sehen. Wir werden ein komplettes Beispiel erstellen und untersuchen, wie man den Prozess für eine bessere Leistung optimieren kann.

Vollständiges Arbeitsbeispiel

Wenden wir unser Verständnis auf ein klassisches Problem des maschinellen Lernens an: die Erkennung handgeschriebener Ziffern anhand des MNIST-Datensatzes. Dieser Datensatz enthält 70.000 Bilder von handgeschriebenen Ziffern (0-9), die jeweils 28x28 Pixel groß sind.

Zuerst müssen wir die Daten laden und vorbereiten:

from tensorflow.keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt

# Load MNIST dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# Normalize pixel values to range [0, 1]
X_train = X_train / 255.0
X_test = X_test / 255.0

# Reshape images to vectors (flatten 28x28 to 784)
X_train_flat = X_train.reshape(X_train.shape[0], -1).T  # Shape: (784, 60000)
X_test_flat = X_test.reshape(X_test.shape[0], -1).T     # Shape: (784, 10000)

# Convert labels to one-hot encoding
def one_hot_encode(y, num_classes=10):
   one_hot = np.zeros((num_classes, y.size))
   one_hot[y, np.arange(y.size)] = 1
   return one_hot

y_train_one_hot = one_hot_encode(y_train)  # Shape: (10, 60000)
y_test_one_hot = one_hot_encode(y_test)    # Shape: (10, 10000)

# Display sample images
plt.figure(figsize=(10, 5))
for i in range(5):
   plt.subplot(1, 5, i+1)
   plt.imshow(X_train[i], cmap='gray')
   plt.title(f"Label: {y_train[i]}")
   plt.axis('off')
plt.tight_layout()
plt.show()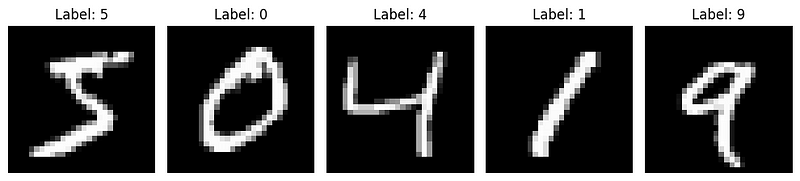

Jetzt wollen wir mit unserer NumPy-Implementierung ein neuronales Netzwerk für diese Aufgabe erstellen. Wir schaffen ein Netzwerk mit:

• Eingabeschicht: 784 Neuronen (28x28 Pixel)
• Verdeckte Schicht: 128 Neuronen mit ReLU-Aktivierung
• Ausgangsschicht: 10 Neuronen mit Softmax-Aktivierung (für 10 Ziffern)

# Define our network architecture
layer_dims = [784, 128, 10]
activations = ["relu", "softmax"]
nn = NeuralNetwork(layer_dims, activations)

# Take a small batch for demonstration
batch_size = 64
batch_indices = np.random.choice(X_train_flat.shape[1], batch_size, replace=False)
X_batch = X_train_flat[:, batch_indices]
y_batch = y_train_one_hot[:, batch_indices]

# Perform forward propagation
output, caches = nn.forward_propagation(X_batch)

# Compute accuracy
predictions = np.argmax(output, axis=0)
true_labels = np.argmax(y_batch, axis=0)
accuracy = np.mean(predictions == true_labels)

print(f"Batch accuracy: {accuracy:.4f}")

Out: Batch accuracy: 0.0781

Wir haben eine Genauigkeit von 7 %, was sogar schlechter ist als ein Modell, das zufällig rät. Das ist aber zu erwarten, da wir nur eine Vorwärtsausbreitung durchführen - es ist kein Lernen involviert.

Jetzt wollen wir uns ansehen, wie das Netzwerk ein einzelnes Bild durch die einzelnen Schichten verarbeitet:

def visualize_network_processing(nn, image, label, caches):
   """Visualize network processing for a single image"""
   plt.figure(figsize=(15, 10))
  
   # Plot original image
   plt.subplot(2, 3, 1)
   plt.imshow(image.reshape(28, 28), cmap='gray')
   plt.title(f"Input Image (Digit: {label})")
   plt.axis('off')
  
   # Plot flattened input (first 100 values)
   plt.subplot(2, 3, 2)
   plt.bar(range(100), image.flatten()[:100])
   plt.title("Input Layer (first 100 pixels)")
   plt.xlabel("Pixel Index")
   plt.ylabel("Pixel Value")
  
   # Plot hidden layer activations (first 50 neurons)
   plt.subplot(2, 3, 3)
   hidden_activations = caches['A1'][:50, 0]
   plt.bar(range(len(hidden_activations)), hidden_activations)
   plt.title("Hidden Layer Activations (first 50 neurons)")
   plt.xlabel("Neuron Index")
   plt.ylabel("Activation")
  
   # Plot output layer activations
   plt.subplot(2, 3, 4)
   output_activations = caches['A2'][:, 0]
   plt.bar(range(10), output_activations)
   plt.xticks(range(10))
   plt.title("Output Layer Activations (Softmax)")
   plt.xlabel("Digit Class")
   plt.ylabel("Probability")
  
   # Plot prediction vs actual
   plt.subplot(2, 3, 5)
   prediction = np.argmax(output_activations)
   plt.bar(['Actual', 'Predicted'], [label, prediction], color=['blue', 'orange'])
   plt.title(f"Prediction: {prediction}, Actual: {label}")
   plt.ylabel("Digit")
  
   plt.tight_layout()
   plt.show()

# Visualize forward propagation for the first image in our batch
image_idx = 0
image = X_batch[:, image_idx].reshape(784, 1)
label = true_labels[image_idx]

visualize_network_processing(nn, image, label, caches)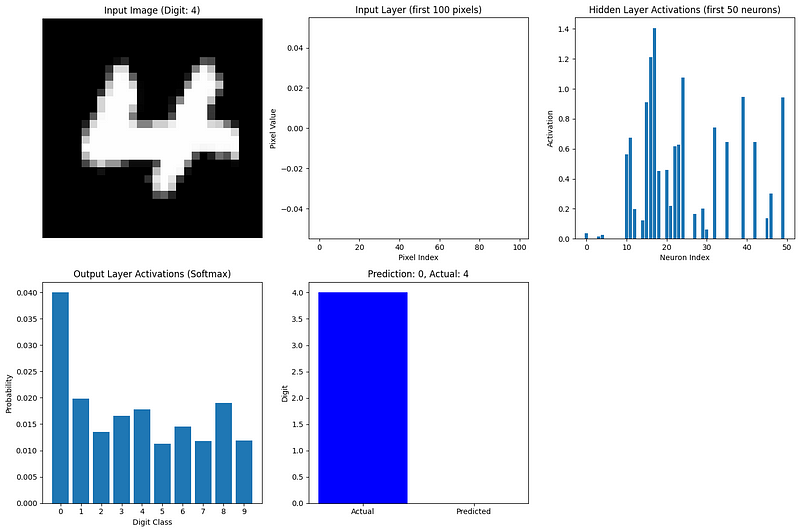

Diese Visualisierung zeigt, wie Informationen durch unser Netzwerk fließen:

1. Eingabeschicht: Die abgeflachten Bildpunkte (Werte zwischen 0 und 1)
2. Verdeckte Schicht: Die ReLU-aktivierten Neuronen erfassen verschiedene Merkmale der Ziffer
3. Ausgangsschicht: Die Softmax-Aktivierung ergibt eine Wahrscheinlichkeitsverteilung über die 10 möglichen Ziffern

Das aktivste Ausgangsneuron entspricht der Vorhersage des Netzes. Selbst mit zufälligen Gewichten (da wir das Netz noch nicht trainiert haben) können wir sehen, wie die Vorwärtspropagation die Eingabedaten in eine Vorhersage verwandelt.

Für ein umfassenderes Beispiel würden wir dieses Netzwerk mit Backpropagation trainieren, um die Gewichte und Verzerrungen anzupassen und die Vorhersagen mit der Zeit zu verbessern. Aber auch ohne Training demonstriert dieses Beispiel den Prozess der Vorwärtspropagation an realen Daten.

Optimierung der Vorwärtsausbreitung

Da neuronale Netze immer größer und die Datensätze immer umfangreicher werden, wird die Optimierung der Vorwärtspropagation immer wichtiger. Hier sind die wichtigsten Strategien, um die Vorwärtsausbreitung effizienter zu machen:

1. Stapelverarbeitung

Anstatt ein Beispiel nach dem anderen zu verarbeiten, berechnen wir die Vorwärtsausbreitung für eine Reihe von Beispielen gleichzeitig. Dadurch werden die parallelen Verarbeitungsmöglichkeiten moderner Hardware genutzt.

2. Vektorisierung

Die Verwendung von Matrixoperationen anstelle von Schleifen beschleunigt die Berechnungen dramatisch. Deshalb verwendet unsere Implementierung die Array-Operationen von NumPy.

3. Speicherverwaltung

Bei großen Netzwerken müssen wir auf die Speichernutzung achten. Zu den Techniken gehören:

• Wiederverwendung von Speicher für Zwischenaktivierungen.
• Berechne die Aktivierungen Schicht für Schicht, ohne alle Zwischenschritte zu speichern.
• Verwendung von Darstellungen mit geringerer Genauigkeit (z. B. 16-Bit-Gleitkommazahlen anstelle von 32-Bit).

4. GPU-Beschleunigung

Grafikprozessoren eignen sich besonders gut für Matrixoperationen. Moderne Frameworks können Berechnungen nahtlos auf GPUs verlagern und so die Geschwindigkeit deutlich erhöhen:

# TensorFlow example of GPU acceleration
import tensorflow as tf

# Check for available GPUs
print("GPUs Available:", tf.config.list_physical_devices('GPU'))

# TensorFlow automatically uses available GPUs
with tf.device('/GPU:0'):  # Explicitly specify GPU if multiple are available
   # Computation runs on GPU if available
   result = tf_model.predict(X_tf)

5. Spezialisierte Hardware

Neben den GPUs gibt es Hardware wie die Tensor Processing Units (TPUs) von Google, die speziell für neuronale Netzwerke entwickelt wurden.

6. Algorithmische Optimierungen

Bestimmte Aktivierungsfunktionen und Netzarchitekturen sind auf Recheneffizienz ausgelegt:

• ReLU ist schneller zu berechnen als Sigmoid oder tanh.
• Tiefenweise trennbare Faltungen reduzieren den Rechenaufwand im Vergleich zu Standardfaltungen.
• Durch das Pruning des Netzwerks werden überflüssige Verbindungen entfernt, was den Rechenaufwand reduziert.

7. Framework-Optimierungen

Deep Learning-Frameworks implementieren zahlreiche Low-Level-Optimierungen:

• Fused Operations kombinieren mehrere Schritte zu einem einzigen optimierten Kernel.
• Automatisch abgestimmte Algorithmen wählen die schnellste Implementierung für eine bestimmte Hardware.
• Die JIT-Kompilierung (Just-In-Time) erzeugt optimierten Code für bestimmte Netzwerkkonfigurationen.

Je tiefer und breiter die Netzwerke werden, desto wichtiger wird die Optimierung der Vorwärtsausbreitung. Moderne Architekturen wie ResNets, Transformers und EfficientNets beinhalten Design-Entscheidungen, die die Vorwärtsausbreitung effizienter machen und gleichzeitig die Modellgenauigkeit beibehalten oder verbessern.

Im nächsten Abschnitt werden wir untersuchen, wie die Vorwärtspropagation mit der Rückwärtspropagation (Backpropagation) verbunden ist, um das Bild zu vervollständigen, wie neuronale Netze lernen.

Die Beziehung zur Backpropagation

Wir haben uns jetzt eingehend mit der Vorwärtspropagation beschäftigt, aber das ist nur die halbe Miete, wenn es um neuronale Netze geht. Schauen wir uns kurz an, wie die Vorwärtspropagation mit der Rückwärtspropagation zusammenhängt, dem Algorithmus, mit dem neuronale Netze lernen können.

Verbindung von Vorwärts- und Rückwärtsausbreitung

Vorwärtspropagation und Rückwärtspropagation ergänzen sich in neuronalen Netzen:

• Vorwärtspropagation nimmt Eingaben entgegen und erstellt Vorhersagen, indem sie sich von links nach rechts durch das Netzwerk bewegt.
• Backpropagation nimmt Fehler auf und aktualisiert die Gewichte, indem sie sich von rechts nach links durch das Netzwerk bewegt.

Diese beiden Prozesse sind untrennbar mit dem Lernprozess verbunden. Die Rückwärtspropagation kann nicht stattfinden, ohne dass vorher eine Vorwärtspropagation durchgeführt wird:

1. Die Aktivierungen aus jeder Schicht (die wir in unseren Caches gespeichert haben).
2. Die endgültige Vorhersage, die mit dem wahren Label verglichen wird.
3. Die Netzwerkarchitektur und die Gewichte, die bei der Vorwärtspropagation verwendet werden.

Stell dir vor, dass ein neuronales Netzwerk auf der Grundlage seines aktuellen Wissensstandes seine beste Vermutung anstellt, während es dieses Wissen auf der Grundlage seiner Fehler durch Backpropagation verfeinert.

Die Lernschleife

Der gesamte Lernprozess folgt einem zyklischen Muster:

1. Vorwärtsausbreitung: Das Netzwerk verarbeitet die Eingabedaten und macht Vorhersagen.
2. Verlustberechnung: Die Vorhersagen werden mit den tatsächlichen Zielen verglichen, um den Fehler zu berechnen.
3. Rückwärtsausbreitung: Der Fehler wird rückwärts durch das Netzwerk propagiert, um festzustellen, wie jedes Gewicht zu dem Fehler beigetragen hat.
4. Gewicht aktualisieren: Die Gewichte werden angepasst, um den Fehler zu reduzieren.
5. Wiederhole: Der Prozess wird mit neuen Daten fortgesetzt, bis das Netzwerk eine gute Leistung erbringt.

Das Besondere an diesem Verfahren ist, dass die Vorwärtspropagation den Kontext liefert, der für die Rückwärtspropagation benötigt wird. Bei der Vorwärtsausbreitung macht das Netzwerk nicht nur Vorhersagen, sondern behält auch alle Zwischenwerte und Entscheidungen im Auge. Die Backpropagation nutzt diese Informationen dann, um gezielte Anpassungen vorzunehmen.

Das Schöne an diesem System ist, dass aus dem Zusammenspiel dieser beiden relativ einfachen Prozesse ein komplexes Lernen entsteht. Die Vorwärtspropagation ist ganz einfach - sie besteht nur aus Matrixmultiplikationen und Aktivierungsfunktionen, die nacheinander angewendet werden. Die Backpropagation ist komplexer, ergibt sich aber direkt aus den Prinzipien der Infinitesimalrechnung.

Zusammen ermöglichen sie es neuronalen Netzen, praktisch jedes Muster zu lernen, wenn sie genügend Daten und Rechenressourcen haben. Diese Lernfähigkeit hat zu Durchbrüchen in den Bereichen Computer Vision, natürliche Sprachverarbeitung, Spiele und unzähligen anderen Bereichen geführt.

Ein gründliches Verständnis der Vorwärtspropagation, wie wir es in diesem Artikel getan haben, ist die Grundlage, um den gesamten Lernprozess in neuronalen Netzen zu verstehen. Wenn du tiefer in den Lernaspekt eintauchen möchtest, findest du in unserem Leitfaden über Backpropagation zeigt dir im Detail, wie Netzwerke aus ihren Fehlern lernen.

Fazit und nächste Schritte

Die Vorwärtspropagation ist der grundlegende Prozess, der es neuronalen Netzen ermöglicht, Eingaben in Vorhersagen umzuwandeln. Wie wir bereits herausgefunden haben, handelt es sich dabei um sequentielle Matrixmultiplikationen und Aktivierungsfunktionen, die die Daten schrittweise durch die Schichten des Netzwerks transformieren. Das Verständnis dieses Prozesses ist entscheidend, egal ob du Netzwerke von Grund auf neu implementierst, moderne Frameworks verwendest oder Fehler bei der Modellleistung behebst. 

Mit der Beherrschung von Forward Propagation hast du einen wichtigen Schritt getan, um Deep-Learning-Modelle zu erstellen und zu verstehen, mit denen du komplexe Probleme in verschiedenen Bereichen lösen kannst.

Um deine Deep Learning-Reise fortzusetzen, kannst du die umfassenden Ressourcen des DataCamps nutzen: 

• Tauche ein in die Mathematik hinter neuronalen Netzen mit Einführung in tiefe neuronale Netze
• Meistere den Trainingsprozess mit Backpropagation meistern
• Sammle praktische Erfahrungen beim Aufbau von Netzwerken in PyTorch oder R.

Für einen strukturierten Lernpfad ist das Deep Learning in Python Lernpfad bietet alles, was du brauchst, um neuronale Netze für reale Anwendungen zu entwickeln und einzusetzen.