Propagación hacia delante en redes neuronales: Guía completa

Las redes neuronales han revolucionado la inteligencia artificial, potenciándolo todo, desde el reconocimiento de imágenes hasta el procesamiento del lenguaje natural. En el corazón de estos potentes modelos se encuentra un proceso fundamental llamado propagación hacia delante. Esta guía explorará este concepto básico, llevándote desde los principios básicos hasta la aplicación práctica. 

Si buscas una guía práctica para muchos de los conceptos que cubrimos aquí, asegúrate de consultar nuestro Curso de Aprendizaje Profundo en Python.

¿Qué es la propagación hacia delante?

La propagación hacia delante es el proceso por el que una red neuronal transforma los datos de entrada en predicciones o salidas. Piensa en ella como la fase de "pensamiento" de una red neuronal: cuando se le muestra una entrada (como una imagen o un texto), la propagación hacia delante es el modo en que la red procesa esa información a través de sus capas para producir un resultado.

En términos técnicos, es el cálculo secuencial que mueve los datos desde la capa de entrada, a través de las capas ocultas, y finalmente a la capa de salida. Durante este recorrido, los datos se transforman mediante conexiones ponderadas y funciones de activación, lo que permite a la red captar patrones complejos.

Por qué es importante comprender la propagación hacia delante

Comprender la propagación hacia delante es crucial por varias razones:

1. Base para el aprendizaje: No puedes comprender cómo aprenden las redes neuronales sin entender primero cómo hacen predicciones. La propagación hacia delante es el requisito previo para comprender la retropropagaciónel algoritmo que permite el aprendizaje.
2. Depuración y optimización: Cuando las redes neuronales no funcionan bien, saber cómo fluyen los datos por la red te ayuda a identificar y solucionar los problemas.
3. Diseño del modelo: Un diseño eficaz de la arquitectura requiere comprender cómo se propaga la información a través de las distintas configuraciones de capas.
4. Eficacia del despliegue: Optimizar la propagación hacia delante es esencial para desplegar modelos en entornos con recursos limitados.

Lo que aprenderás en esta guía

Al final de esta guía exhaustiva, podrás:

• Comprender las matemáticas que hay detrás de los cálculos de las redes neuronales
• Ser capaz de implementar la propagación hacia delante desde cero utilizando NumPy
• Saber utilizar marcos modernos como TensorFlow y PyTorch para una propagación hacia delante eficiente
• Visualiza cómo se transforma la información cuando se mueve por una red
• Conectar la propagación hacia delante con el proceso de aprendizaje más amplio en las redes neuronales
• Implementa un ejemplo de trabajo completo con datos reales

Requisitos previos

Para sacar el máximo partido a esta guía, debes tener:

• Conocimientos básicos de programación en Python
• Familiaridad con conceptos matemáticos fundamentales (vectores, matrices y cálculo básico)
• Cierta exposición a conceptos de aprendizaje automático

Si necesitas reforzar tus cimientos, considera estos recursos:

• Introducción a las Redes Neuronales Profundas para los conceptos básicos.
• Introducción al Aprendizaje Profundo en Python para una experiencia de aprendizaje interactiva.
• Construir una red neuronal sencilla desde cero para practicar.

Incluso sin amplios conocimientos previos, hemos diseñado esta guía para construir los conceptos progresivamente, haciendo que las redes neuronales sean accesibles para los estudiantes decididos. ¡Vamos a sumergirnos!

Fundamentos de la propagación hacia delante

Para comprender la propagación hacia delante, tenemos que empezar por sus componentes fundamentales. Empecemos por la unidad de cálculo más pequeña de las redes neuronales y vayamos aumentando gradualmente hasta llegar a estructuras más complejas.

La neurona única: donde empieza todo

El viaje de la red neuronal comienza con un fascinante paralelismo con la biología. Al igual que el cerebro humano está formado por miles de millones de neuronas interconectadas, las redes neuronales artificiales se construyen a partir de modelos matemáticos inspirados en estas células biológicas.

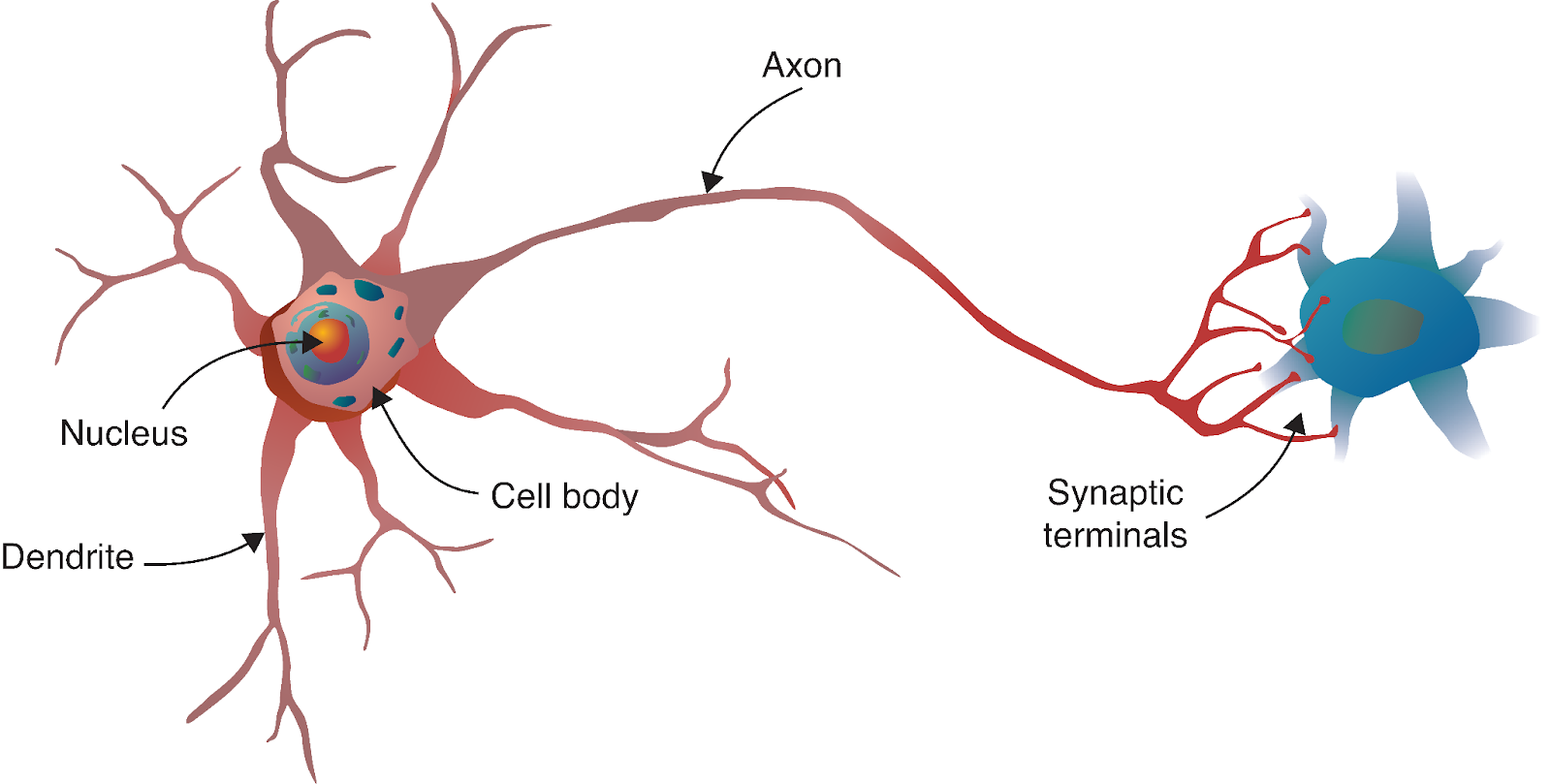
Fuente: Aprendizaje profundo - Enfoque visual

Una neurona biológica recibe señales de otras neuronas a través de las dendritas, procesa estas señales en su cuerpo celular y luego transmite el resultado a través del axón a otras neuronas. En nuestro modelo computacional, reflejamos este proceso con:

• Entradas: Las señales que llegan a la neurona (como las dendritas que reciben señales).
• Pesas: La importancia asignada a cada entrada (análoga a la fuerza de las conexiones sinápticas).
• Sesgo: Un parámetro adicional que ayuda a que la neurona se active o permanezca inactiva independientemente de las entradas.
• Función de activación: Determina si la neurona "dispara" y con qué intensidad en función de sus entradas (de forma similar al cuerpo celular que decide si genera un potencial de acción).
• Salida: La señal enviada a la capa siguiente (como el axón que transmite a otras neuronas).

Visualicemos una sola neurona para concretarlo:

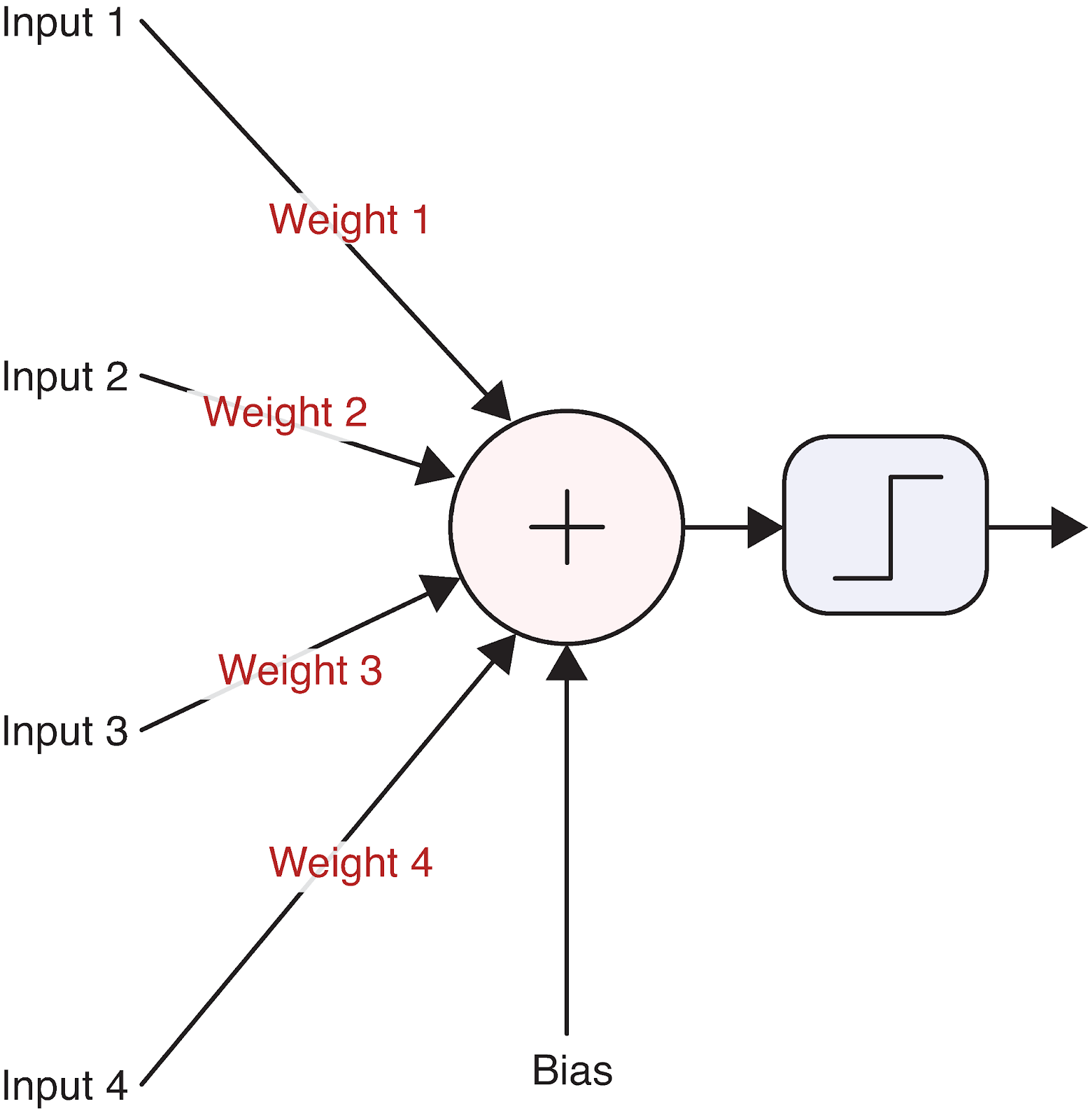
Fuente: Aprendizaje profundo - Enfoque visual

Esta sencilla unidad de cálculo constituye la base de las redes neuronales más complejas. Pero, ¿cómo transforma exactamente una neurona sus entradas en una salida? Aquí es donde entran en juego las matemáticas.

Fundamento matemático de una sola neurona

El funcionamiento de una neurona puede describirse con una ecuación sencilla:

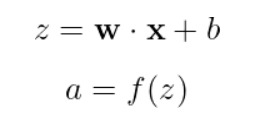
Desglosando esto:

• x es nuestro vector de entrada [x_1, x_2, x_3, ...]
• w es nuestro vector de pesos [w_1, w_2, ..., w_n].
• b es el sesgo (un único valor escalar)
• z es la suma ponderada más el sesgo (a menudo llamado "preactivación" o "logit")
• f es la función de activación
• a es la salida final de la neurona

Veamos un ejemplo concreto con números reales. Supongamos que tenemos una neurona con tres entradas:

Inputs: x = [2, 5, -1]
Weights: w = [0.5, -1, 2]
Bias: b = 0.5

En primer lugar, calculamos la suma ponderada más el sesgo:

A continuación, aplicamos una función de activación. Utilicemos la popular función ReLU (Unidad Lineal Rectificada), que se define como:

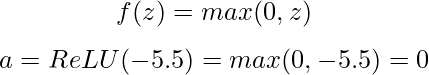
Con un valor de preactivación negativo, nuestra neurona ReLU emite 0, lo que significa que no se "dispara" para esta entrada concreta.

La función de activación es crucial porque introduce la no linealidad en la red. Sin ella, las redes neuronales se limitarían a aprender sólo relaciones lineales, independientemente del número de capas que tuvieran. Las funciones de activación habituales son

• Sigmoidea: 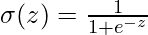Salida entre 0 y 1, útil para la clasificación binaria
• ReLU: 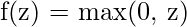Sencilla, eficaz y ayuda con el problema del gradiente evanescente
• Tanh: 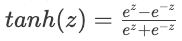- Salidas entre -1 y 1, se utiliza a menudo en capas ocultas

Cada función de activación tiene sus puntos fuertes y sus casos de uso, que exploraremos más cuando implementemos nuestra red neuronal.

De las neuronas a las capas

Las neuronas individuales son potentes, pero la verdadera fuerza de las redes neuronales surge cuando las neuronas se organizan en capas. Una capa es simplemente un conjunto de neuronas que procesan entradas en paralelo. En una red neuronal suele haber tres tipos de capas:

1. Capa de entrada: Recibe los datos brutos y los pasa a la capa siguiente
2. Capas ocultas: Procesa la información de las capas anteriores
3. Capa de salida: Produce la predicción o clasificación final

Cuando tenemos varias neuronas en una capa, cada una de las cuales recibe las mismas entradas pero con pesos y sesgos diferentes, podemos representarlo eficazmente con operaciones matriciales. Veamos cómo funciona.

Imagina que tenemos una capa con 3 valores de entrada y 4 neuronas. Cada neurona tiene su propio conjunto de pesos y sesgos:

Inputs: x = [x₁, x₂, x₃]
Weights for neuron 1: w₁ = [w₁₁, w₁₂, w₁₃]
Weights for neuron 2: w₂ = [w₂₁, w₂₂, w₂₃]
Weights for neuron 3: w₃ = [w₃₁, w₃₂, w₃₃]
Weights for neuron 4: w₄ = [w₄₁, w₄₂, w₄₃]
Biases: b = [b₁, b₂, b₃, b₄]

Podemos organizar estos pesos en una matriz W:

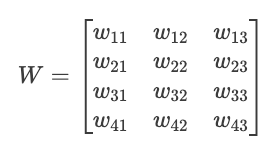
Ahora podemos calcular todas las preactivaciones neuronales a la vez con una sola multiplicación matricial:

Dónde:

• X es nuestro vector de entrada [x₁, x₂, x₃].
• W^T es la transposición de nuestra matriz de pesos
• B es nuestro vector de sesgo [b₁, b₂, b₃, b₄].
• Z es el vector resultante de las preactivaciones [z₁, z₂, z₃, z₄].

A continuación, aplicamos la función de activación elemento a elemento para obtener nuestras salidas finales:

Esta representación matricial no es sólo elegancia matemática; también es eficiencia computacional. El hardware moderno (especialmente las GPU) está optimizado para las operaciones matriciales, lo que hace que este enfoque sea mucho más rápido que calcular la salida de cada neurona individualmente.

La capacidad de apilar estas capas -convirtiendo la salida de una capa en la entrada de la siguiente- es lo que confiere a las redes neuronales su extraordinaria capacidad para aprender patrones complejos. Al conectar estos bloques de construcción, estamos preparados para explorar cómo funciona la propagación hacia delante en toda una red neuronal.

Propagación hacia delante a través de una red completa

Ahora que entendemos las neuronas individuales y las capas, demos un paso atrás y veamos cómo funciona la propagación hacia delante en toda una red neuronal. Aquí es donde surge el verdadero poder del aprendizaje profundo.

Redes multicapa: la imagen completa

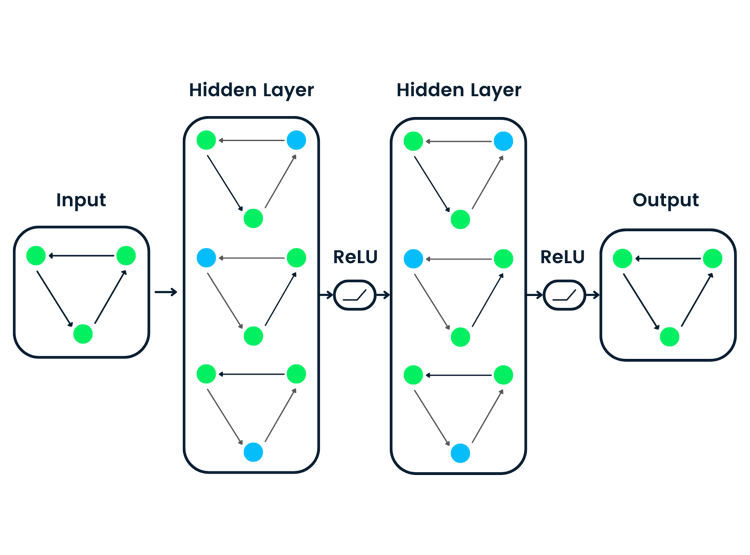
Una red neuronal completa consta de una capa de entrada, una o varias capas ocultas y una capa de salida. El término "profundo" en aprendizaje profundo se refiere a redes con múltiples capas ocultas. Cada capa transforma los datos de formas cada vez más abstractas, lo que permite a la red aprender representaciones complejas.

Consideremos una red neuronal sencilla con:

• Una capa de entrada con 4 características
• Dos capas ocultas con 3 y 2 neuronas, respectivamente
• Una capa de salida con 3 neuronas (quizás para clasificación multiclase)

Visualmente, esta red tiene el siguiente aspecto:

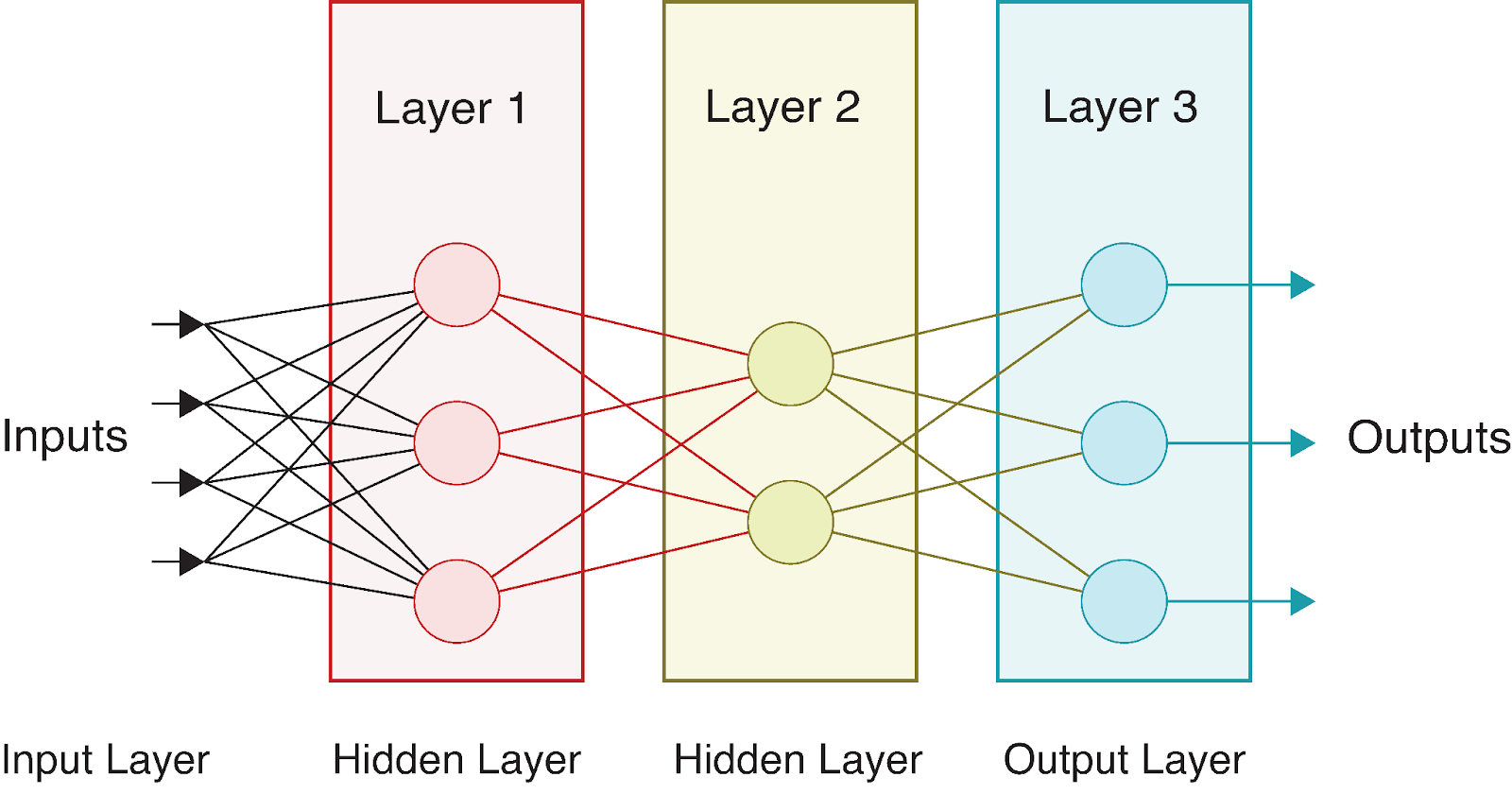
A medida que los datos fluyen por esta red, realizamos una serie de cálculos en cada capa. Si denotamos:

• Vector de entrada como X = [x_1, x_2, x_3, x_4]
• Matrices de pesos como 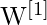(para la capa oculta) y 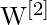(para la capa de salida)
• Vectores de sesgo como 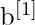y
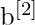
• Funciones de activación como f1 (para la capa oculta) y f2 (para la capa de salida)

Podemos expresar la propagación hacia delante a través de toda esta red como:

1. Calcula las preactivaciones de la capa oculta: 

2. Aplica la función de activación para obtener las salidas de la capa oculta: 

3. Calcula las preactivaciones de la capa de salida: 

4. Aplica la función de activación para obtener las salidas finales:

La salida final A^[2] representa la predicción de la red. Para los problemas de clasificación, pueden ser las probabilidades de cada clase; para la regresión, pueden ser los valores predichos.

Las distintas capas suelen utilizar funciones de activación diferentes. Por ejemplo, las capas ocultas suelen utilizar ReLU, mientras que las capas de salida pueden utilizar:

• Sigmoide para clasificación binaria
• Softmax para clasificación multiclase
• Lineal (sin activación) para la regresión

Lo bueno de esta estructura multicapa es que cada capa puede aprender a representar distintos aspectos de los datos. Las primeras capas suelen detectar rasgos sencillos, mientras que las capas más profundas los combinan en patrones más complejos. Este aprendizaje jerárquico es lo que hace que las redes neuronales sean tan potentes para tareas complejas como el reconocimiento de imágenes y del habla.

Algoritmo de propagación hacia delante

Formalicemos el proceso de propagación hacia delante en un algoritmo. Para una red neuronal con L capas, la propagación hacia delante sigue estos pasos:

# Pseudocode for forward propagation
def forward_propagation(X, parameters):
   """
   X: Input data (batch_size, n_features)
   parameters: Dictionary containing weights and biases for each layer
   Returns: The final output and all intermediate activations
   """
   # Store all activations for later use (e.g., in backpropagation)
   activations = {'A0': X}  # A0 is the input
  
   # Loop through L-1 layers (excluding the output layer)
   for l in range(1, L):
       # Get previous activation
       A_prev = activations[f'A{l-1}']
      
       # Get weights and biases for current layer
       W = parameters[f'W{l}']
       b = parameters[f'b{l}']
      
       # Compute pre-activation
       Z = np.dot(A_prev, W.T) + b
      
       # Apply activation function (e.g., ReLU for hidden layers)
       A = relu(Z)
      
       # Store values for later use
       activations[f'Z{l}'] = Z
       activations[f'A{l}'] = A
  
   # Compute output layer (layer L)
   A_prev = activations[f'A{L-1}']
   W = parameters[f'W{L}']
   b = parameters[f'b{L}']
  
   # Compute pre-activation for output layer
   Z = np.dot(A_prev, W.T) + b
  
   # Apply output activation function (depends on the task)
   if task == 'binary_classification':
       A = sigmoid(Z)
   elif task == 'multiclass_classification':
       A = softmax(Z)
   elif task == 'regression':
       A = Z  # Linear activation
  
   # Store output layer values
   activations[f'Z{L}'] = Z
   activations[f'A{L}'] = A
  
   return A, activations

Este algoritmo pone de relieve varios aspectos importantes de la propagación hacia delante:

1. Procesamiento secuencial: La información fluye estrictamente hacia delante, capa por capa.
2. Almacenamiento de activación: Almacenamos no sólo la salida final, sino todas las activaciones intermedias, que serán cruciales para entrenar la red mediante retropropagación.
3. Salida específica de la tarea: La función de activación de la capa de salida se elige en función del problema concreto (clasificación frente a regresión).

El algoritmo de propagación hacia delante es extraordinariamente sencillo, pero permite a las redes neuronales aproximar funciones increíblemente complejas. Cuando se combina con un entrenamiento adecuado mediante retropropagación, este sencillo proceso permite a la red aprender de los datos y hacer predicciones cada vez más precisas.

Veamos un ejemplo concreto para comprenderlo mejor. Considera que la entrada X = [0,5, -0,2, 0,1] pasa por nuestra red de ejemplo con:

• Pesos de la capa oculta W^[1] (matriz de 4×3) y sesgos b^[1] (vector de 4 valores)
• Pesos de la capa de salida W^[2] (matriz de 2×4) y sesgos b^[2] (vector de 2 valores)

Para simplificar, digamos que todas las ponderaciones son 0,1 y todos los sesgos son 0:

X = [0.5, -0.2, 0.1]
W[1] = [[0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1]]
b[1] = [0, 0, 0, 0]
W[2] = [[0.1, 0.1, 0.1, 0.1], [0.1, 0.1, 0.1, 0.1]]
b[2] = [0, 0]

Siguiendo nuestro algoritmo:

• Primer paso:

• Segundo paso con ReLU: 

• Tercer paso:

• Cuarto paso con el uso de la sigmoidea: 

Esto nos da nuestra predicción final. En un contexto de clasificación binaria, estos valores cercanos a 0,5 indicarían incertidumbre entre las dos clases.

En la siguiente sección, pondremos en práctica la propagación hacia delante en Python para ver estos cálculos en acción.

Implementación de la propagación hacia delante en Python

Ahora que entendemos la teoría de la propagación hacia delante, vamos a ponerla en práctica implementándola en Python. Empezaremos con una implementación "desde cero" utilizando sólo NumPy, y luego veremos cómo los modernos marcos de aprendizaje profundo simplifican este proceso.

Construir desde cero con NumPy

NumPy proporciona operaciones eficientes con matrices que nos permiten realizar los cálculos matriciales de los que hemos hablado. Vamos a construir una clase de red neuronal sencilla que realice propagación hacia delante a través de varias capas.

En primer lugar, tendremos que importar las bibliotecas necesarias:

import numpy as np
import matplotlib.pyplot as plt

# For reproducibility
np.random.seed(42)

Ahora vamos a definir las funciones de activación que utilizaremos en nuestra red:

def relu(Z):
   """ReLU activation function: max(0, Z)"""
   return np.maximum(0, Z)

def sigmoid(Z):
   """Sigmoid activation function: 1/(1 + e^(-Z))"""
   return 1 / (1 + np.exp(-Z))

def softmax(Z):
   """Softmax activation function for multi-class classification"""
   # Subtract max for numerical stability (prevents overflow)
   exp_Z = np.exp(Z - np.max(Z, axis=1, keepdims=True))
   return exp_Z / np.sum(exp_Z, axis=1, keepdims=True)

A continuación, vamos a crear una clase para nuestra red neuronal:

class NeuralNetwork:
   def __init__(self, layer_dims, activations):
       """
       Initialize a neural network with specified layer dimensions and activations
      
       Parameters:
       - layer_dims: List of integers representing the number of neurons in each layer
                    (including input and output layers)
       - activations: List of activation functions for each layer (excluding input layer)
       """
       self.L = len(layer_dims) - 1  # Number of layers (excluding input layer)
       self.layer_dims = layer_dims
       self.activations = activations
       self.parameters = {}
      
       # Initialize parameters (weights and biases)
       self.initialize_parameters()
  
   def initialize_parameters(self):
       """Initialize weights and biases with small random values"""
       for l in range(1, self.L + 1):
           # He initialization for weights - helps with training deep networks
           self.parameters[f'W{l}'] = np.random.randn(self.layer_dims[l], self.layer_dims[l-1]) * np.sqrt(2 / self.layer_dims[l-1])
           self.parameters[f'b{l}'] = np.zeros((self.layer_dims[l], 1))
  
   def forward_propagation(self, X):
       """
       Perform forward propagation through the network
      
       Parameters:
       - X: Input data (n_features, batch_size)
      
       Returns:
       - AL: Output of the network
       - caches: Dictionary containing all activations and pre-activations
       """
       caches = {}
       A = X  # Input layer activation
       caches['A0'] = X
      
       # Process through L-1 layers (excluding output layer)
       for l in range(1, self.L):
           A_prev = A
          
           # Get weights and biases for current layer
           W = self.parameters[f'W{l}']
           b = self.parameters[f'b{l}']
          
           # Forward propagation for current layer
           Z = np.dot(W, A_prev) + b
          
           # Apply activation function
           activation_function = self.activations[l-1]
           if activation_function == "relu":
               A = relu(Z)
           elif activation_function == "sigmoid":
               A = sigmoid(Z)
          
           # Store values for backpropagation
           caches[f'Z{l}'] = Z
           caches[f'A{l}'] = A
      
       # Output layer
       W = self.parameters[f'W{self.L}']
       b = self.parameters[f'b{self.L}']
       Z = np.dot(W, A) + b
      
       # Apply output activation function
       activation_function = self.activations[self.L-1]
       if activation_function == "sigmoid":
           AL = sigmoid(Z)
       elif activation_function == "softmax":
           AL = softmax(Z)
       elif activation_function == "linear":
           AL = Z  # No activation for regression
      
       # Store output layer values
       caches[f'Z{self.L}'] = Z
       caches[f'A{self.L}'] = AL
      
       return AL, caches

La clase NeuralNetwork que hemos implementado anteriormente proporciona un marco completo para crear y utilizar una red neuronal con arquitectura personalizable. Vamos a desglosar sus componentes clave:

1. Inicialización: La red se configura con las dimensiones de capa y las funciones de activación especificadas. Inicializa automáticamente los pesos y los sesgos utilizando el método de inicialización He para mejorar el rendimiento del entrenamiento.
2. Propagación hacia delante: El método forward_propagation que acabamos de implementar es el corazón de la capacidad de predicción de la red neuronal. Ello:

• Toma los datos de entrada y los pasa por cada capa
• Aplica la función de activación adecuada en cada capa
• Almacena valores intermedios en cachés para utilizarlos posteriormente en la retropropagación
• Devuelve tanto el resultado final como todos los valores almacenados en caché

3. Funciones de activación: La red admite múltiples funciones de activación, como ReLU, sigmoide y softmax, lo que le permite manejar distintos tipos de problemas (regresión o clasificación).

4. Arquitectura flexible: La implementación permite redes de profundidad y anchura arbitrarias, lo que la hace adecuada para una amplia gama de tareas de aprendizaje automático.

Esta implementación sigue el patrón estándar de diseño de redes neuronales, en el que los datos fluyen hacia delante a través de la red, y cada capa transforma los datos antes de pasarlos a la capa siguiente.

Ahora vamos a probar nuestra aplicación con una pequeña red de ejemplo:

# Create a sample network
# Input layer: 3 features
# Hidden layer 1: 4 neurons with ReLU activation
# Output layer: 2 neurons with sigmoid activation (binary classification)
layer_dims = [3, 4, 2]
activations = ["relu", "sigmoid"]
nn = NeuralNetwork(layer_dims, activations)

# Create sample input data - 3 features for 5 examples
X = np.random.randn(3, 5)

# Perform forward propagation
output, caches = nn.forward_propagation(X)

print(f"Input shape: {X.shape}")
print(f"Output shape: {output.shape}")
print(f"Output values:\n{output}")

Salida:

Input shape: (3, 5)
Output shape: (2, 5)
Output values:
[[0.00386784 0.54343014 0.39661893 0.5        0.51056934]
[0.11877049 0.32541093 0.44840699 0.5        0.45586633]]

Visualicemos también cómo se transforman los datos a medida que fluyen por la red:

def visualize_activations(caches, example_idx=0):
   """Visualize the activations for a single example through the network"""
   plt.figure(figsize=(15, 6))
  
   # Plot input
   plt.subplot(1, 3, 1)
   plt.bar(range(caches['A0'].shape[0]), caches['A0'][:, example_idx])
   plt.title('Input Layer')
   plt.xlabel('Feature')
   plt.ylabel('Value')
  
   # Plot hidden layer activation
   plt.subplot(1, 3, 2)
   plt.bar(range(caches['A1'].shape[0]), caches['A1'][:, example_idx])
   plt.title('Hidden Layer (ReLU Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   # Plot output layer
   plt.subplot(1, 3, 3)
   plt.bar(range(caches['A2'].shape[0]), caches['A2'][:, example_idx])
   plt.title('Output Layer (Sigmoid Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   plt.tight_layout()
   plt.show()

# Visualize the first example
visualize_activations(caches)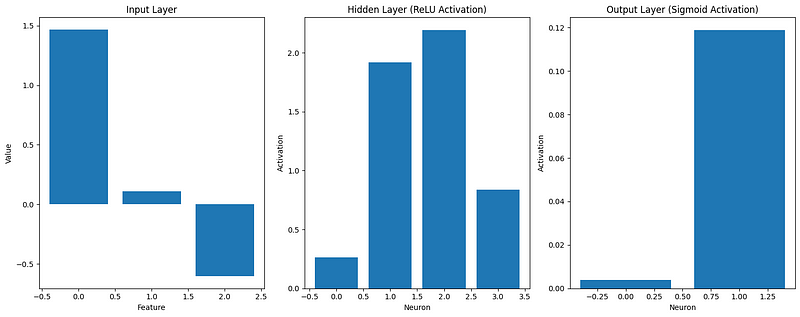

Esta visualización nos ayuda a comprender cómo se transforman los datos de entrada a medida que se propagan por la red. Podemos verlo:

1. Las características de entrada pueden tener valores positivos o negativos
2. Tras la activación ReLU en la capa oculta, todas las activaciones son no negativas
3. La activación sigmoidea en la capa de salida restringe los valores entre 0 y 1

Nuestra implementación "desde cero" demuestra los principios básicos de la propagación hacia delante, pero los marcos modernos de aprendizaje profundo proporcionan herramientas más eficientes y flexibles para construir redes neuronales.

Utilizar marcos de aprendizaje profundo

Ahora, implementemos la misma red neuronal utilizando marcos de aprendizaje profundo populares: TensorFlow y PyTorch. Estos marcos optimizan el rendimiento y proporcionan abstracciones de alto nivel, facilitando la construcción de modelos complejos.

En primer lugar, veamos la implementación de TensorFlow/Keras:

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Input

# For reproducibility
tf.random.set_seed(42)

# Create the same network architecture
tf_model = Sequential([
   Input(shape=(3,)),  # Input layer with 3 features
   Dense(4, activation='relu'),  # Hidden layer with 4 neurons
   Dense(2, activation='sigmoid')  # Output layer with 2 neurons
])

tf_model.summary()

# Sample input data with the shape expected by Keras
X_tf = np.random.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in TensorFlow
tf_output = tf_model.predict(X_tf)

print(f"TensorFlow output shape: {tf_output.shape}")
print(f"TensorFlow output values:\n{tf_output}")

TensorFlow output shape: (5, 2)
TensorFlow output values:
[[0.6855308  0.7139542 ]
[0.4952355  0.5231934 ]
[0.50174904 0.5198488 ]
[0.44331825 0.6860926 ]
[0.6624589  0.5385444 ]]

Acabamos de implementar nuestra red neuronal utilizando TensorFlow/Keras y hemos realizado con éxito la propagación hacia delante en algunos datos de muestra. El resumen del modelo muestra nuestra arquitectura con una capa de entrada que acepta 3 características, una capa oculta con 4 neuronas que utilizan activación ReLU y una capa de salida con 2 neuronas que utilizan activación sigmoidea. En total, el modelo tiene 26 parámetros entrenables.

Los resultados de la propagación hacia delante muestran la forma de salida (5, 2) correspondiente a nuestros 5 ejemplos de entrada, cada uno de los cuales produce 2 valores de salida. Estas salidas están limitadas entre 0 y 1 debido a la función de activación sigmoidea de la capa de salida.

A continuación, veamos cómo podemos implementar la misma arquitectura de red neuronal utilizando PyTorch, otro popular marco de aprendizaje profundo, para comparar los enfoques.

import torch
import torch.nn as nn

# For reproducibility
torch.manual_seed(42)

# Create a network in PyTorch
class PyTorchNN(nn.Module):
   def __init__(self):
       super(PyTorchNN, self).__init__()
       self.hidden = nn.Linear(3, 4)  # 3 inputs, 4 hidden neurons
       self.relu = nn.ReLU()
       self.output = nn.Linear(4, 2)  # 4 inputs from hidden, 2 outputs
       self.sigmoid = nn.Sigmoid()
  
   def forward(self, x):
       x = self.relu(self.hidden(x))
       x = self.sigmoid(self.output(x))
       return x

# Instantiate the model
torch_model = PyTorchNN()

# Print model structure
print(torch_model)

Salida:

PyTorchNN(
 (hidden): Linear(in_features=3, out_features=4, bias=True)
 (relu): ReLU()
 (output): Linear(in_features=4, out_features=2, bias=True)
 (sigmoid): Sigmoid()
)

```python
# Sample input data
X_torch = torch.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in PyTorch
torch_output = torch_model(X_torch)

print(f"PyTorch output shape: {torch_output.shape}")
print(f"PyTorch output values:\n{torch_output}")

Salida:

PyTorch output shape: torch.Size([5, 2])
PyTorch output values:
tensor([[0.4516, 0.4116],
       [0.4289, 0.4267],
       [0.4278, 0.4172],
       [0.3771, 0.4321],
       [0.5769, 0.3328]], grad_fn=<SigmoidBackward0>)

Comparemos nuestras implementaciones:

# Compare dimensions and structure of outputs
print("\nComparison of implementations:")
print(f"NumPy output shape: {output.shape}")
print(f"TensorFlow output shape: {tf_output.shape}")
print(f"PyTorch output shape: {torch_output.shape}")

Salida:

Comparison of implementations:
NumPy output shape: (2, 5)
TensorFlow output shape: (5, 2)
PyTorch output shape: torch.Size([5, 2])

Las diferencias clave entre nuestras implementaciones:

1. Estructura y legibilidad:

• NumPy: La implementación explícita de cada paso proporciona un control y una transparencia completos
• TensorFlow/Keras: Las abstracciones de alto nivel ocultan los detalles de implementación, pero simplifican el código
• PyTorch: Enfoque orientado a objetos con método de avance explícito

2. Rendimiento:

• TensorFlow y PyTorch optimizan las operaciones para la aceleración en la GPU
• Ambos marcos implementan un cálculo de gradiente eficiente para el entrenamiento
• Los marcos optimizan el uso de memoria para redes grandes

3. Extensibilidad:

• Los marcos proporcionan componentes preconstruidos (capas, optimizadores, etc.)
• Herramientas integradas para guardar/cargar modelos, visualización y despliegue
• Amplio apoyo y documentación de la comunidad

Para redes sencillas, nuestra implementación NumPy funciona bien, pero a medida que aumenta la complejidad, los marcos de aprendizaje profundo se vuelven esenciales. Se encargan de las optimizaciones de bajo nivel y proporcionan herramientas para todo el flujo de trabajo del aprendizaje automático, desde el desarrollo hasta la implantación. Para saber más sobre estos marcos, consulta nuestras guías separadas:

• Tutorial de PyTorch: Construir una red neuronal sencilla desde cero
• Tutorial de TensorFlow para principiantes 

En la siguiente sección, construiremos un ejemplo de trabajo completo que aplique la propagación hacia delante a un problema del mundo real.

Ejemplo de propagación hacia delante

Ahora que hemos implementado la propagación hacia delante tanto desde cero como utilizando marcos de trabajo populares, veámosla en acción en un problema del mundo real. Construiremos un ejemplo completo y exploraremos cómo optimizar el proceso para mejorar el rendimiento.

Ejemplo práctico completo

Apliquemos nuestros conocimientos a un problema clásico de aprendizaje automático: el reconocimiento de dígitos manuscritos utilizando el conjunto de datos MNIST. Este conjunto de datos contiene 70.000 imágenes de dígitos manuscritos (0-9), cada una de 28x28 píxeles de tamaño.

Primero, vamos a cargar y preparar los datos:

from tensorflow.keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt

# Load MNIST dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# Normalize pixel values to range [0, 1]
X_train = X_train / 255.0
X_test = X_test / 255.0

# Reshape images to vectors (flatten 28x28 to 784)
X_train_flat = X_train.reshape(X_train.shape[0], -1).T  # Shape: (784, 60000)
X_test_flat = X_test.reshape(X_test.shape[0], -1).T     # Shape: (784, 10000)

# Convert labels to one-hot encoding
def one_hot_encode(y, num_classes=10):
   one_hot = np.zeros((num_classes, y.size))
   one_hot[y, np.arange(y.size)] = 1
   return one_hot

y_train_one_hot = one_hot_encode(y_train)  # Shape: (10, 60000)
y_test_one_hot = one_hot_encode(y_test)    # Shape: (10, 10000)

# Display sample images
plt.figure(figsize=(10, 5))
for i in range(5):
   plt.subplot(1, 5, i+1)
   plt.imshow(X_train[i], cmap='gray')
   plt.title(f"Label: {y_train[i]}")
   plt.axis('off')
plt.tight_layout()
plt.show()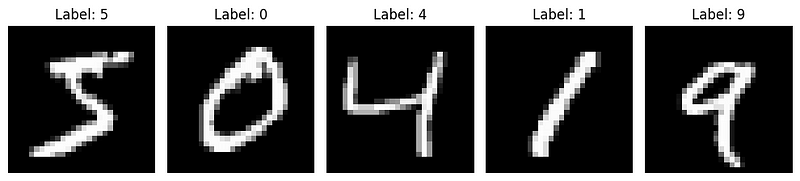

Ahora, vamos a construir una red neuronal para esta tarea utilizando nuestra implementación NumPy. Crearemos una red con:

• Capa de entrada: 784 neuronas (28x28 píxeles)
• Capa oculta: 128 neuronas con activación ReLU
• Capa de salida: 10 neuronas con activación softmax (para 10 dígitos)

# Define our network architecture
layer_dims = [784, 128, 10]
activations = ["relu", "softmax"]
nn = NeuralNetwork(layer_dims, activations)

# Take a small batch for demonstration
batch_size = 64
batch_indices = np.random.choice(X_train_flat.shape[1], batch_size, replace=False)
X_batch = X_train_flat[:, batch_indices]
y_batch = y_train_one_hot[:, batch_indices]

# Perform forward propagation
output, caches = nn.forward_propagation(X_batch)

# Compute accuracy
predictions = np.argmax(output, axis=0)
true_labels = np.argmax(y_batch, axis=0)
accuracy = np.mean(predictions == true_labels)

print(f"Batch accuracy: {accuracy:.4f}")

Out: Batch accuracy: 0.0781

Tenemos un 7% de precisión, que es peor incluso que un modelo de adivinación aleatoria. Pero eso es de esperar, ya que sólo realizamos la propagación hacia delante, no hay aprendizaje.

Ahora, visualicemos cómo la red procesa una sola imagen a través de cada capa:

def visualize_network_processing(nn, image, label, caches):
   """Visualize network processing for a single image"""
   plt.figure(figsize=(15, 10))
  
   # Plot original image
   plt.subplot(2, 3, 1)
   plt.imshow(image.reshape(28, 28), cmap='gray')
   plt.title(f"Input Image (Digit: {label})")
   plt.axis('off')
  
   # Plot flattened input (first 100 values)
   plt.subplot(2, 3, 2)
   plt.bar(range(100), image.flatten()[:100])
   plt.title("Input Layer (first 100 pixels)")
   plt.xlabel("Pixel Index")
   plt.ylabel("Pixel Value")
  
   # Plot hidden layer activations (first 50 neurons)
   plt.subplot(2, 3, 3)
   hidden_activations = caches['A1'][:50, 0]
   plt.bar(range(len(hidden_activations)), hidden_activations)
   plt.title("Hidden Layer Activations (first 50 neurons)")
   plt.xlabel("Neuron Index")
   plt.ylabel("Activation")
  
   # Plot output layer activations
   plt.subplot(2, 3, 4)
   output_activations = caches['A2'][:, 0]
   plt.bar(range(10), output_activations)
   plt.xticks(range(10))
   plt.title("Output Layer Activations (Softmax)")
   plt.xlabel("Digit Class")
   plt.ylabel("Probability")
  
   # Plot prediction vs actual
   plt.subplot(2, 3, 5)
   prediction = np.argmax(output_activations)
   plt.bar(['Actual', 'Predicted'], [label, prediction], color=['blue', 'orange'])
   plt.title(f"Prediction: {prediction}, Actual: {label}")
   plt.ylabel("Digit")
  
   plt.tight_layout()
   plt.show()

# Visualize forward propagation for the first image in our batch
image_idx = 0
image = X_batch[:, image_idx].reshape(784, 1)
label = true_labels[image_idx]

visualize_network_processing(nn, image, label, caches)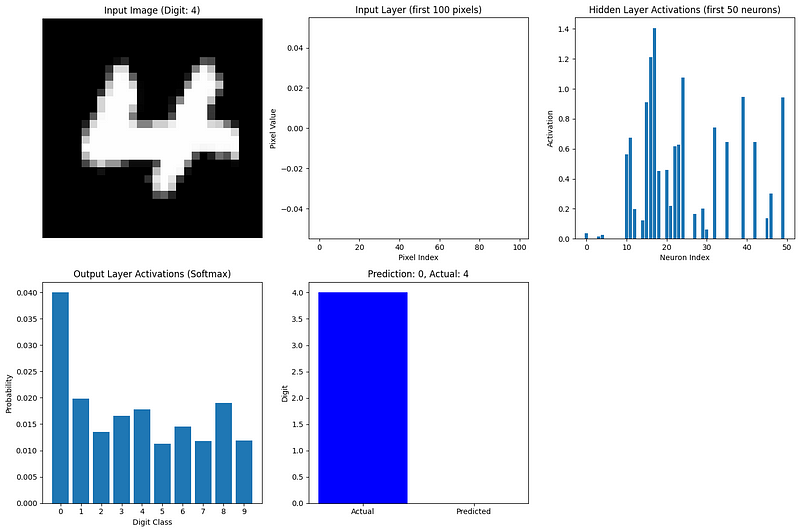

Esta visualización muestra cómo fluye la información a través de nuestra red:

1. Capa de entrada: Los píxeles aplanados de la imagen (valores entre 0 y 1)
2. Capa oculta: Las neuronas activadas por ReLU captan diferentes características del dígito
3. Capa de salida: La activación softmax da una distribución de probabilidad sobre los 10 dígitos posibles

La neurona de salida más activa corresponde a la predicción de la red. Incluso con pesos aleatorios (ya que aún no hemos entrenado la red), podemos ver cómo la propagación hacia delante transforma los datos de entrada en una predicción.

Para un ejemplo más completo, entrenaríamos esta red utilizando la retropropagación para ajustar los pesos y los sesgos, mejorando las predicciones con el tiempo. Sin embargo, incluso sin entrenamiento, este ejemplo demuestra el proceso de propagación hacia delante en datos reales.

Optimizar la propagación hacia delante

A medida que las redes neuronales crecen y los conjuntos de datos se hacen más masivos, la optimización de la propagación hacia delante se vuelve crucial. Aquí tienes estrategias clave para hacer más eficaz la propagación hacia delante:

1. Tratamiento por lotes

En lugar de procesar un ejemplo cada vez, calculamos la propagación hacia delante en lotes de ejemplos simultáneamente. Esto aprovecha las capacidades de procesamiento paralelo del hardware moderno.

2. Vectorización

Utilizar operaciones matriciales en lugar de bucles acelera drásticamente el cálculo. Por eso nuestra implementación utilizaba las operaciones de matriz de NumPy.

3. Gestión de la memoria

Para redes grandes, hay que tener cuidado con el uso de la memoria. Las técnicas incluyen:

• Reutilización de la memoria para activaciones intermedias.
• Calcula las activaciones capa por capa sin almacenar todas las intermedias.
• Utilizar representaciones de menor precisión (por ejemplo, flotantes de 16 bits en lugar de 32 bits).

4. Aceleración GPU

Las Unidades de Procesamiento Gráfico destacan en las operaciones matriciales. Los marcos de trabajo modernos pueden trasladar sin problemas el cálculo a las GPU para aumentar considerablemente la velocidad:

# TensorFlow example of GPU acceleration
import tensorflow as tf

# Check for available GPUs
print("GPUs Available:", tf.config.list_physical_devices('GPU'))

# TensorFlow automatically uses available GPUs
with tf.device('/GPU:0'):  # Explicitly specify GPU if multiple are available
   # Computation runs on GPU if available
   result = tf_model.predict(X_tf)

5. Hardware especializado

Más allá de las GPU, hardware como las Unidades de Procesamiento Tensorial (TPU) de Google están específicamente diseñadas para operaciones de redes neuronales.

6. Optimizaciones algorítmicas

Determinadas funciones de activación y arquitecturas de red están diseñadas para la eficiencia computacional:

• ReLU es más rápido de calcular que sigmoide o tanh.
• Las convoluciones separables en profundidad reducen el cálculo en comparación con las convoluciones estándar.
• La poda de la red elimina las conexiones innecesarias, reduciendo el cálculo.

7. Optimizaciones del marco

Los marcos de aprendizaje profundo implementan numerosas optimizaciones de bajo nivel:

• Las operaciones fusionadas combinan varios pasos en núcleos optimizados.
• Los algoritmos autoajustados seleccionan la implementación más rápida para un hardware específico.
• La compilación JIT (Just-In-Time) crea código optimizado para configuraciones de red específicas.

A medida que las redes se hacen más profundas y anchas, la optimización de la propagación hacia delante es cada vez más importante. Las arquitecturas modernas, como ResNets, Transformers y EfficientNets, incorporan opciones de diseño específicas para que la propagación hacia delante sea más eficiente, manteniendo o mejorando la precisión del modelo.

En la siguiente sección, exploraremos cómo la propagación hacia delante se conecta con la propagación hacia atrás (retropropagación), completando la imagen de cómo aprenden las redes neuronales.

La relación con la retropropagación

Ya hemos explorado a fondo la propagación hacia delante, pero esto es sólo la mitad de la historia cuando se trata de redes neuronales. Examinemos brevemente cómo la propagación hacia delante conecta con la retropropagación, el algoritmo que permite a las redes neuronales aprender.

Conectar la propagación hacia delante y hacia atrás

La propagación hacia delante y la retropropagación funcionan como procesos complementarios en las redes neuronales:

• Propagación hacia delante toma entradas y produce predicciones, moviéndose de izquierda a derecha a través de la red.
• Retropropagación toma los errores y produce actualizaciones de peso, moviéndose de derecha a izquierda a través de la red.

Estos dos procesos son inseparables en el proceso de aprendizaje. La retropropagación no puede producirse sin realizar antes la propagación hacia delante, como necesita:

1. Las activaciones de cada capa (que almacenamos en nuestras cachés).
2. La predicción final para comparar con la etiqueta verdadera.
3. La arquitectura de la red y los pesos utilizados durante la propagación hacia delante.

Piensa en la propagación hacia delante como una red neuronal que hace su mejor suposición, dada su comprensión actual, mientras que la retropropagación es cómo refina esa comprensión basándose en sus errores.

El bucle de aprendizaje

Todo el proceso de aprendizaje sigue un patrón cíclico:

1. Propagación hacia delante: La red procesa los datos de entrada y hace predicciones.
2. Cálculo de pérdidas: Las predicciones se comparan con los objetivos reales para calcular el error.
3. Propagación hacia atrás: El error se propaga hacia atrás por la red para determinar cómo ha contribuido cada peso al error.
4. Actualización del peso: Los pesos se ajustan para reducir el error.
5. Repite: El proceso continúa con nuevos datos hasta que la red funcione bien.

Lo que hace que este proceso sea potente es que la propagación hacia delante proporciona el contexto necesario para la retropropagación. Durante la propagación hacia delante, la red no sólo hace predicciones, sino que también lleva un registro de todos los valores y decisiones intermedios. A continuación, la retropropagación utiliza esta información para realizar ajustes específicos.

La belleza de este sistema es que el aprendizaje complejo surge de estos dos procesos relativamente sencillos que trabajan juntos. La propagación hacia delante es sencilla: sólo son multiplicaciones de matrices y funciones de activación aplicadas secuencialmente. La retropropagación es más compleja, pero se deriva directamente de los principios del cálculo.

Juntos, permiten a las redes neuronales aprender prácticamente cualquier patrón si se les proporcionan suficientes datos y recursos informáticos. Esta capacidad de aprendizaje ha impulsado avances en la visión por ordenador, el procesamiento del lenguaje natural, los juegos y otros innumerables dominios.

Comprender a fondo la propagación hacia delante, como hemos hecho en este artículo, proporciona la base necesaria para comprender el proceso completo de aprendizaje en las redes neuronales. Si te interesa profundizar en el aspecto del aprendizaje, nuestra guía sobre retropropagación proporciona una exploración detallada de cómo las redes aprenden de sus errores.

Conclusión y próximos pasos

La propagación hacia delante es el proceso fundacional que permite a las redes neuronales transformar las entradas en predicciones. Como hemos explorado, implica multiplicaciones secuenciales de matrices y funciones de activación que transforman progresivamente los datos a través de las capas de la red. Comprender este proceso es crucial tanto si estás implementando redes desde cero, como si utilizas marcos modernos o solucionas problemas de rendimiento de modelos. 

Al dominar la propagación hacia delante, habrás dado un paso importante hacia la construcción y comprensión de modelos de aprendizaje profundo que puedan abordar problemas complejos en todos los dominios.

Para continuar tu viaje de aprendizaje profundo, explora los completos recursos de DataCamp: 

• Sumérgete en las matemáticas que hay detrás de las redes neuronales con Introducción a las redes neuronales profundas
• Domina el proceso de entrenamiento con Dominar la retropropagación
• Adquiere experiencia práctica construyendo redes en PyTorch o R.

Para un camino de aprendizaje estructurado, el Aprendizaje profundo en Python te proporciona todo lo que necesitas para dominar la creación y el despliegue de redes neuronales para aplicaciones del mundo real.