Propagation vers l'avant dans les réseaux neuronaux : Un guide complet

Les réseaux neuronaux ont révolutionné l'intelligence artificielle, alimentant tout ce qui va de la reconnaissance d'images au traitement du langage naturel. Au cœur de ces modèles puissants se trouve un processus fondamental appelé propagation vers l'avant. Ce guide explore ce concept de base et vous emmène des principes fondamentaux à la mise en œuvre pratique. 

Si vous êtes à la recherche d'un guide pratique sur la plupart des concepts que nous abordons ici, n'hésitez pas à consulter notre parcours de compétences sur le Parcours de compétences sur l'apprentissage profond en Python.

Qu'est-ce que la propagation vers l'avant ?

La propagation vers l'avant est le processus par lequel un réseau neuronal transforme les données d'entrée en prédictions ou en sorties. Considérez-la comme la phase de "réflexion" d'un réseau neuronal - lorsqu'on lui présente une entrée (comme une image ou un texte), la propagation vers l'avant est la manière dont le réseau traite cette information à travers ses couches pour produire un résultat.

En termes techniques, il s'agit du calcul séquentiel qui déplace les données de la couche d'entrée à la couche de sortie en passant par les couches cachées. Au cours de ce voyage, les données sont transformées par des connexions pondérées et des fonctions d'activation, ce qui permet au réseau de saisir des modèles complexes.

Pourquoi il est important de comprendre la propagation vers l'avant

Il est essentiel de comprendre la propagation vers l'avant pour plusieurs raisons :

1. Fondation pour l'apprentissage: Vous ne pouvez pas comprendre comment les réseaux neuronaux apprennent sans d'abord comprendre comment ils font des prédictions. La propagation vers l'avant est la condition préalable à la compréhension de la rétropropagationl'algorithme qui permet l'apprentissage.
2. Débogage et optimisation: Lorsque les réseaux neuronaux ne fonctionnent pas correctement, le fait de savoir comment les données circulent dans le réseau vous permet d'identifier et de résoudre les problèmes.
3. Modèle de conception: Pour concevoir une architecture efficace, il faut comprendre comment l'information se propage à travers les différentes configurations de couches.
4. Efficacité du déploiement: L'optimisation de la propagation vers l'avant est essentielle pour le déploiement de modèles dans des environnements où les ressources sont limitées.

Ce que vous apprendrez dans ce guide

À la fin de ce guide complet, vous pourrez :

• Comprendre les mathématiques qui sous-tendent les calculs des réseaux neuronaux
• Être capable d'implémenter la propagation vers l'avant à partir de zéro en utilisant NumPy
• Savoir comment utiliser des frameworks modernes comme TensorFlow et PyTorch pour une propagation efficace.
• Visualiser comment l'information se transforme au fur et à mesure qu'elle circule dans un réseau
• Relier la propagation vers l'avant au processus d'apprentissage plus large dans les réseaux neuronaux
• Mettre en œuvre un exemple complet sur des données réelles

Conditions préalables

Pour tirer le meilleur parti de ce guide, vous devez avoir :

• Compréhension de base de la programmation Python
• Familiarité avec les concepts mathématiques fondamentaux (vecteurs, matrices et calculs de base).
• Une certaine exposition aux concepts d'apprentissage automatique

Si vous avez besoin de renforcer vos fondations, pensez à ces ressources :

• Introduction aux réseaux neuronaux profonds pour les concepts de base.
• Introduction à l'apprentissage profond en Python pour une expérience d'apprentissage interactive.
• Construire un réseau neuronal simple à partir de zéro pour une mise en pratique.

Même sans connaissances approfondies, nous avons conçu ce guide de manière à ce que les concepts soient abordés progressivement, afin de rendre les réseaux neuronaux accessibles aux apprenants déterminés. Plongeons dans l'aventure !

Fondements de la propagation vers l'avant

Pour comprendre la propagation vers l'avant, nous devons commencer par ses éléments fondamentaux. Commençons par la plus petite unité de calcul, les réseaux neuronaux, et passons progressivement à des structures plus complexes.

Le neurone unique : là où tout commence

Le voyage du réseau neuronal commence par un parallèle fascinant avec la biologie. Tout comme le cerveau humain est constitué de milliards de neurones interconnectés, les réseaux neuronaux artificiels sont construits à partir de modèles mathématiques inspirés de ces cellules biologiques.

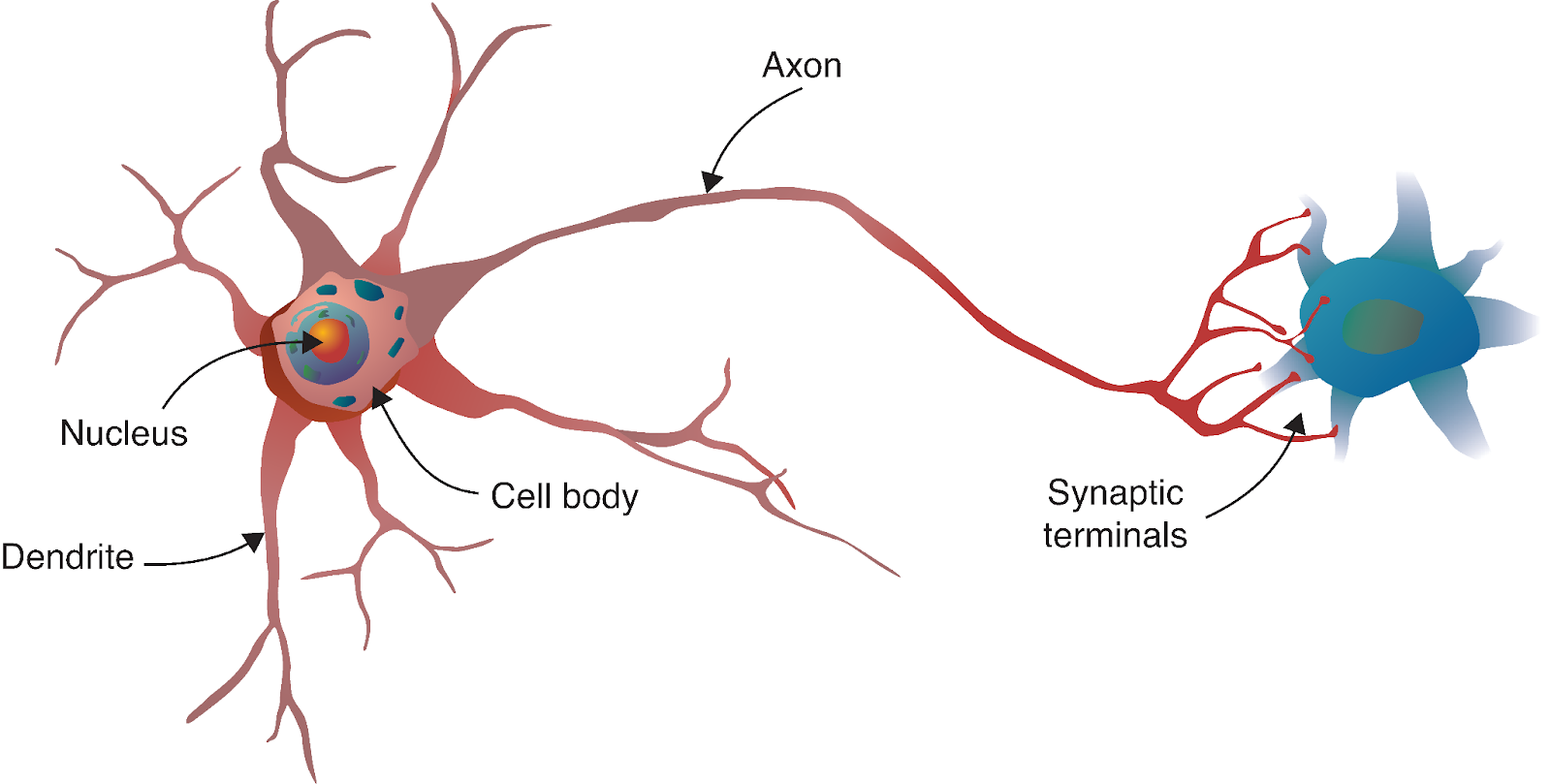
Source : Apprentissage profond - Approche visuelle

Un neurone biologique reçoit des signaux d'autres neurones par l'intermédiaire des dendrites, traite ces signaux dans son corps cellulaire, puis transmet le résultat à d'autres neurones par l'intermédiaire de l'axone. Dans notre modèle informatique, nous reproduisons ce processus avec :

• Entrées: Les signaux qui entrent dans le neurone (comme les dendrites qui reçoivent des signaux).
• Poids: L'importance attribuée à chaque entrée (analogue à la force des connexions synaptiques).
• Biais: Un paramètre supplémentaire qui aide le neurone à s'activer ou à rester inactif indépendamment des entrées.
• Fonction d'activation: Détermine si et avec quelle intensité le neurone "se déclenche" en fonction de ses entrées (de la même manière que le corps cellulaire décide de générer un potentiel d'action).
• Sortie: Le signal envoyé à la couche suivante (comme l'axone qui transmet à d'autres neurones).

Pour concrétiser cette idée, visualisons un seul neurone :

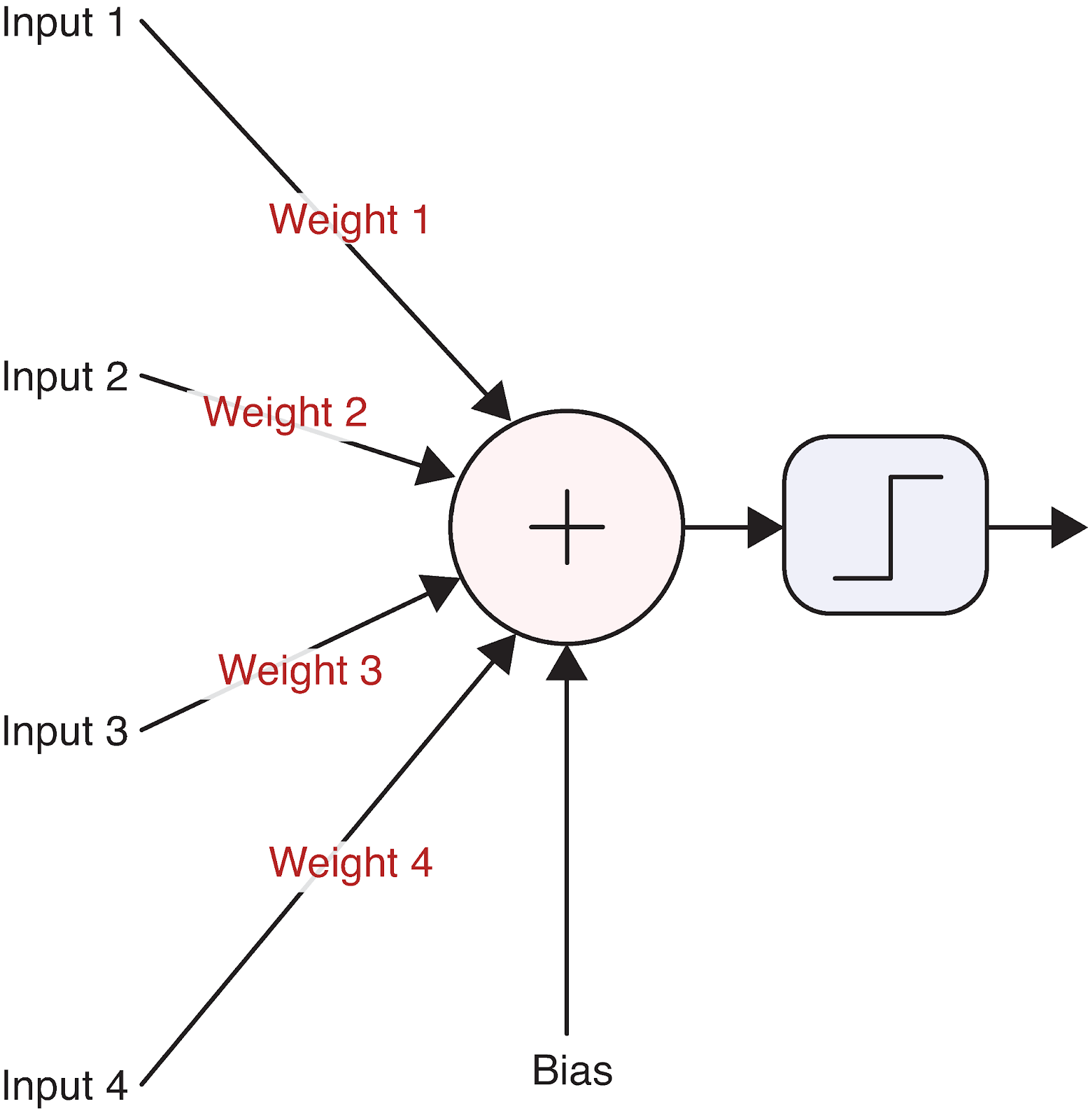
Source : Apprentissage profond - Approche visuelle

Cette simple unité de calcul est à la base des réseaux neuronaux les plus complexes. Mais comment un neurone transforme-t-il exactement ses entrées en sorties ? C'est là que les mathématiques entrent en jeu.

Fondement mathématique d'un neurone unique

Le fonctionnement d'un neurone peut être décrit par une équation simple :

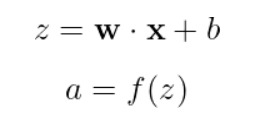
En résumé :

• x est notre vecteur d'entrée [x_1, x_2, x_3, ...]
• w est notre vecteur de poids [w_1, w_2, ..., w_n]
• b est le biais (une seule valeur scalaire)
• z est la somme pondérée plus le biais (souvent appelé "pré-activation" ou "logit")
• f est la fonction d'activation
• a est la sortie finale du neurone

Prenons un exemple concret avec des nombres réels. Supposons que nous ayons un neurone avec trois entrées :

Inputs: x = [2, 5, -1]
Weights: w = [0.5, -1, 2]
Bias: b = 0.5

Tout d'abord, nous calculons la somme pondérée plus le biais :

Ensuite, nous appliquons une fonction d'activation. Utilisons la fonction ReLU (Rectified Linear Unit), qui est définie comme suit :

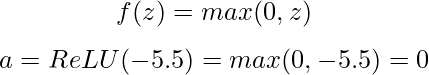
Avec une valeur de pré-activation négative, notre neurone ReLU émet 0, ce qui signifie qu'il ne se déclenche pas pour cette entrée particulière.

La fonction d'activation est cruciale car elle introduit la non-linéarité dans le réseau. Sans elle, les réseaux neuronaux seraient limités à l'apprentissage de relations linéaires, quel que soit le nombre de couches qu'ils comportent. Les fonctions d'activation les plus courantes sont les suivantes :

• Sigmoïde : 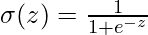Les sorties sont comprises entre 0 et 1, utile pour la classification binaire.
• ReLU : 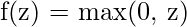Simple, efficace, et aide à résoudre le problème du gradient qui s'évanouit.
• Tanh : 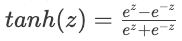- Sorties entre -1 et 1, souvent utilisées dans les couches cachées.

Chaque fonction d'activation a ses points forts et ses cas d'utilisation, que nous étudierons plus en détail lors de la mise en œuvre de notre réseau neuronal.

Des neurones aux couches

Les neurones individuels sont puissants, mais la véritable force des réseaux neuronaux apparaît lorsque les neurones sont organisés en couches. Une couche est simplement une collection de neurones qui traitent les entrées en parallèle. Un réseau neuronal comporte généralement trois types de couches :

1. Couche d'entrée : Reçoit les données brutes et les transmet à la couche suivante.
2. Couches cachées : Traiter les informations des couches précédentes
3. Couche de sortie : produit la prédiction ou la classification finale

Lorsque nous avons plusieurs neurones dans une couche, chacun recevant les mêmes entrées mais avec des poids et des biais différents, nous pouvons les représenter efficacement avec des opérations matricielles. Voyons comment cela fonctionne.

Imaginez que nous ayons une couche avec 3 valeurs d'entrée et 4 neurones. Chaque neurone a son propre ensemble de poids et de biais :

Inputs: x = [x₁, x₂, x₃]
Weights for neuron 1: w₁ = [w₁₁, w₁₂, w₁₃]
Weights for neuron 2: w₂ = [w₂₁, w₂₂, w₂₃]
Weights for neuron 3: w₃ = [w₃₁, w₃₂, w₃₃]
Weights for neuron 4: w₄ = [w₄₁, w₄₂, w₄₃]
Biases: b = [b₁, b₂, b₃, b₄]

Nous pouvons organiser ces poids dans une matrice W :

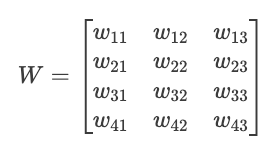
Nous pouvons maintenant calculer toutes les pré-activations des neurones en une seule fois, en multipliant la matrice :

Où ?

• X est notre vecteur d'entrée [x₁, x₂, x₃].
• W^T est la transposée de notre matrice de poids
• B est notre vecteur de biais [b₁, b₂, b₃, b₄].
• Z est le vecteur résultant des préactivations [z₁, z₂, z₃, z₄].

Nous appliquons ensuite la fonction d'activation par élément pour obtenir nos sorties finales :

Cette représentation matricielle n'est pas seulement une question d'élégance mathématique, c'est aussi une question d'efficacité informatique. Le matériel moderne (en particulier les GPU) est optimisé pour les opérations matricielles, ce qui rend cette approche beaucoup plus rapide que le calcul individuel de la sortie de chaque neurone.

La capacité à empiler ces couches - la sortie d'une couche devenant l'entrée de la suivante - est ce qui confère aux réseaux neuronaux leur remarquable capacité à apprendre des modèles complexes. En reliant ces éléments de base, nous sommes prêts à explorer le fonctionnement de la propagation vers l'avant dans l'ensemble d'un réseau neuronal.

Propagation vers l'avant à travers un réseau complet

Maintenant que nous comprenons les neurones et les couches individuels, prenons du recul et voyons comment la propagation vers l'avant fonctionne dans l'ensemble d'un réseau neuronal. C'est là qu'apparaît la véritable puissance de l'apprentissage profond.

Réseaux multicouches : le tableau complet

Un réseau neuronal complet se compose d'une couche d'entrée, d'une ou plusieurs couches cachées et d'une couche de sortie. Le terme "profond" dans l'apprentissage profond fait référence à des réseaux avec plusieurs couches cachées. Chaque couche transforme les données de manière de plus en plus abstraite, ce qui permet au réseau d'apprendre des représentations complexes.

Considérons un réseau neuronal simple avec :

• Une couche d'entrée avec 4 caractéristiques
• Deux couches cachées avec respectivement 3 et 2 neurones
• Une couche de sortie avec 3 neurones (peut-être pour une classification multi-classes)

Visuellement, ce réseau se présente comme suit :

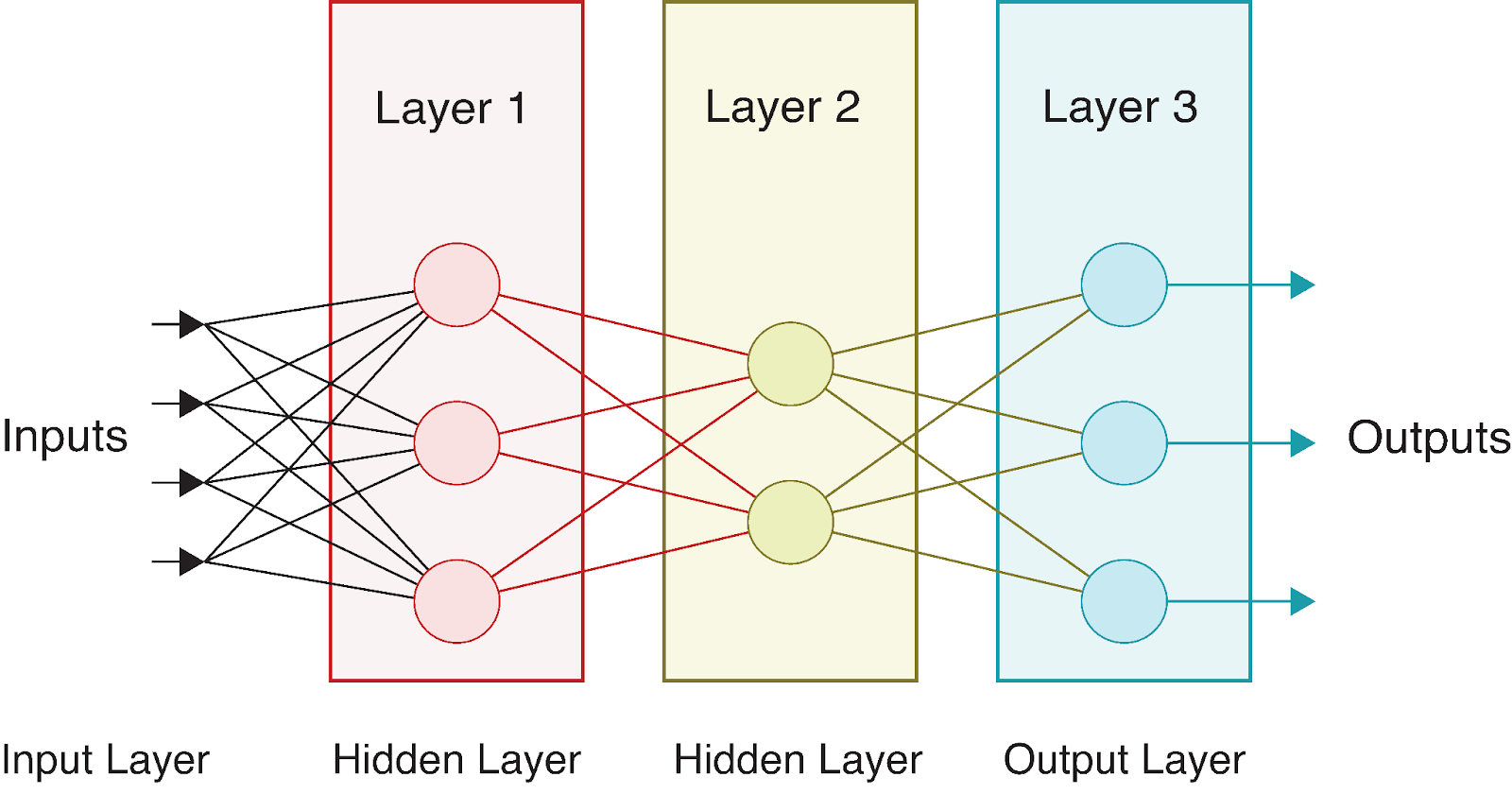
Au fur et à mesure que les données circulent dans ce réseau, nous effectuons une série de calculs à chaque couche. Si l'on dénote :

• Le vecteur d'entrée est X = [x_1, x_2, x_3, x_4].
• Matrices de poids : 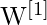(pour la couche cachée) et 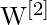(pour la couche de sortie).
• Les vecteurs de biais son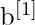t et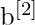
• Les fonctions d'activation sont f1 (pour la couche cachée) et f2 (pour la couche de sortie).

Nous pouvons exprimer la propagation vers l'avant à travers l'ensemble du réseau comme suit :

1. Calculez les pré-activations de la couche cachée : 

2. Appliquez la fonction d'activation pour obtenir les sorties de la couche cachée : 

3. Calculez les pré-activations de la couche de sortie : 

4. Appliquez la fonction d'activation pour obtenir les sorties finales :

La sortie finale A^[2] représente la prédiction du réseau. Pour les problèmes de classification, il peut s'agir des probabilités pour chaque classe ; pour la régression, il peut s'agir des valeurs prédites.

Les différentes couches utilisent souvent des fonctions d'activation différentes. Par exemple, les couches cachées utilisent généralement ReLU, tandis que les couches de sortie peuvent utiliser :

• Sigmoïde pour la classification binaire
• Softmax pour la classification multi-classes
• Linéaire (pas d'activation) pour la régression

L'intérêt de cette structure multicouche est que chaque couche peut apprendre à représenter différents aspects des données. Les premières couches détectent généralement des caractéristiques simples, tandis que les couches plus profondes les combinent pour former des modèles plus complexes. C'est cet apprentissage hiérarchique qui rend les réseaux neuronaux si puissants pour des tâches complexes telles que la reconnaissance d'images et de la parole.

Algorithme de propagation vers l'avant

Formalisons le processus de propagation vers l'avant sous la forme d'un algorithme. Pour un réseau neuronal à L couches, la propagation vers l'avant suit les étapes suivantes :

# Pseudocode for forward propagation
def forward_propagation(X, parameters):
   """
   X: Input data (batch_size, n_features)
   parameters: Dictionary containing weights and biases for each layer
   Returns: The final output and all intermediate activations
   """
   # Store all activations for later use (e.g., in backpropagation)
   activations = {'A0': X}  # A0 is the input
  
   # Loop through L-1 layers (excluding the output layer)
   for l in range(1, L):
       # Get previous activation
       A_prev = activations[f'A{l-1}']
      
       # Get weights and biases for current layer
       W = parameters[f'W{l}']
       b = parameters[f'b{l}']
      
       # Compute pre-activation
       Z = np.dot(A_prev, W.T) + b
      
       # Apply activation function (e.g., ReLU for hidden layers)
       A = relu(Z)
      
       # Store values for later use
       activations[f'Z{l}'] = Z
       activations[f'A{l}'] = A
  
   # Compute output layer (layer L)
   A_prev = activations[f'A{L-1}']
   W = parameters[f'W{L}']
   b = parameters[f'b{L}']
  
   # Compute pre-activation for output layer
   Z = np.dot(A_prev, W.T) + b
  
   # Apply output activation function (depends on the task)
   if task == 'binary_classification':
       A = sigmoid(Z)
   elif task == 'multiclass_classification':
       A = softmax(Z)
   elif task == 'regression':
       A = Z  # Linear activation
  
   # Store output layer values
   activations[f'Z{L}'] = Z
   activations[f'A{L}'] = A
  
   return A, activations

Cet algorithme met en évidence plusieurs aspects importants de la propagation vers l'avant :

1. Traitement séquentiel : L'information circule strictement vers l'avant, couche par couche.
2. Stockage d'activation : Nous stockons non seulement la sortie finale, mais aussi toutes les activations intermédiaires, qui seront cruciales pour l'entraînement du réseau à l'aide de la rétropropagation.
3. Sortie spécifique à la tâche : La fonction d'activation de la couche de sortie est choisie en fonction du problème spécifique (classification ou régression).

L'algorithme de propagation vers l'avant est remarquablement simple, mais il permet aux réseaux neuronaux d'approximer des fonctions incroyablement complexes. Combiné à un entraînement adéquat par rétropropagation, ce processus simple permet au réseau d'apprendre à partir des données et de faire des prédictions de plus en plus précises.

Prenons un exemple concret pour mieux comprendre. Considérons l'entrée X = [0,5, -0,2, 0,1] qui passe par notre réseau d'exemple avec :

• Poids de la couche cachée W^[1] (matrice 4×3) et biais b^[1] (vecteur de 4 valeurs)
• Pondérations de la couche de sortie W^[2] (matrice 2×4) et biais b^[2] (vecteur de 2 valeurs)

Pour simplifier, disons que toutes les pondérations sont de 0,1 et que tous les biais sont de 0 :

X = [0.5, -0.2, 0.1]
W[1] = [[0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1]]
b[1] = [0, 0, 0, 0]
W[2] = [[0.1, 0.1, 0.1, 0.1], [0.1, 0.1, 0.1, 0.1]]
b[2] = [0, 0]

En suivant notre algorithme :

• Première étape :

• Deuxième étape avec ReLU : 

• Troisième étape :

• Quatrième étape avec l'utilisation de la sigmoïde : 

Nous obtenons ainsi notre prédiction finale. Dans un contexte de classification binaire, ces valeurs proches de 0,5 indiqueraient une incertitude entre les deux classes.

Dans la section suivante, nous mettrons en œuvre la propagation vers l'avant en Python pour voir ces calculs en action.

Implémentation de la propagation vers l'avant en Python

Maintenant que nous comprenons la théorie derrière la propagation vers l'avant, mettons-la en pratique en l'implémentant en Python. Nous commencerons par une implémentation "à partir de zéro" en utilisant uniquement NumPy, puis nous verrons comment les cadres d'apprentissage profond modernes simplifient ce processus.

Construire à partir de zéro avec NumPy

NumPy fournit des opérations efficaces sur les tableaux qui nous permettent d'implémenter les calculs matriciels dont nous avons parlé. Construisons une classe de réseau neuronal simple qui effectue une propagation vers l'avant à travers plusieurs couches.

Tout d'abord, nous devons importer les bibliothèques nécessaires :

import numpy as np
import matplotlib.pyplot as plt

# For reproducibility
np.random.seed(42)

Définissons maintenant les fonctions d'activation que nous utiliserons dans notre réseau :

def relu(Z):
   """ReLU activation function: max(0, Z)"""
   return np.maximum(0, Z)

def sigmoid(Z):
   """Sigmoid activation function: 1/(1 + e^(-Z))"""
   return 1 / (1 + np.exp(-Z))

def softmax(Z):
   """Softmax activation function for multi-class classification"""
   # Subtract max for numerical stability (prevents overflow)
   exp_Z = np.exp(Z - np.max(Z, axis=1, keepdims=True))
   return exp_Z / np.sum(exp_Z, axis=1, keepdims=True)

Ensuite, créons une classe pour notre réseau neuronal :

class NeuralNetwork:
   def __init__(self, layer_dims, activations):
       """
       Initialize a neural network with specified layer dimensions and activations
      
       Parameters:
       - layer_dims: List of integers representing the number of neurons in each layer
                    (including input and output layers)
       - activations: List of activation functions for each layer (excluding input layer)
       """
       self.L = len(layer_dims) - 1  # Number of layers (excluding input layer)
       self.layer_dims = layer_dims
       self.activations = activations
       self.parameters = {}
      
       # Initialize parameters (weights and biases)
       self.initialize_parameters()
  
   def initialize_parameters(self):
       """Initialize weights and biases with small random values"""
       for l in range(1, self.L + 1):
           # He initialization for weights - helps with training deep networks
           self.parameters[f'W{l}'] = np.random.randn(self.layer_dims[l], self.layer_dims[l-1]) * np.sqrt(2 / self.layer_dims[l-1])
           self.parameters[f'b{l}'] = np.zeros((self.layer_dims[l], 1))
  
   def forward_propagation(self, X):
       """
       Perform forward propagation through the network
      
       Parameters:
       - X: Input data (n_features, batch_size)
      
       Returns:
       - AL: Output of the network
       - caches: Dictionary containing all activations and pre-activations
       """
       caches = {}
       A = X  # Input layer activation
       caches['A0'] = X
      
       # Process through L-1 layers (excluding output layer)
       for l in range(1, self.L):
           A_prev = A
          
           # Get weights and biases for current layer
           W = self.parameters[f'W{l}']
           b = self.parameters[f'b{l}']
          
           # Forward propagation for current layer
           Z = np.dot(W, A_prev) + b
          
           # Apply activation function
           activation_function = self.activations[l-1]
           if activation_function == "relu":
               A = relu(Z)
           elif activation_function == "sigmoid":
               A = sigmoid(Z)
          
           # Store values for backpropagation
           caches[f'Z{l}'] = Z
           caches[f'A{l}'] = A
      
       # Output layer
       W = self.parameters[f'W{self.L}']
       b = self.parameters[f'b{self.L}']
       Z = np.dot(W, A) + b
      
       # Apply output activation function
       activation_function = self.activations[self.L-1]
       if activation_function == "sigmoid":
           AL = sigmoid(Z)
       elif activation_function == "softmax":
           AL = softmax(Z)
       elif activation_function == "linear":
           AL = Z  # No activation for regression
      
       # Store output layer values
       caches[f'Z{self.L}'] = Z
       caches[f'A{self.L}'] = AL
      
       return AL, caches

La classe NeuralNetwork que nous avons mise en œuvre ci-dessus fournit un cadre complet pour la création et l'utilisation d'un réseau neuronal à l'architecture personnalisable. Décortiquons ses principaux éléments :

1. Initialisation: Le réseau est configuré avec des dimensions de couches et des fonctions d'activation spécifiques. Il initialise automatiquement les poids et les biais à l'aide de la méthode d'initialisation He pour une meilleure performance d'apprentissage.
2. Propagation vers l'avant: La méthode forward_propagation que nous venons de mettre en œuvre est au cœur de la capacité de prédiction du réseau neuronal. Il :

• Prend les données d'entrée et les fait passer par chaque couche
• Applique la fonction d'activation appropriée à chaque couche
• Stocke les valeurs intermédiaires dans des caches pour les utiliser ultérieurement dans la rétropropagation.
• renvoie à la fois la sortie finale et toutes les valeurs mises en cache

3. Fonctions d'activation: Le réseau prend en charge plusieurs fonctions d'activation, notamment ReLU, sigmoïde et softmax, ce qui lui permet de traiter différents types de problèmes (régression ou classification).

4. Architecture flexible: La mise en œuvre permet de créer des réseaux d'une profondeur et d'une largeur arbitraires, ce qui la rend adaptée à un large éventail de tâches d'apprentissage automatique.

Cette implémentation suit le modèle de conception standard des réseaux neuronaux, où les données circulent dans le réseau, chaque couche transformant les données avant de les transmettre à la couche suivante.

Testons maintenant notre implémentation avec un petit réseau d'exemple :

# Create a sample network
# Input layer: 3 features
# Hidden layer 1: 4 neurons with ReLU activation
# Output layer: 2 neurons with sigmoid activation (binary classification)
layer_dims = [3, 4, 2]
activations = ["relu", "sigmoid"]
nn = NeuralNetwork(layer_dims, activations)

# Create sample input data - 3 features for 5 examples
X = np.random.randn(3, 5)

# Perform forward propagation
output, caches = nn.forward_propagation(X)

print(f"Input shape: {X.shape}")
print(f"Output shape: {output.shape}")
print(f"Output values:\n{output}")

Sortie:

Input shape: (3, 5)
Output shape: (2, 5)
Output values:
[[0.00386784 0.54343014 0.39661893 0.5        0.51056934]
[0.11877049 0.32541093 0.44840699 0.5        0.45586633]]

Visualisons également comment les données se transforment au fur et à mesure qu'elles circulent dans le réseau :

def visualize_activations(caches, example_idx=0):
   """Visualize the activations for a single example through the network"""
   plt.figure(figsize=(15, 6))
  
   # Plot input
   plt.subplot(1, 3, 1)
   plt.bar(range(caches['A0'].shape[0]), caches['A0'][:, example_idx])
   plt.title('Input Layer')
   plt.xlabel('Feature')
   plt.ylabel('Value')
  
   # Plot hidden layer activation
   plt.subplot(1, 3, 2)
   plt.bar(range(caches['A1'].shape[0]), caches['A1'][:, example_idx])
   plt.title('Hidden Layer (ReLU Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   # Plot output layer
   plt.subplot(1, 3, 3)
   plt.bar(range(caches['A2'].shape[0]), caches['A2'][:, example_idx])
   plt.title('Output Layer (Sigmoid Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   plt.tight_layout()
   plt.show()

# Visualize the first example
visualize_activations(caches)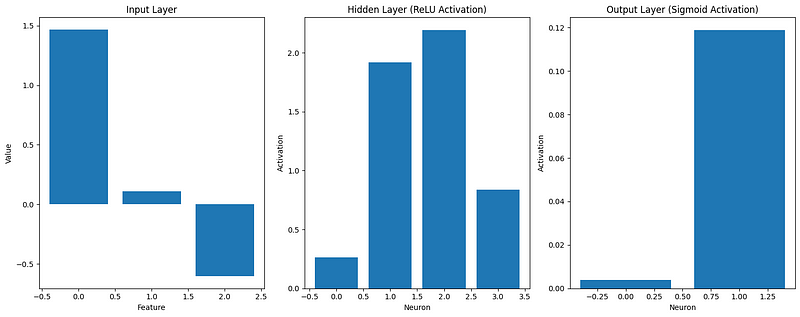

Cette visualisation nous aide à comprendre comment les données d'entrée sont transformées au fur et à mesure qu'elles se propagent dans le réseau. Nous pouvons le constater :

1. Les caractéristiques d'entrée peuvent avoir des valeurs positives ou négatives
2. Après l'activation ReLU dans la couche cachée, toutes les activations sont non négatives.
3. L'activation sigmoïde dans la couche de sortie contraint les valeurs entre 0 et 1.

Notre mise en œuvre "à partir de zéro" démontre les principes fondamentaux de la propagation vers l'avant, mais les cadres d'apprentissage profond modernes fournissent des outils plus efficaces et plus flexibles pour la construction de réseaux neuronaux.

Utiliser des cadres d'apprentissage profond

Mettons maintenant en œuvre le même réseau neuronal à l'aide des frameworks d'apprentissage profond les plus répandus : TensorFlow et PyTorch. Ces cadres optimisent les performances et fournissent des abstractions de plus haut niveau, ce qui facilite l'élaboration de modèles complexes.

Tout d'abord, examinons l'implémentation de TensorFlow/Keras :

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Input

# For reproducibility
tf.random.set_seed(42)

# Create the same network architecture
tf_model = Sequential([
   Input(shape=(3,)),  # Input layer with 3 features
   Dense(4, activation='relu'),  # Hidden layer with 4 neurons
   Dense(2, activation='sigmoid')  # Output layer with 2 neurons
])

tf_model.summary()

# Sample input data with the shape expected by Keras
X_tf = np.random.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in TensorFlow
tf_output = tf_model.predict(X_tf)

print(f"TensorFlow output shape: {tf_output.shape}")
print(f"TensorFlow output values:\n{tf_output}")

TensorFlow output shape: (5, 2)
TensorFlow output values:
[[0.6855308  0.7139542 ]
[0.4952355  0.5231934 ]
[0.50174904 0.5198488 ]
[0.44331825 0.6860926 ]
[0.6624589  0.5385444 ]]

Nous venons d'implémenter notre réseau neuronal à l'aide de TensorFlow/Keras et avons effectué avec succès une propagation vers l'avant sur quelques échantillons de données. Le résumé du modèle montre notre architecture avec une couche d'entrée acceptant 3 caractéristiques, une couche cachée avec 4 neurones utilisant l'activation ReLU, et une couche de sortie avec 2 neurones utilisant l'activation sigmoïde. Au total, le modèle comporte 26 paramètres entraînables.

Les résultats de la propagation vers l'avant montrent la forme de sortie (5, 2) correspondant à nos 5 exemples d'entrée, chacun produisant 2 valeurs de sortie. Ces sorties sont contraintes entre 0 et 1 en raison de la fonction d'activation sigmoïde dans la couche de sortie.

Ensuite, voyons comment nous pouvons mettre en œuvre la même architecture de réseau neuronal à l'aide de PyTorch, un autre cadre d'apprentissage profond populaire, afin de comparer les approches.

import torch
import torch.nn as nn

# For reproducibility
torch.manual_seed(42)

# Create a network in PyTorch
class PyTorchNN(nn.Module):
   def __init__(self):
       super(PyTorchNN, self).__init__()
       self.hidden = nn.Linear(3, 4)  # 3 inputs, 4 hidden neurons
       self.relu = nn.ReLU()
       self.output = nn.Linear(4, 2)  # 4 inputs from hidden, 2 outputs
       self.sigmoid = nn.Sigmoid()
  
   def forward(self, x):
       x = self.relu(self.hidden(x))
       x = self.sigmoid(self.output(x))
       return x

# Instantiate the model
torch_model = PyTorchNN()

# Print model structure
print(torch_model)

Sortie:

PyTorchNN(
 (hidden): Linear(in_features=3, out_features=4, bias=True)
 (relu): ReLU()
 (output): Linear(in_features=4, out_features=2, bias=True)
 (sigmoid): Sigmoid()
)

```python
# Sample input data
X_torch = torch.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in PyTorch
torch_output = torch_model(X_torch)

print(f"PyTorch output shape: {torch_output.shape}")
print(f"PyTorch output values:\n{torch_output}")

Sortie:

PyTorch output shape: torch.Size([5, 2])
PyTorch output values:
tensor([[0.4516, 0.4116],
       [0.4289, 0.4267],
       [0.4278, 0.4172],
       [0.3771, 0.4321],
       [0.5769, 0.3328]], grad_fn=<SigmoidBackward0>)

Comparons nos implémentations :

# Compare dimensions and structure of outputs
print("\nComparison of implementations:")
print(f"NumPy output shape: {output.shape}")
print(f"TensorFlow output shape: {tf_output.shape}")
print(f"PyTorch output shape: {torch_output.shape}")

Sortie:

Comparison of implementations:
NumPy output shape: (2, 5)
TensorFlow output shape: (5, 2)
PyTorch output shape: torch.Size([5, 2])

Les principales différences entre nos implémentations :

1. Structure et lisibilité:

• NumPy : La mise en œuvre explicite de chaque étape permet un contrôle et une transparence complets.
• TensorFlow/Keras : Les abstractions de haut niveau cachent les détails de la mise en œuvre mais simplifient le code.
• PyTorch : Approche orientée objet avec méthode explicite

2. Performance:

• TensorFlow et PyTorch optimisent les opérations pour l'accélération GPU
• Les deux cadres mettent en œuvre un calcul efficace du gradient pour l'entraînement
• Les frameworks optimisent l'utilisation de la mémoire pour les grands réseaux

3. Extensibilité:

• Les frameworks fournissent des composants pré-construits (couches, optimiseurs, etc.).
• Outils intégrés pour l'enregistrement/le chargement de modèles, la visualisation et le déploiement
• Soutien et documentation étendus de la part de la communauté

Pour les réseaux simples, notre implémentation NumPy fonctionne bien, mais au fur et à mesure que la complexité augmente, les cadres d'apprentissage profond deviennent essentiels. Ils gèrent les optimisations de bas niveau et fournissent des outils pour l'ensemble du flux de travail de l'apprentissage automatique, du développement au déploiement. Pour en savoir plus sur ces cadres, consultez nos guides distincts :

• Tutoriel PyTorch : Construire un réseau neuronal simple à partir de zéro
• Tutoriel TensorFlow pour les débutants 

Dans la section suivante, nous construirons un exemple complet qui applique la propagation vers l'avant à un problème réel.

Exemple de propagation vers l'avant

Maintenant que nous avons mis en œuvre la propagation vers l'avant à la fois à partir de zéro et en utilisant des frameworks populaires, voyons-la en action sur un problème réel. Nous construirons un exemple complet et étudierons comment optimiser le processus pour de meilleures performances.

Exemple complet de fonctionnement

Appliquons notre compréhension à un problème classique d'apprentissage automatique : la reconnaissance de chiffres manuscrits à l'aide de l'ensemble de données MNIST. Cet ensemble de données contient 70 000 images de chiffres manuscrits (0-9), chacune d'une taille de 28x28 pixels.

Commençons par charger et préparer les données :

from tensorflow.keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt

# Load MNIST dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# Normalize pixel values to range [0, 1]
X_train = X_train / 255.0
X_test = X_test / 255.0

# Reshape images to vectors (flatten 28x28 to 784)
X_train_flat = X_train.reshape(X_train.shape[0], -1).T  # Shape: (784, 60000)
X_test_flat = X_test.reshape(X_test.shape[0], -1).T     # Shape: (784, 10000)

# Convert labels to one-hot encoding
def one_hot_encode(y, num_classes=10):
   one_hot = np.zeros((num_classes, y.size))
   one_hot[y, np.arange(y.size)] = 1
   return one_hot

y_train_one_hot = one_hot_encode(y_train)  # Shape: (10, 60000)
y_test_one_hot = one_hot_encode(y_test)    # Shape: (10, 10000)

# Display sample images
plt.figure(figsize=(10, 5))
for i in range(5):
   plt.subplot(1, 5, i+1)
   plt.imshow(X_train[i], cmap='gray')
   plt.title(f"Label: {y_train[i]}")
   plt.axis('off')
plt.tight_layout()
plt.show()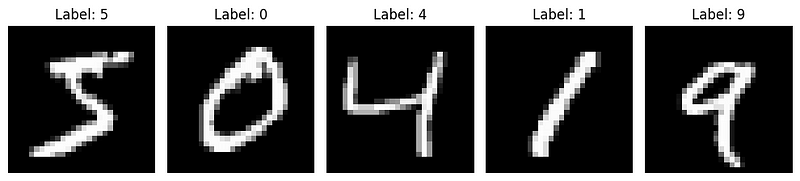

Construisons maintenant un réseau neuronal pour cette tâche à l'aide de notre implémentation NumPy. Nous créerons un réseau avec :

• Couche d'entrée: 784 neurones (28x28 pixels)
• Couche cachée: 128 neurones avec activation ReLU
• Couche de sortie: 10 neurones avec activation softmax (pour 10 chiffres)

# Define our network architecture
layer_dims = [784, 128, 10]
activations = ["relu", "softmax"]
nn = NeuralNetwork(layer_dims, activations)

# Take a small batch for demonstration
batch_size = 64
batch_indices = np.random.choice(X_train_flat.shape[1], batch_size, replace=False)
X_batch = X_train_flat[:, batch_indices]
y_batch = y_train_one_hot[:, batch_indices]

# Perform forward propagation
output, caches = nn.forward_propagation(X_batch)

# Compute accuracy
predictions = np.argmax(output, axis=0)
true_labels = np.argmax(y_batch, axis=0)
accuracy = np.mean(predictions == true_labels)

print(f"Batch accuracy: {accuracy:.4f}")

Out: Batch accuracy: 0.0781

Nous avons obtenu une précision de 7 %, ce qui est pire qu'un modèle de devinettes aléatoires. Mais c'est normal puisque nous n'effectuons qu'une propagation vers l'avant - il n'y a pas d'apprentissage.

Visualisons maintenant comment le réseau traite une seule image à travers chaque couche :

def visualize_network_processing(nn, image, label, caches):
   """Visualize network processing for a single image"""
   plt.figure(figsize=(15, 10))
  
   # Plot original image
   plt.subplot(2, 3, 1)
   plt.imshow(image.reshape(28, 28), cmap='gray')
   plt.title(f"Input Image (Digit: {label})")
   plt.axis('off')
  
   # Plot flattened input (first 100 values)
   plt.subplot(2, 3, 2)
   plt.bar(range(100), image.flatten()[:100])
   plt.title("Input Layer (first 100 pixels)")
   plt.xlabel("Pixel Index")
   plt.ylabel("Pixel Value")
  
   # Plot hidden layer activations (first 50 neurons)
   plt.subplot(2, 3, 3)
   hidden_activations = caches['A1'][:50, 0]
   plt.bar(range(len(hidden_activations)), hidden_activations)
   plt.title("Hidden Layer Activations (first 50 neurons)")
   plt.xlabel("Neuron Index")
   plt.ylabel("Activation")
  
   # Plot output layer activations
   plt.subplot(2, 3, 4)
   output_activations = caches['A2'][:, 0]
   plt.bar(range(10), output_activations)
   plt.xticks(range(10))
   plt.title("Output Layer Activations (Softmax)")
   plt.xlabel("Digit Class")
   plt.ylabel("Probability")
  
   # Plot prediction vs actual
   plt.subplot(2, 3, 5)
   prediction = np.argmax(output_activations)
   plt.bar(['Actual', 'Predicted'], [label, prediction], color=['blue', 'orange'])
   plt.title(f"Prediction: {prediction}, Actual: {label}")
   plt.ylabel("Digit")
  
   plt.tight_layout()
   plt.show()

# Visualize forward propagation for the first image in our batch
image_idx = 0
image = X_batch[:, image_idx].reshape(784, 1)
label = true_labels[image_idx]

visualize_network_processing(nn, image, label, caches)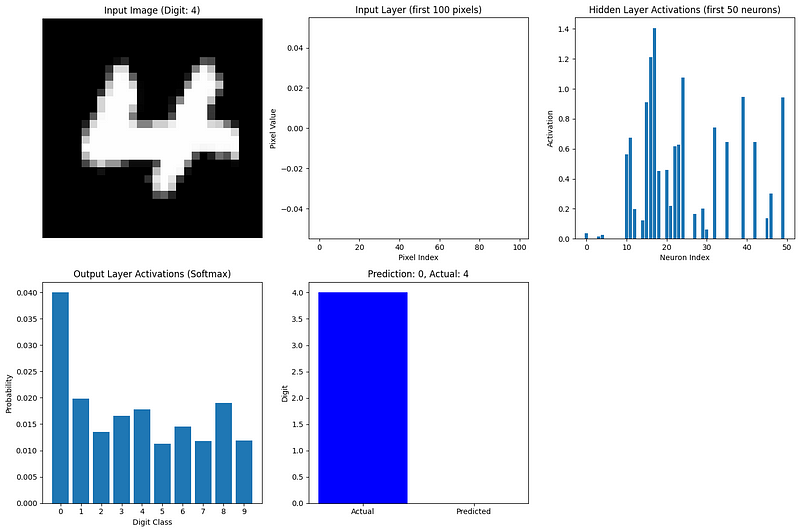

Cette visualisation montre comment l'information circule dans notre réseau :

1. Couche d'entrée: Les pixels de l'image aplatie (valeurs entre 0 et 1)
2. Couche cachée: Les neurones activés par ReLU captent différentes caractéristiques du chiffre
3. Couche de sortie: L'activation softmax donne une distribution de probabilité sur les 10 chiffres possibles

Le neurone de sortie le plus actif correspond à la prédiction du réseau. Même avec des poids aléatoires (puisque nous n'avons pas encore entraîné le réseau), nous pouvons voir comment la propagation vers l'avant transforme les données d'entrée en une prédiction.

Pour un exemple plus complet, nous formerions ce réseau en utilisant la rétropropagation pour ajuster les poids et les biais, améliorant ainsi les prédictions au fil du temps. Cependant, même sans formation, cet exemple démontre le processus de propagation vers l'avant sur des données réelles.

Optimisation de la propagation vers l'avant

À mesure que les réseaux neuronaux prennent de l'ampleur et que les ensembles de données deviennent plus volumineux, l'optimisation de la propagation vers l'avant devient cruciale. Voici quelques stratégies clés pour améliorer l'efficacité de la propagation vers l'avant :

1. Traitement par lots

Plutôt que de traiter un exemple à la fois, nous calculons la propagation vers l'avant sur des lots d'exemples simultanément. Cela permet d'exploiter les capacités de traitement parallèle du matériel moderne.

2. Vectorisation

L'utilisation d'opérations matricielles au lieu de boucles accélère considérablement les calculs. C'est pourquoi notre implémentation a utilisé les opérations de tableau de NumPy.

3. Gestion de la mémoire

Pour les grands réseaux, nous devons faire attention à l'utilisation de la mémoire. Les techniques comprennent :

• Réutilisation de la mémoire pour les activations intermédiaires.
• Calculer les activations couche par couche sans stocker tous les intermédiaires.
• L'utilisation de représentations de moindre précision (par exemple, des nombres flottants de 16 bits au lieu de 32 bits).

4. Accélération par le GPU

Les unités de traitement graphique excellent dans les opérations matricielles. Les cadres modernes peuvent déplacer de manière transparente les calculs vers les GPU, ce qui permet d'obtenir des accélérations significatives :

# TensorFlow example of GPU acceleration
import tensorflow as tf

# Check for available GPUs
print("GPUs Available:", tf.config.list_physical_devices('GPU'))

# TensorFlow automatically uses available GPUs
with tf.device('/GPU:0'):  # Explicitly specify GPU if multiple are available
   # Computation runs on GPU if available
   result = tf_model.predict(X_tf)

5. Matériel spécialisé

Outre les GPU, des équipements tels que les Tensor Processing Units (TPU) de Google sont spécifiquement conçus pour les opérations de réseaux neuronaux.

6. Optimisations algorithmiques

Certaines fonctions d'activation et architectures de réseau sont conçues pour être efficaces en termes de calcul :

• ReLU est plus rapide à calculer que sigmoïde ou tanh.
• Les convolutions séparables en profondeur réduisent les calculs par rapport aux convolutions standard.
• L'élagage du réseau supprime les connexions inutiles, ce qui réduit les calculs.

7. Optimisation du cadre de travail

Les cadres d'apprentissage profond mettent en œuvre de nombreuses optimisations de bas niveau :

• Les opérations fusionnées combinent plusieurs étapes dans des noyaux optimisés uniques.
• Des algorithmes auto-adaptatifs sélectionnent l'implémentation la plus rapide pour un matériel spécifique.
• La compilation JIT (Just-In-Time) crée un code optimisé pour des configurations réseau spécifiques.

À mesure que les réseaux deviennent plus profonds et plus larges, l'optimisation de la propagation vers l'avant devient de plus en plus importante. Les architectures modernes telles que les ResNets, les Transformers et les EfficientNets intègrent des choix de conception visant spécifiquement à rendre la propagation vers l'avant plus efficace tout en maintenant ou en améliorant la précision du modèle.

Dans la section suivante, nous verrons comment la propagation vers l'avant se connecte à la propagation vers l'arrière (rétropropagation), complétant ainsi le tableau de la manière dont les réseaux neuronaux apprennent.

La relation avec la rétropropagation

Nous avons maintenant exploré en profondeur la propagation vers l'avant, mais ce n'est que la moitié de l'histoire lorsqu'il s'agit de réseaux neuronaux. Examinons brièvement le lien entre la propagation vers l'avant et la rétropropagation, l'algorithme qui permet aux réseaux neuronaux d'apprendre.

Connecter la propagation vers l'avant et vers l'arrière

La propagation vers l'avant et la rétropropagation sont des processus complémentaires dans les réseaux neuronaux :

• Propagation vers l'avant prend des données d'entrée et produit des prédictions, en se déplaçant de gauche à droite dans le réseau.
• La rétropropagation prend en compte les erreurs et produit des mises à jour de poids, en se déplaçant de droite à gauche dans le réseau.

Ces deux processus sont indissociables dans le processus d'apprentissage. La rétropropagation ne peut avoir lieu sans que la propagation vers l'avant ne soit d'abord effectuée, comme elle doit l'être :

1. Les activations de chaque couche (que nous avons stockées dans nos caches).
2. La prédiction finale à comparer à l'étiquette réelle.
3. L'architecture du réseau et les poids utilisés lors de la propagation vers l'avant.

Considérez la propagation vers l'avant comme un réseau neuronal qui fait sa meilleure estimation, compte tenu de sa compréhension actuelle, tandis que la rétropropagation lui permet d'affiner cette compréhension sur la base de ses erreurs.

La boucle d'apprentissage

L'ensemble du processus d'apprentissage suit un schéma cyclique :

1. Propagation vers l'avant: Le réseau traite les données d'entrée et fait des prédictions.
2. Calcul des pertes: Les prévisions sont comparées aux cibles réelles pour calculer l'erreur.
3. Propagation à rebours: L'erreur est propagée vers l'arrière dans le réseau afin de déterminer la contribution de chaque poids à l'erreur.
4. Mise à jour du poids: Les poids sont ajustés pour réduire l'erreur.
5. Répétez: Le processus se poursuit avec de nouvelles données jusqu'à ce que le réseau fonctionne bien.

La puissance de ce processus réside dans le fait que la propagation vers l'avant fournit le contexte nécessaire à la rétropropagation. Lors de la propagation vers l'avant, le réseau ne se contente pas de faire des prédictions, mais garde également une trace de toutes les valeurs et décisions intermédiaires. La rétropropagation utilise ensuite ces informations pour procéder à des ajustements ciblés.

La beauté de ce système réside dans le fait qu'un apprentissage complexe émerge de ces deux processus relativement simples qui fonctionnent ensemble. La propagation vers l'avant est simple - il s'agit simplement de multiplications de matrices et de fonctions d'activation appliquées de manière séquentielle. La rétropropagation est plus complexe, mais elle découle directement des principes du calcul.

Ensemble, ils permettent aux réseaux neuronaux d'apprendre pratiquement n'importe quel modèle s'ils disposent de suffisamment de données et de ressources informatiques. Cette capacité d'apprentissage a permis des percées dans les domaines de la vision artificielle, du traitement du langage naturel, des jeux et d'innombrables autres domaines.

La compréhension approfondie de la propagation vers l'avant, comme nous l'avons fait dans cet article, fournit les bases nécessaires pour appréhender l'ensemble du processus d'apprentissage dans les réseaux neuronaux. Si vous souhaitez approfondir l'aspect apprentissage, notre guide sur la rétropropagation explique en détail comment les réseaux apprennent de leurs erreurs.

Conclusion et prochaines étapes

La propagation vers l'avant est le processus fondamental qui permet aux réseaux neuronaux de transformer les données d'entrée en prévisions. Comme nous l'avons vu, il s'agit de multiplications séquentielles de matrices et de fonctions d'activation qui transforment progressivement les données à travers les couches du réseau. Il est essentiel de comprendre ce processus, que vous mettiez en place des réseaux à partir de zéro, que vous utilisiez des cadres modernes ou que vous dépanniez les performances d'un modèle. 

En maîtrisant la propagation vers l'avant, vous avez fait un grand pas vers la construction et la compréhension de modèles d'apprentissage profond capables de résoudre des problèmes complexes dans tous les domaines.

Pour poursuivre votre voyage d'apprentissage en profondeur, explorez les ressources complètes de DataCamp : 

• Plongez dans les mathématiques qui sous-tendent les réseaux neuronaux avec Introduction aux réseaux neuronaux profonds
• Maîtrisez le processus de formation avec Maîtriser la rétropropagation
• Obtenez une expérience pratique de la construction de réseaux avec PyTorch ou R.

Pour un parcours d'apprentissage structuré, le programme Apprentissage profond en Python cursus fournit tout ce dont vous avez besoin pour devenir compétent dans la construction et le déploiement de réseaux neuronaux pour des applications du monde réel.