Propagação direta em redes neurais: Um guia completo

As redes neurais revolucionaram a inteligência artificial, potencializando tudo, desde o reconhecimento de imagens até o processamento de linguagem natural. No centro desses modelos avançados está um processo fundamental chamado de propagação direta. Este guia explorará esse conceito central, levando você dos princípios básicos à implementação prática. 

Se você estiver procurando um guia prático para muitos dos conceitos que abordamos aqui, não deixe de conferir nossa Programa de habilidades de aprendizagem profunda em Python.

O que é propagação direta?

A propagação direta é o processo pelo qual uma rede neural transforma dados de entrada em previsões ou saídas. Pense nisso como a fase de "pensamento" de uma rede neural - quando é mostrada uma entrada (como uma imagem ou texto), a propagação direta é como a rede processa essas informações por meio de suas camadas para produzir um resultado.

Em termos técnicos, é o cálculo sequencial que move os dados da camada de entrada, através das camadas ocultas e, finalmente, para a camada de saída. Durante essa jornada, os dados são transformados por conexões ponderadas e funções de ativação, permitindo que a rede capture padrões complexos.

Por que é importante entender a propagação direta

Entender a propagação direta é fundamental por vários motivos:

1. Base para o aprendizado: Você não pode entender como as redes neurais aprendem sem antes entender como elas fazem previsões. A propagação direta é o pré-requisito para você compreender a retropropagaçãoo algoritmo que permite o aprendizado.
2. Depuração e otimização: Quando as redes neurais não apresentam um bom desempenho, saber como os dados fluem pela rede ajuda você a identificar e corrigir problemas.
3. Projeto do modelo: Um projeto de arquitetura eficaz requer a compreensão de como as informações se propagam por meio de diferentes configurações de camadas.
4. Eficiência de implantação: A otimização da propagação direta é essencial para a implementação de modelos em ambientes com recursos limitados.

O que você aprenderá neste guia

Ao final deste guia abrangente, você terá:

• Compreender a matemática por trás dos cálculos de redes neurais
• Ser capaz de implementar a propagação direta do zero usando o NumPy
• Você sabe como usar estruturas modernas, como TensorFlow e PyTorch, para uma propagação eficiente
• Visualize como as informações se transformam à medida que passam por uma rede
• Conectar a propagação direta ao processo de aprendizado mais amplo em redes neurais
• Implementar um exemplo de trabalho completo em dados reais

Pré-requisitos

Para aproveitar ao máximo este guia, você deve ter:

• Conhecimento básico de programação Python
• Familiaridade com conceitos matemáticos fundamentais (vetores, matrizes e cálculo básico)
• Você tem alguma exposição a conceitos de machine learning

Se você precisa fortalecer sua base, considere estes recursos:

• Introdução às redes neurais profundas para os principais conceitos.
• Introdução à aprendizagem profunda em Python para que você tenha uma experiência de aprendizado interativa.
• Criando uma rede neural simples a partir do zero para que você possa praticar.

Mesmo sem um amplo conhecimento prévio, elaboramos este guia para desenvolver conceitos de forma progressiva, tornando as redes neurais acessíveis a alunos determinados. Vamos mergulhar de cabeça!

Fundamentos da propagação direta

Para entender a propagação direta, precisamos começar com seus blocos de construção fundamentais. Vamos começar com a menor unidade de computação em redes neurais e, gradualmente, aumentar para estruturas mais complexas.

O neurônio único: onde tudo começa

A jornada da rede neural começa com um paralelo fascinante com a biologia. Assim como o cérebro humano é composto por bilhões de neurônios interconectados, as redes neurais artificiais são construídas a partir de modelos matemáticos inspirados nessas células biológicas.

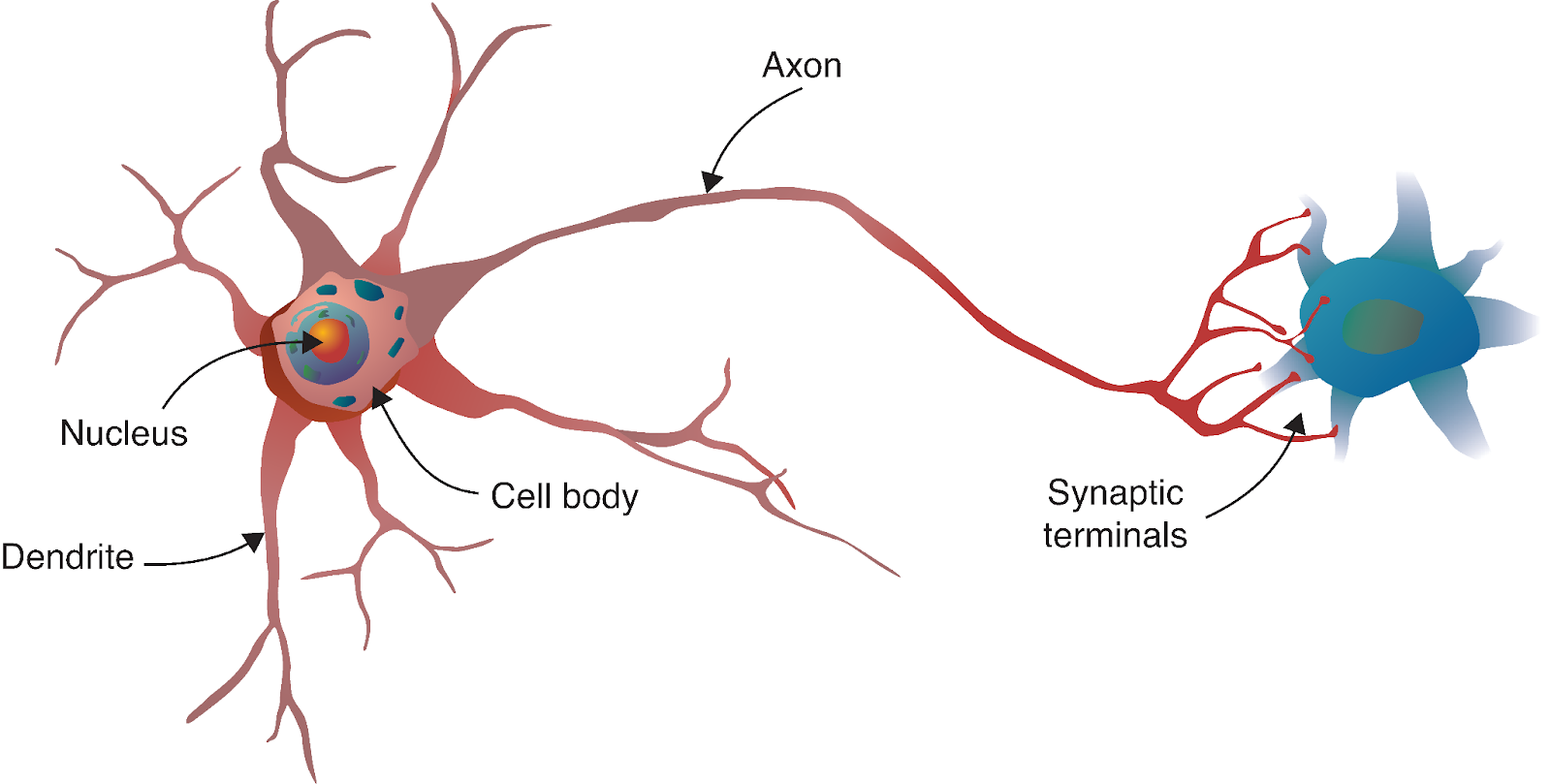
Fonte: Aprendizagem profunda - abordagem visual

Um neurônio biológico recebe sinais de outros neurônios por meio de dendritos, processa esses sinais em seu corpo celular e, em seguida, transmite o resultado por meio do axônio para outros neurônios. Em nosso modelo computacional, espelhamos esse processo com:

• Entradas: Os sinais que chegam ao neurônio (como os dendritos que recebem sinais).
• Pesos: A importância atribuída a cada entrada (análoga à força das conexões sinápticas).
• Viés: Um parâmetro adicional que ajuda o neurônio a se ativar ou permanecer inativo, independentemente das entradas.
• Função de ativação: Determina se e com que intensidade o neurônio "dispara" com base em suas entradas (semelhante ao corpo celular que decide se vai gerar um potencial de ação).
• Saída: O sinal enviado para a próxima camada (como o axônio que transmite para outros neurônios).

Vamos visualizar um único neurônio para tornar isso concreto:

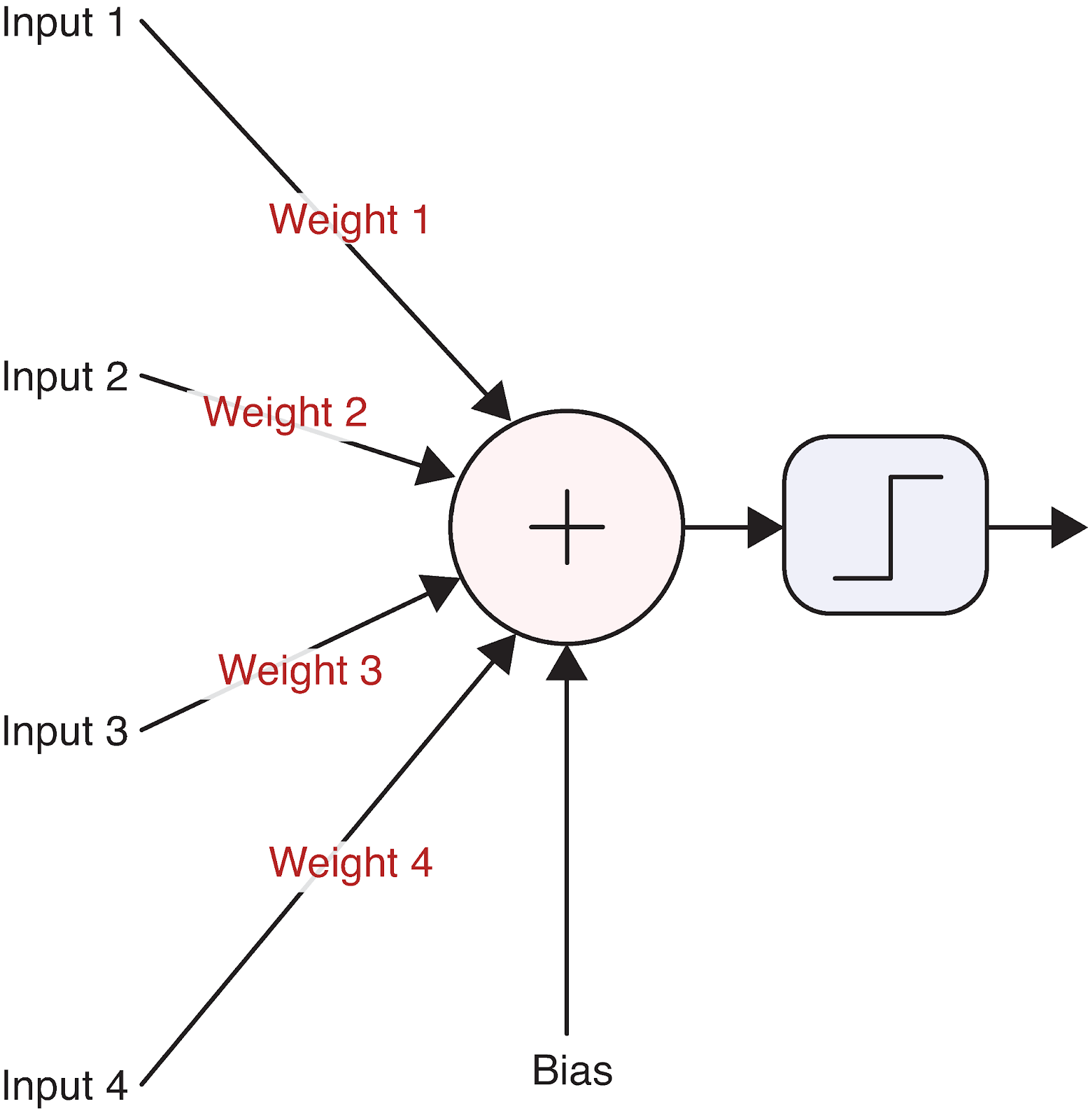
Fonte: Aprendizagem profunda - abordagem visual

Essa unidade computacional simples forma a base até mesmo das redes neurais mais complexas. Mas como exatamente um neurônio transforma suas entradas em uma saída? É aqui que entra a matemática.

Base matemática de um único neurônio

A operação de um neurônio pode ser descrita com uma equação simples:

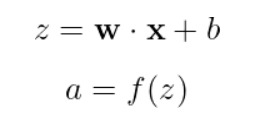
Desmembrando isso:

• x é o nosso vetor de entrada [x_1, x_2, x_3, ...]
• w é o nosso vetor de peso [w_1, w_2, ..., w_n]
• b é a polarização (um único valor escalar)
• z é a soma ponderada mais o viés (geralmente chamado de "pré-ativação" ou "logit")
• f é a função de ativação
• a é a saída final do neurônio

Vamos analisar um exemplo concreto com números reais. Digamos que temos um neurônio com três entradas:

Inputs: x = [2, 5, -1]
Weights: w = [0.5, -1, 2]
Bias: b = 0.5

Primeiro, calculamos a soma ponderada mais o viés:

Em seguida, aplicamos uma função de ativação. Vamos usar a popular função ReLU (Rectified Linear Unit), que é definida como:

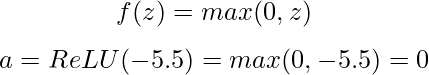
Com um valor de pré-ativação negativo, nosso neurônio ReLU produz 0, o que significa que ele não "dispara" para essa entrada específica.

A função de ativação é fundamental porque introduz a não linearidade na rede. Sem ele, as redes neurais estariam limitadas a aprender apenas relações lineares, independentemente do número de camadas que tivessem. As funções de ativação comuns incluem:

• Sigmoide: 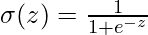saídas entre 0 e 1, útil para classificação binária
• ReLU: 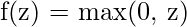Simples, eficiente e ajuda com o problema do gradiente de fuga
• Tanh: 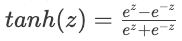de Tanh - Produz resultados entre -1 e 1, geralmente usados em camadas ocultas

Cada função de ativação tem seus pontos fortes e casos de uso, que exploraremos mais quando implementarmos nossa rede neural.

De neurônios a camadas

Os neurônios individuais são poderosos, mas a verdadeira força das redes neurais surge quando os neurônios são organizados em camadas. Uma camada é simplesmente um conjunto de neurônios que processam entradas em paralelo. Normalmente, há três tipos de camadas em uma rede neural:

1. Camada de entrada: Recebe os dados brutos e os passa para a próxima camada
2. Camadas ocultas: Processar informações das camadas anteriores
3. Camada de saída: Produz a previsão ou classificação final

Quando temos vários neurônios em uma camada, cada um recebendo as mesmas entradas, mas com diferentes pesos e polarizações, podemos representar isso de forma eficiente com operações de matriz. Vamos ver como isso funciona.

Imagine que temos uma camada com 3 valores de entrada e 4 neurônios. Cada neurônio tem seu próprio conjunto de pesos e polarização:

Inputs: x = [x₁, x₂, x₃]
Weights for neuron 1: w₁ = [w₁₁, w₁₂, w₁₃]
Weights for neuron 2: w₂ = [w₂₁, w₂₂, w₂₃]
Weights for neuron 3: w₃ = [w₃₁, w₃₂, w₃₃]
Weights for neuron 4: w₄ = [w₄₁, w₄₂, w₄₃]
Biases: b = [b₁, b₂, b₃, b₄]

Podemos organizar esses pesos em uma matriz W:

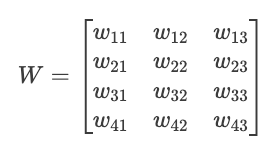
Agora podemos computar todas as pré-ativações dos neurônios de uma só vez com uma única multiplicação de matriz:

Onde:

• X é nosso vetor de entrada [x₁, x₂, x₃]
• W^T é a transposição de nossa matriz de pesos
• B é o nosso vetor de viés [b₁, b₂, b₃, b₄]
• Z é o vetor resultante de pré-ativações [z₁, z₂, z₃, z₄]

Em seguida, aplicamos a função de ativação em todos os elementos para obter nossos resultados finais:

Essa representação matricial não é apenas elegância matemática; é também eficiência computacional. O hardware moderno (especialmente as GPUs) é otimizado para operações de matriz, o que torna essa abordagem muito mais rápida do que calcular a saída de cada neurônio individualmente.

A capacidade de empilhar essas camadas - com a saída de uma camada tornando-se a entrada da próxima - é o que dá às redes neurais sua notável capacidade de aprender padrões complexos. Quando conectamos esses blocos de construção, estamos prontos para explorar como a propagação direta funciona em uma rede neural inteira.

Propagação direta por meio de uma rede completa

Agora que entendemos os neurônios e as camadas individuais, vamos dar um passo atrás e ver como a propagação direta funciona em uma rede neural inteira. É aqui que surge o verdadeiro poder da aprendizagem profunda.

Redes multicamadas: o quadro completo

Uma rede neural completa consiste em uma camada de entrada, uma ou mais camadas ocultas e uma camada de saída. O termo "profundo" na aprendizagem profunda refere-se a redes com várias camadas ocultas. Cada camada transforma os dados de forma cada vez mais abstrata, permitindo que a rede aprenda representações complexas.

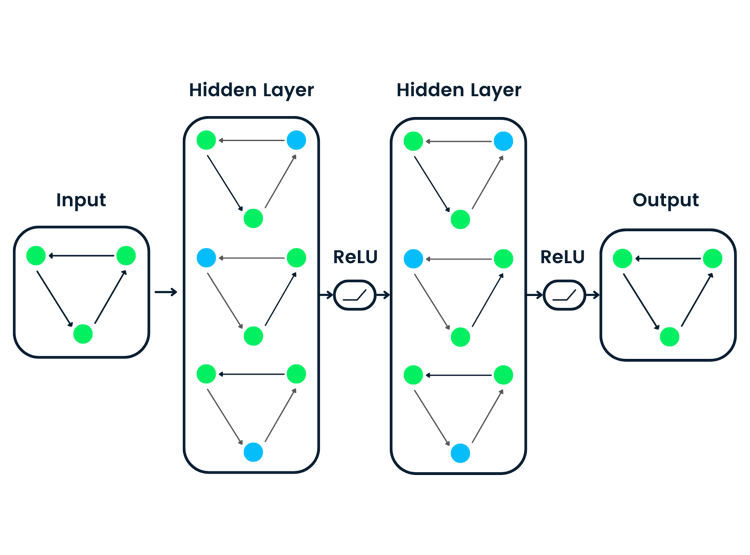
Vamos considerar uma rede neural simples com:

• Uma camada de entrada com 4 recursos
• Duas camadas ocultas com 3 e 2 neurônios, respectivamente
• Uma camada de saída com 3 neurônios (talvez para classificação de várias classes)

Visualmente, essa rede tem a seguinte aparência:

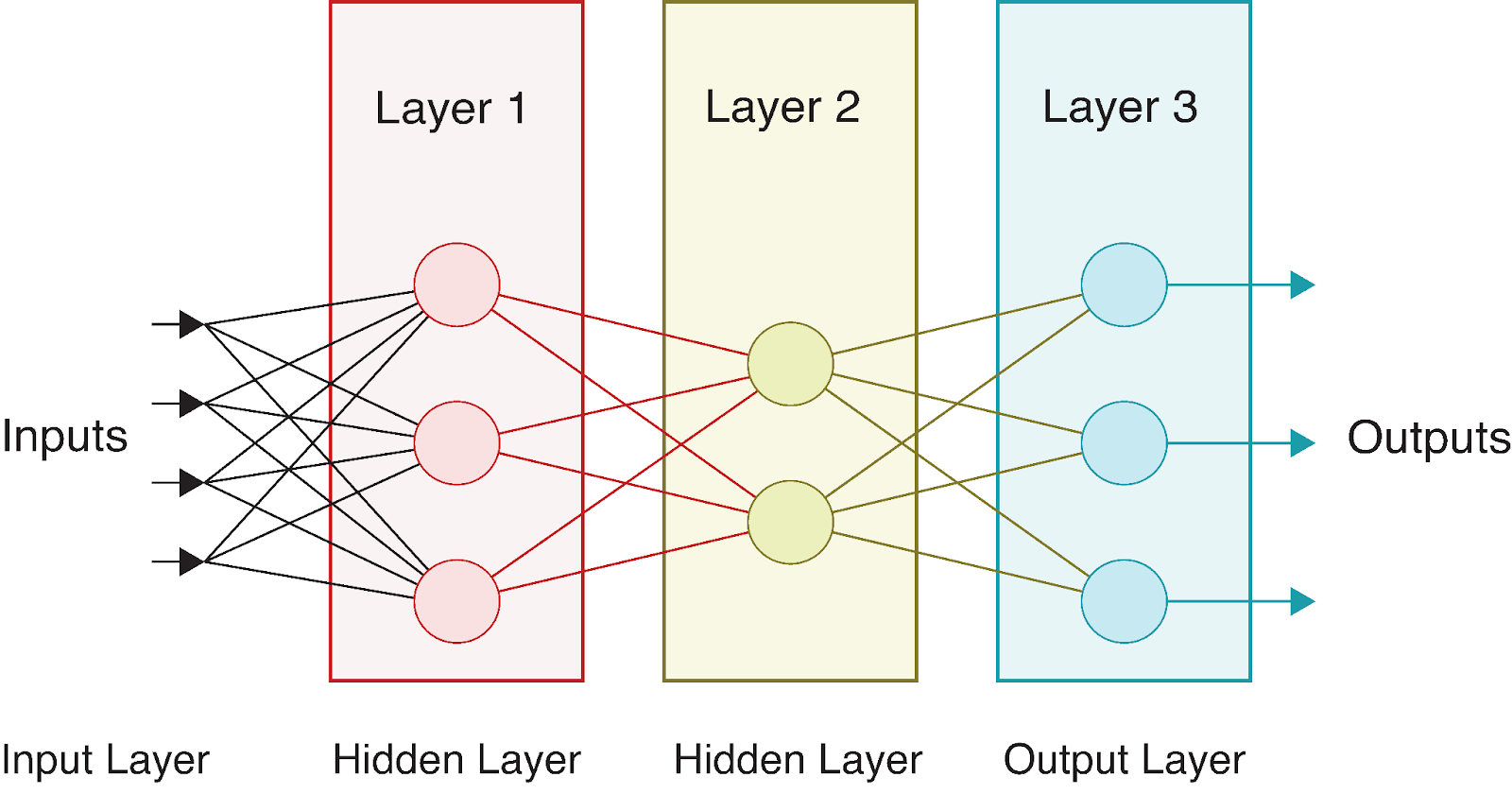
À medida que os dados fluem por essa rede, realizamos uma série de cálculos em cada camada. Se denotarmos:

• Vetor de entrada como X = [x_1, x_2, x_3, x_4]
• Matrizes de peso como 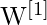(para a camada oculta) e 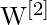(para a camada de saída)
• Vetores de viés como 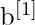e
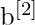
• Funções de ativação como f1 (para a camada oculta) e f2 (para a camada de saída)

Podemos expressar a propagação direta por toda essa rede como:

1. Calcule as pré-ativações da camada oculta: 

2. Aplique a função de ativação para obter as saídas da camada oculta: 

3. Calcule as pré-ativações da camada de saída: 

4. Aplique a função de ativação para obter os outputs finais:

O resultado final A^[2] representa a previsão da rede. Para problemas de classificação, podem ser as probabilidades de cada classe; para regressão, podem ser os valores previstos.

Camadas diferentes geralmente usam funções de ativação diferentes. Por exemplo, as camadas ocultas normalmente usam ReLU, enquanto as camadas de saída podem usar:

• Sigmoide para classificação binária
• Softmax para classificação multiclasse
• Linear (sem ativação) para regressão

A vantagem dessa estrutura de várias camadas é que cada camada pode aprender a representar diferentes aspectos dos dados. As camadas iniciais normalmente detectam recursos simples, enquanto as camadas mais profundas os combinam em padrões mais complexos. Esse aprendizado hierárquico é o que torna as redes neurais tão poderosas para tarefas complexas, como reconhecimento de imagem e fala.

Algoritmo de propagação direta

Vamos formalizar o processo de propagação para frente em um algoritmo. Para uma rede neural com L camadas, a propagação direta segue estas etapas:

# Pseudocode for forward propagation
def forward_propagation(X, parameters):
   """
   X: Input data (batch_size, n_features)
   parameters: Dictionary containing weights and biases for each layer
   Returns: The final output and all intermediate activations
   """
   # Store all activations for later use (e.g., in backpropagation)
   activations = {'A0': X}  # A0 is the input
  
   # Loop through L-1 layers (excluding the output layer)
   for l in range(1, L):
       # Get previous activation
       A_prev = activations[f'A{l-1}']
      
       # Get weights and biases for current layer
       W = parameters[f'W{l}']
       b = parameters[f'b{l}']
      
       # Compute pre-activation
       Z = np.dot(A_prev, W.T) + b
      
       # Apply activation function (e.g., ReLU for hidden layers)
       A = relu(Z)
      
       # Store values for later use
       activations[f'Z{l}'] = Z
       activations[f'A{l}'] = A
  
   # Compute output layer (layer L)
   A_prev = activations[f'A{L-1}']
   W = parameters[f'W{L}']
   b = parameters[f'b{L}']
  
   # Compute pre-activation for output layer
   Z = np.dot(A_prev, W.T) + b
  
   # Apply output activation function (depends on the task)
   if task == 'binary_classification':
       A = sigmoid(Z)
   elif task == 'multiclass_classification':
       A = softmax(Z)
   elif task == 'regression':
       A = Z  # Linear activation
  
   # Store output layer values
   activations[f'Z{L}'] = Z
   activations[f'A{L}'] = A
  
   return A, activations

Esse algoritmo destaca vários aspectos importantes da propagação direta:

1. Processamento sequencial: As informações fluem estritamente para frente, camada por camada.
2. Armazenamento de ativação: Armazenamos não apenas a saída final, mas todas as ativações intermediárias, que serão cruciais para o treinamento da rede usando a retropropagação.
3. Saída específica da tarefa: A função de ativação para a camada de saída é escolhida com base no problema específico (classificação vs. regressão).

O algoritmo de propagação direta é extremamente simples, mas permite que as redes neurais aproximem funções incrivelmente complexas. Quando combinado com o treinamento adequado por meio da retropropagação, esse processo simples permite que a rede aprenda com os dados e faça previsões cada vez mais precisas.

Vamos analisar um exemplo específico para solidificar ainda mais nosso entendimento. Considere a entrada X = [0,5, -0,2, 0,1] passando pela nossa rede de exemplo com:

• Pesos da camada oculta W^[1] (matriz 4×3) e polarizações b^[1] (vetor de 4 valores)
• Pesos da camada de saída W^[2] (matriz 2×4) e polarizações b^[2] (vetor de 2 valores)

Para simplificar, digamos que todos os pesos sejam 0,1 e todas as tendências sejam 0:

X = [0.5, -0.2, 0.1]
W[1] = [[0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1], [0.1, 0.1, 0.1]]
b[1] = [0, 0, 0, 0]
W[2] = [[0.1, 0.1, 0.1, 0.1], [0.1, 0.1, 0.1, 0.1]]
b[2] = [0, 0]

Seguindo nosso algoritmo:

• Primeira etapa:

• Segunda etapa com o ReLU: 

• Terceira etapa:

• Quarta etapa com o uso do sigmoide: 

Isso nos dá nossa previsão final. Em um contexto de classificação binária, esses valores próximos a 0,5 indicariam incerteza entre as duas classes.

Na próxima seção, implementaremos a propagação direta em Python para que você veja esses cálculos em ação.

Implementando a propagação direta em Python

Agora que entendemos a teoria por trás da propagação para frente, vamos colocá-la em prática implementando-a em Python. Começaremos com uma implementação "do zero" usando apenas o NumPy e, em seguida, veremos como as estruturas modernas de aprendizagem profunda simplificam esse processo.

Construindo do zero com o NumPy

O NumPy oferece operações de matriz eficientes que nos permitem implementar os cálculos de matriz que discutimos. Vamos criar uma classe de rede neural simples que executa a propagação direta por meio de várias camadas.

Primeiro, precisamos importar as bibliotecas necessárias:

import numpy as np
import matplotlib.pyplot as plt

# For reproducibility
np.random.seed(42)

Agora, vamos definir as funções de ativação que usaremos em nossa rede:

def relu(Z):
   """ReLU activation function: max(0, Z)"""
   return np.maximum(0, Z)

def sigmoid(Z):
   """Sigmoid activation function: 1/(1 + e^(-Z))"""
   return 1 / (1 + np.exp(-Z))

def softmax(Z):
   """Softmax activation function for multi-class classification"""
   # Subtract max for numerical stability (prevents overflow)
   exp_Z = np.exp(Z - np.max(Z, axis=1, keepdims=True))
   return exp_Z / np.sum(exp_Z, axis=1, keepdims=True)

Em seguida, vamos criar uma classe para nossa rede neural:

class NeuralNetwork:
   def __init__(self, layer_dims, activations):
       """
       Initialize a neural network with specified layer dimensions and activations
      
       Parameters:
       - layer_dims: List of integers representing the number of neurons in each layer
                    (including input and output layers)
       - activations: List of activation functions for each layer (excluding input layer)
       """
       self.L = len(layer_dims) - 1  # Number of layers (excluding input layer)
       self.layer_dims = layer_dims
       self.activations = activations
       self.parameters = {}
      
       # Initialize parameters (weights and biases)
       self.initialize_parameters()
  
   def initialize_parameters(self):
       """Initialize weights and biases with small random values"""
       for l in range(1, self.L + 1):
           # He initialization for weights - helps with training deep networks
           self.parameters[f'W{l}'] = np.random.randn(self.layer_dims[l], self.layer_dims[l-1]) * np.sqrt(2 / self.layer_dims[l-1])
           self.parameters[f'b{l}'] = np.zeros((self.layer_dims[l], 1))
  
   def forward_propagation(self, X):
       """
       Perform forward propagation through the network
      
       Parameters:
       - X: Input data (n_features, batch_size)
      
       Returns:
       - AL: Output of the network
       - caches: Dictionary containing all activations and pre-activations
       """
       caches = {}
       A = X  # Input layer activation
       caches['A0'] = X
      
       # Process through L-1 layers (excluding output layer)
       for l in range(1, self.L):
           A_prev = A
          
           # Get weights and biases for current layer
           W = self.parameters[f'W{l}']
           b = self.parameters[f'b{l}']
          
           # Forward propagation for current layer
           Z = np.dot(W, A_prev) + b
          
           # Apply activation function
           activation_function = self.activations[l-1]
           if activation_function == "relu":
               A = relu(Z)
           elif activation_function == "sigmoid":
               A = sigmoid(Z)
          
           # Store values for backpropagation
           caches[f'Z{l}'] = Z
           caches[f'A{l}'] = A
      
       # Output layer
       W = self.parameters[f'W{self.L}']
       b = self.parameters[f'b{self.L}']
       Z = np.dot(W, A) + b
      
       # Apply output activation function
       activation_function = self.activations[self.L-1]
       if activation_function == "sigmoid":
           AL = sigmoid(Z)
       elif activation_function == "softmax":
           AL = softmax(Z)
       elif activation_function == "linear":
           AL = Z  # No activation for regression
      
       # Store output layer values
       caches[f'Z{self.L}'] = Z
       caches[f'A{self.L}'] = AL
      
       return AL, caches

A classe NeuralNetwork que implementamos acima fornece uma estrutura completa para criar e usar uma rede neural com arquitetura personalizável. Vamos detalhar seus principais componentes:

1. Inicialização: A rede é configurada com dimensões de camada e funções de ativação especificadas. Ele inicializa automaticamente os pesos e as tendências usando o método de inicialização He para melhorar o desempenho do treinamento.
2. Propagação direta: O método forward_propagation que acabamos de implementar é o coração da capacidade de previsão da rede neural. It:

• Recebe os dados de entrada e os passa por cada camada
• Aplica a função de ativação apropriada em cada camada
• Armazena valores intermediários em caches para uso posterior na retropropagação
• Retorna a saída final e todos os valores armazenados em cache

3. Funções de ativação: A rede suporta várias funções de ativação, incluindo ReLU, sigmoide e softmax, o que permite lidar com diferentes tipos de problemas (regressão ou classificação).

4. Arquitetura flexível: A implementação permite redes de profundidade e largura arbitrárias, o que a torna adequada para uma ampla gama de tarefas de machine learning.

Essa implementação segue o padrão de design de rede neural padrão, em que os dados fluem pela rede, com cada camada transformando os dados antes de passá-los para a próxima camada.

Agora vamos testar nossa implementação com um pequeno exemplo de rede:

# Create a sample network
# Input layer: 3 features
# Hidden layer 1: 4 neurons with ReLU activation
# Output layer: 2 neurons with sigmoid activation (binary classification)
layer_dims = [3, 4, 2]
activations = ["relu", "sigmoid"]
nn = NeuralNetwork(layer_dims, activations)

# Create sample input data - 3 features for 5 examples
X = np.random.randn(3, 5)

# Perform forward propagation
output, caches = nn.forward_propagation(X)

print(f"Input shape: {X.shape}")
print(f"Output shape: {output.shape}")
print(f"Output values:\n{output}")

Saída:

Input shape: (3, 5)
Output shape: (2, 5)
Output values:
[[0.00386784 0.54343014 0.39661893 0.5        0.51056934]
[0.11877049 0.32541093 0.44840699 0.5        0.45586633]]

Vamos também visualizar como os dados se transformam à medida que fluem pela rede:

def visualize_activations(caches, example_idx=0):
   """Visualize the activations for a single example through the network"""
   plt.figure(figsize=(15, 6))
  
   # Plot input
   plt.subplot(1, 3, 1)
   plt.bar(range(caches['A0'].shape[0]), caches['A0'][:, example_idx])
   plt.title('Input Layer')
   plt.xlabel('Feature')
   plt.ylabel('Value')
  
   # Plot hidden layer activation
   plt.subplot(1, 3, 2)
   plt.bar(range(caches['A1'].shape[0]), caches['A1'][:, example_idx])
   plt.title('Hidden Layer (ReLU Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   # Plot output layer
   plt.subplot(1, 3, 3)
   plt.bar(range(caches['A2'].shape[0]), caches['A2'][:, example_idx])
   plt.title('Output Layer (Sigmoid Activation)')
   plt.xlabel('Neuron')
   plt.ylabel('Activation')
  
   plt.tight_layout()
   plt.show()

# Visualize the first example
visualize_activations(caches)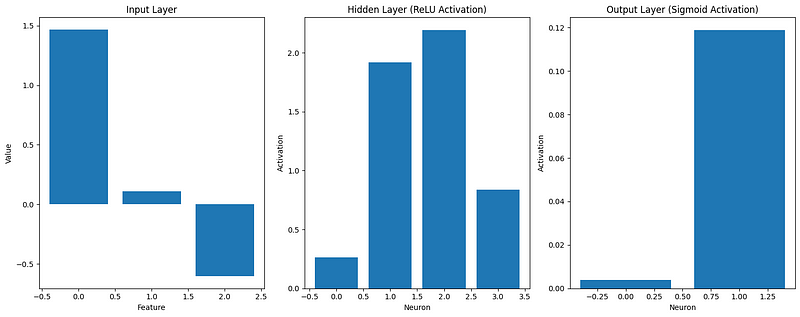

Essa visualização nos ajuda a entender como os dados de entrada são transformados à medida que se propagam pela rede. Podemos ver isso:

1. Os recursos de entrada podem ter valores positivos ou negativos
2. Após a ativação do ReLU na camada oculta, todas as ativações são não negativas
3. A ativação sigmoide na camada de saída restringe os valores entre 0 e 1

Nossa implementação "do zero" demonstra os princípios fundamentais da propagação direta, mas as estruturas modernas de aprendizagem profunda oferecem ferramentas mais eficientes e flexíveis para a criação de redes neurais.

Uso de estruturas de aprendizagem profunda

Agora, vamos implementar a mesma rede neural usando estruturas populares de aprendizagem profunda: TensorFlow e PyTorch. Essas estruturas otimizam o desempenho e fornecem abstrações de nível superior, facilitando a criação de modelos complexos.

Primeiro, vamos dar uma olhada na implementação do TensorFlow/Keras:

import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Input

# For reproducibility
tf.random.set_seed(42)

# Create the same network architecture
tf_model = Sequential([
   Input(shape=(3,)),  # Input layer with 3 features
   Dense(4, activation='relu'),  # Hidden layer with 4 neurons
   Dense(2, activation='sigmoid')  # Output layer with 2 neurons
])

tf_model.summary()

# Sample input data with the shape expected by Keras
X_tf = np.random.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in TensorFlow
tf_output = tf_model.predict(X_tf)

print(f"TensorFlow output shape: {tf_output.shape}")
print(f"TensorFlow output values:\n{tf_output}")

TensorFlow output shape: (5, 2)
TensorFlow output values:
[[0.6855308  0.7139542 ]
[0.4952355  0.5231934 ]
[0.50174904 0.5198488 ]
[0.44331825 0.6860926 ]
[0.6624589  0.5385444 ]]

Acabamos de implementar nossa rede neural usando o TensorFlow/Keras e realizamos com sucesso a propagação direta em alguns dados de amostra. O resumo do modelo mostra nossa arquitetura com uma camada de entrada que aceita 3 recursos, uma camada oculta com 4 neurônios usando ativação ReLU e uma camada de saída com 2 neurônios usando ativação sigmoide. No total, o modelo tem 26 parâmetros treináveis.

Os resultados da propagação direta mostram a forma de saída (5, 2) correspondente aos nossos 5 exemplos de entrada, cada um produzindo 2 valores de saída. Essas saídas são limitadas entre 0 e 1 devido à função de ativação sigmoide na camada de saída.

Em seguida, vamos ver como podemos implementar a mesma arquitetura de rede neural usando o PyTorch, outra estrutura popular de aprendizagem profunda, para comparar as abordagens.

import torch
import torch.nn as nn

# For reproducibility
torch.manual_seed(42)

# Create a network in PyTorch
class PyTorchNN(nn.Module):
   def __init__(self):
       super(PyTorchNN, self).__init__()
       self.hidden = nn.Linear(3, 4)  # 3 inputs, 4 hidden neurons
       self.relu = nn.ReLU()
       self.output = nn.Linear(4, 2)  # 4 inputs from hidden, 2 outputs
       self.sigmoid = nn.Sigmoid()
  
   def forward(self, x):
       x = self.relu(self.hidden(x))
       x = self.sigmoid(self.output(x))
       return x

# Instantiate the model
torch_model = PyTorchNN()

# Print model structure
print(torch_model)

Saída:

PyTorchNN(
 (hidden): Linear(in_features=3, out_features=4, bias=True)
 (relu): ReLU()
 (output): Linear(in_features=4, out_features=2, bias=True)
 (sigmoid): Sigmoid()
)

```python
# Sample input data
X_torch = torch.randn(5, 3)  # 5 examples, 3 features

# Forward propagation in PyTorch
torch_output = torch_model(X_torch)

print(f"PyTorch output shape: {torch_output.shape}")
print(f"PyTorch output values:\n{torch_output}")

Saída:

PyTorch output shape: torch.Size([5, 2])
PyTorch output values:
tensor([[0.4516, 0.4116],
       [0.4289, 0.4267],
       [0.4278, 0.4172],
       [0.3771, 0.4321],
       [0.5769, 0.3328]], grad_fn=<SigmoidBackward0>)

Vamos comparar nossas implementações:

# Compare dimensions and structure of outputs
print("\nComparison of implementations:")
print(f"NumPy output shape: {output.shape}")
print(f"TensorFlow output shape: {tf_output.shape}")
print(f"PyTorch output shape: {torch_output.shape}")

Saída:

Comparison of implementations:
NumPy output shape: (2, 5)
TensorFlow output shape: (5, 2)
PyTorch output shape: torch.Size([5, 2])

As principais diferenças entre nossas implementações:

1. Estrutura e legibilidade:

• NumPy: A implementação explícita de cada etapa proporciona total controle e transparência
• TensorFlow/Keras: As abstrações de alto nível ocultam os detalhes da implementação, mas tornam o código mais simples
• PyTorch: Abordagem orientada a objetos com método avançado explícito

2. Desempenho:

• O TensorFlow e o PyTorch otimizam as operações para aceleração de GPU
• Ambas as estruturas implementam a computação eficiente de gradiente para treinamento
• As estruturas otimizam o uso da memória para grandes redes

3. Extensibilidade:

• As estruturas fornecem componentes pré-construídos (camadas, otimizadores, etc.)
• Ferramentas integradas para salvar/carregar modelos, visualização e implementação
• Amplo suporte e documentação da comunidade

Para redes simples, nossa implementação do NumPy funciona bem, mas à medida que a complexidade aumenta, as estruturas de aprendizagem profunda se tornam essenciais. Eles lidam com otimizações de baixo nível e fornecem ferramentas para todo o fluxo de trabalho de machine learning, desde o desenvolvimento até a implantação. Para saber mais sobre essas estruturas, consulte nossos guias separados:

• PyTorch Tutorial: Criando uma rede neural simples a partir do zero
• Tutorial do TensorFlow para iniciantes 

Na próxima seção, criaremos um exemplo de trabalho completo que aplica a propagação progressiva a um problema do mundo real.

Exemplo de propagação direta

Agora que implementamos a propagação direta do zero e usando estruturas populares, vamos vê-la em ação em um problema do mundo real. Criaremos um exemplo completo e exploraremos como otimizar o processo para melhorar o desempenho.

Exemplo de trabalho completo

Vamos aplicar nosso entendimento a um problema clássico de machine learning: reconhecimento de dígitos manuscritos usando o conjunto de dados MNIST. Esse conjunto de dados contém 70.000 imagens de dígitos manuscritos (0-9), cada um com 28x28 pixels de tamanho.

Primeiro, vamos carregar e preparar os dados:

from tensorflow.keras.datasets import mnist
import numpy as np
import matplotlib.pyplot as plt

# Load MNIST dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()

# Normalize pixel values to range [0, 1]
X_train = X_train / 255.0
X_test = X_test / 255.0

# Reshape images to vectors (flatten 28x28 to 784)
X_train_flat = X_train.reshape(X_train.shape[0], -1).T  # Shape: (784, 60000)
X_test_flat = X_test.reshape(X_test.shape[0], -1).T     # Shape: (784, 10000)

# Convert labels to one-hot encoding
def one_hot_encode(y, num_classes=10):
   one_hot = np.zeros((num_classes, y.size))
   one_hot[y, np.arange(y.size)] = 1
   return one_hot

y_train_one_hot = one_hot_encode(y_train)  # Shape: (10, 60000)
y_test_one_hot = one_hot_encode(y_test)    # Shape: (10, 10000)

# Display sample images
plt.figure(figsize=(10, 5))
for i in range(5):
   plt.subplot(1, 5, i+1)
   plt.imshow(X_train[i], cmap='gray')
   plt.title(f"Label: {y_train[i]}")
   plt.axis('off')
plt.tight_layout()
plt.show()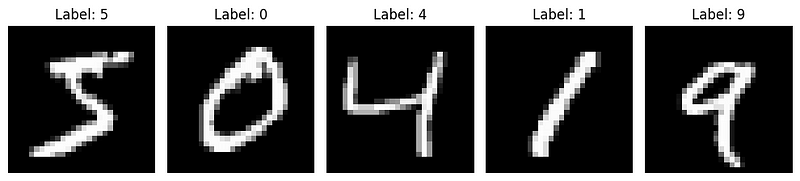

Agora, vamos criar uma rede neural para essa tarefa usando nossa implementação do NumPy. Criaremos uma rede com você:

• Camada de entrada: 784 neurônios (28x28 pixels)
• Camada oculta: 128 neurônios com ativação de ReLU
• Camada de saída: 10 neurônios com ativação softmax (para 10 dígitos)

# Define our network architecture
layer_dims = [784, 128, 10]
activations = ["relu", "softmax"]
nn = NeuralNetwork(layer_dims, activations)

# Take a small batch for demonstration
batch_size = 64
batch_indices = np.random.choice(X_train_flat.shape[1], batch_size, replace=False)
X_batch = X_train_flat[:, batch_indices]
y_batch = y_train_one_hot[:, batch_indices]

# Perform forward propagation
output, caches = nn.forward_propagation(X_batch)

# Compute accuracy
predictions = np.argmax(output, axis=0)
true_labels = np.argmax(y_batch, axis=0)
accuracy = np.mean(predictions == true_labels)

print(f"Batch accuracy: {accuracy:.4f}")

Out: Batch accuracy: 0.0781

Temos 7% de precisão, o que é pior até do que um modelo de adivinhação aleatória. Mas isso é esperado, pois estamos realizando apenas a propagação direta - não há aprendizado envolvido.

Agora, vamos visualizar como a rede processa uma única imagem em cada camada:

def visualize_network_processing(nn, image, label, caches):
   """Visualize network processing for a single image"""
   plt.figure(figsize=(15, 10))
  
   # Plot original image
   plt.subplot(2, 3, 1)
   plt.imshow(image.reshape(28, 28), cmap='gray')
   plt.title(f"Input Image (Digit: {label})")
   plt.axis('off')
  
   # Plot flattened input (first 100 values)
   plt.subplot(2, 3, 2)
   plt.bar(range(100), image.flatten()[:100])
   plt.title("Input Layer (first 100 pixels)")
   plt.xlabel("Pixel Index")
   plt.ylabel("Pixel Value")
  
   # Plot hidden layer activations (first 50 neurons)
   plt.subplot(2, 3, 3)
   hidden_activations = caches['A1'][:50, 0]
   plt.bar(range(len(hidden_activations)), hidden_activations)
   plt.title("Hidden Layer Activations (first 50 neurons)")
   plt.xlabel("Neuron Index")
   plt.ylabel("Activation")
  
   # Plot output layer activations
   plt.subplot(2, 3, 4)
   output_activations = caches['A2'][:, 0]
   plt.bar(range(10), output_activations)
   plt.xticks(range(10))
   plt.title("Output Layer Activations (Softmax)")
   plt.xlabel("Digit Class")
   plt.ylabel("Probability")
  
   # Plot prediction vs actual
   plt.subplot(2, 3, 5)
   prediction = np.argmax(output_activations)
   plt.bar(['Actual', 'Predicted'], [label, prediction], color=['blue', 'orange'])
   plt.title(f"Prediction: {prediction}, Actual: {label}")
   plt.ylabel("Digit")
  
   plt.tight_layout()
   plt.show()

# Visualize forward propagation for the first image in our batch
image_idx = 0
image = X_batch[:, image_idx].reshape(784, 1)
label = true_labels[image_idx]

visualize_network_processing(nn, image, label, caches)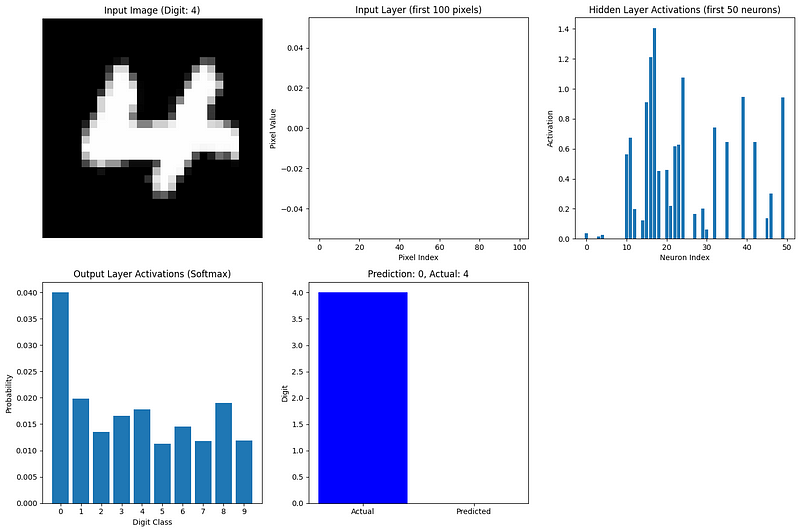

Esta visualização mostra como as informações fluem em nossa rede:

1. Camada de entrada: Os pixels achatados da imagem (valores entre 0 e 1)
2. Camada oculta: Os neurônios ativados pelo ReLU captam diferentes recursos do dígito
3. Camada de saída: A ativação do softmax fornece uma distribuição de probabilidade sobre os 10 dígitos possíveis

O neurônio de saída mais ativo corresponde à previsão da rede. Mesmo com pesos aleatórios (já que ainda não treinamos a rede), podemos ver como a propagação direta transforma os dados de entrada em uma previsão.

Para um exemplo mais completo, treinaríamos essa rede usando a retropropagação para ajustar os pesos e as tendências, melhorando as previsões ao longo do tempo. No entanto, mesmo sem treinamento, esse exemplo demonstra o processo de propagação progressiva em dados reais.

Otimização da propagação direta

À medida que as redes neurais aumentam e os conjuntos de dados se tornam mais volumosos, a otimização da propagação direta se torna crucial. Aqui estão as principais estratégias para tornar a propagação direta mais eficiente:

1. Processamento em lote

Em vez de processar um exemplo por vez, calculamos a propagação direta em lotes de exemplos simultaneamente. Isso aproveita os recursos de processamento paralelo do hardware moderno.

2. Vetorização

O uso de operações de matriz em vez de loops acelera drasticamente a computação. É por isso que nossa implementação usou as operações de matriz do NumPy.

3. Gerenciamento de memória

Em redes grandes, precisamos ter cuidado com o uso da memória. As técnicas incluem:

• Reutilização da memória para ativações intermediárias.
• Computação das ativações camada por camada sem armazenar todos os intermediários.
• Usar representações de menor precisão (por exemplo, floats de 16 bits em vez de 32 bits).

4. Aceleração de GPU

As unidades de processamento gráfico são excelentes em operações de matriz. As estruturas modernas podem mover perfeitamente a computação para GPUs para obter aumentos significativos de velocidade:

# TensorFlow example of GPU acceleration
import tensorflow as tf

# Check for available GPUs
print("GPUs Available:", tf.config.list_physical_devices('GPU'))

# TensorFlow automatically uses available GPUs
with tf.device('/GPU:0'):  # Explicitly specify GPU if multiple are available
   # Computation runs on GPU if available
   result = tf_model.predict(X_tf)

5. Hardware especializado

Além das GPUs, hardwares como as unidades de processamento de tensores (TPUs) do Google são projetados especificamente para operações de redes neurais.

6. Otimizações algorítmicas

Determinadas funções de ativação e arquiteturas de rede são projetadas para aumentar a eficiência computacional:

• O ReLU é mais rápido de calcular do que o sigmoide ou o tanh.
• As convoluções separáveis em profundidade reduzem a computação em comparação com as convoluções padrão.
• A poda de rede remove conexões desnecessárias, reduzindo a computação.

7. Otimizações de estrutura

As estruturas de aprendizagem profunda implementam várias otimizações de baixo nível:

• As operações fundidas combinam várias etapas em núcleos de otimização única.
• Os algoritmos com ajuste automático selecionam a implementação mais rápida para um hardware específico.
• A compilação JIT (Just-In-Time) cria um código otimizado para configurações de rede específicas.

À medida que as redes se tornam mais profundas e amplas, a otimização da propagação direta se torna cada vez mais importante. Arquiteturas modernas, como ResNets, Transformers e EfficientNets, incorporam opções de design especificamente para tornar a propagação direta mais eficiente e, ao mesmo tempo, manter ou melhorar a precisão do modelo.

Na próxima seção, exploraremos como a propagação para frente se conecta à propagação para trás (backpropagation), completando o quadro de como as redes neurais aprendem.

A relação com a retropropagação

Já exploramos a propagação direta de forma completa, mas isso é apenas metade da história quando se trata de redes neurais. Vamos examinar brevemente como a propagação direta se conecta com a retropropagação, o algoritmo que permite que as redes neurais aprendam.

Conectando a propagação para frente e para trás

A propagação direta e a retropropagação funcionam como processos complementares nas redes neurais:

• Propagação direta recebe entradas e produz previsões, movendo-se da esquerda para a direita na rede.
• Retropropagação recebe erros e produz atualizações de peso, movendo-se da direita para a esquerda na rede.

Esses dois processos são inseparáveis no processo de aprendizagem. A retropropagação não pode ocorrer sem que você execute primeiro a propagação direta, conforme necessário:

1. As ativações de cada camada (que armazenamos em nossos caches).
2. A previsão final a ser comparada com o rótulo verdadeiro.
3. A arquitetura da rede e os pesos usados durante a propagação direta.

Pense na propagação direta como uma rede neural que faz sua melhor suposição, considerando sua compreensão atual, enquanto a retropropagação é como ela refina essa compreensão com base em seus erros.

O ciclo de aprendizagem

Todo o processo de aprendizado segue um padrão cíclico:

1. Propagação direta: A rede processa os dados de entrada e faz previsões.
2. Cálculo de perdas: As previsões são comparadas com os alvos reais para calcular o erro.
3. Propagação para trás: O erro é propagado para trás na rede para determinar como cada peso contribuiu para o erro.
4. Atualização de peso: Os pesos são ajustados para reduzir o erro.
5. Repita: O processo continua com novos dados até que a rede tenha um bom desempenho.

O que torna esse processo poderoso é o fato de a propagação progressiva fornecer o contexto necessário para a retropropagação. Durante a propagação direta, a rede não só faz previsões, mas também mantém o controle de todos os valores e decisões intermediários. Em seguida, a retropropagação usa essas informações para fazer ajustes direcionados.

A beleza desse sistema é que a aprendizagem complexa emerge desses dois processos relativamente simples que trabalham juntos. A propagação direta é simples: são apenas multiplicações de matrizes e funções de ativação aplicadas sequencialmente. A retropropagação é mais complexa, mas decorre diretamente dos princípios de cálculo.

Juntos, eles permitem que as redes neurais aprendam praticamente qualquer padrão com dados e recursos computacionais suficientes. Essa capacidade de aprendizado impulsionou avanços na visão computacional, no processamento de linguagem natural, em jogos e em inúmeros outros domínios.

Compreender completamente a propagação direta, como fizemos neste artigo, fornece a base necessária para que você compreenda todo o processo de aprendizagem em redes neurais. Se você estiver interessado em se aprofundar no aspecto do aprendizado, nosso guia sobre retropropagação oferece uma exploração detalhada de como as redes aprendem com seus erros.

Conclusão e próximas etapas

A propagação direta é o processo fundamental que permite que as redes neurais transformem entradas em previsões. Como já exploramos, ele envolve multiplicações sequenciais de matrizes e funções de ativação que transformam progressivamente os dados por meio das camadas da rede. Compreender esse processo é fundamental se você estiver implementando redes do zero, usando estruturas modernas ou solucionando problemas de desempenho do modelo. 

Ao dominar a propagação progressiva, você deu um passo significativo em direção à criação e à compreensão de modelos de aprendizagem profunda que podem resolver problemas complexos em vários domínios.

Para continuar sua jornada de aprendizagem profunda, explore os recursos abrangentes do DataCamp: 

• Mergulhe na matemática por trás das redes neurais com Introdução às redes neurais profundas
• Domine o processo de treinamento com Dominando a retropropagação
• Obtenha experiência prática na criação de redes com o PyTorch ou R.

Para que você tenha um caminho de aprendizagem estruturado, a Aprendizagem profunda em Python oferece tudo o que você precisa para se tornar proficiente na criação e implementação de redes neurais para aplicativos do mundo real.