Course
Accurately preparing your data is important both for the performance of models and the interpretation of the results. This is the central challenge where normalization and standardization come in - two essential feature scaling techniques that can be used to adjust data for better performance or help in the interpretation of results.
In this article, I will walk you through the different terms and also help you see something of the practical differences between normalization and standardization. By the end, you will understand when to use each in your data preprocessing workflow. By becoming familiar with normalization and standardization, you will boost the performance of your models, better interpret the results, and avoid common pitfalls that come with unscaled data. The subtle differences here are very important in the field of machine learning. If you are serious about becoming an expert, enroll in our Machine Learning Scientist in Python career track today.
Become an ML Scientist
Understanding Feature Scaling
Normalization and standardization both belong to the idea or category of feature scaling. Feature scaling is an important step in preparing data for machine learning models. It involves transforming the values of features in a dataset to a similar scale, ensuring that all features contribute equally to the model’s learning process.
Feature scaling is important because, when features are on vastly different scales, like a feature ranging from 1 to 10 and another from 1,000 to 10,000, models can prioritize the larger values, leading to bias in predictions. This can result in poor model performance and slower convergence during training.
Feature scaling addresses these issues by adjusting the range of the data without distorting differences in the values. There are several scaling techniques, with normalization and standardization being the most commonly used. Both methods help machine learning models perform optimally by balancing the impact of features, reducing the influence of outliers, and, in some cases, improving convergence rates.
What is Normalization?
Normalization is a broad idea, and there are different ways to normalize data. Generally speaking, normalization refers to the process of adjusting values measured on different scales to a common scale. Sometime's, it's best to illustrate with an example. For each type of normalization below, we will consider a model to understand the relationship between the price of a house and its size.
Types of normalization
Let's look at some of the main types. Keep in mind, this is not a comprehensive list:
Min-max normalization
With min-max normalization, we might rescale the sizes of the houses to fit within a range of 0 to 1. This means that the smallest house size would be represented as 0, and the largest house size would be represented as 1.
Log normalization
Log normalization is another normalization technique. By using log normalization, we apply a logarithmic transformation to the house prices. This technique helps reduce the impact of larger prices, especially if there are significant differences between them.
Decimal scaling
Decimal scaling is another normailzation technique. For this example, we might adjust the sizes of the houses by shifting the decimal point to make the values smaller. This means that the house sizes are transformed to a more manageable scale while keeping their relative differences intact.
Mean normalization (mean-centering)
Mean normalization, in this context, would involve adjusting the house prices by subtracting the average price from each house's price. This process centers the prices at zero, showing how each house's size compares to the average. By doing this, we can analyze which house sizes are larger or smaller than average, making it easier to interpret their relative prices.
When should you normalize data?
As you may have inferred from the above examples, normalization is particularly useful when the distribution of the data is unknown or does not follow a Gaussian distribution. House prices are a good example here because some houses are very, very expensive, and models don’t always deal well with outliers.
So, the goal of normalization is to make a better model. We might normalize the dependent variable so the errors are more evenly distributed, or else we might normalize the input variables to ensure that features with larger scales do not dominate those with smaller scales.
Normalization is most effective in the following scenarios:
- Unknown or Non-Gaussian Distribution: When the distribution of data is not known or does not follow a normal (Gaussian) pattern. For example in linear regression, we may want to normalize the dependent variable so it looks more like a bell curve, which allows for better confidence in our estimates.
- Distance-Based Algorithms: Normalization is needed when using machine learning algorithms that rely on distances between data points, such as k-Nearest Neighbors (k-NN), to prevent features with larger scales from dominating the distance calculations.
What is Standardization?
While normalization scales features to a specific range, standardization, which is also called z-score scaling, transforms data to have a mean of 0 and a standard deviation of 1. This process adjusts the feature values by subtracting the mean and dividing by the standard deviation. You might have heard of ‘centering and scaling’ data. Well, standardization refers to the same thing: first centering, then scaling.
The formula for standardization is:
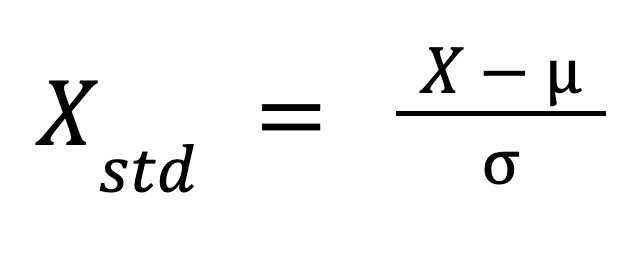
Where:
- X is the original value,
- mu is the mean of the feature, and
- sigma is the standard deviation of the feature.
This formula rescales the data in such a way that its distribution has a mean of 0 and a standard deviation of 1.
When should you standardize data?
Standardization is most appropriate in the following cases:
- Gradient-based Algorithms: Support Vector Machine (SVM) requires standardized data for optimal performance. While models like linear regression and logistic regression do not assume standardization, they may still benefit from it, particularly when features vary widely in magnitude, helping ensure balanced contributions from each feature and improving optimization.
- Dimensionality Reduction: Standardization is in dimensionality reduction techniques like PCA because PCA identifies the direction where the variance in the data is maximized. Mean normalization alone is not sufficient because PCA considers both the mean and variance, and different feature scales would distort the analysis.
Normalization vs. Standardization: Key Differences
Sometimes, it’s difficult to distinguish between normalization and standardization. For one thing, normalization is sometimes used as a more general term, while standardization has a meaning that is a little more specific or specifically technical. Also, data analysts and data scientists who are familiar with the terms might still struggle to distinguish use cases.
While both are feature scaling techniques, they differ in their approaches and applications. Understanding these differences is key to choosing the right technique for your machine learning model.
Rescaling methods
Normalization rescales feature values within a predefined range, often between 0 and 1, which is particularly useful for models where the scale of features varies greatly. In contrast, standardization centers data around the mean (0) and scales it according to the standard deviation (1).
Sensitivity to outliers
Different normalization techniques vary in their effectiveness at handling outliers. Mean normalization can successfully adjust for outliers in some scenarios, but other techniques might not be as effective. In general, normalization techniques do not handle the outlier problem as effectively as standardization because standardization explicitly relies on both the mean and the standard deviation.
Use cases
Normalization is widely used in distance-based algorithms like k-Nearest Neighbors (k-NN), where features must be on the same scale to ensure accuracy in distance calculations. Standardization, on the other hand, is vital for gradient-based algorithms such as Support Vector Machines (SVM) and is frequently applied in dimensionality reduction techniques like PCA, where maintaining the correct feature variance is important.
Summary table of differences
Let’s look at all these key differences in a summary table to make it easier to compare normalization and standardization:
| Category | Normalization | Standardization |
|---|---|---|
| Rescaling Method | Scales data to a range (usually 0 to 1) based on minimum and maximum values. | Centers data around the mean (0) and scales it by the standard deviation (1). |
| Sensitivity to outliers | Normalization can help adjust for outliers if used correctly, depending on the technique. | Standardization is a more consistent approach to fixing outlier problems. |
| Common Algorithms | Often applied in algorithms like k-NN and neural networks that require data to be on a consistent scale. | Best suited for algorithms that require features to have a common scale, such as logistic regression, SVM, and PCA. |
Visualizing the Differences
To understand the differences between normalization and standardization, it is helpful to see their effects visually and in terms of model performance. Here, I have included boxplots to show these different feature scaling techniques. Here, I have used min-max normalization on each of the variables in my dataset. We can see that no value is lower than 0 or bigger than 1.
Normalized data. Image by Author
In this second visual, I have used standardization on each of the variables. We can see that the data is centered at zero.
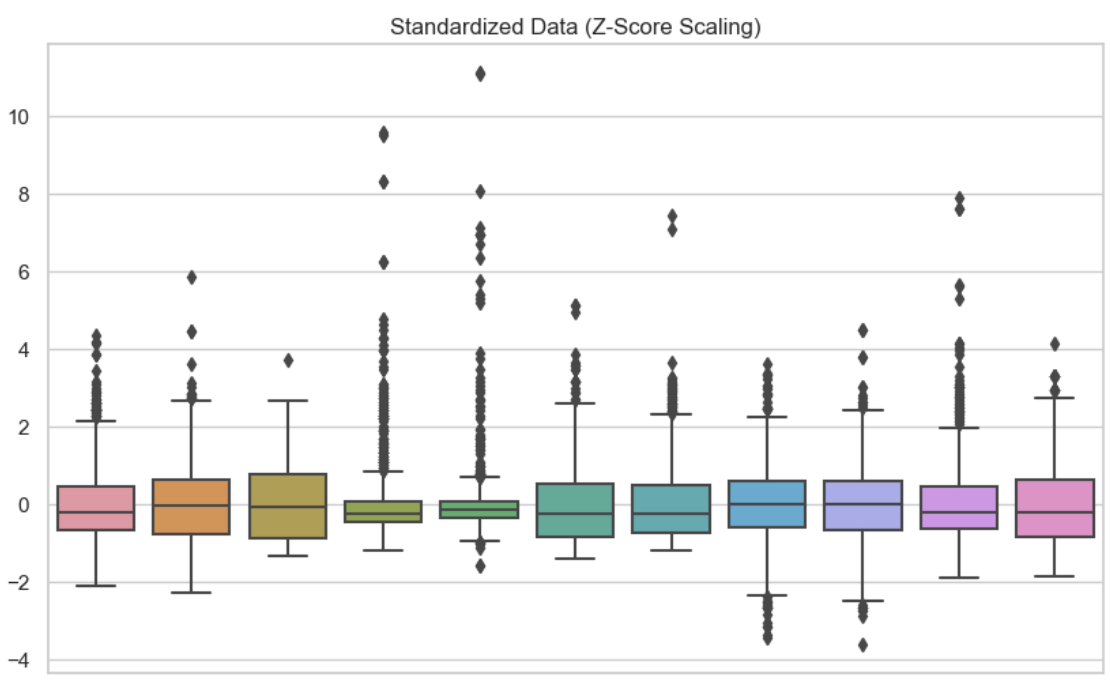 Standardized data. Image by Author
Standardized data. Image by Author
Advantages and disadvantages
The advantages include improved model performance and balanced feature contributions. However, normalization can limit interpretability due to the fixed scale, while standardization can also make interpretation harder as the values no longer reflect their original units. There’s always a trade-off between model complexity and model accuracy.
Normalization and Standardization in Linear Regression
Let’s consider how normalization (in this case, mean normalization) and standardization might change the interpretation of a simple linear regression model. The R-squared or adjusted R-squared would be the same for each model, so the feature scaling here is only about the interpretation of our model.
| Transformation Applied | Independent Variable (House Size) | Dependent Variable (House Price) | Interpretation |
|---|---|---|---|
| Mean Normalization | Mean Normalized | Original | You are predicting the original house price for each change in house size relative to the average. |
| Standardization | Standardized | Original | You are predicting the original house price for each one standard deviation change in house size. |
| Mean Normalization | Original | Mean Normalized | You are predicting the house price relative to the average for each one-unit increase in the original house size. |
| Standardization | Original | Standardized | You are predicting the standardized house price for each one-unit increase in the original house size. |
| Mean Normalization (Both Variables) | Mean Normalized | Mean Normalized | You are predicting the house price relative to the average for each change in house size relative to the average. |
| Standardization (Both Variables) | Standardized | Standardized | You are predicting the standardized house price for each one standard deviation change in house size. |
As another important note, in linear regression, if you standardize the independent and dependent variables, the r-squared will stay the same. This is because r-squared measures the proportion of the variance in y that is explained by x, and this proportion remains the same regardless of whether the variables are standardized or not. However, standardizing the dependent variable will change the RMSE, because RMSE is measured in the same units as the dependent variable. Since y is now standardized, the RMSE will be lower after standardization. Specifically, it will reflect the error in terms of the standard deviation of the standardized variable, not the original units. If regression is especially interesting to you, take our Introduction to Regression with statsmodels in Python course to become an expert.
Conclusion
Feature scaling, which includes normalization and standardization, is a critical component of data preprocessing in machine learning. Understanding the appropriate contexts for applying each technique can significantly enhance the performance and accuracy of your models.
If you are looking to expand and deepen your understanding of feature scaling and its role in machine learning, we have several excellent resources at DataCamp that can get you started. You can explore our article on Normalization in Machine Learning for foundational concepts, or consider our End-to-End Machine Learning course, covering real applications.
Become an ML Scientist
Experienced data professional and writer who is passionate about empowering aspiring experts in the data space.