Poisson Distribution: A Comprehensive Guide

In statistics and data science, the Poisson distribution is an important tool for modeling discrete events occurring within a fixed interval. Named after French mathematician Siméon Denis Poisson, this probability distribution helps analyze and predict rare events, making it valuable for data practitioners in various fields.

If you're new to statistics, our Introduction to Statistics course provides a solid foundation for grasping these concepts. For those ready to really learn probability theory, the Foundations of Probability in Python course offers a comprehensive exploration of probabilistic concepts, including the Poisson distribution. 

What is a Poisson Distribution?

The Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space. It assumes these events happen with a known average rate and independently of the time since the last event. To understand the Poisson distribution, it's first helpful to know the difference between discrete and continuous distributions.

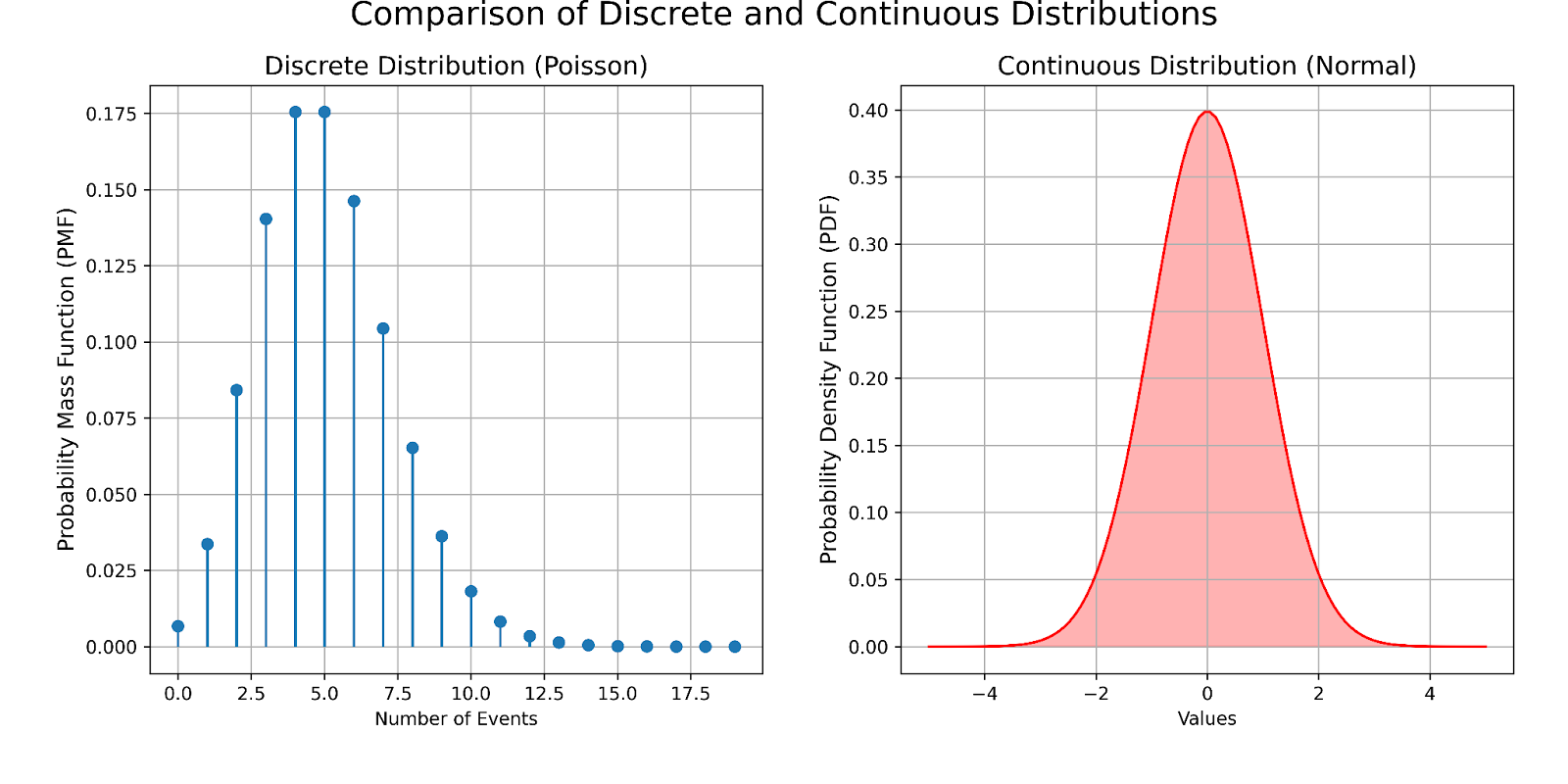
Poisson distribution vs. a continuous distribution. Image by Author

Discrete distributions

• Nature: Discrete distributions describe phenomena where outcomes can be counted in whole numbers. They are characterized by probability mass functions (PMF) that assign a probability to each possible discrete outcome.
• Visualization: In the left panel, the Poisson distribution is shown where each dot represents the probability of a specific number of events occurring within a fixed interval. This distribution is ideal for modeling count data, such as the number of emails received per hour. You might notice, also, that there are no negative values in the Poisson distribution panel. This is because Poisson distributions, by definition, can’t have negative values.

Some examples of discrete probability distributions include the Bernoulli and binomial distributions. 

Continuous distributions

• Nature: Continuous distributions are used for data that can take any value within a range, including decimals. They use probability density functions (PDF) to describe the probabilities of outcomes within any given range.
• Visualization: The right panel illustrates the normal distribution. The smooth curve indicates the density of values around the mean, and the area under the curve between any two points gives the probability of falling within that range. This type of distribution is useful for measuring quantities like temperature or weight.

The normal, or Gaussian, distribution is a prime example of a continuous distribution.

Properties of Poisson Distributions

Let’s look at some of the important characteristics of the Poisson distribution.

Events in a fixed interval

A key characteristic of the Poisson distribution is its ability to model events in a fixed interval. This interval can be time (e.g., number of customers arriving per hour) or space (e.g., number of defects per square meter of fabric). The model assumes:

1. Events occur independently.
2. The average rate of occurrence (λ) remains constant over the interval.
3. Two events cannot occur at exactly the same instant.

Mean and variance

One of the most distinctive properties of the Poisson distribution is that its mean (expected value) is equal to its variance. Both are represented by the parameter λ (lambda), which denotes the average number of events in the interval. This property is unique and helps in identifying whether a dataset follows a Poisson distribution. Mathematically, this can be represented in the following equation: 

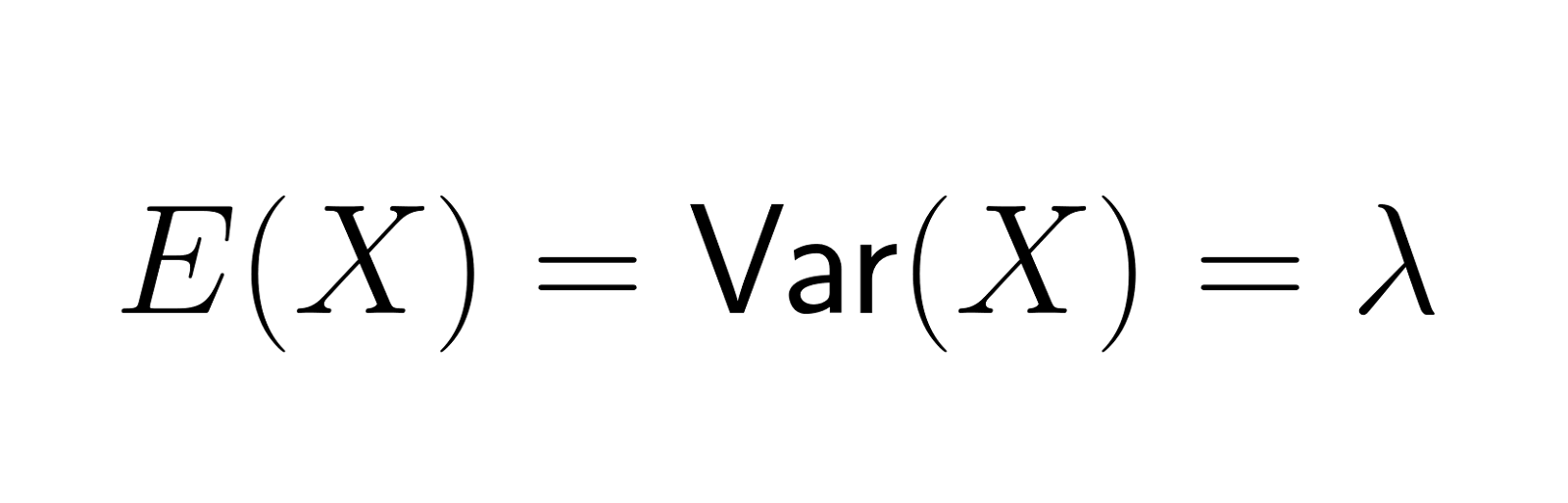
This equality implies that as the expected number of events increases, so does the variability in the actual number of occurrences.

Skewness and shape

The shape of the Poisson distribution varies based on the value of λ. This visual illustration demonstrates how λ affects the skewness and symmetry of the distribution: 

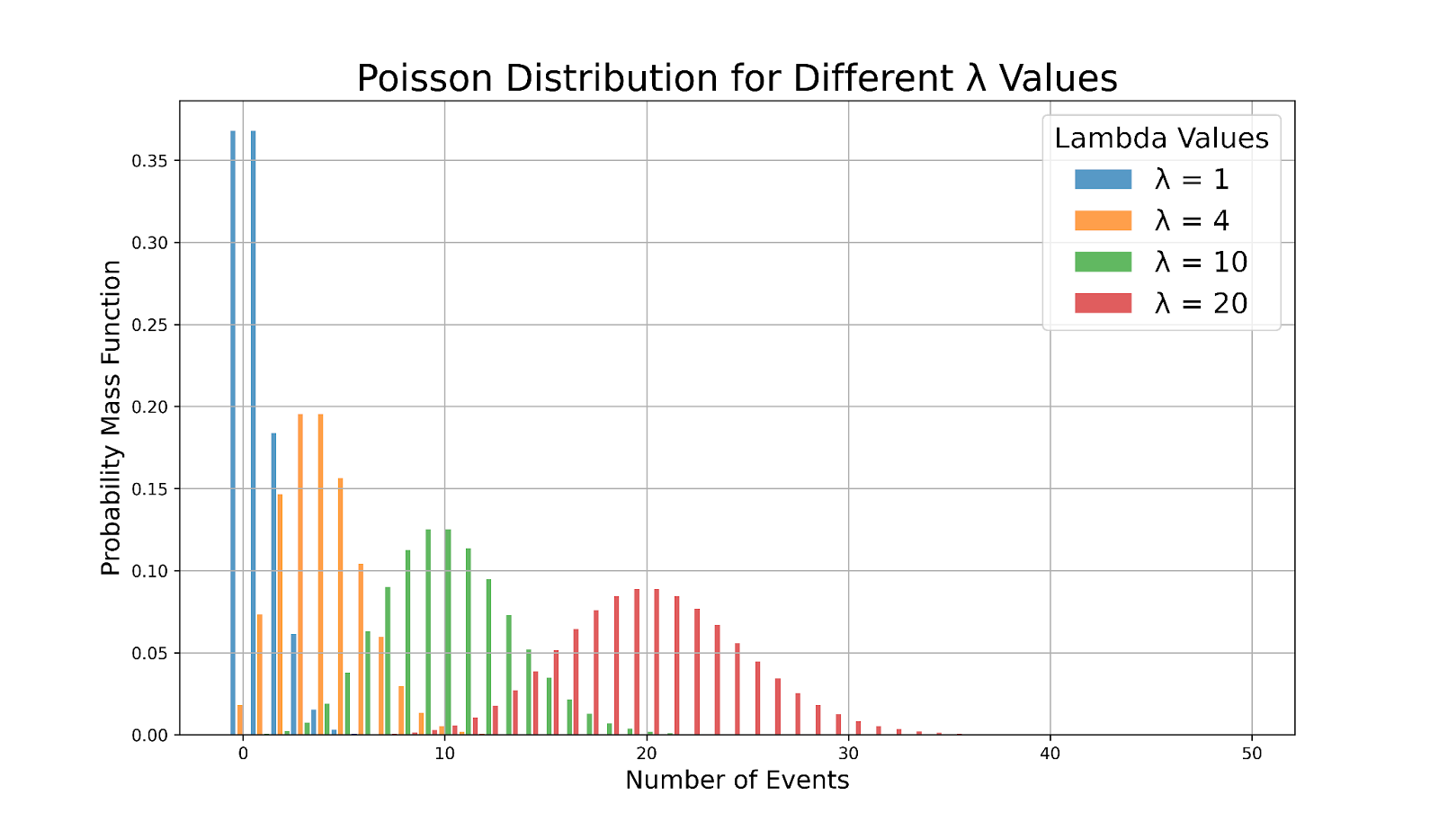
Poisson distributions with different lambda values. Image by Author

• For small λ values (λ < 10), the distribution is noticeably right-skewed. This means that there are more occurrences with fewer events and fewer occurrences with a larger number of events.
• As λ increases (λ > 10), the distribution becomes more symmetric and starts to resemble a normal distribution. This symmetry indicates that the data is more evenly distributed around the mean.

This changing shape affects how we interpret probabilities and make inferences from Poisson-distributed data. For instance, a symmetric distribution simplifies many types of analyses, such as hypothesis testing and confidence interval estimation, because the data's distribution is more predictable and balanced.

Poisson Distribution Formula

Take a look at the Poisson distribution formula. 

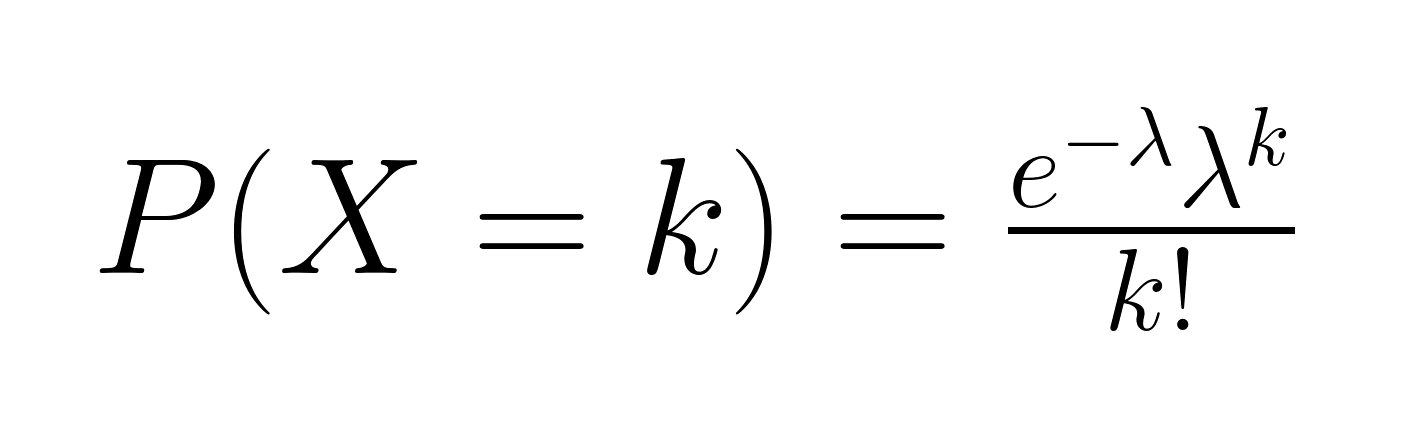
• The left-hand side (LHS) of the Poisson distribution formula, P(X = k), represents the probability of exactly k events occurring within a fixed interval. Here, X is the number of events, and k is the specific number we’re interested in. In other words, the LHS tells us what probability we’re calculating.

• The numerator on the right-hand side (RHS), e^-λλ^k has two parts. λ^k shows how likely it is for k events to happen based on the average rate λ. The e^-λ term accounts for the randomness of the events, ensuring the probability decreases as the number of events deviates from the expected rate.

• The denominator on the right-hand side (RHS), k! adjusts for how many ways the x events can occur. Factorial notation calculates the number of possible arrangements, making sure the probability reflects the fact that the order of events doesn’t matter.

If you really want to become confident in using Python for machine learning, start our Machine Learning Scientist with Python career track, which lets you practice advanced techniques with real data sets.