Varianz-Inflations-Faktor (VIF): Umgang mit Multikollinearität in der Regressionsanalyse

Was ist der Varianz-Inflations-Faktor (VIF)?

Der von dem Statistiker Cuthbert Daniel entwickelte VIF ist ein weit verbreitetes Diagnoseinstrument in der Regressionsanalyse, um Multikollinearität zu erkennen, die bekanntermaßen die Stabilität und Interpretierbarkeit von Regressionskoeffizienten beeinträchtigt. Technisch gesehen quantifiziert der VIF, wie stark die Varianz eines Regressionskoeffizienten aufgrund von Korrelationen zwischen den Prädiktoren erhöht ist.

All das ist wichtig, denn diese Korrelationen erschweren es, den einzigartigen Effekt der einzelnen Prädiktoren auf die Zielvariable zu isolieren, was zu weniger zuverlässigen Modellschätzungen führt. Ich sollte noch erwähnen, dass der VIF immer für jeden Prädiktor in einem Modell berechnet wird , um die richtige Geschichte zu erzählen .

Die Formel für den Varianz-Inflationsfaktor

Der VIF für einen Prädiktor X wird wie folgt berechnet:

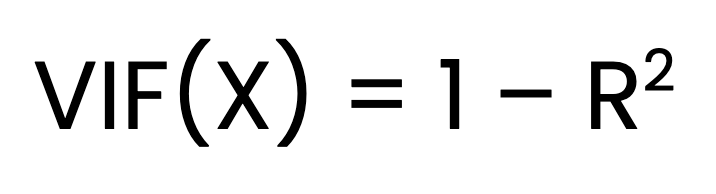
Wo:

• ^R2 ist der Bestimmungskoeffizient, den man erhält, wenn X​ wird auf alle anderen Prädiktoren regressiert.

Schritt-für-Schritt-Berechnung

Die Ermittlung der VIF erfolgt in drei Schritten. Der erste Schritt besteht darin, für jeden Prädiktor ein eigenes lineares Regressionsmodell gegen alle anderen Prädiktoren anzuwenden. Der zweite Schritt besteht darin, den^R2 Wert für jedes Modell zu ermitteln. Der letzte Schritt ist die Berechnung des VIF mit Hilfe der oben genannten Formel.

Interpretation der VIF-Werte

Hier erfährst du, wie du die VIF-Werte interpretierst, um den Grad der Multikollinearität zu verstehen:

• VIF = 1: Dies zeigt, dass keine Multikollinearität vorliegt. Der Prädiktor ist nicht mit anderen Prädiktoren korreliert, sodass er den Standardfehler nicht aufbläht oder die Stabilität des Modells beeinträchtigt.
• VIF zwischen 1 und 5: Dies deutet auf eine moderate Multikollinearität hin. Es gibt eine gewisse Korrelation mit anderen Prädiktoren, aber die ist in der Regel nicht gravierend. Es lohnt sich jedoch, diese Prädiktoren im Auge zu behalten, um zu sehen, ob Multikollinearität zu einem Problem wird, insbesondere wenn andere VIF-Werte hoch sind.
• VIF > 5: Es liegt eine hohe Multikollinearität vor. Der Standardfehler des Prädiktors kann deutlich überhöht sein, was seinen Koeffizienten weniger zuverlässig machen kann. Erwäge Maßnahmen zur Verringerung der Multikollinearität, wie das Entfernen oder Kombinieren korrelierter Prädiktoren.
• VIF > 10: Dies deutet auf eine ernsthafte Multikollinearität hin. Der Standardfehler des Prädiktors ist stark aufgebläht, und die Koeffizientenschätzung ist wahrscheinlich instabil. In der Regel sind Korrekturmaßnahmen wie das Entfernen des Prädiktors oder der Einsatz von Regularisierungstechniken erforderlich.

Wenn der VIF eines Prädiktors beispielsweise 10 beträgt, bedeutet dies, dass die Varianz des Koeffizienten dieses Prädiktors zehnmal so hoch ist, wie sie es wäre, wenn keine Multikollinearität vorliegen würde. 

Wie der VIF die Multikollinearität in der Regression erklärt

Multikollinearität führt dazu, dass sich die Standardfehler erhöhen, was es schwieriger macht, die Signifikanz der einzelnen Prädiktoren zu beurteilen. Dies liegt daran, dass kollineare Variablen ähnliche Informationen enthalten, was es schwierig macht, ihre spezifischen individuellen Auswirkungen auf die Ergebnisvariable zu trennen. 

Multikollinearität beeinträchtigt zwar nicht unbedingt die Vorhersagekraft des Modells, aber sie verringert die Zuverlässigkeit und Klarheit der Koeffizienten. Das ist besonders dann problematisch, wenn wir die individuellen Auswirkungen der einzelnen Prädiktoren verstehen wollen.

Der Varianzinflationsfaktor (VIF) dient als präzises diagnostisches Maß zur Identifizierung von Multikollinearität. Im Gegensatz zu allgemeinen Beobachtungen über die Korrelation isoliert der VIF die kombinierte Wirkung aller Prädiktoren auf jede Variable und hebt Wechselwirkungen hervor, die aus paarweisen Korrelationen möglicherweise nicht ersichtlich sind.

Variance Inflation Factor in Python und R

Um das zu verdeutlichen, gehen wir ein Beispiel in Python und R durch und verwenden dabei einen einzigartigen Datensatz. Wir werden den VIF mit automatisierten Paketen berechnen und auch die VIF-Formel verwenden, um eine Intuition zu entwickeln. Um eine gute Übung zu haben, habe ich absichtlich einen Datensatz erstellt, bei dem wir einen hohen VIF-Wert für eine unserer Variablen entdecken werden, obwohl es keine sehr hohe paarweise Korrelation zwischen zwei Variablen gibt - ich denke, das ist ein überzeugendes Beispiel. Beginnen wir mit einem Überblick über den Datensatz, den wir verwenden werden.

Datensatz-Übersicht:

Dieser fiktive Datensatz stellt die Umfrageergebnisse einer Studie dar, die in 1.000 Filialen eines Einzelhandelsriesen durchgeführt wurde. Die Kunden in jedem Laden wurden gebeten, verschiedene Aspekte ihres Einkaufserlebnisses auf einer Skala von -5 bis +5 zu bewerten, wobei -5 für ein sehr negatives Erlebnis und +5 für ein sehr positives Erlebnis steht. Der Durchschnitt der Kundenbewertungen in jedem Laden wurde für vier Schlüsselparameter ermittelt:

• Ambience: Die Kunden nehmen die Umgebung des Ladens wahr, z. B. die Sauberkeit, die Einrichtung, die Beleuchtung und die allgemeine Atmosphäre. 

• Customer_service: Bewertung des Service durch das Ladenpersonal, einschließlich Hilfsbereitschaft, Freundlichkeit und Eingehen auf die Bedürfnisse der Kunden.

• Offers: Bewertung der Sonderangebote, Rabatte und Deals des Ladens, die den Kunden zur Verfügung stehen.

• Product_range: Bewertung der Vielfalt und Qualität der im Laden erhältlichen Produkte.

Die Zielvariable, Performance, misst die Gesamtleistung jedes Marktes. Aus der VIF-Perspektive ist das jedoch nicht relevant. Du kannst den Datensatz hier herunterladen. 

Varianz-Inflationsfaktor in Python

Wir beginnen mit der Berechnung der VIF-Werte mithilfe der Python-Pakete. Der erste Schritt besteht darin, den Datensatz und die benötigten Bibliotheken zu laden. 

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant

datacamp_retail_data = pd.read_csv(' vif_data.csv')
datacamp_retail_data.head()

Der obige Code lädt die Daten und zeigt die ersten fünf Datensätze an. 

In einem nächsten Schritt können wir eine Korrelationsmatrix erstellen, um die paarweise Korrelation zu überprüfen.

Der folgende Code wählt vier Spalten aus und speichert sie in einem neuen DataFrame namens correl_data . Anschließend wird die paarweise Korrelationsmatrix mit der Funktion .corr() berechnet. Das Ergebnis wird im Objekt corr_matrix gespeichert, das eine Tabelle mit den Korrelationskoeffizienten zwischen jedem Paar der ausgewählten Spalten darstellt. 

Die Matrix wird dann mit der Funktion heatmap() von Seaborn visualisiert. Dabei wird jeder Korrelationskoeffizient als farbkodierte Zelle angezeigt, wobei Blau für negative Korrelationen und Rot für positive Korrelationen steht, basierend auf der coolwarm Farbkarte. 

correl_data = datacamp_retail_data[['Ambience', 'Customer_service', 'Offers', 'Product_range']]

# Compute the pairwise correlation matrix
corr_matrix = correl_data.corr()

# Visualize the correlation matrix
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('Pairwise Correlation Matrix')
plt.show()

Ausgabe:

  Korrelation zwischen den Variablen. Bild vom Autor

Der Plot bietet eine visuelle Zusammenfassung der Beziehungen zwischen den Variablen in correl_data. Die Korrelationswerte reichen von -1 bis 1. Werte, die näher an 1 liegen, weisen auf eine starke positive Korrelation hin, Werte, die näher an -1 liegen, auf eine starke negative Korrelation und Werte um 0 auf keine Korrelation. Es ist offensichtlich, dass es keine starke paarweise Korrelation zwischen den Variablen gibt, da keiner der Korrelationswerte größer als 0,6 ist. 

Der nächste Schritt ist die Berechnung der VIF-Werte für die Prädiktorvariablen. Der folgende Code berechnet die Werte für jede Prädiktorvariable im Datensatz, um auf Multikollinearität zu prüfen. 

Zunächst definiert sie X, indem sie die Zielspalte Performance entfernt und einen Intercept hinzufügt. Dann wird ein DataFrame datacamp_vif_data erstellt, in dem die Namen der Prädiktoren und ihre VIF-Werte gespeichert werden. In einer Schleife wird dann der VIF für jeden Prädiktor mit derFunktion variance_inflation_factor() berechnet, wobei höhere VIFs auf das Vorhandensein von Multikollinearität hinweisen .

# Define the predictor variables
X = datacamp_retail_data.drop(columns=['Performance'])

# Add a constant to the model (intercept)
X = add_constant(X)

# Calculate VIF for each feature
datacamp_vif_data = pd.DataFrame()
datacamp_vif_data['Feature'] = X.columns
datacamp_vif_data['VIF'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(datacamp_vif_data)

Ausgabe:

Die Ausgabe zeigt die VIF-Werte. Bild vom Autor

Diese Ausgabe zeigt den VIF-Wert für jede Prädikatorvariable an, der das Multikollinearitätsniveau im Datensatz angibt. Die Zeile const stellt den Intercept-Term dar, dessen VIF nahe bei 1 liegt, was bedeutet, dass er keine Multikollinearität aufweist. Von den Prädiktorvariablen hat Product_range die höchste VIF (5,94), was darauf hindeutet, dass sie korrigiert werden muss. Alle anderen Prädiktoren haben VIF-Werte unter 3, was auf eine geringe Multikollinearität hindeutet. 

Manueller Ansatz zur VIF-Berechnung

Die andere Methode besteht darin, die Werte separat zu berechnen, indem man jede unabhängige Variable gegen die anderen Prädiktorvariablen regressiert.  

Es funktioniert so, dass für jedes Merkmal in retail_data dieses Merkmal als abhängige Variable (y) und die übrigen Merkmale als unabhängige Variablen (X) festgelegt werden. Dann wird ein lineares Regressionsmodell angepasst, um y anhand von X vorherzusagen, und der R-Quadrat-Wert des Modells wird verwendet, um den VIF mithilfe der Formel zu berechnen, die wir im ersten Abschnitt erläutert haben.

Anschließend werden jedes Merkmal und die dazugehörigen VIF-Werte in einem Wörterbuch (vif_manual) gespeichert, das dann zur Anzeige in einen DataFrame (vif_manual_df) umgewandelt wird. 

datacamp_retail_data = retail_data.drop(columns=['Performance'])

# Manual VIF Calculation
vif_manual = {}

for feature in retail_data.columns:
    # Define the target variable (current feature) and predictors (all other features)
    y = datacamp_retail_data[feature]
    X = datacamp_retail_data.drop(columns=[feature])

    # Fit the linear regression model
    model = LinearRegression().fit(X, y)

    # Calculate R-squared
    r_squared = model.score(X, y)

    # Calculate VIF
    vif = 1 / (1 - r_squared)
    vif_manual[feature] = vif

# Convert the dictionary to a DataFrame for better display
vif_manual_df = pd.DataFrame(list(vif_manual.items()), columns=['Feature', 'VIF'])
print(vif_manual_df)

 Ausgabe:

Die Ausgabe zeigt die VIF-Werte. Bild vom Autor

Die Ausgabe zeigt jedes Merkmal zusammen mit seinem VIF-Wert an und hilft dabei, potenzielle Multikollinearitätsprobleme zu erkennen. Wie du siehst, ist das Ergebnis dasselbe wie oben und wird auch so interpretiert, nämlich dass die Variable Product_range Multikollinearität aufweist.

Varianz-Inflationsfaktor in R

In diesem Abschnitt wiederholen wir die Übung des obigen Varianzinflationsfaktors im Python-Abschnitt, insbesondere für Entwickler, die mit der Programmiersprache R arbeiten. Wir beginnen mit dem Laden des Datensatzes und der notwendigen Bibliotheken.

library(tidyverse)
library(car)
library(corrplot)

data <- read.csv('vif_data.csv')
str(data)

Ausgabe:

Im nächsten Schritt berechnest du die paarweise Korrelationsmatrix und visualisierst sie mit der Heatmap. Die Funktionen cor() und corrplot helfen uns, diese Aufgabe zu erfüllen.

# Remove the target column
predictors_data <- data[, !(names(data) %in% "Performance")]

# Calculate the correlation matrix
correlation_matrix <- cor(predictors_data)

# Plot the correlation heatmap
# Load necessary libraries
library(ggplot2)
library(reshape2)
melted_corr_matrix <- melt(correlation_matrix)

# Plot the heatmap with ggplot2
ggplot(data = melted_corr_matrix, aes(x = Var1, y = Var2, fill = value)) +
  geom_tile(color = "white") +
  scale_fill_gradient2(low = "blue", high = "red", mid = "white", 
                       midpoint = 0, limit = c(-1, 1), space = "Lab", 
                       name="Correlation") +
  theme_minimal() + # Minimal theme for a clean look
  theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1)) +
  labs(x = "", y = "") + # Remove axis labels
  geom_text(aes(Var1, Var2, label = round(value, 2)), color = "black", size = 4) +
  theme(axis.text=element_text(size=15))

Ausgabe:

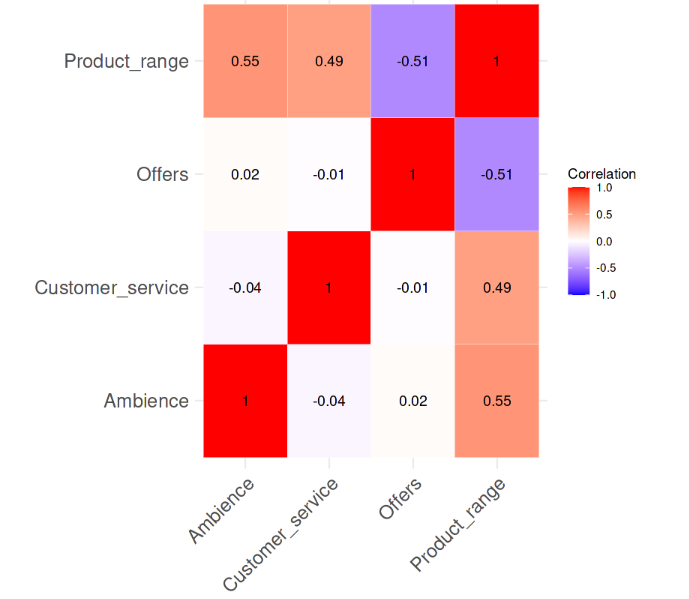
Korrelation zwischen den Variablen. Bild vom Autor

Aus der Korrelations-Heatmap geht hervor, dass es keine starke paarweise Korrelation zwischen den Variablen gibt, da keiner der Korrelationswerte größer als 0,6 ist. Jetzt berechnen wir die VIF-Werte und sehen, ob es etwas Alarmierendes gibt. Die folgende Code-Zeile erledigt diese Aufgabe. 

# Fit a regression model
model <- lm(Performance ~ Ambience + Customer_service + Offers + Product_range, data = data)

# Calculate VIF
vif(model)

Ausgabe:

Aus dem Ergebnis geht hervor, dass von den Prädiktorvariablen nur die Variable Product_range einen VIF-Wert von über 5 hat, was auf eine hohe Multikollinearität hindeutet, die korrigiert werden muss. 

Manueller Ansatz zur VIF-Berechnung

Der andere Ansatz zur VIF-Berechnung wäre, die VIF-Werte für jede Variable einzeln zu berechnen, indem man jede unabhängige Variable gegen die anderen Prädiktorvariablen regressiert.  

Dies wird im folgenden Code durchgeführt, der die Funktion sapply()für jeden Prädiktor verwendet, wobei jeder Prädiktor als abhängige Variable in einem linearen Regressionsmodell mit den anderen Prädiktoren als unabhängige Variablen festgelegt wird. 

Der R-Quadrat-Wert jedes Modells wird dann zur Berechnung der VIF-Werte mit der entsprechenden Formel verwendet. Das Ergebnis vif_values schließlich zeigt den VIF für jeden Prädiktor an und hilft dabei, Multikollinearitätsprobleme zu erkennen.

# VIF calculation for each predictor manually
predictors <- c("Ambience", "Customer_service", "Offers", "Product_range")

vif_values <- sapply(predictors, function(pred) {
    formula <- as.formula(paste(pred, "~ ."))
    model <- lm(formula, data = data[, predictors])
    1 / (1 - summary(model)$r.squared)
})

print(vif_values)

Ausgabe:

Wir erhalten das gleiche Ergebnis und es ist offensichtlich, dass die Variable Product_range mit einem hohen VIF-Wert über 5 ein Eingreifen erfordert. 

VIF vs. Korrelationsmatrix und andere Methoden

Zur Erinnerung: Hier sind die gängigen Methoden zur Erkennung von Multikollinearität:

• Hohe VIF-Werte: Ein hoher VIF-Wert ist ein klarer Indikator für Multikollinearität. Wenn diese Werte bestimmte Schwellenwerte überschreiten, zeigen sie an, dass ein Prädiktor stark mit anderen Prädiktoren zusammenhängt, was die Stabilität, Zuverlässigkeit und Leistung des Modells beeinträchtigen kann.
• Korrelationsmatrizen: Anhand einer Korrelationsmatrix kannst du die paarweisen Korrelationen zwischen den Prädiktoren erkennen. Hohe paarweise Korrelationen deuten auf Multikollinearität zwischen diesen spezifischen Prädiktoren hin. Diese Methode deckt jedoch nur direkte lineare Beziehungen zwischen zwei Variablen auf und kann Multikollinearität übersehen, die komplexere Wechselwirkungen zwischen mehreren Variablen beinhaltet.
• Koeffizientenänderungen: Wenn sich die Koeffizienten der Prädiktoren signifikant verändern, wenn du andere Variablen zum Modell hinzufügst oder entfernst, kann das ein Zeichen für Multikollinearität sein. Solche Schwankungen deuten darauf hin, dass bestimmte Prädiktoren gemeinsame Informationen teilen, was es schwieriger macht, den einzigartigen Einfluss jeder einzelnen Variable auf das Ergebnis zu ermitteln.

Unter all diesen Methoden ist der VIF besonders nützlich, weil er Multikollinearität auch dann aufdecken kann, wenn die paarweisen Korrelationen gering sind, wie wir in unserem Beispiel gesehen haben. Das macht die VIF zu einem umfassenderen Instrument.

Zusätzliche Ideen für den Umgang mit hohen VIF-Werten

Wenn die VIF-Werte auf eine hohe Multikollinearität hindeuten und du die Variable nicht unbedingt einfach entfernen willst, gibt es einige andere, fortschrittlichere Strategien, um die Multikollinearität abzuschwächen:

1. Feature Selection: Entferne einen der hoch korrelierten Prädiktoren und berechne den VIF neu, um zu sehen, ob das Modell dadurch vereinfacht und die Stabilität verbessert wird.
2. Hauptkomponentenanalyse (PCA): Nutze die PCA, um deine Prädiktoren zu einer kleineren Menge unkorrelierter Komponenten zu kombinieren. Dadurch werden die ursprünglichen Variablen in neue, unabhängige und unkorrelierte Variablen umgewandelt, die den größten Teil der Datenvariationen erfassen.
3. Regularisierungstechniken: Wende die Ridge- oder Lasso-Regression an, bei der das Modell um Strafterme ergänzt wird. Diese Techniken helfen, die Multikollinearität zu reduzieren, indem sie den Einfluss korrelierter Variablen verringern und das Modell stabiler und zuverlässiger machen.

Fazit

Die Kenntnis des VIF ist der Schlüssel zur Erkennung und Behebung von Multikollinearität, was die Genauigkeit und Klarheit von Regressionsmodellen verbessert. Die regelmäßige Überprüfung der VIF-Werte und die Anwendung von Korrekturmaßnahmen bei Bedarf hilft Datenexperten und Analysten, Modelle zu erstellen, denen sie vertrauen können. Dieser Ansatz stellt sicher, dass die Wirkung jedes einzelnen Prädiktors klar ist, so dass es einfacher ist, verlässliche Schlussfolgerungen aus dem Modell zu ziehen und bessere Entscheidungen auf der Grundlage der Ergebnisse zu treffen. Nimm an unserem Lernpfad für maschinelles Lernen in Python teil, um wirklich zu verstehen, wie man Modelle erstellt und sie einsetzt. Außerdem macht sich der Abschluss des Programms gut im Lebenslauf.

Wenn du dich weiterbilden möchtest, kannst du auch die folgenden Ressourcen aus dem DataCamp-Blog und den Tutorials nutzen:

• Grundlagen der linearen Regression in Python: Lerne, wie ein Regressionsproblem formuliert wird und wie ein linearer Regressionsalgorithmus in Python funktioniert.
• Wie man eine lineare Regression in R durchführt: Lerne die lineare Regression, ein statistisches Modell, das die Beziehung zwischen Variablen mit R analysiert.
• QR-Zerlegung beim maschinellen Lernen: Ein detaillierter Leitfaden: Lerne die QR-Zerlegung kennen, das Verfahren der Matrixfaktorisierung, bei dem die Matrix A in das Produkt einer orthogonalen Matrix Q und einer oberen Dreiecksmatrix R zerlegt wird.
• Lasso und Ridge Regression in Python Tutorial: Lerne die Lasso- und Ridge-Techniken der Regression kennen. Vergleiche und analysiere die Methoden im Detail.