Factor de Inflación de la Varianza (VIF): Cómo abordar la multicolinealidad en el análisis de regresión

¿Qué es el Factor de Inflación de la Varianza (VIF)?

Desarrollado por el estadístico Cuthbert Daniel, el VIF es una herramienta de diagnóstico muy utilizada en el análisis de regresión para detectar la multicolinealidad, que se sabe que afecta a la estabilidad e interpretabilidad de los coeficientes de regresión. Más técnicamente, el VIF funciona cuantificando cuánto se infla la varianza de un coeficiente de regresión debido a las correlaciones entre los predictores.

Todo esto es importante porque estas correlaciones dificultan el aislamiento del efecto único de cada predictor sobre la variable objetivo, lo que conduce a estimaciones del modelo menos fiables. También debo decir que, para contar realmente la historia correcta, el VIF siempre se calcula para cada predictor de un modelo.

La fórmula del factor de inflación de la varianza

El VIF de un predictor X se calcula como:

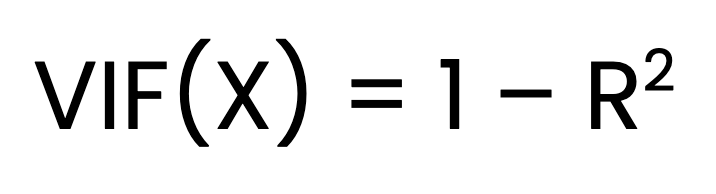
Dónde:

• ^R2 es el coeficiente de determinación obtenido cuando X​ se hace una regresión sobre todos los demás predictores.

Cálculo paso a paso

Encontrar el VIF es un proceso de tres pasos. El primer paso consiste en ajustar un modelo de regresión lineal independiente para cada predictor frente a todos los demás predictores. El segundo paso consiste en obtener el valor^R2 de cada modelo. El último paso es calcular el VIF utilizando la fórmula anterior.

Interpretación de los valores VIF

He aquí cómo interpretar los valores VIF para comprender el nivel de multicolinealidad:

• VIF = 1: Esto indica que no hay multicolinealidad. El predictor no está correlacionado con otros predictores, por lo que no infla el error típico ni afecta a la estabilidad del modelo.
• VIF entre 1 y 5: Esto sugiere una multicolinealidad moderada. Existe cierta correlación con otros predictores, pero no suele ser grave. Sin embargo, merece la pena vigilar estos predictores para ver si la multicolinealidad se convierte en un problema, sobre todo si otros valores VIF son altos.
• VIF > 5: Existe una alta multicolinealidad. El error típico del predictor puede estar notablemente inflado, lo que puede hacer que su coeficiente sea menos fiable. Considera la posibilidad de tomar medidas para reducir la multicolinealidad, como eliminar o combinar los predictores correlacionados.
• VIF > 10: Esto indica una multicolinealidad grave. El error típico del predictor está muy inflado y la estimación de su coeficiente es probablemente inestable. Suelen ser necesarias acciones correctoras, como eliminar el predictor o utilizar técnicas de regularización.

Por ejemplo, si el VIF de un predictor es 10, indica que la varianza del coeficiente de ese predictor es 10 veces mayor de lo que sería si no hubiera multicolinealidad. 

Cómo explica el VIF la multicolinealidad en la regresión

La multicolinealidad hace que aumenten los errores estándar, lo que dificulta la evaluación de la importancia de los predictores individuales. Esto ocurre porque las variables colineales llevan información similar, lo que dificulta separar sus efectos individuales específicos sobre la variable de resultado. 

Aunque la multicolinealidad no perjudica necesariamente la capacidad de predicción del modelo, sí reduce la fiabilidad y claridad de los coeficientes. Esto es especialmente problemático cuando queremos comprender el impacto individual de cada predictor.

El factor de inflación de la varianza (VIF) sirve como métrica diagnóstica precisa para identificar la multicolinealidad. A diferencia de las observaciones generales sobre la correlación, el VIF aísla el efecto combinado de todos los predictores sobre cada variable, destacando las interacciones que podrían no ser evidentes a partir de las correlaciones por pares.

Factor de Inflación de la Varianza en Python y R

Para que esto sea factible, veamos un ejemplo tanto en Python como en R utilizando un conjunto de datos único. Calcularemos el VIF utilizando paquetes automatizados y también utilizando la fórmula VIF para construir la intuición. Para tener una buena práctica, he creado deliberadamente un conjunto de datos en el que descubriremos un valor VIF alto para una de nuestras variables aunque no haya una correlación por pares muy alta entre ninguna de las dos variables, por lo que creo que es un ejemplo convincente. Empecemos con una visión general del conjunto de datos que vamos a utilizar.

Visión general del conjunto de datos:

Este conjunto de datos ficticio representa los resultados de un estudio realizado en 1.000 tiendas de un gigante minorista. Se pidió a los clientes de cada tienda que valoraran diversos aspectos de su experiencia de compra en una escala de -5 a +5, donde -5 indica una experiencia muy negativa, y +5 indica una experiencia muy positiva. Se tomó la media de las valoraciones de los clientes de cada tienda en cuatro parámetros clave:

• Ambience: Percepción de los clientes del entorno de la tienda, como la limpieza, la distribución, la iluminación y el ambiente general. 

• Customer_service: Valoración del servicio prestado por el personal de la tienda, incluida la amabilidad, la simpatía y la capacidad de respuesta a las necesidades del cliente.

• Offers: Valoración de las ofertas promocionales, descuentos y ofertas de la tienda disponibles para los clientes.

• Product_range: Evaluación de la variedad y calidad de los productos disponibles en la tienda.

La variable objetivo, Performance, mide el rendimiento global de cada tienda. Sin embargo, no es relevante desde el punto de vista del VIF. Puedes descargar el conjunto de datos aquí. 

Factor de inflación de la varianza en Python

Empezaremos calculando los valores VIF utilizando los paquetes python. El primer paso es cargar el conjunto de datos y las bibliotecas necesarias. 

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant

datacamp_retail_data = pd.read_csv(' vif_data.csv')
datacamp_retail_data.head()

El código anterior cargará los datos y mostrará los cinco primeros registros. 

Como paso siguiente, podemos ejecutar una matriz de correlaciones para comprobar la correlación entre pares.

El código siguiente selecciona cuatro columnas y las almacena en un nuevo DataFrame llamado correl_data . A continuación, calcula la matriz de correlaciones por pares mediante la función .corr(). El resultado se almacena en el objeto corr_matrix, que es una tabla que muestra los coeficientes de correlación entre cada par de las columnas seleccionadas. 

A continuación, la matriz se visualiza mediante la función heatmap() de Seaborn, mostrando cada coeficiente de correlación como una celda codificada por colores, en la que el azul representa correlaciones negativas y el rojo correlaciones positivas, según el mapa de colores coolwarm. 

correl_data = datacamp_retail_data[['Ambience', 'Customer_service', 'Offers', 'Product_range']]

# Compute the pairwise correlation matrix
corr_matrix = correl_data.corr()

# Visualize the correlation matrix
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('Pairwise Correlation Matrix')
plt.show()

Salida:

  Correlación entre las variables. Imagen del autor

El gráfico proporciona un resumen visual de las relaciones entre variables en correl_data. Los valores de correlación van de -1 a 1, donde los valores más próximos a 1 indican una fuerte correlación positiva, los valores más próximos a -1 indican una fuerte correlación negativa, y los valores en torno a 0 sugieren que no hay correlación. Es evidente que no existe una correlación fuerte por pares entre las variables, ya que ninguno de los valores de correlación supera siquiera el 0,6. 

El siguiente paso es calcular los valores VIF de las variables predictoras. El código siguiente calcula los valores de cada variable predictora del conjunto de datos para comprobar si hay multicolinealidad. 

En primer lugar, define X eliminando la columna objetivo Performance y añadiendo una intercepción. A continuación, crea un DataFrame, datacamp_vif_data, para almacenar los nombres de los predictores y sus valores VIF. Mediante un bucle, calcula a continuación el VIF de cada predictor con lafunción variance_inflation_factor() , donde los VIF más altos indican la presencia de multicolinealidad .

# Define the predictor variables
X = datacamp_retail_data.drop(columns=['Performance'])

# Add a constant to the model (intercept)
X = add_constant(X)

# Calculate VIF for each feature
datacamp_vif_data = pd.DataFrame()
datacamp_vif_data['Feature'] = X.columns
datacamp_vif_data['VIF'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(datacamp_vif_data)

Salida:

Salida que muestra los valores VIF. Imagen del autor

Esta salida muestra el valor VIF de cada variable predictora, que indica los niveles de multicolinealidad en el conjunto de datos. La fila const representa el término de intercepción, con un VIF cercano a 1, lo que significa que no tiene multicolinealidad. Entre las variables predictoras, Product_range tiene el VIF más alto (5,94), lo que sugiere que necesita medidas correctoras. Todos los demás predictores tienen valores VIF inferiores a 3, lo que indica una baja multicolinealidad. 

Enfoque manual del cálculo del VIF

El otro enfoque consiste en calcular los valores por separado haciendo una regresión de cada variable independiente frente a las demás variables predictoras.  

Funciona así: para cada rasgo de retail_data, establece ese rasgo como variable dependiente (y) y el resto de rasgos como variables independientes (X). A continuación, se ajusta un modelo de regresión lineal para predecir y mediante X, y el valor R-cuadrado del modelo se utiliza para calcular el VIF mediante la fórmula que comentamos en el apartado inicial.

Posteriormente, cada característica y sus correspondientes valores VIF se almacenan en un diccionario (vif_manual), que luego se convierte en un DataFrame (vif_manual_df) para su visualización. 

datacamp_retail_data = retail_data.drop(columns=['Performance'])

# Manual VIF Calculation
vif_manual = {}

for feature in retail_data.columns:
    # Define the target variable (current feature) and predictors (all other features)
    y = datacamp_retail_data[feature]
    X = datacamp_retail_data.drop(columns=[feature])

    # Fit the linear regression model
    model = LinearRegression().fit(X, y)

    # Calculate R-squared
    r_squared = model.score(X, y)

    # Calculate VIF
    vif = 1 / (1 - r_squared)
    vif_manual[feature] = vif

# Convert the dictionary to a DataFrame for better display
vif_manual_df = pd.DataFrame(list(vif_manual.items()), columns=['Feature', 'VIF'])
print(vif_manual_df)

 Salida:

Salida que muestra los valores VIF. Imagen del autor

El resultado muestra cada característica junto con su valor VIF, lo que ayuda a identificar posibles problemas de multicolinealidad. Puedes ver que el resultado es obviamente el mismo que obtuvimos anteriormente; y también lo será su interpretación, que es que la variable Product_range presenta multicolinealidad.

Factor de inflación de la varianza en R

En esta sección, repetiremos el ejercicio del factor de inflación de la varianza anterior en la sección de Python, especialmente para los desarrolladores que trabajan con el lenguaje de programación R. Comenzamos cargando el conjunto de datos y las bibliotecas necesarias.

library(tidyverse)
library(car)
library(corrplot)

data <- read.csv('vif_data.csv')
str(data)

Salida:

El siguiente paso es calcular la matriz de correlaciones por pares, y visualizarla con el mapa de calor. Las funciones cor() y corrplot nos ayudan a realizar esta tarea.

# Remove the target column
predictors_data <- data[, !(names(data) %in% "Performance")]

# Calculate the correlation matrix
correlation_matrix <- cor(predictors_data)

# Plot the correlation heatmap
# Load necessary libraries
library(ggplot2)
library(reshape2)
melted_corr_matrix <- melt(correlation_matrix)

# Plot the heatmap with ggplot2
ggplot(data = melted_corr_matrix, aes(x = Var1, y = Var2, fill = value)) +
  geom_tile(color = "white") +
  scale_fill_gradient2(low = "blue", high = "red", mid = "white", 
                       midpoint = 0, limit = c(-1, 1), space = "Lab", 
                       name="Correlation") +
  theme_minimal() + # Minimal theme for a clean look
  theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1)) +
  labs(x = "", y = "") + # Remove axis labels
  geom_text(aes(Var1, Var2, label = round(value, 2)), color = "black", size = 4) +
  theme(axis.text=element_text(size=15))

Salida:

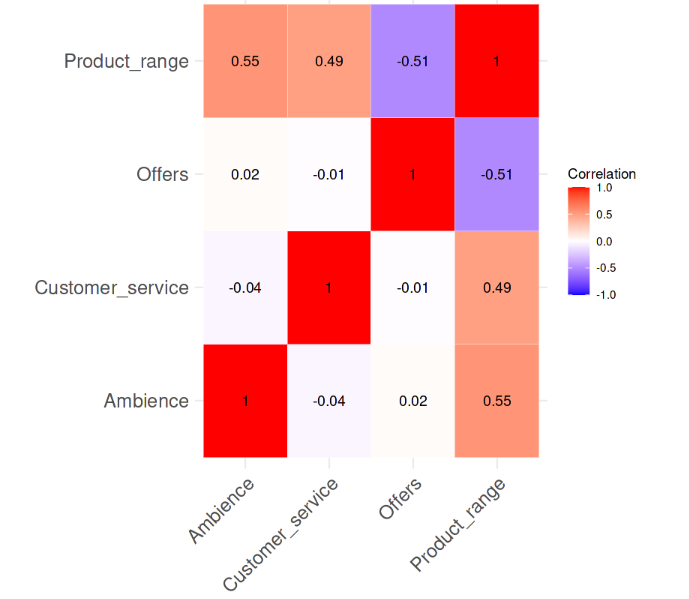
Correlación entre las variables. Imagen del autor

En el mapa de correlación se observa que no existe una correlación fuerte entre las variables, ya que ninguno de los valores de correlación es superior a 0,6. Ahora, calcularemos los valores VIF y veremos si hay algo alarmante. La siguiente línea de código realiza esa tarea. 

# Fit a regression model
model <- lm(Performance ~ Ambience + Customer_service + Offers + Product_range, data = data)

# Calculate VIF
vif(model)

Salida:

A partir del resultado, podemos ver que entre las variables predictoras, sólo la variable Product_range tiene un valor VIF superior a 5, lo que sugiere una elevada multicolinealidad que requiere medidas correctoras. 

Enfoque manual del cálculo del VIF

La otra forma de calcular el VIF sería calcular los valores VIF de cada variable por separado haciendo una regresión de cada variable independiente frente a las demás variables predictoras.  

Esto se realiza en el código siguiente, que utiliza la función sapply()en cada predictor, donde cada predictor se establece como variable dependiente en un modelo de regresión lineal con los demás predictores como variables independientes. 

El valor R-cuadrado de cada modelo se utiliza después para calcular los valores VIF con su fórmula. Por último, el resultado, vif_values, muestra el VIF de cada predictor, lo que ayuda a identificar problemas de multicolinealidad.

# VIF calculation for each predictor manually
predictors <- c("Ambience", "Customer_service", "Offers", "Product_range")

vif_values <- sapply(predictors, function(pred) {
    formula <- as.formula(paste(pred, "~ ."))
    model <- lm(formula, data = data[, predictors])
    1 / (1 - summary(model)$r.squared)
})

print(vif_values)

Salida:

Obtenemos el mismo resultado y es evidente que la variable Product_range con un valor VIF alto, superior a 5, necesita intervención. 

VIF frente a Matriz de correlación y otros métodos

A modo de recapitulación, he aquí los métodos más conocidos para detectar la multicolinealidad:

• Valores VIF elevados: Un valor VIF elevado es un claro indicador de multicolinealidad. Cuando estos valores superan determinados umbrales, indican que un predictor está fuertemente relacionado con otros predictores, lo que puede afectar a la estabilidad, fiabilidad y rendimiento del modelo.
• Matrices de correlación: Examinando una matriz de correlaciones, puedes ver las correlaciones por pares entre predictores. Las correlaciones por pares elevadas sugieren multicolinealidad entre esos predictores específicos. Sin embargo, este método sólo detecta las relaciones lineales directas entre dos variables y puede pasar por alto la multicolinealidad que implica interacciones más complejas entre varias variables.
• Cambios de coeficiente: Si los coeficientes de los predictores cambian significativamente cuando añades o eliminas otras variables del modelo, puede ser un signo de multicolinealidad. Tales fluctuaciones indican que ciertos predictores pueden estar compartiendo información común, lo que hace más difícil identificar el impacto único de cada variable en el resultado.

Entre todos estos métodos, el VIF es especialmente útil porque puede detectar la multicolinealidad incluso cuando las correlaciones entre pares son bajas, como vimos en nuestro propio ejemplo. Esto hace que VIF sea una herramienta más completa.

Ideas adicionales sobre cómo abordar los valores VIF elevados

Si los valores VIF indican una alta multicolinealidad, y no necesariamente quieres eliminar la variable, existen otras estrategias más avanzadas para mitigar la multicolinealidad:

1. Selección de características: Elimina uno de los predictores altamente correlacionados y vuelve a calcular el VIF para ver si ayuda a simplificar el modelo y mejorar la estabilidad.
2. Análisis de Componentes Principales (ACP): Utiliza el ACP para combinar tus predictores en un conjunto más pequeño de componentes no correlacionados. Esto transforma las variables originales en otras nuevas, independientes y no correlacionadas, que captan la mayor parte de la variación de los datos, ayudando a abordar la multicolinealidad sin perder información valiosa.
3. Técnicas de regularización: Aplica la regresión ridge o lasso, que añaden términos de penalización al modelo. Estas técnicas ayudan a reducir la multicolinealidad reduciendo la influencia de las variables correlacionadas, lo que hace que el modelo sea más estable y fiable.

Conclusión

Saber utilizar el VIF es clave para identificar y corregir la multicolinealidad, lo que mejora la precisión y claridad de los modelos de regresión. Comprobar regularmente los valores VIF y aplicar medidas correctoras cuando sea necesario ayuda a los profesionales y analistas de datos a construir modelos en los que puedan confiar. Este enfoque garantiza que el efecto de cada predictor sea claro, lo que facilita extraer conclusiones fiables del modelo y tomar mejores decisiones basadas en los resultados. Accede a a nuestro itinerario profesional de Científico de Aprendizaje Automático en Python para comprender realmente cómo construir modelos y utilizarlos. Además, la finalización del programa queda muy bien en un currículum.

Además, para seguir aprendiendo, considera la posibilidad de explorar los siguientes recursos del blog de DataCamp y las secciones de tutoriales:

• Fundamentos de Regresión Lineal en Python: Aprende qué formula un problema de regresión y cómo funciona un algoritmo de regresión lineal en Python.
• Cómo hacer regresión lineal en R: Aprende regresión lineal, un modelo estadístico que analiza la relación entre variables utilizando R.
• Descomposición QR en el Aprendizaje Automático: Guía detallada: Conoce la descomposición QR, la técnica de factorización de matrices que descompone la matriz A en el producto de una matriz ortogonal Q y una matriz triangular superior R.
• Tutorial de Lasso y Regresión Ridge en Python: Conoce las técnicas de regresión del lazo y la cresta. Compara y analiza los métodos en detalle.