Facteur d'inflation de la variance (VIF) : Traitement de la multicolinéarité dans l'analyse de régression

Qu'est-ce que le facteur d'inflation de la variance (VIF) ?

Développé par le statisticien Cuthbert Daniel, le VIF est un outil de diagnostic largement utilisé dans l'analyse de régression pour détecter la multicolinéarité, connue pour affecter la stabilité et l'interprétabilité des coefficients de régression. Plus techniquement, le VIF quantifie la variance d'un coefficient de régression en raison des corrélations entre les variables prédictives.

Tout ceci est important car ces corrélations rendent difficile l'isolement de l'effet unique de chaque prédicteur sur la variable cible, ce qui conduit à des estimations de modèle moins fiables. Il convient également de préciser que, pour que l'information soit vraiment pertinente, la VIF est toujours calculée pour chaque prédicteur d'un modèle.

La formule du facteur d'inflation de la variance

Le VIF pour un prédicteur X est calculé comme suit :

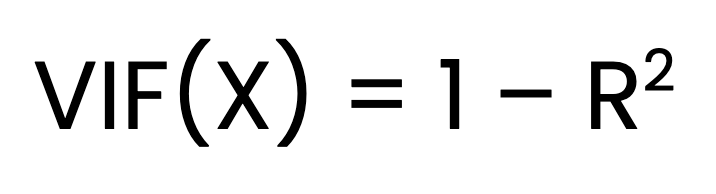
Où ?

• ^R2 est le coefficient de détermination obtenu lorsque X​ est régressé sur tous les autres prédicteurs.

Calcul étape par étape

La recherche de l'IVF se fait en trois étapes. La première étape consiste à ajuster un modèle de régression linéaire distinct pour chaque prédicteur par rapport à tous les autres prédicteurs. La deuxième étape consiste à obtenir la valeur^R2 pour chaque modèle. La dernière étape consiste à calculer le VIF à l'aide de la formule ci-dessus.

Interprétation des valeurs VIF

Voici comment interpréter les valeurs VIF pour comprendre le niveau de multicolinéarité :

• VIF = 1: Cela indique qu'il n'y a pas de multicolinéarité. Le prédicteur n'est pas corrélé avec d'autres prédicteurs, il ne gonfle donc pas l'erreur standard et n'affecte pas la stabilité du modèle.
• VIF entre 1 et 5: Cela suggère une multicolinéarité modérée. Il existe une certaine corrélation avec d'autres facteurs prédictifs, mais elle n'est généralement pas très marquée. Toutefois, il convient de surveiller ces prédicteurs pour voir si la multicolinéarité devient un problème, en particulier si d'autres valeurs VIF sont élevées.
• VIF > 5: Il existe une forte multicolinéarité. L'erreur type du prédicteur peut être notablement gonflée, ce qui peut rendre son coefficient moins fiable. Envisagez de prendre des mesures pour réduire la multicolinéarité, par exemple en supprimant ou en combinant les variables prédictives corrélées.
• VIF > 10: Ceci est le signe d'une grave multicolinéarité. L'erreur type du prédicteur est fortement gonflée et l'estimation de son coefficient est probablement instable. Des mesures correctives, telles que la suppression du prédicteur ou l'utilisation de techniques de régularisation, sont généralement nécessaires.

Par exemple, si la VIF d'un prédicteur est de 10, cela signifie que la variance du coefficient de ce prédicteur est 10 fois supérieure à ce qu'elle serait s'il n'y avait pas de multicolinéarité. 

Comment le VIF explique la multicolinéarité dans la régression

La multicolinéarité entraîne une augmentation des erreurs types, ce qui rend plus difficile l'évaluation de l'importance des prédicteurs individuels. Cela est dû au fait que les variables colinéaires contiennent des informations similaires, ce qui rend difficile la séparation de leurs effets individuels spécifiques sur la variable de résultat. 

Bien que la multicollinéarité ne nuise pas nécessairement à la capacité de prédiction du modèle, elle réduit la fiabilité et la clarté des coefficients. Ceci est particulièrement problématique lorsque nous voulons comprendre l'impact individuel de chaque prédicteur.

Le facteur d'inflation de la variance (VIF) est une mesure diagnostique précise permettant d'identifier la multicolinéarité. Contrairement aux observations générales sur la corrélation, la VIF isole l'effet combiné de tous les prédicteurs sur chaque variable, en mettant en évidence les interactions qui pourraient ne pas être évidentes à partir des corrélations par paire.

Facteur d'inflation de la variance en Python et R

Pour que cela soit réalisable, nous allons voir un exemple à la fois en Python et en R en utilisant un ensemble de données unique. Nous calculerons le VIF à l'aide de logiciels automatisés et nous utiliserons également la formule du VIF pour développer notre intuition. Afin d'avoir une bonne pratique, j'ai délibérément créé un ensemble de données où nous découvrirons une valeur VIF élevée pour l'une de nos variables même s'il n'y a pas de corrélation par paire très élevée entre deux variables - je pense donc qu'il s'agit d'un exemple convaincant. Commençons par un aperçu de l'ensemble de données que nous allons utiliser.

Aperçu de l'ensemble des données :

Cet ensemble de données fictives représente les résultats d'une étude menée dans 1 000 magasins d'un géant de la distribution. Les clients de chaque magasin ont été invités à évaluer divers aspects de leur expérience d'achat sur une échelle de -5 à +5, où -5 indique une expérience très négative et +5 une expérience très positive. La moyenne des évaluations des clients de chaque magasin a été calculée sur la base de quatre paramètres clés :

• Ambience: Perception par le client de l'environnement du magasin, comme la propreté, l'agencement, l'éclairage et l'atmosphère générale. 

• Customer_service: Évaluation du service fourni par le personnel du magasin, y compris la serviabilité, l'amabilité et la réactivité aux besoins du client.

• Offers: Classement des offres promotionnelles, des remises et des bons plans du magasin proposés aux clients.

• Product_range: Évaluation de la variété et de la qualité des produits disponibles dans le magasin.

La variable cible, Performance, mesure la performance globale de chaque magasin. Cependant, cela n'est pas pertinent du point de vue de l'IVF. Vous pouvez télécharger l'ensemble des données ici. 

Facteur d'inflation de la variance en Python

Nous commencerons par calculer les valeurs VIF à l'aide des paquets Python. La première étape consiste à charger le jeu de données et les bibliothèques nécessaires. 

from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.tools.tools import add_constant

datacamp_retail_data = pd.read_csv(' vif_data.csv')
datacamp_retail_data.head()

Le code ci-dessus charge les données et affiche les cinq premiers enregistrements. 

L'étape suivante consiste à exécuter une matrice de corrélation pour vérifier l'existence d'une corrélation par paire.

Le code ci-dessous sélectionne quatre colonnes et les stocke dans un nouveau DataFrame appelé correl_data . Il calcule ensuite la matrice de corrélation par paire à l'aide de la fonction .corr(). Le résultat est stocké dans l'objet corr_matrix, qui est un tableau indiquant les coefficients de corrélation entre chaque paire de colonnes sélectionnées. 

La matrice est ensuite visualisée à l'aide de la fonction heatmap() de Seaborn, qui affiche chaque coefficient de corrélation sous la forme d'une cellule codée en couleur, le bleu représentant les corrélations négatives et le rouge les corrélations positives, sur la base de la carte des couleurs de coolwarm. 

correl_data = datacamp_retail_data[['Ambience', 'Customer_service', 'Offers', 'Product_range']]

# Compute the pairwise correlation matrix
corr_matrix = correl_data.corr()

# Visualize the correlation matrix
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('Pairwise Correlation Matrix')
plt.show()

Sortie :

  Corrélation entre les variables. Image par l'auteur

Le graphique fournit un résumé visuel des relations entre les variables dans correl_data. Les valeurs de corrélation sont comprises entre -1 et 1, les valeurs proches de 1 indiquant une forte corrélation positive, les valeurs proches de -1 indiquant une forte corrélation négative et les valeurs proches de 0 indiquant l'absence de corrélation. Il est évident qu'il n'y a pas de forte corrélation par paire entre les variables, aucune des valeurs de corrélation n'étant supérieure à 0,6. 

L'étape suivante consiste à calculer les valeurs VIF pour les variables prédictives. Le code ci-dessous calcule les valeurs de chaque variable prédictive de l'ensemble de données afin de vérifier la multicolinéarité. 

Tout d'abord, il définit X en supprimant la colonne cible Performance et en ajoutant une ordonnée à l'origine. Il crée ensuite un DataFrame, datacamp_vif_data, pour stocker les noms des variables prédicteurs et leurs valeurs VIF. À l'aide d'une boucle, il calcule ensuite le VIF pour chaque prédicteur à l'aide de lafonction variance_inflation_factor() , où des VIF élevés indiquent la présence de multicolinéarité .

# Define the predictor variables
X = datacamp_retail_data.drop(columns=['Performance'])

# Add a constant to the model (intercept)
X = add_constant(X)

# Calculate VIF for each feature
datacamp_vif_data = pd.DataFrame()
datacamp_vif_data['Feature'] = X.columns
datacamp_vif_data['VIF'] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(datacamp_vif_data)

Sortie :

Sortie montrant les valeurs VIF. Image par l'auteur

Cette sortie montre la valeur VIF pour chaque variable prédictive, indiquant les niveaux de multicolinéarité dans l'ensemble de données. La ligne const représente le terme d'interception, avec un VIF proche de 1, ce qui signifie qu'il n'y a pas de multicolinéarité. Parmi les variables prédictives, Product_range présente le VIF le plus élevé (5,94), ce qui suggère qu'elle nécessite des mesures correctives. Tous les autres prédicteurs ont des valeurs VIF inférieures à 3, ce qui indique une faible multicolinéarité. 

Approche manuelle du calcul du VIF

L'autre approche consiste à calculer les valeurs séparément en régressant chaque variable indépendante par rapport aux autres variables prédictives.  

Le fonctionnement est le suivant : pour chaque caractéristique de retail_data, la variable dépendante (y) est définie et les autres caractéristiques sont des variables indépendantes (X). Un modèle de régression linéaire est ensuite ajusté pour prédire y à partir de X, et la valeur R au carré du modèle est utilisée pour calculer le VIF à l'aide de la formule que nous avons présentée dans la section initiale.

Ensuite, chaque caractéristique et ses valeurs VIF correspondantes sont stockées dans un dictionnaire (vif_manual), qui est ensuite converti en DataFrame (vif_manual_df) pour l'affichage. 

datacamp_retail_data = retail_data.drop(columns=['Performance'])

# Manual VIF Calculation
vif_manual = {}

for feature in retail_data.columns:
    # Define the target variable (current feature) and predictors (all other features)
    y = datacamp_retail_data[feature]
    X = datacamp_retail_data.drop(columns=[feature])

    # Fit the linear regression model
    model = LinearRegression().fit(X, y)

    # Calculate R-squared
    r_squared = model.score(X, y)

    # Calculate VIF
    vif = 1 / (1 - r_squared)
    vif_manual[feature] = vif

# Convert the dictionary to a DataFrame for better display
vif_manual_df = pd.DataFrame(list(vif_manual.items()), columns=['Feature', 'VIF'])
print(vif_manual_df)

 Sortie :

Sortie montrant les valeurs VIF. Image par l'auteur

Le résultat montre chaque caractéristique avec sa valeur VIF, ce qui permet d'identifier les problèmes potentiels de multicolinéarité. Vous pouvez voir que le résultat est évidemment le même que celui que nous avons obtenu ci-dessus ; il en va de même pour son interprétation, à savoir que la variable Product_range présente une multicolinéarité.

Facteur d'inflation de la variance dans R

Dans cette section, nous allons répéter l'exercice du facteur d'inflation de la variance ci-dessus dans la section Python, en particulier pour les développeurs qui travaillent avec le langage de programmation R. Nous commençons par charger le jeu de données et les bibliothèques nécessaires.

library(tidyverse)
library(car)
library(corrplot)

data <- read.csv('vif_data.csv')
str(data)

Sortie :

L'étape suivante consiste à calculer la matrice de corrélation par paire et à la visualiser à l'aide de la carte thermique. Les fonctions cor() et corrplot nous aident à accomplir cette tâche.

# Remove the target column
predictors_data <- data[, !(names(data) %in% "Performance")]

# Calculate the correlation matrix
correlation_matrix <- cor(predictors_data)

# Plot the correlation heatmap
# Load necessary libraries
library(ggplot2)
library(reshape2)
melted_corr_matrix <- melt(correlation_matrix)

# Plot the heatmap with ggplot2
ggplot(data = melted_corr_matrix, aes(x = Var1, y = Var2, fill = value)) +
  geom_tile(color = "white") +
  scale_fill_gradient2(low = "blue", high = "red", mid = "white", 
                       midpoint = 0, limit = c(-1, 1), space = "Lab", 
                       name="Correlation") +
  theme_minimal() + # Minimal theme for a clean look
  theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1)) +
  labs(x = "", y = "") + # Remove axis labels
  geom_text(aes(Var1, Var2, label = round(value, 2)), color = "black", size = 4) +
  theme(axis.text=element_text(size=15))

Sortie :

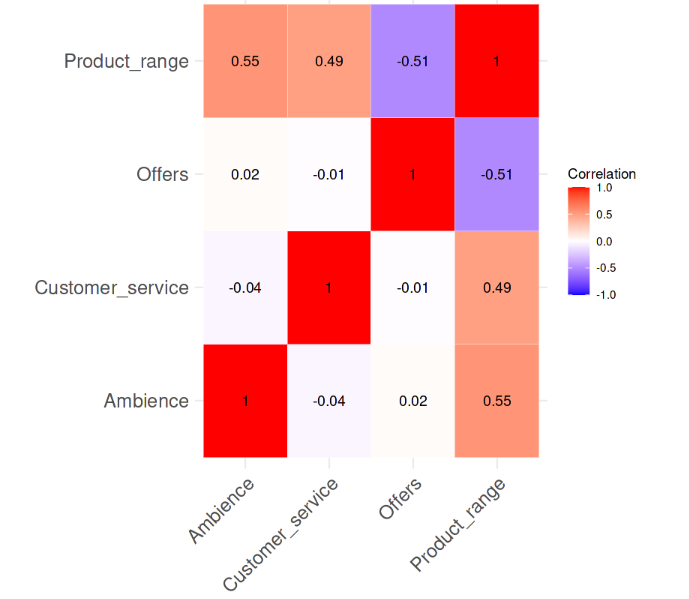
Corrélation entre les variables. Image par l'auteur

La carte thermique des corrélations montre clairement qu'il n'y a pas de forte corrélation entre les variables, aucune valeur de corrélation n'étant supérieure à 0,6. Nous allons maintenant calculer les valeurs VIF et voir s'il y a quelque chose d'alarmant. La ligne de code suivante s'acquitte de cette tâche. 

# Fit a regression model
model <- lm(Performance ~ Ambience + Customer_service + Offers + Product_range, data = data)

# Calculate VIF
vif(model)

Sortie :

Le résultat montre que parmi les variables prédictives, seule la variable Product_range a une valeur VIF supérieure à 5, ce qui suggère une forte multicolinéarité nécessitant des mesures correctives. 

Approche manuelle du calcul de l'IVF

L'autre approche du calcul du VIF consisterait à calculer les valeurs du VIF pour chaque variable séparément en régressant chaque variable indépendante par rapport aux autres variables prédictives.  

Cette opération est réalisée dans le code ci-dessous, qui utilise la fonction sapply()pour chaque prédicteur, où chaque prédicteur est défini comme la variable dépendante dans un modèle de régression linéaire avec les autres prédicteurs comme variables indépendantes. 

La valeur R au carré de chaque modèle est ensuite utilisée pour calculer les valeurs VIF à l'aide de sa formule. Enfin, le résultat, vif_values, affiche le VIF pour chaque prédicteur, ce qui permet d'identifier les problèmes de multicolinéarité.

# VIF calculation for each predictor manually
predictors <- c("Ambience", "Customer_service", "Offers", "Product_range")

vif_values <- sapply(predictors, function(pred) {
    formula <- as.formula(paste(pred, "~ ."))
    model <- lm(formula, data = data[, predictors])
    1 / (1 - summary(model)$r.squared)
})

print(vif_values)

Sortie :

Nous obtenons le même résultat et il est évident que la variable Product_range dont la valeur VIF est supérieure à 5 doit faire l'objet d'une intervention. 

VIF vs. Matrice de corrélation et autres méthodes

Pour rappel, voici les méthodes les plus courantes pour détecter la multicollinéarité :

• Valeurs élevées de l'IVF: Une valeur VIF élevée est un indicateur clair de multicolinéarité. Lorsque ces valeurs dépassent certains seuils, elles indiquent qu'un prédicteur est fortement lié à d'autres prédicteurs, ce qui peut affecter la stabilité, la fiabilité et la performance du modèle.
• Matrices de corrélation: En examinant une matrice de corrélation, vous pouvez voir les corrélations par paire entre les prédicteurs. Des corrélations élevées par paire suggèrent une multicolinéarité entre ces prédicteurs spécifiques. Cependant, cette méthode ne détecte que les relations linéaires directes entre deux variables et peut manquer la multicolinéarité impliquant des interactions plus complexes entre plusieurs variables.
• Changements de coefficients: Si les coefficients des variables prédictives changent de manière significative lorsque vous ajoutez ou supprimez d'autres variables du modèle, cela peut être un signe de multicolinéarité. De telles fluctuations indiquent que certains prédicteurs peuvent partager des informations communes, ce qui rend plus difficile l'identification de l'impact unique de chaque variable sur le résultat.

Parmi toutes ces méthodes, le VIF est particulièrement utile car il permet de détecter la multicolinéarité même lorsque les corrélations par paire sont faibles, comme nous l'avons vu dans notre propre exemple. Le VIF est donc un outil plus complet.

Idées supplémentaires sur la manière de traiter les valeurs élevées de l'IVF

Si les valeurs VIF indiquent une forte multicollinéarité et que vous ne souhaitez pas nécessairement supprimer la variable, il existe d'autres stratégies plus avancées pour atténuer la multicollinéarité :

1. Sélection des caractéristiques: Supprimez l'un des prédicteurs fortement corrélés et recalculez le VIF pour voir s'il permet de simplifier le modèle et d'en améliorer la stabilité.
2. Analyse en composantes principales (ACP): Utilisez l'ACP pour combiner vos prédicteurs en un ensemble plus restreint de composantes non corrélées. Les variables initiales sont ainsi transformées en de nouvelles variables indépendantes et non corrélées qui capturent la plupart des variations des données, ce qui permet de remédier à la multicolinéarité sans perdre d'informations précieuses.
3. Techniques de régularisation: Appliquez la régression ridge ou lasso, qui ajoute des termes de pénalité au modèle. Ces techniques permettent de réduire la multicolinéarité en diminuant l'influence des variables corrélées, ce qui rend le modèle plus stable et plus fiable.

Conclusion

Savoir utiliser la VIF est essentiel pour identifier et corriger la multicolinéarité, ce qui améliore la précision et la clarté des modèles de régression. En vérifiant régulièrement les valeurs VIF et en appliquant des mesures correctives si nécessaire, les professionnels des données et les analystes construisent des modèles auxquels ils peuvent se fier. Cette approche garantit que l'effet de chaque prédicteur est clair, ce qui permet de tirer des conclusions fiables du modèle et de prendre de meilleures décisions sur la base des résultats. Prenez notre cursus de carrière Machine Learning Scientist in Python pour vraiment comprendre comment construire des modèles et les utiliser. De plus, l'achèvement du programme fait bonne figure sur un CV.

De plus, pour un apprentissage plus approfondi, pensez à explorer les ressources suivantes issues des sections blog et tutoriels de DataCamp :

• L'essentiel de la régression linéaire en Python : Découvrez ce qui formule un problème de régression et comment fonctionne un algorithme de régression linéaire en Python.
• Comment effectuer une régression linéaire dans R : Apprenez la régression linéaire, un modèle statistique qui analyse la relation entre les variables à l'aide de R.
• Décomposition QR dans l'apprentissage automatique : Un guide détaillé: Découvrez la décomposition QR, la technique de factorisation matricielle qui décompose la matrice A en un produit d'une matrice orthogonale Q et d'une matrice triangulaire supérieure R.
• Tutoriel sur la régression Lasso et Ridge en Python: Découvrez les techniques de régression lasso et ridge. Comparez et analysez les méthodes en détail.