Explicación de las redes neuronales feed-forward: Un tutorial completo

Al analizar los algoritmos de machine learning, hay muy pocos conceptos tan fundamentales como la red neuronal feed-forward (FFNN). Si alguna vez has creado tu primera red neuronal, es muy probable que fuera una red feed-forward. Se pueden ver en casi todas partes, desde problemas de clasificación simples hasta capas de potenciación en arquitecturas profundas.

En primer lugar, permíteme mostrarte dónde encajan las redes neuronales feed-forward en el panorama general:

En este tutorial, explicaré qué es realmente una red neuronal feed-forward, cómo ha evolucionado y por qué sigue siendo relevante hoy en día, además de explorar ejemplos del mundo real.

¿Qué es una red neuronal feed-forward?

Intuitivamente, la mejor manera de describir una arquitectura de red de este tipo es «los datos solo fluyen hacia adelante, sin bucles»

En esencia, una FFNN procesa los datos de tal manera que fluyen en una sola dirección, desde la entrada hasta la salida. No hay bucles, ni recursividad, ni ciclos (exceptola retropropagación e , que veremos en breve).

Cuando empecé a aprender sobre esto, la imagen mental que más me ayudó fue la de una cinta transportadora de fábrica. 

¿Por qué? 

Porque cada paso del proceso (o cada capa de la red) realiza una acción sencilla sobre la entrada antes de pasarla a la siguiente.

Así es como funciona:

1. Las entradas se introducen en la primera capa (la capa de entrada).
2. Se transforman mediante pesos y sesgos y se pasan a través de una función de activación.
3. Esto continúa a través de una o más capas ocultas.
4. Por último, la capa de salida realiza una predicción.

Antes de mostrarte cómo es una arquitectura de red de este tipo, quiero aclarar un error común:

«Las redes neuronales feed-forward son lo mismo que las MLP».

Para aclarar este concepto erróneo, debemos explorar los inicios de la historia del aprendizaje profundo. 

Historia temprana del aprendizaje profundo

Perceptrón: Comenzamos con elperceptrón e , inventado en la década de 1950 por Frank Rosenblatt. Era un clasificador binario de una sola capa y, aunque no podía resolverlo todo (como los problemas XOR), sentó las bases para las redes neuronales.

En palabras sencillas, un perceptrón funcionaba así:

1. Entradas: Cada entrada (como x_1, x_2, etc.) tiene un peso asociado (w_1, w_2, etc.).
2. Suma ponderada: Las entradas se multiplican por sus pesos y se suman, junto con un término de sesgo: z = w1*x1 + w2*x2+ ... + b.
3. Activación: El resultado se pasa por una función escalonada (una activación). Si el valor está por encima de un umbral, el perceptrón genera un 1; de lo contrario, genera un 0.

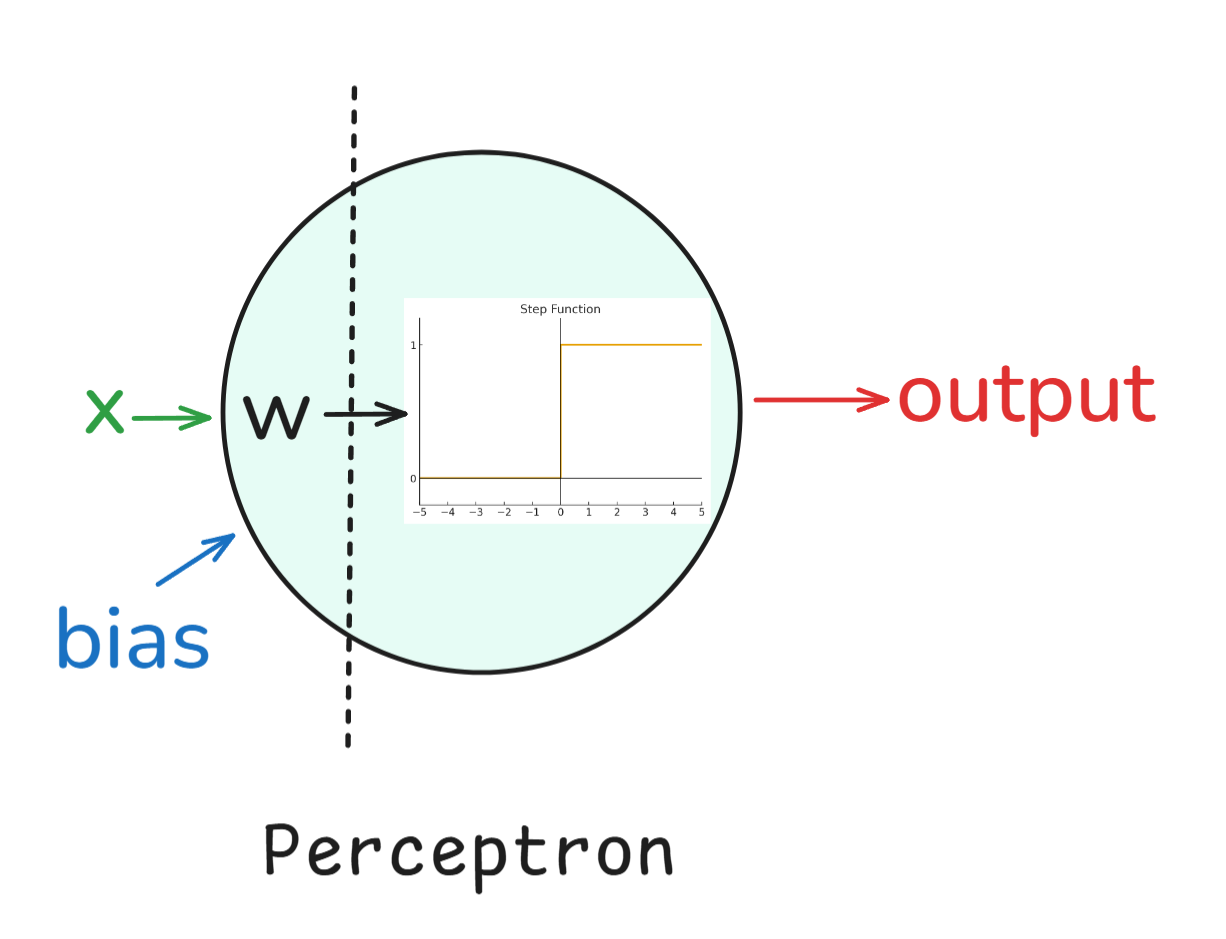
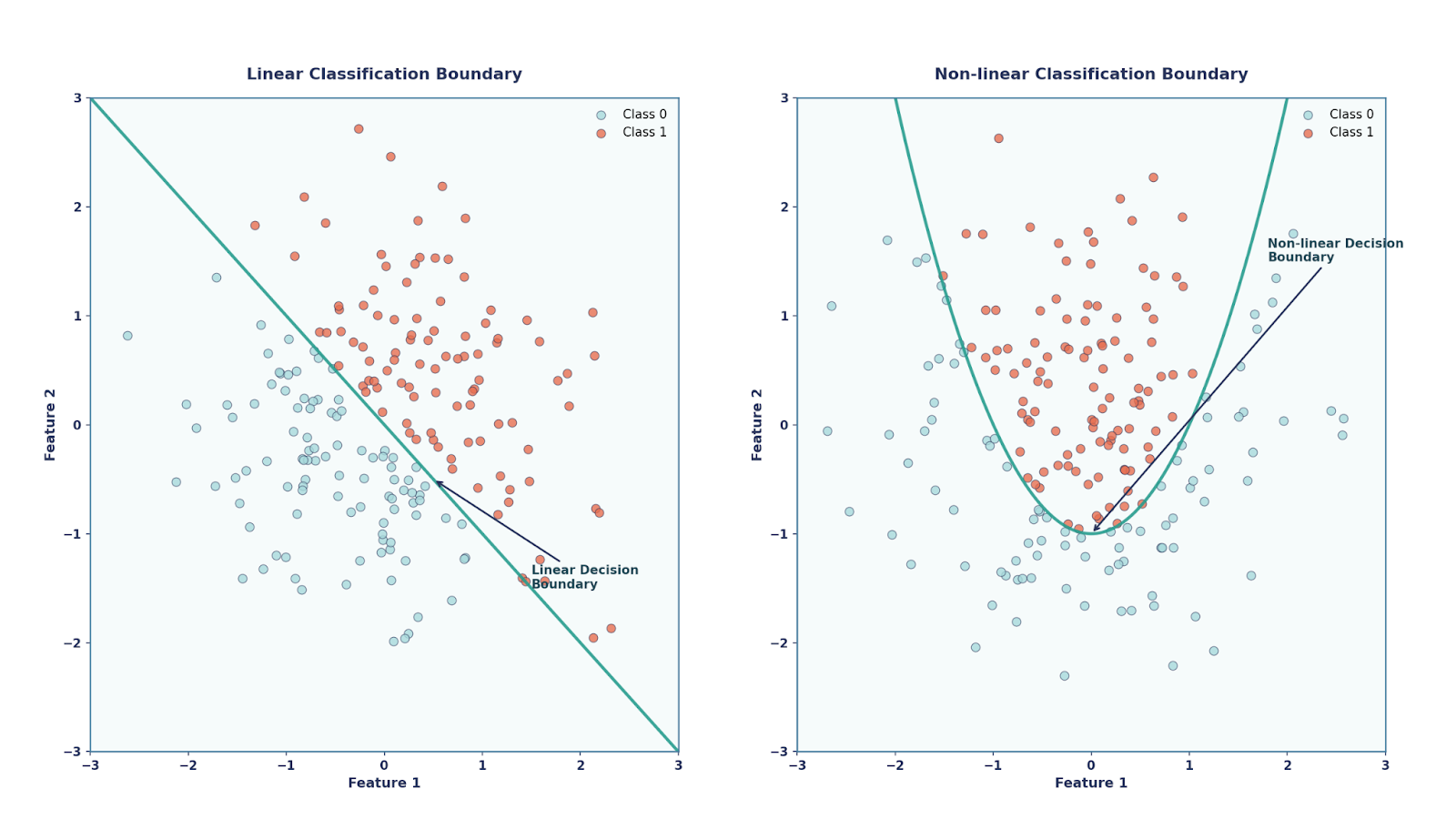
Básicamente, el perceptrón es un clasificador lineal, lo que significa que solo puede trazar límites de decisión en línea recta (o hiperplanos). Por un lado, el perceptrón tenía sus ventajas, como ser muy sencillo y elegante (ya que se inspiraba en la biología), además de ser computacionalmente económico. Por otro lado, sin embargo, no podía resolver problemas que no fueran linealmente separables, como el problema XOR. 

Perceptrones multicapa (MLP): Unas décadas más tarde, en la década de 1980, los investigadores descubrieron que si se apilaban varios perceptrones y se añadían funciones de activación no lineales, se podían resolver problemas más complejos. Esta estructura se conoció como el perceptrón multicapa.

Así es como funcionaba: 

1. Capa de entrada: Se tomaron las características sin procesar del conjunto de datos.
2. Capas ocultas: Una o más capas de perceptrones que aplican transformaciones. Cada neuronarealizab o z = w*x + b y lo pasabais a través de una función de activación no lineal, como sigmoide, tanh, etc.
3. Capa de salida: La capa final produjo la predicción final (por ejemplo, probabilidades de clase, valores de regresión).

La incorporación de estas activaciones no lineales fue crucial. Sin ellos, las capas apiladas se colapsarían en una única transformación lineal. Con ellos, las MLP podrían representar funciones no lineales muy complejas.

Esto condujo a uno de los resultados más famosos de la teoría de las redes neuronales: el Teorema de Aproximación Universal.

Este teorema establece que una red neuronal con una sola capa oculta, siempre que tenga una función de activación no lineal y suficientes neuronas, puede aproximarse a cualquier función continua en un dominio acotado. 

La era del aprendizaje profundo: Al avanzar hacia la década de 2010, entramos en la era del aprendizaje profundo. Con las GPU y el big data, las FFNN evolucionaron hacia arquitecturas más profundas y potentes, sentando las bases para las CNN, las RNN y los transformadores, que es donde nos encontramos esencialmente en la actualidad.

Volviendo ahora al concepto erróneo original, ahora sabemos que:

• Red neuronal feed-forward (FFNN). Categoría general de cualquier red neuronal en la que los datos fluyen en una sola dirección (entrada → oculta → salida), sin bucles.
• Perceptrón multicapa (MLP). Untipo de FFN e e que tiene específicamente al menos una capa oculta de perceptrones (neuronas con pesos, sesgos y activación).

En otras palabras, todas las MLP son FFNN, pero no todas las FFNN son MLP. Es muy importante recordar este punto. Otro error común es el relativo al perceptrón de una sola capa (es decir, solo de entrada a salida).

Un perceptrón de una sola capa es una FFNN, ¡pero no una MLP! Solo cuando añadimos capas ocultas, se convierte en una MLP.

Esta distinción es importante, ya que las MLP son capaces de aproximar funciones universales (con suficientes unidades ocultas y funciones de activación no lineales), mientras que los perceptrones simples de una sola capa están limitados en lo que pueden representar.

Arquitectura de una red neuronal feed-forward

En la sección anterior, hemos aprendido mucho sobre las FFNN, pero, en pocas palabras, pueden considerarse como un a una pila de transformaciones simples. Hay muchos componentes diferentes que crean una FFNN, así que vamos a explorarlos con más detalle, en particular la estructura MLP. 

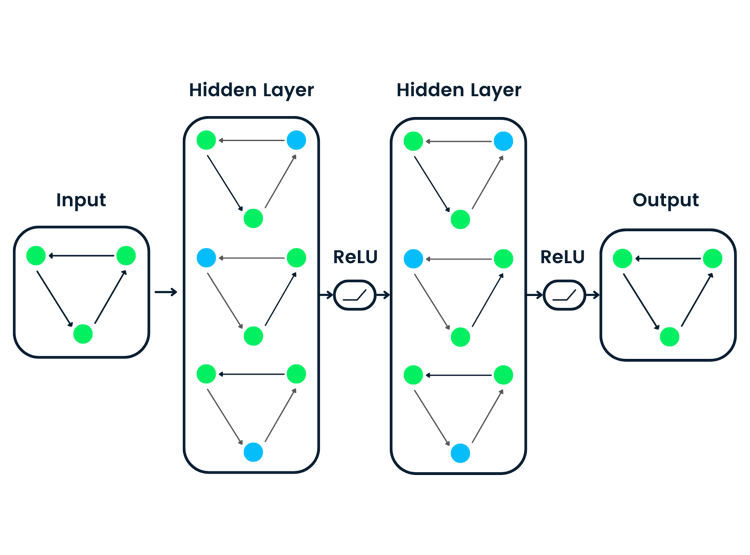
En una MLP hay tres tipos de capas: capa de entrada, capa oculta y capa de salida, como ya hemos mencionado brevemente anteriormente. 

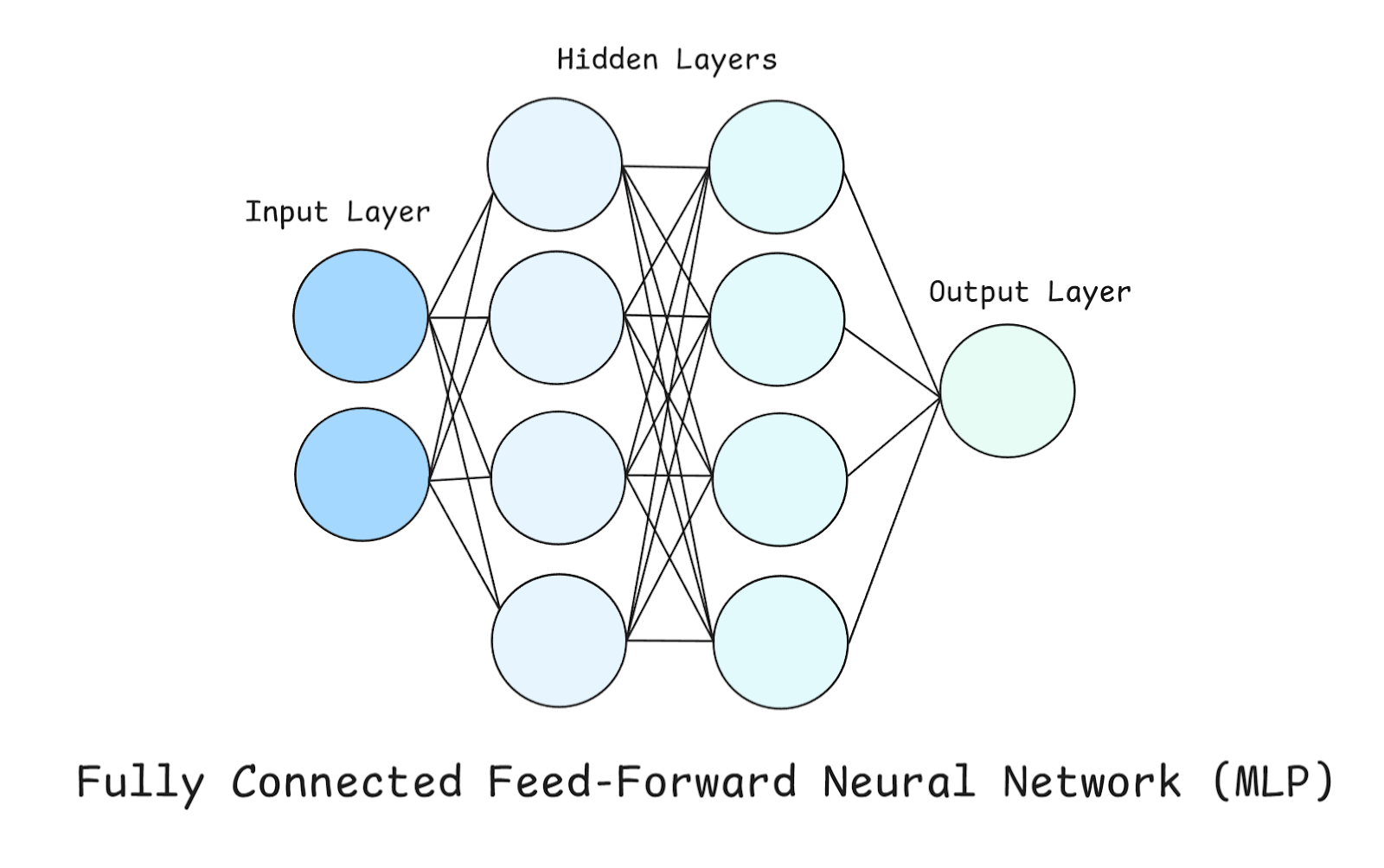
Echa un vistazo al diagrama anterior mientras exploramos estas capas con más detalle. 

Capa de entrada

Este es el punto de entrada de la red.  Cada neurona aquí representa una característica del conjunto de datos. Es importante destacar que la capa de entrada no realiza ningún cálculo por sí misma, sino que simplemente transmite los números sin procesar. En nuestro ejemplo, dado que solo hay dos neuronas en la capa de entrada, esto significa que nuestro conjunto de datos contiene dos características (o que solo estamos considerando dos características de nuestro conjunto de datos). 

Capas ocultas

Estos son donde se realiza el cálculo real. Tenemos dos capas ocultas, cada una con cuatro neuronas. Cada neurona de una capa oculta realiza estas tres funciones:

1. Suma ponderada: Cada entrada se multiplica por un peso y luego se suman todas. 
2. Bias: Se añade un sesgo constante para dar flexibilidad al cambio de función.
3. Función de activación: Se aplica una función de compresión no lineal como ReLU, tanh o sigmoide. Este paso es el que permite a la red aprenderpatrones complejos y no lineales .

Capa de salida

La capa de salida produce la predicción final, y su diseño depende del problema que estemos tratando de resolver:

• Problemas de regresión , como la predicción de los precios de la vivienda. En este caso, la capa de salida contendrá una neurona sin activación (lineal). ¿Por qué lineal? Como no queremos aplastar los valores, los precios de las viviendas podrían ser cualquier número real.
• Problemas de clasificación binaria (decisiones sí/no), como predecir si un correo electrónico es spam o no. Aquí, la capa de salida sería una neurona con una activación sigmoidea. ¿Por qué sigmoide? Esto se debe a que queremos que nuestra red genere valores entre 0 y 1 (ya que estamos prediciendo probabilidades). 
• Problemas de clasificación multiclase (3 o más clases), como clasificar una imagen según los diferentes animales que aparecen en ella. La capa de salida tendríaun , una neurona por clase, con activación softmax. ¿Por qué softmax? Porque convierte las puntuaciones brutas en probabilidades que suman 1 (por ejemplo, 70 % gato, 20 % perro, 10 % caballo).

A modo de referencia, aquí tienes un diagrama que muestra nueve formas comunes de funciones de activación que se utilizan en FFNN y en el aprendizaje profundo en general. 

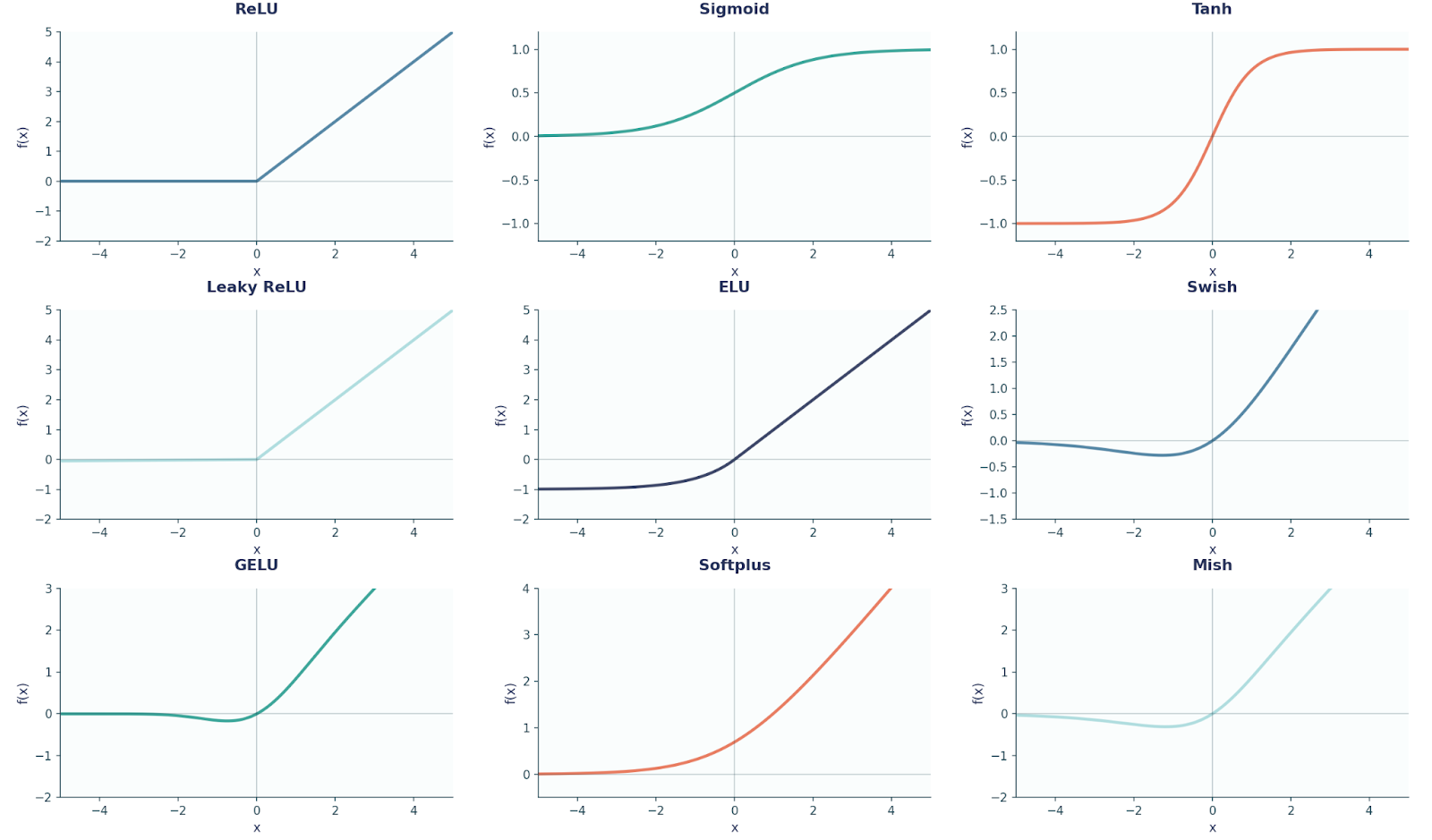
Antes de continuar, también es importante señalar aquí que cada neurona de una capa se conecta con todas las neuronas de la siguiente capa (por eso se dice que están totalmente conectadas).

Volviendo a nuestro ejemplo, tenemos:

Params = (2⋅4+4)+(4⋅4+4)+(4⋅1+1)=12+20+5=37

Cada corchete muestra el número de parámetros entre capas consecutivas, donde se multiplican entre sí el número de neuronas de la capa anterior y el de la capa actual, y luego se suma el número de sesgos (es decir, el número de neuronas de la capa actual). ¡Intenta realizar estos cálculos también con otros ejemplos de redes neuronales para practicar!

Entrenamiento de una red neuronal feedforward

En el aprendizaje profundo, el entrenamiento se divide en dos pasos: paso hacia adelante/propagación y retropropagación. En palabras sencillas, la propagación hacia adelante nos da predicciones, mientras que la retropropagación es la forma en que aprendemos de los errores.

Propagación hacia adelante 

Todo lo que hemos visto hasta ahora se encuentra bajo propagación hacia adelante. En resumen, cuando los datos se mueven a través de una MLP, cada capa realiza los mismos dos pasos, que pueden expresarse matemáticamente mediante estas ecuaciones:

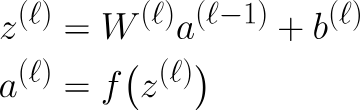
Aquí z es la salida después de multiplicar la salida de la capa anterior por los pesos de la capa actual y sumar el sesgo, también conocido como paso lineal.

Naturalmente, si la capa anterior es la capa de entrada, entonces esto sería x en lugar de al-1. El siguiente paso es elpaso de activación de . Para que esto sea más riguroso desde el punto de vista matemático, podemos escribir los pesos y el sesgo de la siguiente manera:

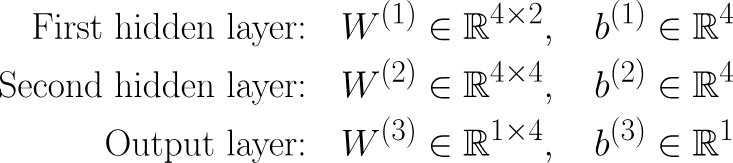
Retropropagación

Cuando recibimos un resultado, ¿cómo le indicamos a nuestra red si es correcto o no? O mejor aún, ¿cómo podemos mejorar la red para que realice mejor nuestra tarea específica? Aquí es donde entra en juego la entra en juego la retropropagación. Podemos considerarlo como el sistema de retroalimentación de la red, que indica al modelo cuán lejos estaba y cómo ajustarse. Podemos desglosarlo así:

1. Compara predicciones: Observa lo que predijo el modelo (ŷ) y cuál fue la respuesta correcta (y).
2. Calcula el error: Utilizamos una función de pérdida para medir cuán errónea fue la predicción, como el MSE.
3. Retropropagación (mediante la regla de la cadena): Se calculan los gradientes con respecto a todos los sesgos y pesos. ∂L/∂w,∂L/∂b .
4. Actualización del método de descenso por gradiente: Los parámetros respectivos se actualizan para reducir las pérdidas utilizando la siguiente regla:

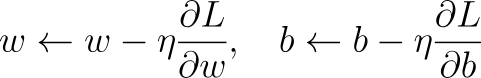
Aquí, η es la tasa de aprendizaje, un parámetro que se puede modificar para determinar la cantidad en que deben cambiar los parámetros en cada actualización.

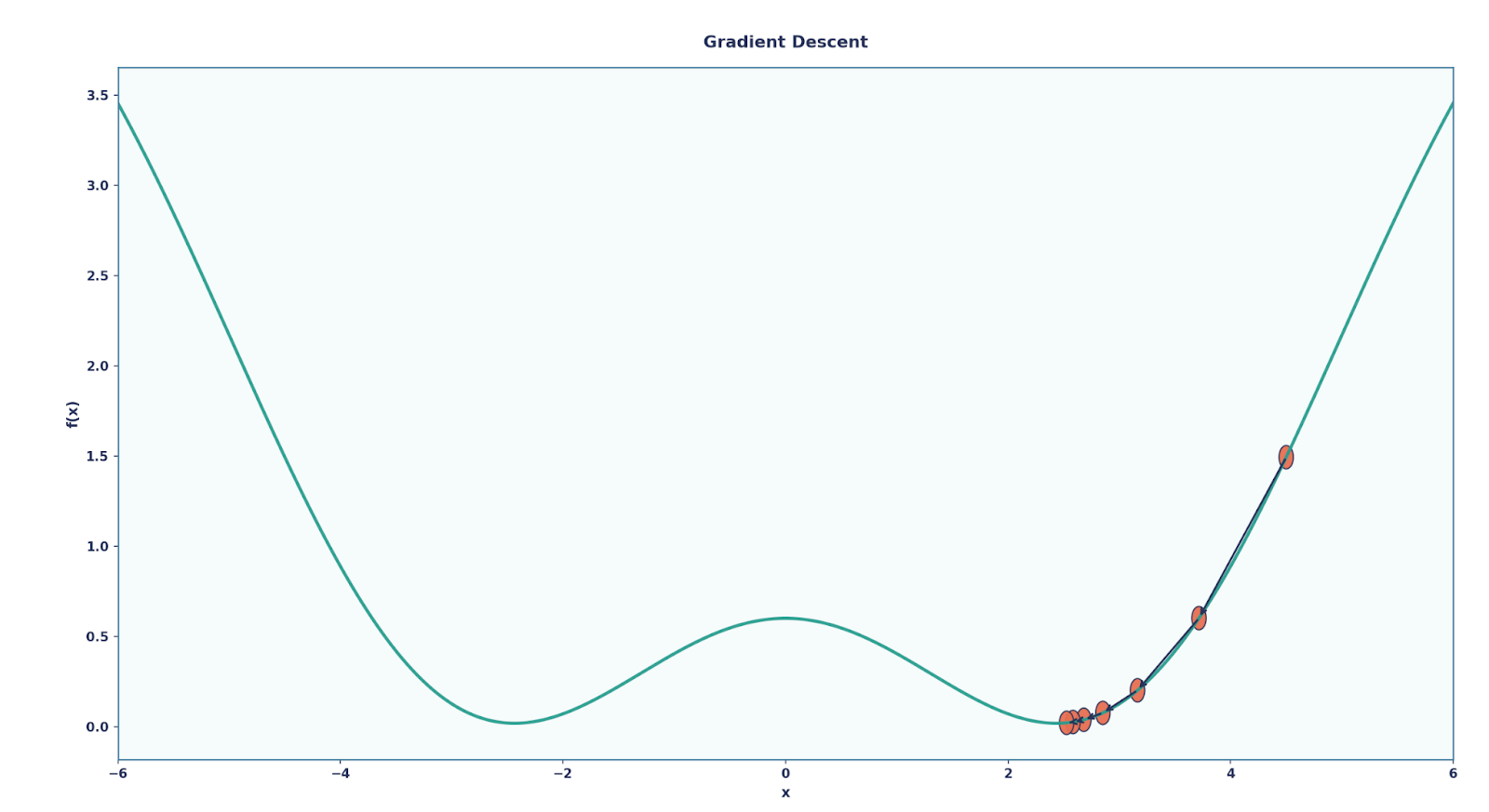
A lo largo de muchas rondas de este proceso, la red aprende y mejora gradualmente en la tarea.

Para que quede más claro, veamos juntos un ejemplo muy sencillo. Supongamos que tenemos:

• Entrada: x = 2
• Salida objetivo: y=4
• Predicción: ŷ = 3

Ahora repasemos los pasos. 

1. Compara la predicción: ŷ =3, y = 4
2. Error: Para este ejemplo, vamos a utilizar el MSE: L=(y−y^​)2=(4−3)2=1
3. Retropropagación: La red calcula cuánto ha contribuido cada peso y sesgo a este error utilizando derivadas y, a continuación, actualizamos cada uno de los parámetros utilizando el paso de actualización de descenso de gradiente. 

Codificación de una red neuronal feed forward en PyTorch

Hemos cubierto las matemáticas relevantes para construir una FFNN (específicamente una MLP). Para seguir avanzando, vamos a programar esto en PyTorch.

Perceptrón multicapa

# Imports we will be needing
import torch
import torch.nn as nn
import torch.optim as optim

X,y = dataset # Here will be our dataset 

# We have created a MLP here using nn.Sequential()
model = nn.Sequential(
    nn.Linear(2, 4),  # input layer → hidden layer (2 → 4)
    nn.ReLU(),        # relu activation function
    nn.Linear(4, 4), # hidden layer 1 → hidden layer 2 (4 → 4)
    nn.ReLU(), 
    nn.Linear(4, 1)   # hidden layer 2 → output (4 → 1)
)


criterion = nn.MSELoss()         # regression loss, i.e our loss function
optimizer = optim.SGD(model.parameters(), lr=0.1) # Optimizer using the Stochastic Gradient Descent

# Training Loop
EPOCHS = 200 # Number of epochs we will be training for
for epoch in range(EPOCHS):
    # Forward pass
    outputs = model(X)
    loss = criterion(outputs, y)

    # Backward pass
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

En este punto, deberías ser capaz de relacionar el código PyTorch con los pasos matemáticos que hemos explorado anteriormente. Sin embargo, es posible que tengas alguna pregunta sobre las épocas.

Un epoch es una pasada completa de todo el conjunto de datos de entrenamiento a través de la red neuronal. Por ejemplo, supongamos que tenemos 1000 puntos de datos de entrenamiento y un tamaño de lote = 100, entonces, después de que la red haya visto las 1000 imágenes (es decir, 10 lotes), eso es una época. El entrenamiento suele requerir muchas épocas para que el modelo pueda seguir mejorando sus pesos.

Red neuronal convolucional

También quiero mencionar brevemente otras FFNN, entre las que destaca una muy famosa: la Red neuronal convolucional (CNN).

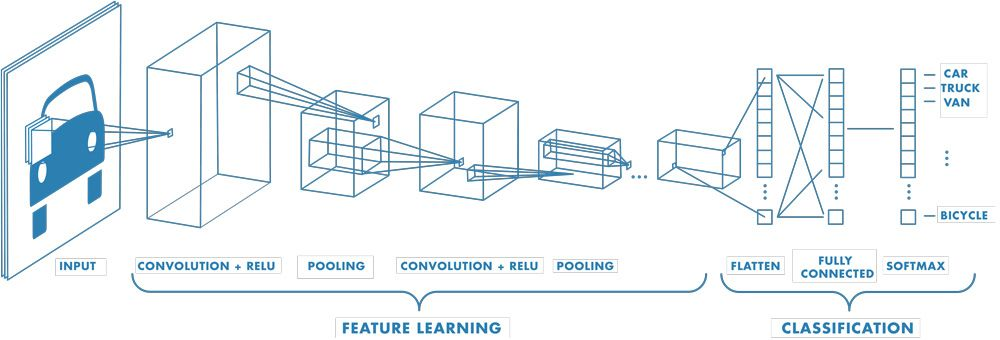
Aunque una CNN también contiene una MLP al final, al principio contiene unas capas especiales llamadas capas convolucionales y capas de agrupación. Hablando primero de las capas convolucionales, estas son esenciales, ya que solo analizan pequeñas regiones locales de la entrada a la vez utilizando unfiltro (o núcleo)e .

Esto resulta muy útil a la hora de clasificar imágenes, ya que:

• Las capas densas habrían tratado cada píxel por separado, ignorando la estructura espacial.
• Las capas convolucionales, por otro lado, pueden detectar bordes, texturas y formas en pequeños fragmentos, y luego combinarlos en patrones más complejos a medida que profundizamos.

Además de las capas convolucionales, las CNN también utilizan capas de agrupamiento.

Es importante señalar que las capas de agrupación no aprenden parámetros, sino que reduce la resolución los mapas de características para hacerlos más pequeños y manejables.

• El más común es Max Pooling, que toma el valor máximo de cada pequeña región (por ejemplo, una ventana de 2×2).
• La agrupación hace que la red sea más eficiente y también proporciona invarianza de traducción (a la red le importa más si una característica existe, no exactamente dónde está).

Podemos programar una CNN utilizando PyTorch de la siguiente manera:

class SimpleCNN(nn.Module): # Define our model as a class
    def __init__(self):
        super().__init__()
        self.conv = nn.Conv2d(1, 8, 3)     # 1→8 channels, 3x3 kernel
        self.pool = nn.MaxPool2d(2, 2)
        self.fc   = nn.Linear(8*13*13, 10) # flatten → 10 classes

    def forward(self, x): # Forward propagation function 
        x = self.pool(torch.relu(self.conv(x)))
        x = x.view(x.size(0), -1)          # flatten
        return self.fc(x)

En el código anterior, hemos creado una CNN muy sencilla, compuesta por una única capa de convolución, una única capa de agrupamiento y una única capa lineal. 

Otros ejemplos de redes neuronales feed-forward

Hemos visto dos ejemplos muy famosos e importantes de FFNN, pero hay muchos más que han supuesto una revolución en sus respectivos campos, como por ejemplo:

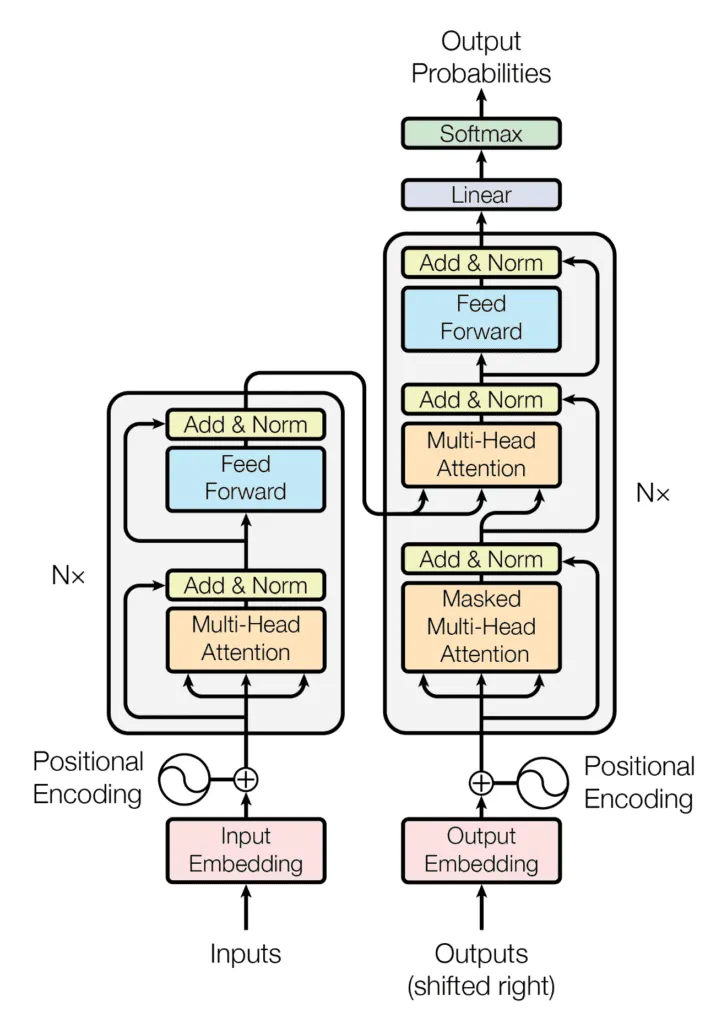
1. Transformers: cada bloque contiene una parte MLP/FFN (después de la autoatención, la «capa de alimentación directa» expande y contrae las dimensiones).
2. Transformadores de visión (ViT): aplican bloques transformadores (con FFNN en su interior) a fragmentos de imágenes.
3. Autoencoders (básicos): codificador + decodificador, ambos construidos a partir de FFNN.
4. Sistemas de recomendación (basados en MLP): por ejemplo, modelos amplios y profundos para clasificaciones y predicciones.

Reflexiones finales

Espero que te hayas dado cuenta de lo importantes que son las FFNN en el campo de la IA. Sin ellos, el panorama actual del aprendizaje profundo no existiría.

Para continuar, te recomiendo encarecidamente dominar la retropropagación y profundizar en las funciones de activación. Dado que esta es la base del aprendizaje profundo, también recomendaría aprender aprendizaje profundo con PyTorch.