Redes Neurais Feed-Forward explicadas: Um tutorial completo

Ao analisar algoritmos de machine learning, poucos conceitos são tão fundamentais quanto a Rede Neural Feed-Forward (FFNN). Se você já criou sua primeira rede neural, é bem provável que tenha sido uma rede feed-forward. Eles podem ser vistos em quase todos os lugares - desde problemas simples de classificação até camadas de potência em arquiteturas profundas.

Primeiro, vou mostrar onde as redes neurais feed-forward se encaixam no esquema geral das coisas:

Neste tutorial, vou explicar o que é uma rede neural feed-forward, como ela evoluiu e por que ainda é relevante hoje em dia, além de explorar exemplos reais.

O que é uma rede neural feed-forward?

Intuitivamente falando, a melhor maneira de descrever essa arquitetura de rede é: “Os dados fluem apenas para frente, sem loops”.

Basicamente, uma FFNN processa os dados de forma que eles fluam numa direção, da entrada para a saída. Não tem looping back, recursão nem ciclos (tirandoa retropropagação e , que vamos ver daqui a pouco).

Quando eu estava começando a aprender sobre isso, a imagem mental que mais me ajudou foi a de uma esteira rolante de fábrica. 

Por quê? 

Porque cada etapa do processo (ou cada camada da rede) faz algo simples com a entrada antes de passar para a próxima.

Funciona assim:

1. As entradas vão para a primeira camada (a camada de entrada).
2. Eles são transformados por pesos e vieses e passam por uma função de ativação.
3. Isso continua através de uma ou mais camadas ocultas.
4. Por fim, a camada de saída faz uma previsão.

Antes de mostrar como é essa arquitetura de rede, quero esclarecer um equívoco comum:

“As redes neurais feed-forward são iguais às MLPs.”

Para esclarecer esse equívoco, precisamos explorar a história inicial do Deep Learning. 

História inicial do aprendizado profundo

Perceptron: Começamos com oPerceptron , que foi inventado nos anos 50 por Frank Rosenblatt. Era um classificador binário de camada única e, embora não conseguisse resolver tudo (como problemas XOR), ele criou as bases para as redes neurais.

Em palavras simples, um perceptron funcionava assim:

1. Contribuições: Cada entrada (como x_1, x_2, etc.) tem um peso associado (w_1, w_2, etc.).
2. Soma ponderada: As entradas são multiplicadas pelos seus pesos e somadas, juntamente com um termo de viés: z = w1*x1 + w2*x2+ ... + b.
3. Ativação: O resultado passa por uma função escalonada (uma ativação). Se o valor estiver acima de um limite, o perceptron gera um 1; caso contrário, gera um 0.

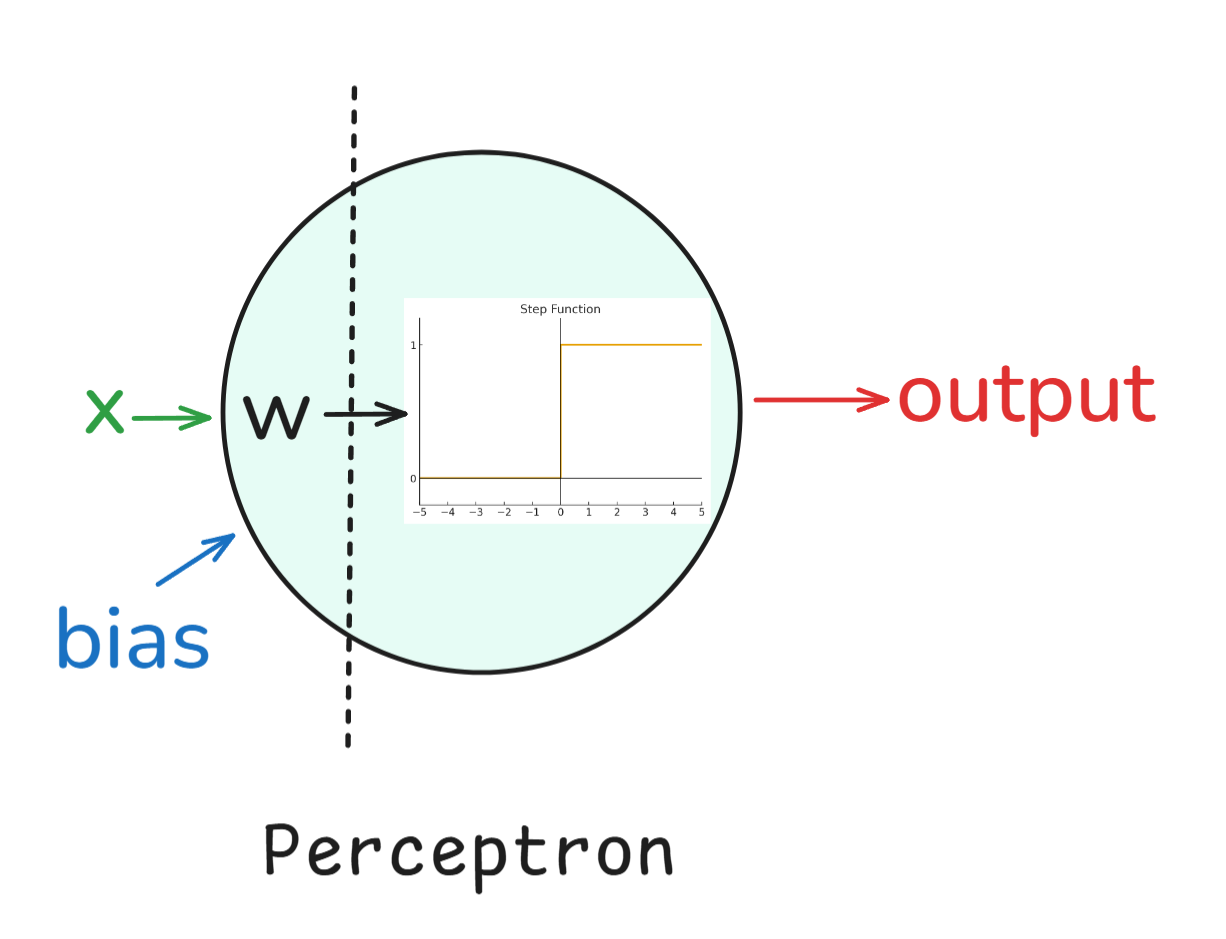
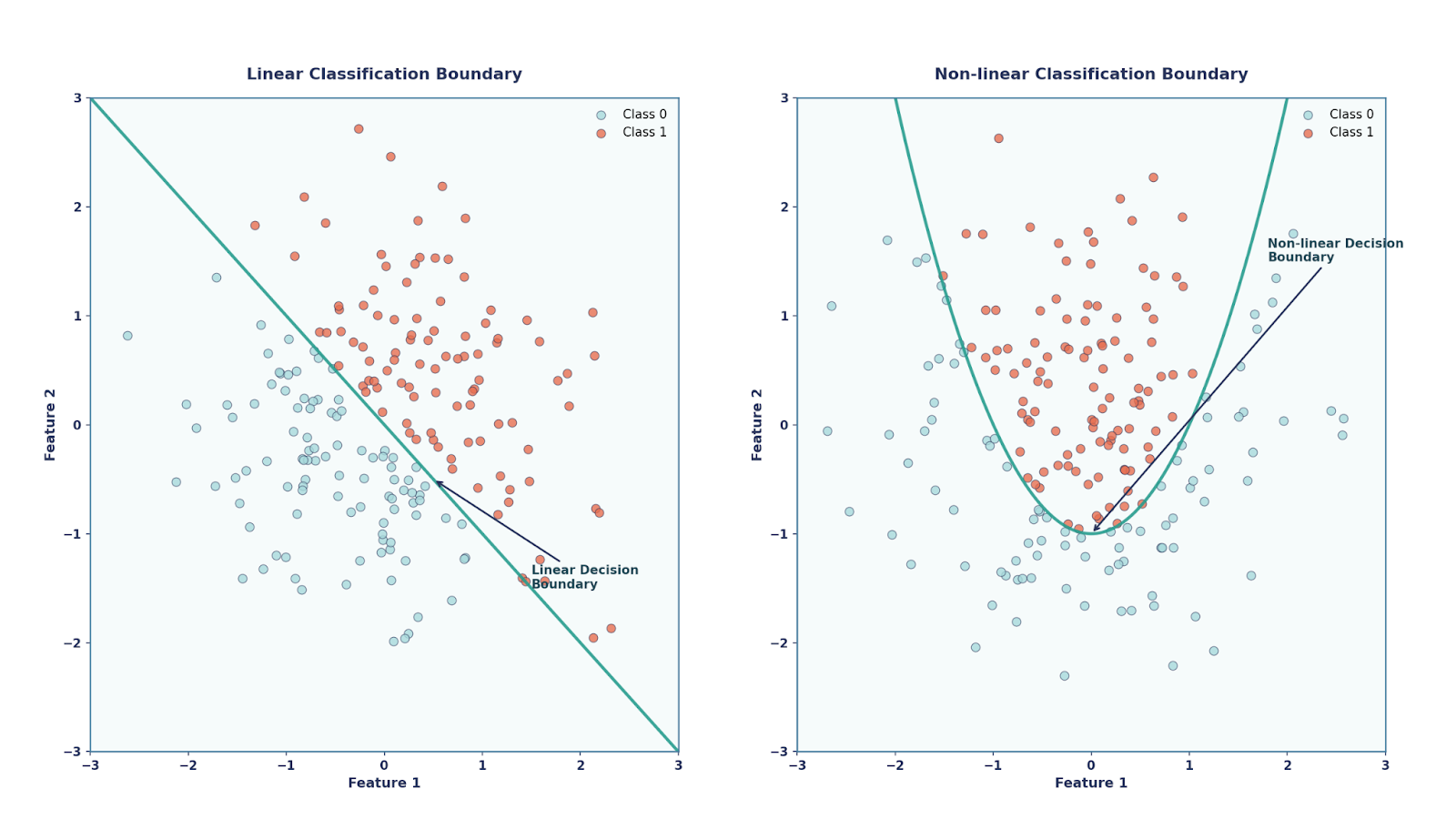
Basicamente, o perceptron é um classificador linear, o que quer dizer que ele só consegue traçar limites de decisão em linha reta (ou hiperplano). Por um lado, o Perceptron tinha seus méritos, como ser muito simples e elegante (já que foi inspirado pela biologia), além de ser computacionalmente barato. Por outro lado, porém, não conseguiu resolver problemas que não são linearmente separáveis, como o problema XOR. 

Perceptrons multicamadas (MLPs): Avançando algumas décadas, nos anos 80, os pesquisadores descobriram que, se você juntasse vários perceptrons e adicionasse funções de ativação não lineares, poderia resolver problemas mais complexos. Essa estrutura ficou conhecida como Perceptron Multicamadas.

Funcionava assim: 

1. Camada de entrada: Peguei as características brutas do conjunto de dados.
2. Camadas ocultas: Uma ou mais camadas de perceptrons que fazem transformações. Cada neurônio fezum e z = w*x + b e passou por uma função de ativação não linear, como sigmoide, tanh, etc.
3. Camada de saída: A camada final produziu a previsão final (por exemplo, probabilidades de classe, valores de regressão).

A adição dessas ativações não lineares foi super importante. Sem eles, as camadas empilhadas simplesmente se transformariam em uma única transformação linear. Com eles, as MLPs podem representar funções super complexas e não lineares.

Isso levou a um dos resultados mais famosos da teoria das redes neurais: o Teorema da Aproximação Universal.

Esse teorema diz que uma rede neural com só uma camada oculta — desde que tenha uma função de ativação não linear e neurônios suficientes — pode aproximar qualquer função contínua em um domínio limitado. 

Era do Deep Learning: Avançando para a década de 2010, entramos na era do aprendizado profundo. Com GPUs e big data, as FFNNs evoluíram para arquiteturas mais profundas e poderosas, formando a base para CNNs, RNNs e Transformers, que é basicamente onde estamos agora.

Então, voltando ao equívoco original, agora sabemos que:

• Rede Neural Feed-Forward (FFNN). A categoria geral de qualquer rede neural em que os dados fluem em uma direção (entrada → oculta → saída), sem loops.
• Perceptron Multicamadas (MLP). Umtipo de FFN (rede neural artificial)chamado “ ” que tem pelo menos uma camada oculta de perceptrons (neurônios com pesos, viés e ativação).

Em outras palavras, todas as MLPs são FFNNs, mas nem todas as FFNNs são MLPs. É super importante lembrar disso. Outro equívoco comum é sobre o perceptron de camada única (ou seja, só entrada para saída).

Um perceptron de camada única é uma FFNN, mas não uma MLP! Só quando a gente adiciona camadas ocultas é que ele vira um MLP.

Essa diferença é importante porque as MLPs podem fazer aproximação de função universal (com unidades ocultas suficientes e funções de ativação não lineares), enquanto os perceptrons simples de camada única são limitados no que podem representar.

Arquitetura de uma rede neural feed-forward

Na seção anterior, aprendemos bastante sobre FFNN, mas, resumindo, eles podem ser vistos como um , uma pilha de transformações simples. Tem vários componentes diferentes que fazem uma FFNN, então vamos ver isso com mais detalhes, principalmente a estrutura MLP. 

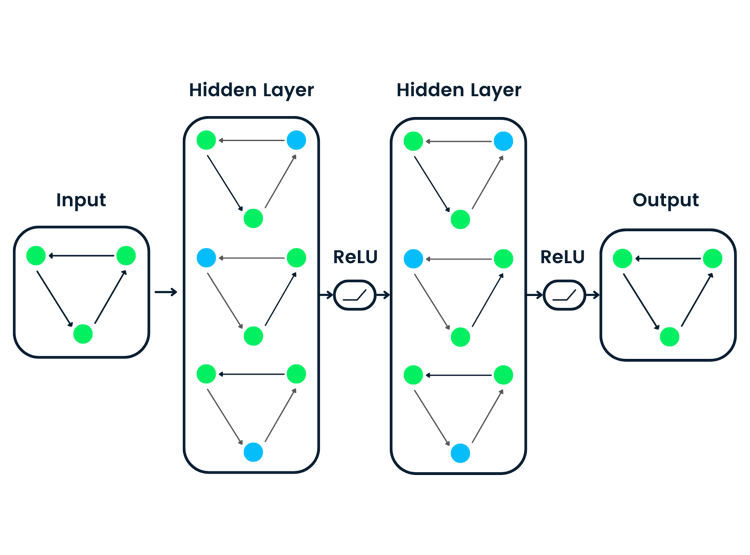
Em uma MLP, tem três tipos de camadas: camada de entrada, camada oculta e camada de saída, que já falamos um pouco antes. 

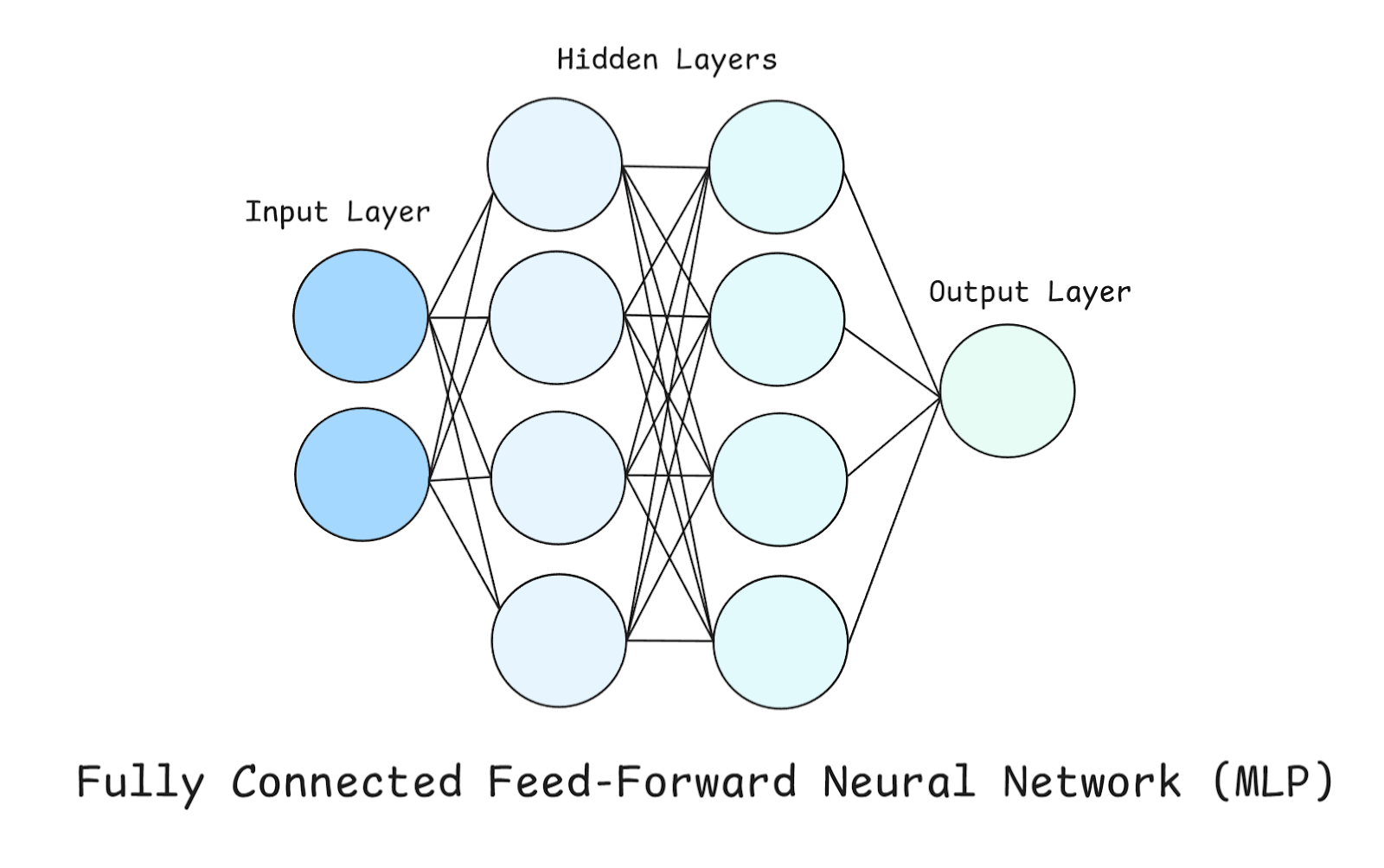
Dá uma olhada no diagrama acima enquanto a gente explora essas camadas com mais detalhes. 

Camada de entrada

Este é o ponto de entrada da rede.  Cada neurônio aqui representauma característica do conjunto de dados. É importante ressaltar que a camada de entrada não faz nenhum cálculo por conta própria — ela só passa os números brutos adiante. No nosso exemplo, como só tem dois neurônios na Camada de Entrada, isso quer dizer que nosso conjunto de dados tem duas características (ou só estamos considerando duas características do nosso conjunto de dados). 

Camadas ocultas

Esses são onde a computação real acontece. Temos duas camadas ocultas, cada uma com quatro neurônios. Cada neurônio em uma camada oculta faz essas três coisas:

1. Soma ponderada: Cada entrada é multiplicada por um peso e, em seguida, todas elas são somadas. 
2. Preconceito: Um viés constante é adicionado para dar flexibilidade na mudança da função.
3. Função de ativação: Uma função de compressão não linear como ReLU, tanh ou sigmoid é aplicada. Essa etapa é o que permite que a rede aprendapadrões complexos e não lineares de um .

Camada de saída

A camada de saída gera a previsão final, e o seu design depende do problema que estamos tentando resolver:

• Problemas de regressão , como prever os preços das casas. Nesse caso, a camada de saída vai ter um neurônio sem ativação (linear). Por que linear? Como não queremos esmagar os valores, os preços das casas podem ser qualquer número real.
• Problemas de classificação binária (decisões sim/não), como prever se um e-mail é spam ou não. Aqui, a camada de saída seria um neurônio com uma ativação sigmoide. Por que sigmoide? Isso porque a gente quer que a nossa rede produza valores entre 0 e 1 (já que estamos prevendo probabilidades). 
• Problemas de classificação multiclasse (3 ou mais classes) — como classificar uma imagem como diferentes animais. A camada de saída teriaum neurônio de e por classe, com ativação softmax. Por que softmax? Porque transforma as pontuações brutas em probabilidades que somam 1 (por exemplo, 70% gato, 20% cachorro, 10% cavalo).

Para sua referência, aqui está um diagrama mostrando nove formas comuns de funções de ativação que são usadas em FFNN e Deep Learning em geral. 

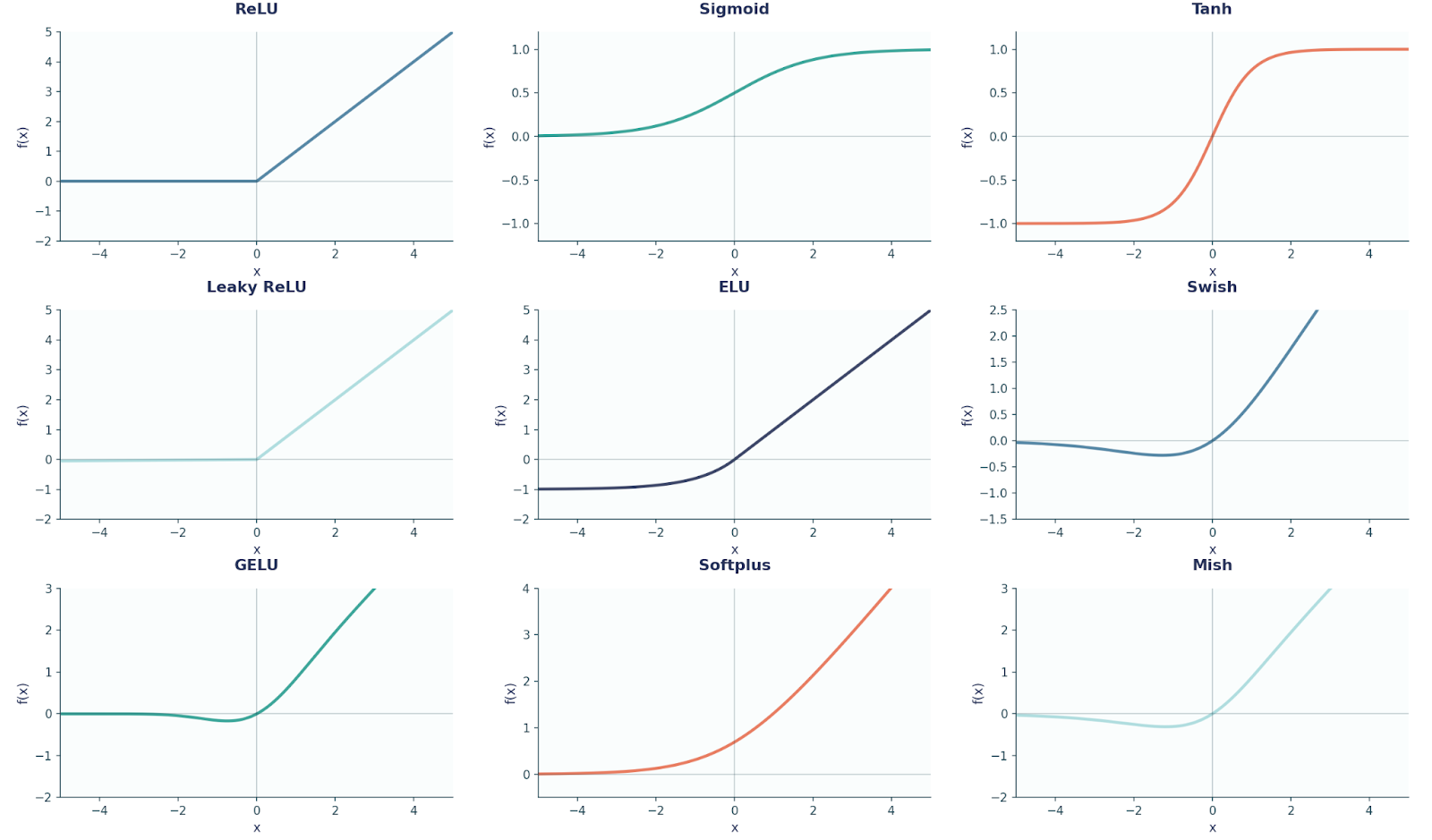
Antes de continuarmos, também é importante notar aqui que cada neurônio em uma camada se conecta a todos os neurônios da camada seguinte (por isso é chamado de totalmente conectado).

Voltando ao nosso exemplo, temos:

Params = (2⋅4+4)+(4⋅4+4)+(4⋅1+1)=12+20+5=37

Cada chave mostra o número de parâmetros entre camadas consecutivas, onde o número de neurônios da camada anterior e da camada atual são multiplicados juntos e, em seguida, o número de vieses (ou seja, o número de neurônios na camada atual) também é adicionado. Tenta fazer esses cálculos em outros exemplos de redes neurais também, pra praticar!

Treinar uma rede neural feedforward

No Deep Learning, o treinamento é dividido em duas etapas: passagem/propagação para frente e retropropagação. Em palavras simples, a propagação para a frente nos dá previsões, enquanto a retropropagação é comoaprendemos com os erros .

Propagação para a frente 

Tudo o que falamos até agora está sob propagação direta. Resumindo, quando os dados passam por uma MLP, cada camada faz as mesmas duas etapas, que podem ser escritas matematicamente por essas equações:

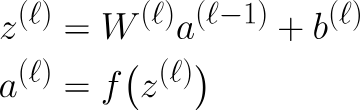
Aqui z é a saída depois de multiplicar a saída da camada anterior pelos pesos da camada atual e somar o viés, também conhecido como Passo Linear.

Claro, se a camada anterior for a camada de entrada, então isso seria x em vez de al-1. O próximo passo é aativação do . Acesse. Para tornar isso mais rigoroso matematicamente, podemos escrever os pesos e o viés assim:

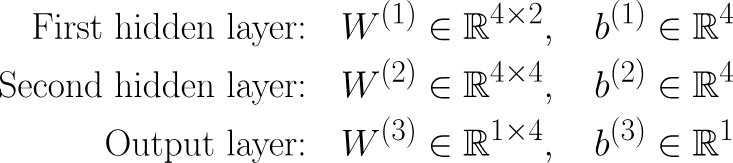
Retropropagação

Quando a gente recebe uma saída, como a gente diz pra nossa rede se ela tá certa ou não? Ou melhor ainda, como podemos melhorar a rede para a nossa tarefa específica? É aqui que entra a a retropropagação entra em cena. Podemos pensar nisso como o sistema de feedback da rede, onde ele diz ao modelo o quanto ele errou e como se ajustar. Podemos explicar assim:

1. Compare as previsões: Olha só o que o modelo previu (ŷ) e qual foi a resposta certa (y).
2. Calcule o erro: Usamos uma função de perda para medir o quão errada foi a previsão, como o MSE.
3. Propagação para trás (via regra da cadeia): Os gradientes em relação a todos os vieses e pesos são calculados. ∂L/∂w,∂L/∂b .
4. Atualização do Gradient Descent: Os parâmetros são atualizados para reduzir a perda usando a seguinte regra:

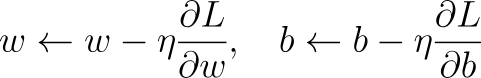
Aqui, η é a taxa de aprendizagem, um parâmetro que pode ser alterado para determinar a quantidade que os parâmetros devem mudar a cada atualização.

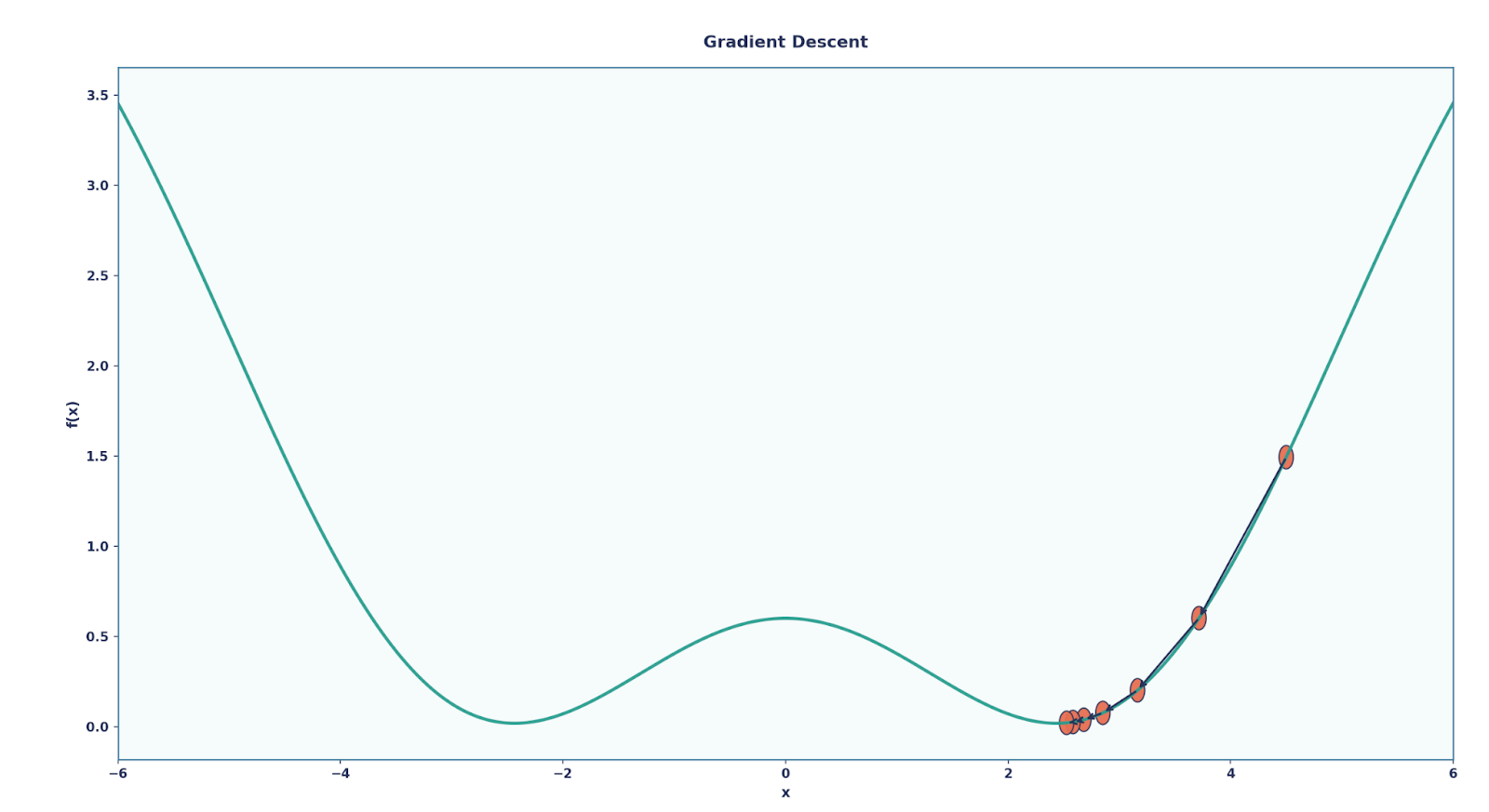
Ao longo de várias rodadas desse processo, a rede vai aprendendo e melhorando na tarefa.

Para deixar tudo mais claro, vamos ver um exemplo bem simples juntos. Digamos que temos:

• Entrada: x = 2
• Saída alvo: y=4
• Previsão: ŷ = 3

Agora vamos ver os passos. 

1. Compare a previsão: ŷ = 3, y = 4
2. Erro: Neste exemplo, vamos usar o MSE: L=(y−y^​)2=(4−3)2=1
3. Retropropagação: A rede descobre quanto cada peso e viés causaram esse erro usando derivadas e, em seguida, atualizamos cada um dos parâmetros usando a etapa de atualização de descida de gradiente. 

Codificando uma rede neural feed forward no PyTorch

A gente já falou sobre a matemática necessária pra construir uma FFNN (mais especificamente, uma MLP). Para avançar ainda mais, vamos codificar isso no PyTorch.

Perceptron multicamadas

# Imports we will be needing
import torch
import torch.nn as nn
import torch.optim as optim

X,y = dataset # Here will be our dataset 

# We have created a MLP here using nn.Sequential()
model = nn.Sequential(
    nn.Linear(2, 4),  # input layer → hidden layer (2 → 4)
    nn.ReLU(),        # relu activation function
    nn.Linear(4, 4), # hidden layer 1 → hidden layer 2 (4 → 4)
    nn.ReLU(), 
    nn.Linear(4, 1)   # hidden layer 2 → output (4 → 1)
)


criterion = nn.MSELoss()         # regression loss, i.e our loss function
optimizer = optim.SGD(model.parameters(), lr=0.1) # Optimizer using the Stochastic Gradient Descent

# Training Loop
EPOCHS = 200 # Number of epochs we will be training for
for epoch in range(EPOCHS):
    # Forward pass
    outputs = model(X)
    loss = criterion(outputs, y)

    # Backward pass
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

Neste ponto, você deve conseguir mapear o código PyTorch para as etapas matemáticas que exploramos antes. Mas, você pode ter alguma dúvida sobre as épocas.

Um epoch é uma passagem completa de todo o conjunto de dados de treinamento pela rede neural. Por exemplo, vamos supor que a gente tenha 1.000 pontos de dados de treinamento e tamanho do lote = 100. Então, depois que a rede tiver visto todas as 1.000 imagens (ou seja, 10 lotes), isso é 1 época. O treinamento geralmente leva muitas épocas para que o modelo possa continuar melhorando seus pesos.

Rede neural convolucional

Também quero falar rapidinho sobre outras FFNNs, sendo uma das mais famosas a Rede Neural Convolucional (CNN).

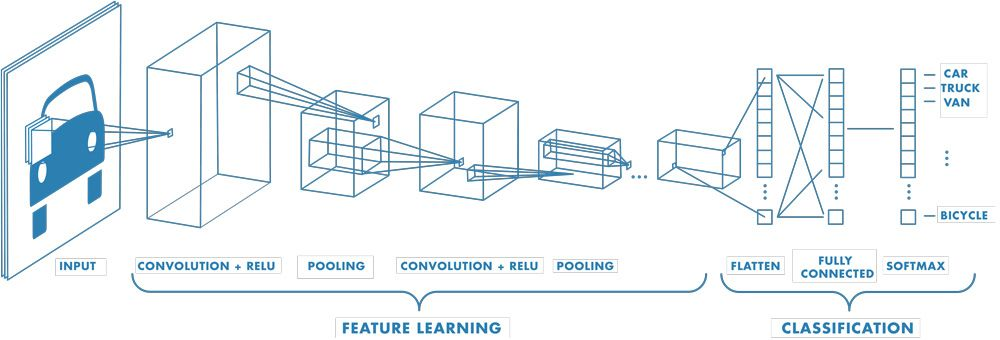
Embora uma CNN também tenha uma MLP no final, no começo ela tem essas camadas especiais chamadas Camadas Convolucionais e Camadas de Pooling. Falando primeiro sobre as camadas convolucionais, elas são essenciais porque analisam apenas pequenas regiões locais da entrada de cada vez, usando umfiltro (ou kernel) .

Isso é muito útil na hora de classificar imagens, porque:

• Camadas densas tratariam cada pixel como separado, ignorando a estrutura espacial.
• Já as camadas convolucionais conseguem detectar bordas, texturas e formas em pequenas áreas — e depois juntam tudo isso em padrões mais complexos à medida que a gente vai aprofundando.

Além das camadas convolucionais, as CNNs também usam camadas de agrupamento.

É importante notar que as camadas de pooling não aprendem parâmetros, mas sim reduzem a resolução os mapas de recursos para torná-los menores e mais gerenciáveis.

• O mais comum é o Max Pooling, que pega o valor máximo de cada pequena região (por exemplo, uma janela 2×2).
• O pooling torna a rede mais eficiente e também proporciona invariância de tradução (a rede se preocupa mais com a existência de uma característica, e não exatamente com a sua localização).

A gente pode programar uma CNN usando o PyTorch assim:

class SimpleCNN(nn.Module): # Define our model as a class
    def __init__(self):
        super().__init__()
        self.conv = nn.Conv2d(1, 8, 3)     # 1→8 channels, 3x3 kernel
        self.pool = nn.MaxPool2d(2, 2)
        self.fc   = nn.Linear(8*13*13, 10) # flatten → 10 classes

    def forward(self, x): # Forward propagation function 
        x = self.pool(torch.relu(self.conv(x)))
        x = x.view(x.size(0), -1)          # flatten
        return self.fc(x)

No código acima, criamos uma CNN bem simples, com uma única camada de convolução, uma única camada de pooling e uma única camada linear. 

Outros exemplos de redes neurais feed-forward

Já falamos sobre dois exemplos bem famosos e importantes de FFNNs, mas tem muitos outros que foram revolucionários nos seus próprios campos, tipo:

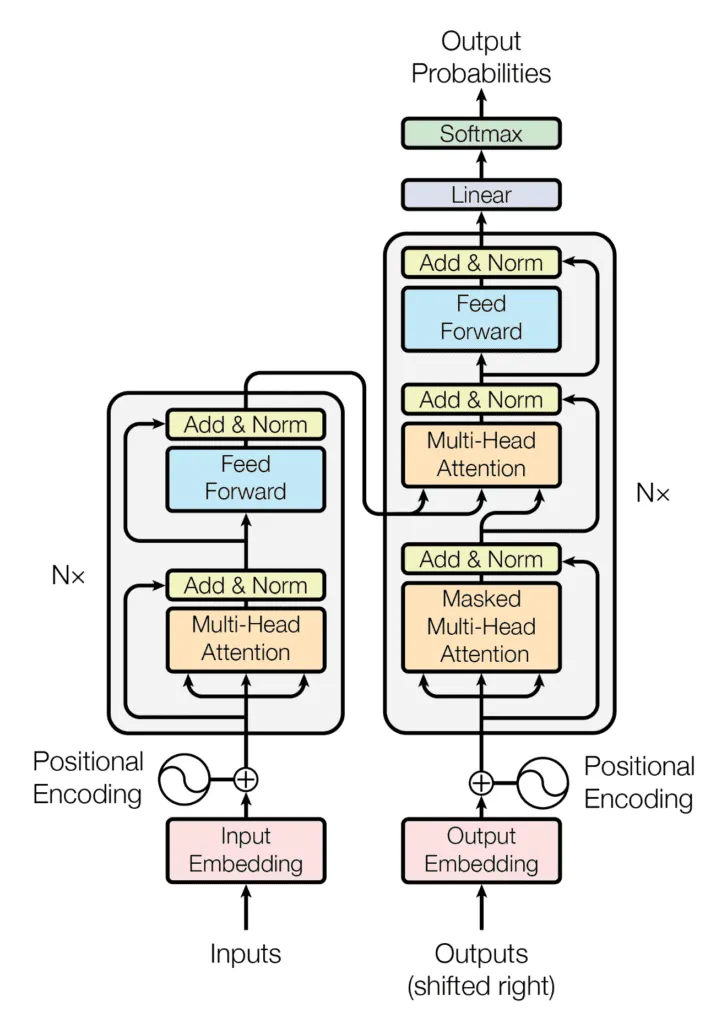
1. Transformers: cada bloco tem uma parte MLP/FFN (depois da autoatenção, a “camada feed-forward” expande + reduz as dimensões).
2. Vision Transformers (ViTs): usam blocos transformadores (com FFNNs dentro) em partes da imagem.
3. Autoencoders (básicos): codificador + decodificador, ambos construídos a partir de FFNNs.
4. Sistemas de recomendação (baseados em MLP): por exemplo, modelos Wide & Deep para classificação e previsões.

Considerações finais

Espero que você tenha percebido como as FFNNs são importantes no campo da IA. Sem eles, o cenário atual do aprendizado profundo não existiria.

Para continuar, eu recomendo muito dominar a retropropagação e se aprofundar nas funções de ativação. Como essa é a base do Deep Learning, eu também recomendo aprender aprendizado profundo com PyTorch.