Perceptrones multicapa en el aprendizaje automático: Guía completa

Fundamentos de las redes neuronales

Las redes neuronales o redes neuronales artificiales son herramientas fundamentales en el aprendizaje automático, que impulsan muchos algoritmos y aplicaciones de vanguardia en diversos ámbitos, como la visión por ordenador, el procesamiento del lenguaje natural, la robótica y otros.

Una red neuronal está formada por nodos interconectados, llamados neuronas, organizados en capas. Cada neurona recibe señales de entrada, realiza un cálculo sobre ellas mediante una función de activación y produce una señal de salida que puede transmitirse a otras neuronas de la red. Una función de activación determina la salida de una neurona dada su entrada. Estas funciones introducen la no linealidad en la red, permitiéndole aprender patrones complejos en los datos.

La red suele organizarse en capas, empezando por la capa de entrada, donde se introducen los datos. Le siguen las capas ocultas, donde se realizan los cálculos y, por último, la capa de salida, donde se hacen las predicciones o se toman las decisiones.

Las neuronas de capas adyacentes están conectadas mediante conexiones ponderadas, que transmiten señales de una capa a la siguiente. La fuerza de estas conexiones, representada por los pesos, determina cuánta influencia tiene la salida de una neurona sobre la entrada de otra. Durante el proceso de entrenamiento, la red aprende a ajustar sus pesos basándose en los ejemplos proporcionados en un conjunto de datos de entrenamiento. Además, cada neurona suele tener un sesgo asociado, que le permite ajustar su umbral de salida.

Las redes neuronales se entrenan mediante técnicas denominadas propagación directa y retropropagación. Durante la propagación directa, los datos de entrada pasan por la red capa por capa, y cada capa realiza un cálculo basado en las entradas que recibe y pasa el resultado a la capa siguiente.

La retropropagación es un algoritmo utilizado para entrenar redes neuronales ajustando iterativamente los pesos y sesgos de la red para minimizar la función de pérdida. Una función de pérdida (también conocida como función de coste o función objetivo) es una medida de lo bien que coinciden las predicciones del modelo con los verdaderos valores objetivo de los datos de entrenamiento. La función de pérdida cuantifica la diferencia entre la salida prevista del modelo y la salida real, proporcionando una señal que guía el proceso de optimización durante el entrenamiento.

El objetivo del entrenamiento de una red neuronal es minimizar esta función de pérdida ajustando los pesos y los sesgos. Los ajustes se guían por un algoritmo de optimización, como el descenso gradiente. Volveremos sobre algunos de estos temas con más detalle más adelante en este tutorial.

Tipos de redes neuronales

Neurona biológica vs. Red neuronal artificial Fuente: ResearchGate

La RNA representada a la derecha de la imagen es una red neuronal simple llamada "perceptrón". Consta de una sola capa, que es la capa de entrada, con múltiples neuronas con sus propios pesos; no hay capas ocultas. El algoritmo del perceptrón aprende los pesos de las señales de entrada para trazar un límite de decisión lineal.

Sin embargo, para resolver problemas más complicados y no lineales relacionados con tareas de procesamiento de imágenes, visión por ordenador y procesamiento del lenguaje natural, trabajamos con redes neuronales profundas.

Consulta el tutorial Introducción a las redes neur onales profundas de Datacamp para aprender más sobre las redes neuronales profundas y cómo construir una desde cero utilizando TensorFlow y Keras en Python. Si prefieres utilizar el lenguaje R, el curso de Datacamp Construir modelos de redes neuronales (NN) en R te ayudará.

Existen varios tipos de RNA, cada una diseñada para tareas y requisitos arquitectónicos específicos. Analicemos brevemente algunos de los tipos más comunes antes de profundizar a continuación en los MLP.

Redes neuronales de avance (FNN)

Son la forma más sencilla de RNA, en las que la información fluye en una dirección, de la entrada a la salida. No hay ciclos ni bucles en la arquitectura de la red. Los perceptrones multicapa (MLP) son un tipo de red neuronal de avance.

Redes neuronales recurrentes (RNN)

En las RNN, las conexiones entre nodos forman ciclos dirigidos, lo que permite que la información persista en el tiempo. Esto los hace adecuados para tareas que implican datos secuenciales, como la predicción de series temporales, el procesamiento del lenguaje natural y el reconocimiento del habla.

Redes neuronales convolucionales (CNN)

Las CNN están diseñadas para procesar eficazmente datos en forma de cuadrícula, como las imágenes. Constan de capas de filtros convolucionales que aprenden representaciones jerárquicas de características dentro de los datos de entrada. Las CNN se utilizan ampliamente en tareas como la clasificación de imágenes, la detección de objetos y la segmentación de imágenes.

Redes de Memoria a Corto Plazo (LSTM) y Unidades Recurrentes Controladas (GRU)

Son tipos especializados de redes neuronales recurrentes diseñadas para resolver el problema del gradiente evanescente en las RNN tradicionales. Las LSTM y las GRU incorporan mecanismos de compuerta para captar mejor las dependencias de largo alcance en los datos secuenciales, lo que las hace especialmente eficaces para tareas como el reconocimiento del habla, la traducción automática y el análisis de sentimientos.

Autocodificador

Está diseñado para el aprendizaje no supervisado y consta de una red codificadora que comprime los datos de entrada en un espacio latente de menor dimensión, y una red decodificadora que reconstruye la entrada original a partir de la representación latente. Los autocodificadores se utilizan a menudo para la reducción de la dimensionalidad, la eliminación de ruido de los datos y el modelado generativo.

Redes Generativas Adversariales (GAN)

Las GAN constan de dos redes neuronales, una generadora y otra discriminadora, entrenadas simultáneamente en un entorno competitivo. El generador aprende a generar muestras de datos sintéticos que no se distinguen de los datos reales, mientras que el discriminador aprende a distinguir entre muestras reales y falsas. Los GAN se han utilizado ampliamente para generar imágenes realistas, vídeos y otros tipos de datos.

Perceptrones multicapa

Un perceptrón multicapa es un tipo de red neuronal feedforward formada por neuronas totalmente conectadas con un tipo de función de activación no lineal. Se utiliza mucho para distinguir datos que no son linealmente separables.

Los MLP se han utilizado ampliamente en diversos campos, como el reconocimiento de imágenes, el procesamiento del lenguaje natural y el reconocimiento del habla, entre otros. Su flexibilidad en la arquitectura y su capacidad para aproximarse a cualquier función en determinadas condiciones los convierten en un elemento fundamental en la investigación sobre el aprendizaje profundo y las redes neuronales. Profundicemos en algunos de sus conceptos clave.

Capa de entrada

La capa de entrada está formada por nodos o neuronas que reciben los datos de entrada iniciales. Cada neurona representa una característica o dimensión de los datos de entrada. El número de neuronas de la capa de entrada viene determinado por la dimensionalidad de los datos de entrada.

Capa oculta

Entre las capas de entrada y salida puede haber una o varias capas de neuronas. Cada neurona de una capa oculta recibe entradas de todas las neuronas de la capa anterior (ya sea la capa de entrada u otra capa oculta) y produce una salida que pasa a la capa siguiente. El número de capas ocultas y el número de neuronas de cada capa oculta son hiperparámetros que deben determinarse durante la fase de diseño del modelo.

Capa de salida

Esta capa está formada por neuronas que producen la salida final de la red. El número de neuronas de la capa de salida depende de la naturaleza de la tarea. En la clasificación binaria, puede haber una o dos neuronas dependiendo de la función de activación y representando la probabilidad de pertenecer a una clase; mientras que en las tareas de clasificación multiclase, puede haber varias neuronas en la capa de salida.

Pesas

Las neuronas de capas adyacentes están totalmente conectadas entre sí. Cada conexión tiene un peso asociado, que determina la fuerza de la conexión. Estos pesos se aprenden durante el proceso de entrenamiento.

Neuronas parciales

Además de las neuronas de entrada y ocultas, cada capa (excepto la de entrada) suele incluir una neurona de polarización que proporciona una entrada constante a las neuronas de la capa siguiente. Las neuronas de sesgo tienen su propio peso asociado a cada conexión, que también se aprende durante el entrenamiento.

La neurona de sesgo desplaza efectivamente la función de activación de las neuronas de la capa siguiente, permitiendo que la red aprenda un desplazamiento o sesgo en el límite de decisión. Ajustando los pesos conectados a la neurona de polarización, la MLP puede aprender a controlar el umbral de activación y ajustarse mejor a los datos de entrenamiento.

Nota: Es importante señalar que, en el contexto de los MLP, el sesgo puede referirse a dos conceptos relacionados pero distintos: el sesgo como término general en el aprendizaje automático y la neurona sesgada (definida anteriormente). En el aprendizaje automático general, el sesgo se refiere al error introducido al aproximar un problema del mundo real con un modelo simplificado. El sesgo mide lo bien que el modelo puede captar los patrones subyacentes en los datos. Un sesgo alto indica que el modelo es demasiado simplista y puede ajustarse mal a los datos, mientras que un sesgo bajo sugiere que el modelo capta bien los patrones subyacentes.

Función de activación

Normalmente, cada neurona de las capas ocultas y de la capa de salida aplica una función de activación a su suma ponderada de entradas. Las funciones de activación habituales son sigmoide, tanh, ReLU (Unidad Lineal Rectificada) y softmax. Estas funciones introducen la no linealidad en la red, permitiéndole aprender patrones complejos en los datos.

Entrenamiento con retropropagación

Los MLP se entrenan mediante el algoritmo de retropropagación, que calcula los gradientes de una función de pérdida con respecto a los parámetros del modelo y actualiza los parámetros iterativamente para minimizar la pérdida.

Funcionamiento de un Perceptrón Multicapa: Capa a capa

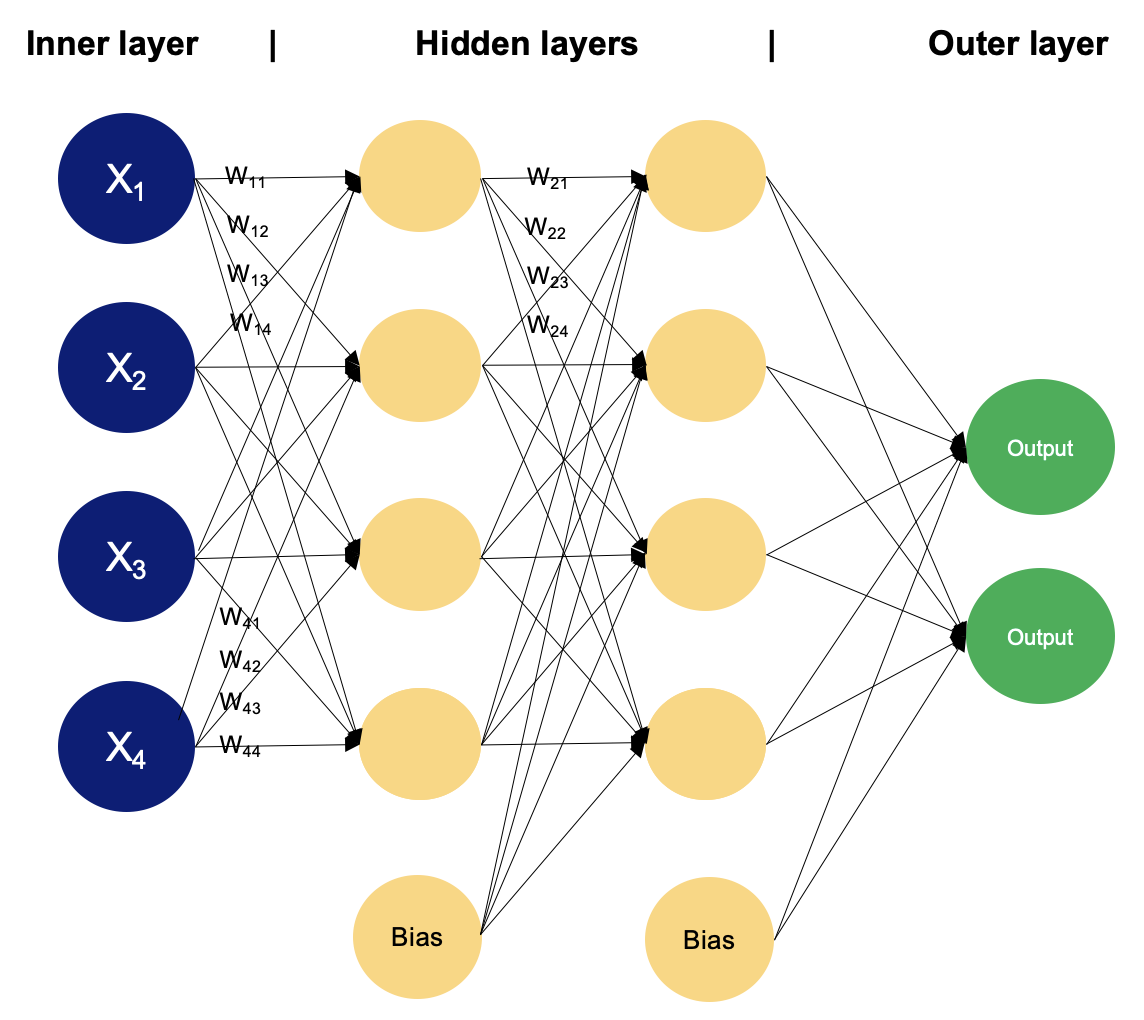
Ejemplo de MLP con dos capas ocultas. Imagen del autor

En un perceptrón multicapa, las neuronas procesan la información paso a paso, realizando cálculos que implican sumas ponderadas y transformaciones no lineales. Caminemos capa por capa para ver la magia que encierra.

Capa de entrada

• La capa de entrada de un MLP recibe datos de entrada, que podrían ser características extraídas de las muestras de entrada de un conjunto de datos. Cada neurona de la capa de entrada representa una característica.

• Las neuronas de la capa de entrada no realizan ningún cálculo; simplemente pasan los valores de entrada a las neuronas de la primera capa oculta.

Capas ocultas

• Las capas ocultas de un MLP están formadas por neuronas interconectadas que realizan cálculos sobre los datos de entrada.

• Cada neurona de una capa oculta recibe información de todas las neuronas de la capa anterior. Las entradas se multiplican por los pesos correspondientes, denotados como w. Los pesos determinan cuánta influencia tiene la entrada de una neurona en la salida de otra.

• Además de los pesos, cada neurona de la capa oculta tiene un sesgo asociado, denotado como b. El sesgo proporciona una entrada adicional a la neurona, permitiéndole ajustar su umbral de salida. Al igual que los pesos, los sesgos se aprenden durante el entrenamiento.
• Para cada neurona de una capa oculta o de la capa de salida, se calcula la suma ponderada de sus entradas. Esto implica multiplicar cada entrada por su peso correspondiente, sumar estos productos y sumar el sesgo:

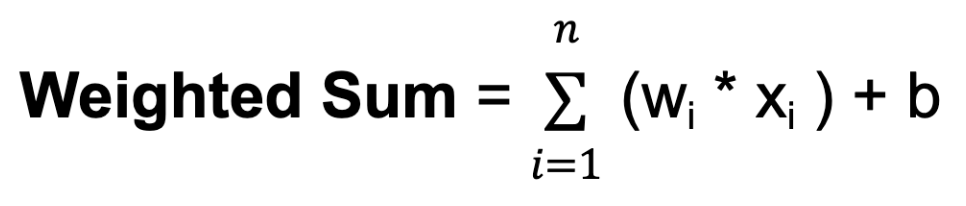
Donde n es el número total de conexiones de entrada, wi es el peso de la entrada i-ésima y xi es el valor de la entrada i-ésima.

• A continuación, la suma ponderada se hace pasar por una función de activación, denominada f. La función de activación introduce la no linealidad en la red, lo que le permite aprender y representar relaciones complejas en los datos. La función de activación determina el rango de salida de la neurona y su comportamiento en respuesta a distintos valores de entrada. La elección de la función de activación depende de la naturaleza de la tarea y de las propiedades deseadas de la red.

Capa de salida

• La capa de salida de un MLP produce las predicciones finales o salidas de la red. El número de neuronas de la capa de salida depende de la tarea que se realice (por ejemplo, clasificación binaria, clasificación multiclase, regresión).

• Cada neurona de la capa de salida recibe la entrada de las neuronas de la última capa oculta y aplica una función de activación. Esta función de activación suele ser distinta de las utilizadas en las capas ocultas y produce el valor final de salida o predicción.

Durante el proceso de entrenamiento, la red aprende a ajustar los pesos asociados a las entradas de cada neurona para minimizar la discrepancia entre las salidas previstas y los verdaderos valores objetivo de los datos de entrenamiento. Ajustando los pesos y aprendiendo las funciones de activación adecuadas, la red aprende a aproximarse a patrones y relaciones complejas en los datos, lo que le permite hacer predicciones precisas sobre muestras nuevas no vistas.

Este ajuste está guiado por un algoritmo de optimización, como el descenso de gradiente estocástico (SGD), que calcula los gradientes de una función de pérdida con respecto a los pesos y actualiza los pesos de forma iterativa.

Veamos más de cerca cómo funciona el SGD.

Descenso Gradiente Estocástico (SGD)

1. Inicialización: El SGD comienza con un conjunto inicial de parámetros del modelo (pesos y sesgos) de forma aleatoria o utilizando algún método predefinido.

2. Optimización iterativa: El objetivo de este paso es encontrar el mínimo de una función de pérdida, moviéndose iterativamente en la dirección de la disminución más pronunciada del valor de la función.

Para cada iteración (o época) de entrenamiento:

• Baraja los datos de entrenamiento para que el modelo no aprenda siempre de los mismos patrones en el mismo orden.
• Divide los datos de entrenamiento en minilotes (pequeños subconjuntos de datos).
• Para cada minilote:
• Calcula el gradiente de la función de pérdida con respecto a los parámetros del modelo utilizando sólo los puntos de datos del minilote. Esta estimación del gradiente es una aproximación estocástica del verdadero gradiente.
• Actualiza los parámetros del modelo dando un paso en la dirección opuesta al gradiente, escalado por una tasa de aprendizaje:Θt+1 = θt - n * ⛛ J (θt)Donde:θt representa los parámetros del modelo en la iteración t. Este parámetro puede ser el peso⛛ J (θt) es el gradiente de la función de pérdida J con respecto a los parámetros θtn es la tasa de aprendizaje, que controla el tamaño de los pasos dados durante la optimización

3. Dirección de descenso: El gradiente de la función de pérdida indica la dirección del ascenso más pronunciado. Para minimizar la función de pérdida, el descenso por gradiente se mueve en la dirección opuesta, hacia el descenso más pronunciado.

4. Ritmo de aprendizaje: El tamaño del paso que se da en cada iteración del descenso gradiente viene determinado por un parámetro llamado tasa de aprendizaje, denotado anteriormente como n. Este parámetro controla el tamaño de los pasos dados hacia el mínimo. Si la tasa de aprendizaje es demasiado pequeña, la convergencia puede ser lenta; si es demasiado grande, el algoritmo puede oscilar o divergir.

5. Convergencia: Repite el proceso durante un número fijo de iteraciones o hasta que se cumpla un criterio de convergencia (por ejemplo, que el cambio en la función de pérdida esté por debajo de un determinado umbral).

El descenso de gradiente estocástico actualiza los parámetros del modelo con mayor frecuencia utilizando subconjuntos más pequeños de datos, lo que lo hace eficiente desde el punto de vista informático, especialmente para grandes conjuntos de datos. La aleatoriedad introducida por el SGD puede tener un efecto de regularización, evitando que el modelo se ajuste en exceso a los datos de entrenamiento. También es adecuado para escenarios de aprendizaje en línea en los que se dispone de nuevos datos de forma incremental, ya que puede actualizar el modelo rápidamente con cada nuevo punto de datos o minilotes.

Sin embargo, el SGD también puede presentar algunos retos, como el aumento del ruido debido a la naturaleza estocástica de la estimación del gradiente y la necesidad de ajustar hiperparámetros como la tasa de aprendizaje. Se han desarrollado varias extensiones y adaptaciones del SGD, como el descenso de gradiente estocástico por mini lotes, el impulso y los métodos de tasa de aprendizaje adaptativa como AdaGrad, RMSProp y Adam, para abordar estos retos y mejorar la convergencia y el rendimiento.

Has visto el funcionamiento de las capas del perceptrón multicapa y has aprendido sobre el descenso en gradiente estocástico; para ponerlo todo junto, hay un último tema en el que sumergirse: la retropropagación.

Retropropagación

Retropropagación es la abreviatura de "propagación de errores hacia atrás". En el contexto de la retropropagación, la SGD consiste en actualizar los parámetros de la red de forma iterativa basándose en los gradientes calculados durante cada lote de datos de entrenamiento. En lugar de calcular los gradientes utilizando todo el conjunto de datos de entrenamiento (lo que puede ser costoso desde el punto de vista informático para grandes conjuntos de datos), el SGD calcula los gradientes utilizando pequeños subconjuntos aleatorios de los datos llamados minilotes. Aquí tienes un resumen de cómo funciona el algoritmo de retropropagación:

1. Pase hacia delante: Durante el paso hacia delante, los datos de entrada se introducen en la red neuronal, y la salida de la red se calcula capa por capa. Cada neurona calcula una suma ponderada de sus entradas, aplica una función de activación al resultado y pasa la salida a las neuronas de la capa siguiente.

2. Cálculo de pérdidas: Tras el paso hacia delante, la salida de la red se compara con los valores objetivo verdaderos, y se calcula una función de pérdida para medir la discrepancia entre la salida prevista y la salida real.

3. Paso atrás (Cálculo del gradiente): En el paso hacia atrás, los gradientes de la función de pérdida con respecto a los parámetros de la red (pesos y sesgos) se calculan utilizando la regla de la cadena del cálculo. Los gradientes representan la tasa de cambio de la función de pérdida con respecto a cada parámetro y proporcionan información sobre cómo ajustar los parámetros para disminuir la pérdida.

4. Actualización de parámetros: Una vez calculados los gradientes, los parámetros de la red se actualizan en la dirección opuesta a los gradientes para minimizar la función de pérdida. Esta actualización se suele realizar mediante un algoritmo de optimización como el descenso de gradiente estocástico (SGD), del que hemos hablado antes.

5. Proceso iterativo: Los pasos 1-4 se repiten iterativamente durante un número fijo de épocas o hasta que se cumplan los criterios de convergencia. Durante cada iteración, los parámetros de la red se ajustan basándose en los gradientes calculados en el paso hacia atrás, reduciendo gradualmente la pérdida y mejorando el rendimiento del modelo.

Preparación de datos para el Perceptrón Multicapa

Preparar los datos para entrenar un MLP implica limpiarlos, preprocesarlos, escalarlos, dividirlos, formatearlos y quizá incluso aumentarlos. Según las funciones de activación utilizadas y la escala de las características de entrada, puede ser necesario normalizar o estandarizar los datos. Experimentar con diferentes técnicas de preprocesamiento y evaluar su impacto en el rendimiento del modelo suele ser necesario para determinar el enfoque más adecuado para un conjunto de datos y una tarea concretos.

• Limpieza y preprocesamiento de datos
• Trata los valores perdidos: Elimina o imputa los valores perdidos en el conjunto de datos.
• Codifica variables categóricas: Convierte variables categóricas en representaciones numéricas, como la codificación de un punto.

• Escalado de características
• Normalización o estandarización: Reescala las características a una escala similar para garantizar que el proceso de optimización converge de forma eficaz.
• Estandarización (normalización de la puntuación Z): Resta la media y divide por la desviación típica de cada característica. Centra los datos en torno a cero y los escala para que tengan varianza unitaria.
• Normalización (escala Mín-Máx): Escala las características a un intervalo fijo, normalmente entre 0 y 1, restando el valor mínimo y dividiéndolo por el intervalo (max-min).

Para aprender más sobre el escalado de características, consulta el curso de Datacamp Ingeniería de Características para el Aprendizaje Automático en Python.

• División Entrenamiento-Validación-Prueba
• Divide el conjunto de datos en conjuntos de entrenamiento, validación y prueba. El conjunto de entrenamiento se utiliza para entrenar el modelo, el conjunto de validación se utiliza para ajustar los hiperparámetros y controlar el rendimiento del modelo, y el conjunto de prueba se utiliza para evaluar el rendimiento final del modelo en datos no vistos.

• Formateo de datos
• Asegúrate de que los datos están en el formato adecuado para la formación. Esto puede implicar remodelar los datos o convertirlos al tipo de datos requerido (por ejemplo, convertir variables categóricas en numéricas).

• Aumento opcional de datos
• Para tareas como la clasificación de imágenes, pueden aplicarse técnicas de aumento de datos como la rotación, el volteo y el escalado para aumentar la diversidad de los datos de entrenamiento y mejorar la generalización del modelo.

• Funciones de normalización y activación
• La elección entre normalización y estandarización puede depender de las funciones de activación utilizadas en el MLP. Las funciones de activación como sigmoide y tanh son sensibles a la escala de los datos de entrada y pueden beneficiarse de la normalización. Por otra parte, las funciones de activación como ReLU son menos sensibles a la escala y puede que no requieran normalización.

Pautas generales para implementar un perceptrón multicapa

Implementar un MLP implica varios pasos, desde el preprocesamiento de los datos hasta el entrenamiento y la evaluación del modelo. Seleccionar el número de capas y neuronas para un MLP implica equilibrar la complejidad del modelo, el tiempo de entrenamiento y el rendimiento de generalización. No existe una respuesta única, ya que la arquitectura óptima depende de factores como la complejidad de la tarea, la cantidad de datos disponibles y los recursos informáticos. Sin embargo, aquí tienes algunas directrices generales que debes tener en cuenta al poner en práctica la MLP:

1. Arquitectura modelo

• Empieza con una arquitectura sencilla y aumenta gradualmente la complejidad según sea necesario. Empieza con una sola capa oculta y un número reducido de neuronas, y luego experimenta añadiendo más capas y neuronas si es necesario.

2. Complejidad de la tarea

• Para tareas sencillas con una complejidad relativamente baja, como la clasificación binaria o la regresión en conjuntos de datos pequeños, puede bastar una arquitectura poco profunda con menos capas y neuronas.
• Para tareas más complejas, como la clasificación o regresión multiclase en datos de alta dimensión, pueden ser necesarias arquitecturas más profundas con más capas y neuronas para captar patrones intrincados en los datos.

3. Preprocesamiento de datos

• Limpia y preprocesa tus datos, incluyendo el tratamiento de valores perdidos, la codificación de variables categóricas y el escalado de características numéricas.
• Divide tus datos en conjuntos de entrenamiento, validación y prueba para evaluar el rendimiento del modelo.

4. Inicialización

• Inicializa adecuadamente los pesos y sesgos de tu MLP. Las técnicas habituales de inicialización incluyen la inicialización aleatoria con pesos pequeños o el uso de técnicas como la inicialización de Xavier o He.

5. Experimentación

• En última instancia, lo mejor es experimentar con distintas arquitecturas, variando el número de capas y neuronas, y evaluar su rendimiento empíricamente.
• Utiliza técnicas como la validación cruzada y el ajuste de hiperparámetros para explorar sistemáticamente distintas arquitecturas y encontrar la que mejor se adapte a la tarea en cuestión.

6. Formación

• Entrena tu MLP utilizando los datos de entrenamiento y controla su rendimiento en el conjunto de validación.
• Experimenta con diferentes tamaños de lote, número de épocas y otros hiperparámetros para encontrar los ajustes óptimos de entrenamiento.
• Visualiza el progreso del entrenamiento utilizando métricas como la pérdida y la precisión para diagnosticar problemas y seguir la convergencia.

7. Algoritmo de optimización

• Experimenta con diferentes ritmos de aprendizaje y considera la posibilidad de utilizar técnicas como la programación de los ritmos de aprendizaje o los ritmos de aprendizaje adaptativos.

8. Evitar el sobreajuste

• Ten cuidado de no sobreajustar el modelo a los datos de entrenamiento introduciendo una complejidad innecesaria.
• Utiliza técnicas como la regularización (por ejemplo, regularización L1, L2), el abandono y la detención temprana para evitar el sobreajuste y mejorar el rendimiento de la generalización.
• Ajusta la fuerza de regularización basándote en el rendimiento del modelo en el conjunto de validación.

9. Evaluación del modelo

• Controla el rendimiento del modelo en un conjunto de validación separado durante el entrenamiento para evaluar cómo afectan al rendimiento los cambios en la arquitectura.
• Evalúa el modelo entrenado en el conjunto de pruebas para valorar su rendimiento de generalización.
• Utiliza métricas como la precisión, la pérdida y el error de validación para evaluar el rendimiento del modelo y orientar las decisiones arquitectónicas.

10. Iterar y experimentar

• Experimenta con diferentes arquitecturas, hiperparámetros y estrategias de optimización para mejorar el rendimiento del modelo.
• Perfecciona tu aplicación basándote en la información obtenida de los resultados de la formación y la evaluación.

Conclusión

Los perceptrones multicapa representan una clase fundamental y versátil de redes neuronales artificiales que han contribuido significativamente al avance del aprendizaje automático y la inteligencia artificial. A través de sus capas interconectadas de neuronas y funciones de activación no lineales, los MLP son capaces de aprender patrones y relaciones complejas en los datos, lo que los hace muy adecuados para una amplia gama de tareas. La historia de los MLP refleja un viaje de exploración, descubrimiento e innovación, desde los primeros modelos de perceptrón hasta las modernas arquitecturas de aprendizaje profundo que impulsan muchos sistemas de última generación en la actualidad.

En este artículo, has aprendido los fundamentos de las redes neuronales artificiales, te has centrado en los perceptrones multicapa, has conocido el descenso de gradiente estocástico y la retropropagación. Si estás interesado en adquirir experiencia práctica y utilizar técnicas de aprendizaje profundo para resolver retos del mundo real, como predecir el precio de la vivienda o crear redes neuronales para modelar imágenes y texto, te recomendamos encarecidamente que sigas el curso sobre la caja de herramientas Keras de Datacamp.

Trabajando con Keras, aprenderás sobre redes neuronales, flujos de trabajo de modelos de aprendizaje profundo y cómo optimizar tus modelos. Datacamp también tiene una hoja de trucos de Keras que puede ser muy útil.