Feed-Forward-Neuralnetzwerke erklärt: Ein komplettes Tutorial

Beim Blick auf Algorithmen für maschinelles Lernengibt es kaum ein Konzept, das so grundlegend ist wie das Feed-Forward Neural Network (FFNN). Wenn du schon mal dein erstes neuronales Netzwerk gebaut hast, war es wahrscheinlich ein Feedforward-Netzwerk. Man sieht sie fast überall – von einfachen Klassifizierungsproblemen bis hin zu Leistungsschichten in tiefen Architekturen.

Lass mich dir erst mal zeigen, wo Feed-Forward-Neuralnetzwerke im großen Ganzen reinhören:

In diesem Tutorial erkläre ich, was ein Feed-Forward-Neuralnetzwerk eigentlich ist, wie es entstanden ist und warum es auch heute noch wichtig ist. Außerdem schaue ich mir Beispiele aus der Praxis an.

Was ist ein Feed-Forward-Neuralnetzwerk?

Einfach gesagt, kann man so eine Netzwerkarchitektur am besten so beschreiben: „Daten fließen nur vorwärts, keine Schleifen.“

Im Grunde verarbeitet ein FFNN Daten so, dass sie in eine Richtung fließen, von der Eingabe zur Ausgabe. Es gibt keine Rückkopplung, keine Rekursion und keine Zyklen (außerder Backpropagation, auf die wir gleich noch eingehen werden).

Als ich das zum ersten Mal gelernt habe, war das Bild, das mir am meisten geholfen hat, ein Fließband in einer Fabrik. 

Warum? 

Weil jeder Schritt im Prozess (oder jede Schicht im Netzwerk) was Einfaches mit der Eingabe macht, bevor er sie an den nächsten weitergibt.

So geht's:

1. Die Eingaben kommen in die erste Schicht (die Eingabeschicht).
2. Sie werden durch Gewichte und Bias verändert und durch eine Aktivierungsfunktion geschickt.
3. Das geht weiter durch eine oder mehrere versteckte Schichten.
4. Schließlich macht die Ausgabeschicht eine Vorhersage.

Bevor ich dir zeige, wie so eine Netzwerkarchitektur aussieht, möchte ich ein weit verbreitetes Missverständnis ausräumen:

„Feed-Forward-Neuralnetzwerke sind dasselbe wie MLPs.“

Um dieses Missverständnis auszuräumen, müssen wir uns mit den Anfängen des Deep Learning beschäftigen. 

Die Anfänge des Deep Learning

Perzeptron: Wir fangen mit dem„ Perceptron” an, das in den 1950er Jahren von Frank Rosenblatt erfunden wurde. Es war ein einlagiger binärer Klassifikator, und obwohl er nicht alles lösen konnte (wie XOR-Probleme), hat er die Basis für neuronale Netze geschaffen.

Einfach gesagt, hat ein Perzeptron so funktioniert:

1. Eingaben: Jeder Input (wie x_1, x_2 usw.) hat ein zugehöriges Gewicht (w_1, w_2 usw.).
2. Gewichtete Summe: Die Eingaben werden mit ihren Gewichten multipliziert und zusammen mit einem Bias-Term addiert: z = w1*x1 + w2*x2+ ... + b.
3. Aktivierungs-: Das Ergebnis wird durch eine Sprungfunktion (eine Aktivierung) geschickt. Wenn der Wert über einem Schwellenwert liegt, gibt das Perzeptron eine 1 aus, sonst eine 0.

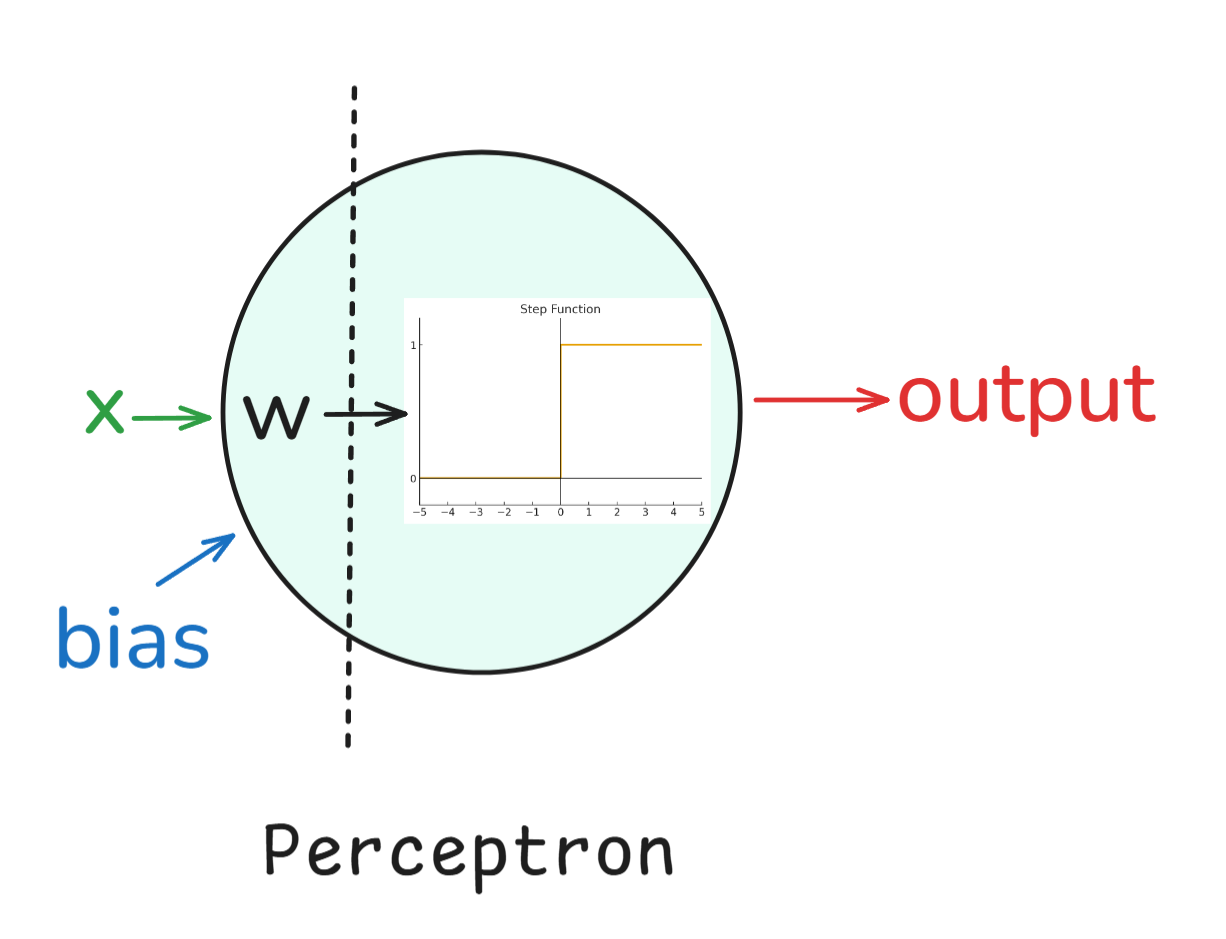
Im Grunde ist das Perzeptron ein linearer Klassifikator, was bedeutet, dass es nur gerade Linien (oder Hyperflächen) als Entscheidungsgrenzen ziehen kann. Einerseits hatte das Perzeptron seine Vorteile, wie zum Beispiel, dass es sehr einfach und elegant war (weil es von der Biologie inspiriert war) und dass es rechnerisch günstig war. Andererseits kann es aber Probleme, die nicht linear trennbar sind, wie zum Beispiel das XOR-Problem, nicht lösen. 

Mehrschichtige Perzeptrons (MLPs): Ein paar Jahrzehnte später, in den 1980er Jahren, haben Forscher rausgefunden, dass man komplexere Probleme lösen kann, wenn man mehrere Perzeptrons stapelt und nichtlineare Aktivierungsfunktionen hinzufügt. Diese Struktur wurde als Mehrschicht-Perzeptronbekannt.

So hat's funktioniert: 

1. Eingabeschicht-: Hab die rohen Features aus dem Datensatz genommen.
2. Versteckte Ebenen: Eine oder mehrere Schichten von Perzeptronen, die Transformationen anwenden. Jedes Neuron hat die Formel„ “ z = w*x + b angewendet und das Ergebnis durch eine nichtlineare Aktivierungsfunktion wie Sigmoid, Tanh usw. geschickt .
3. Ausgabeschicht-: Die letzte Schicht hat die endgültige Vorhersage gemacht (z. B. Klassenwahrscheinlichkeiten, Regressionswerte).

Die Hinzufügung dieser nichtlinearen Aktivierungen war echt wichtig. Ohne sie würde das Stapeln von Schichten einfach zu einer einzigen linearen Transformation zusammenfallen. Mit ihnen könnten MLPs echt komplexe, nichtlineare Funktionen darstellen.

Das führte zu einem der bekanntesten Ergebnisse in der Theorie der neuronalen Netze: dem Satz der universellen Approximation.

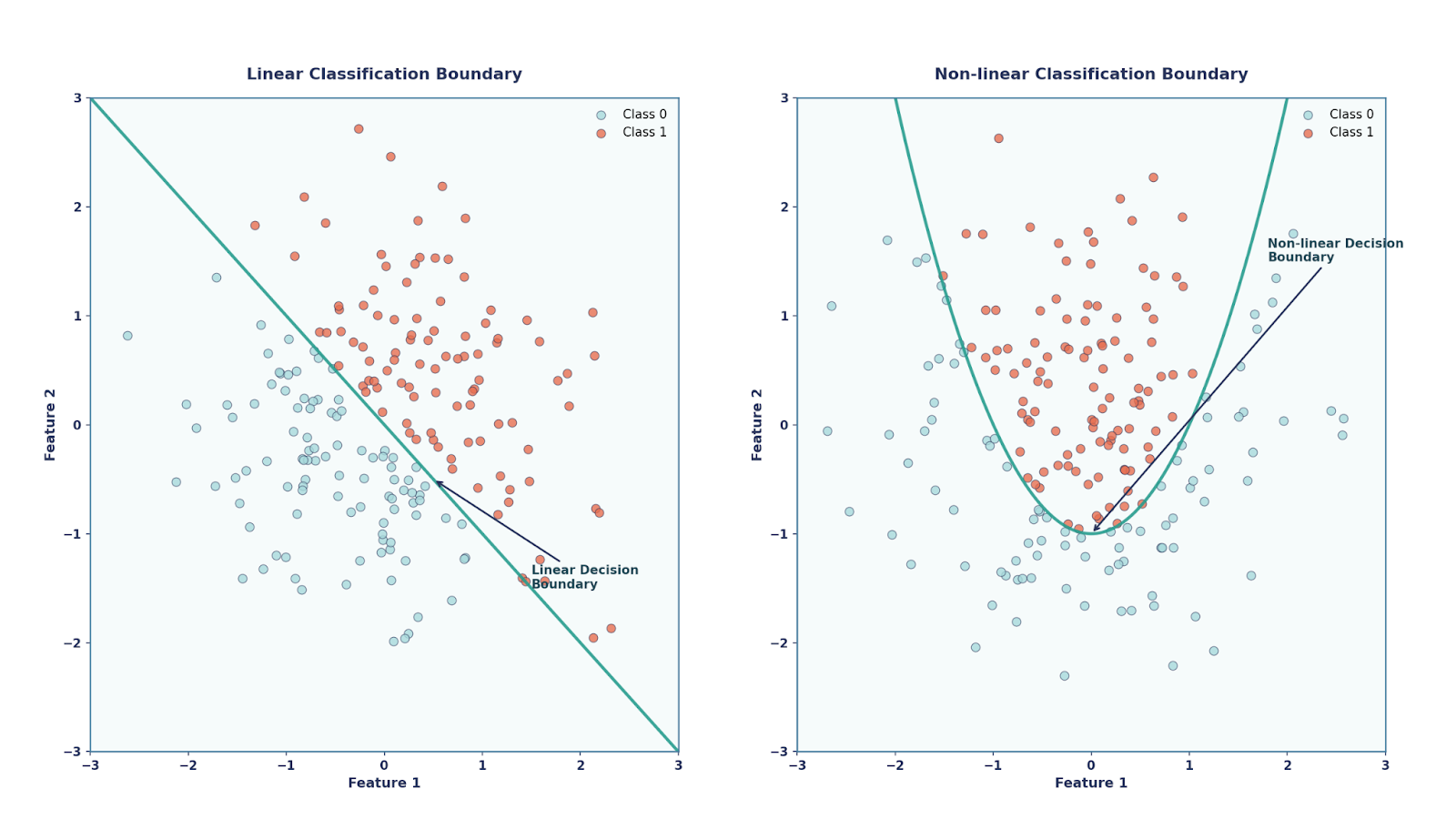
Dieses Theorem besagt, dass ein neuronales Netzwerk mit nur einer einzigen versteckten Schicht – solange es eine nichtlineare Aktivierungsfunktion und genügend Neuronen hat – jede kontinuierliche Funktion auf einem begrenzten Bereich annähern kann. 

Zeitalter des Deep Learning: Mit dem Start in die 2010er Jahre kommen wir ins Zeitalter des Deep Learning. Mit GPUs und Big Data haben sich FFNNs zu tieferen und leistungsfähigeren Architekturen entwickelt und bilden die Grundlage für CNNs, RNNs und Transformatoren, wo wir im Grunde genommen jetzt stehen.

Also, zurück zu dem ursprünglichen Irrtum: Wir wissen jetzt:

• Feed-Forward-Neuralnetzwerk (FFNN). Die allgemeine Kategorie aller neuronalen Netze, bei denen die Daten in eine Richtung fließen (Eingabe → versteckt → Ausgabe), ohne Schleifen.
• Mehrschichtiges Perzeptron (MLP). EinFFN vom Typ „ “ , der mindestens eine versteckte Schicht von Perzeptronen (Neuronen mit Gewichten, Vorspannung und Aktivierung)hat .

Mit anderen Worten: sind alle MLP-Netzwerke FFNNs, aber nicht alle FFNNs sind MLP-Netzwerke. Das ist echt wichtig, sich das zu merken. Ein weiteres häufiges Missverständnis betrifft das einlagige Perzeptron (also nur Eingabe zu Ausgabe).

Ein einlagiges Perzeptron ist ein FFNN, aber kein MLP! Erst wenn wir versteckte Schichten hinzufügen, wird es zu einem MLP.

Dieser Unterschied ist wichtig, weil MLPs universelle Funktionsapproximation können. universelle Funktionsapproximation (mit genügend versteckten Einheiten und nichtlinearen Aktivierungsfunktionen), während einfache einlagige Perzeptrons in ihrer Darstellungsfähigkeit eingeschränkt sind.

Architektur eines Feed-Forward-Neuralnetzwerks

Im letzten Abschnitt haben wir viel über FFNN gelernt, aber einfach gesagt kann man sie sich als „ “ vorstellen, also als eine Reihe einfacher Transformationen. Es gibt viele verschiedene Teile, die ein FFNN ausmachen. Schauen wir uns diese genauer an, vor allem die MLP-Struktur. 

In einem MLP gibt's drei Arten von Schichten: Eingabe-, versteckte und Ausgabeschicht, die wir schon kurz erwähnt haben. 

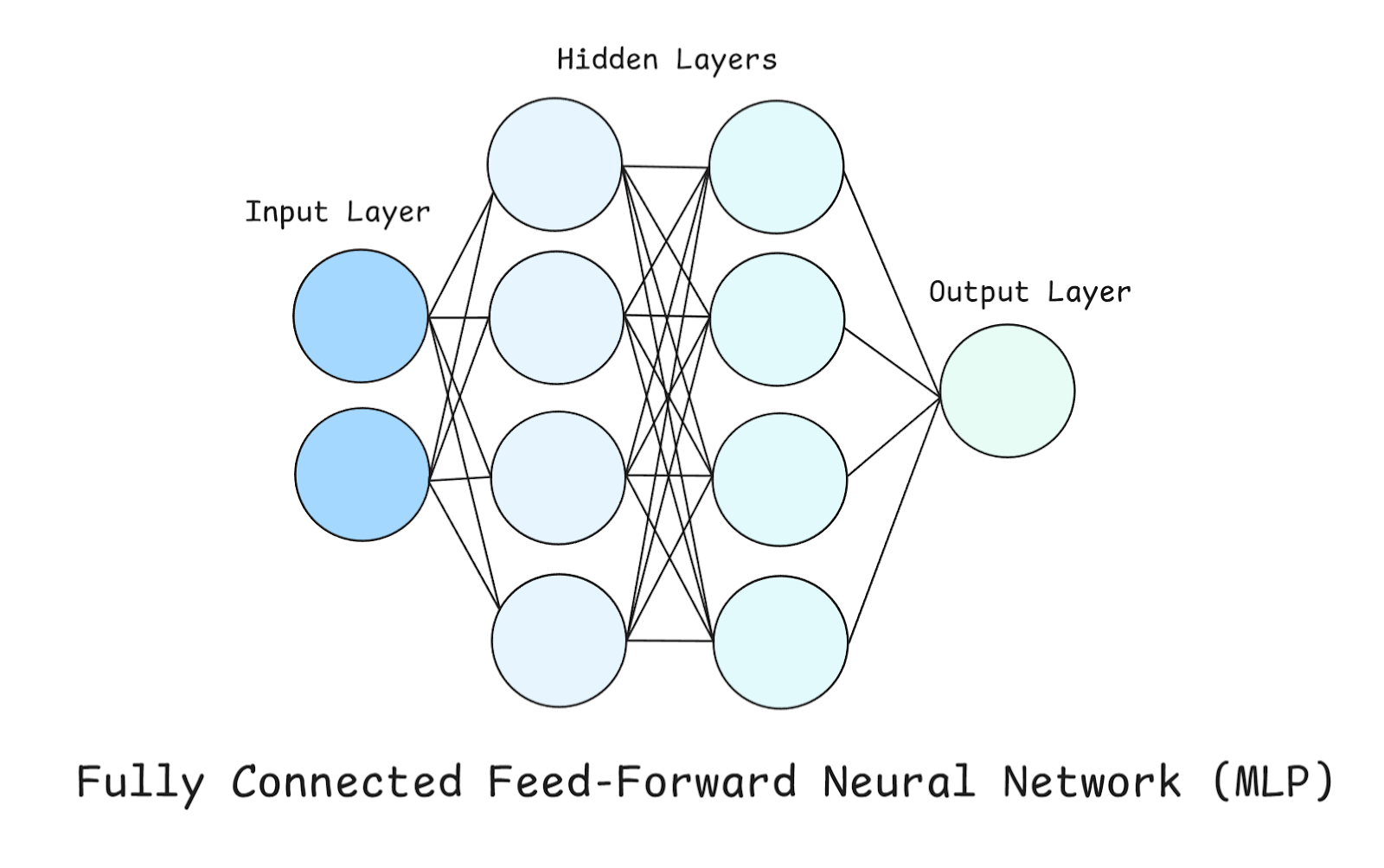
Schau dir das obige Diagramm an, während wir diese Schichten genauer anschauen. 

Eingabeschicht

Das ist der Einstiegspunkt ins Netzwerk.  Jedes Neuron hier steht für ein Merkmal aus dem Datensatz. Wichtig ist, dass die Eingabeschicht keine Berechnungen selbstmacht – sie gibt einfach die Rohdaten weiter. In unserem Beispiel gibt's nur zwei Neuronen in der Eingabeschicht, was heißt, dass unser Datensatz zwei Merkmale hat (oder wir nur zwei Merkmale aus unserem Datensatz berücksichtigen). 

Versteckte Ebenen

Diese sind der Ort, an dem die eigentliche Berechnung stattfindet. Wir haben zwei versteckte Schichten, die jeweils vier Neuronen haben. Jedes Neuron in einer versteckten Schicht macht diese drei Sachen:

1. Gewichtete Summe: Jeder Input wird mit einem Gewicht multipliziert und dann werden alle zusammengezählt. 
2. Voreingenommenheit: Es wird ein konstanter Bias hinzugefügt, um Flexibilität beim Verschieben der Funktion zu ermöglichen.
3. Aktivierungsfunktion: Es wird eine nichtlineare Quetschfunktion wie ReLU, tanh oder Sigmoid benutzt. Dieser Schritt ist wichtig, damit das Netzwerkkomplexe, nichtlineare Muster lernen kann .

Ausgabeschicht

Die Ausgabeschicht macht die endgültige Vorhersage, und wie sie aufgebaut ist, hängt davon ab, welches Problem wir lösen wollen:

• Regressionsprobleme Probleme, wie zum Beispiel die Vorhersage von Immobilienpreisen. In diesem Fall hat die Ausgabeschicht ein Neuron ohne Aktivierung (linear). Warum linear? Weil wir Werte nicht verzerren wollen, können Immobilienpreise jede beliebige reelle Zahl sein.
• Binäre Klassifizierung Probleme (Ja/Nein-Entscheidungen), wie zum Beispiel die Vorhersage, ob eine E-Mail Spam ist oder nicht. Hier wäre die Ausgabeschicht ein Neuron mit einer Sigmoid-Aktivierung. Warum Sigmoid? Das liegt daran, dass wir wollen, dass unser Netzwerk Werte zwischen 0 und 1 ausgibt (weil wir Wahrscheinlichkeiten vorhersagen). 
• Mehrklassenklassifizierung (3 oder mehr Klassen) – wie zum Beispiel die Klassifizierung eines Bildes als verschiedene Tiere. Die Ausgabeschicht hätte ein Neuron pro Klasse mit Softmax-Aktivierungs. Warum Softmax? Weil es die Rohwerte in Wahrscheinlichkeiten umwandelt, die zusammen 1 ergeben (z. B. 70 % Katze, 20 % Hund, 10 % Pferd).

Hier ist ein Diagramm mit neun gängigen Aktivierungsfunktionen, die in FFNN und Deep Learning allgemein verwendet werden. 

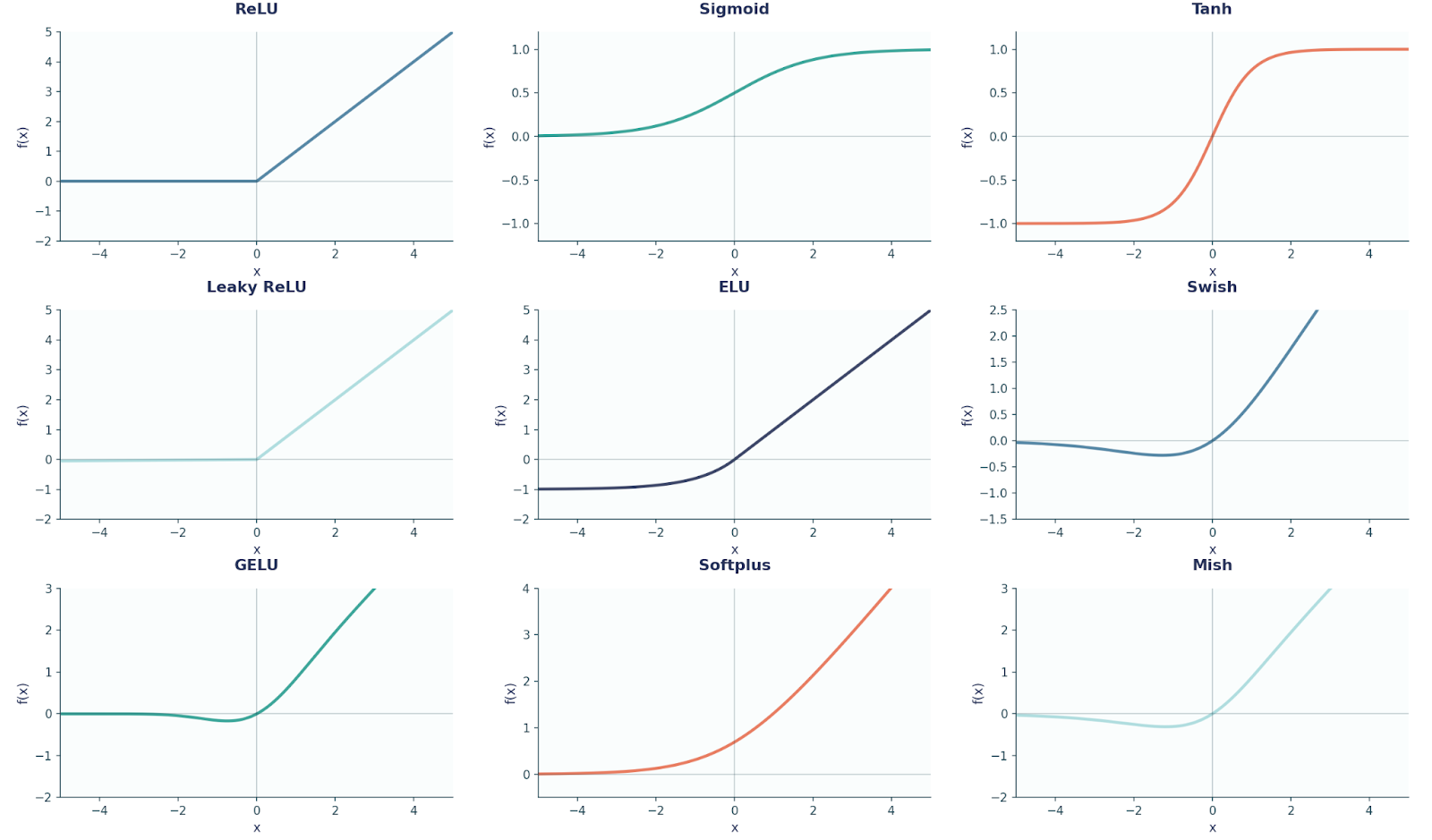
Bevor wir weitermachen, ist es auch wichtig, hier zu erwähnen, dass jede Nervenzelle in einer Schicht mit jedes Neuron in der nächsten Schicht (deshalb spricht man von einer vollständig verbundenen Schicht).

Wenn wir nochmal zu unserem Beispiel zurückkommen, haben wir:

Params = (2⋅4+4)+(4⋅4+4)+(4⋅1+1)=12+20+5=37

Jede Klammer zeigt die Anzahl der Parameter zwischen aufeinanderfolgenden Schichten an, wobei die Anzahl der Neuronen der vorherigen Schicht und der aktuellen Schicht miteinander multipliziert und dann die Anzahl der Biases (d. h. die Anzahl der Neuronen in der aktuellen Schicht) hinzugefügt wird. Probier mal, diese Berechnungen auch an anderen Beispielen für neuronale Netze durchzuführen, um zu üben!

Ein Feedforward-Neuralnetzwerk trainieren

Beim Deep Learning wird das Training in zwei Schritte aufgeteilt: Vorwärtsausbreitung und Rückwärtsausbreitung. Einfach gesagt, gibt uns die Vorwärtspropagation Vorhersagen, während die Rückwärtspropagation zeigt, wie wir aus Fehlern lernen.

Vorwärtsausbreitung 

Alles, was wir bisher besprochen haben, ist Teil der Vorwärtsausbreitung. Zusammengefasst: Wenn Daten durch ein MLP laufen, macht jede Schicht die gleichen zwei Schritte, die man mathematisch mit diesen Gleichungen ausdrücken kann:

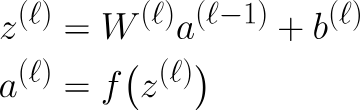
Hier z die Ausgabe, nachdem die Ausgabe der vorherigen Schicht mit den Gewichten der aktuellen Schicht multipliziert und die Vorspannung addiert wurde, auch bekannt als Linear Step.

Wenn die vorherige Schicht die Eingabeschicht ist, dann wäre das natürlich x statt al-1. Der nächste Schritt ist dieAktivierung von „ “ unter. Um das mathematisch genauer zu machen, können wir die Gewichte und die Verzerrung so schreiben:

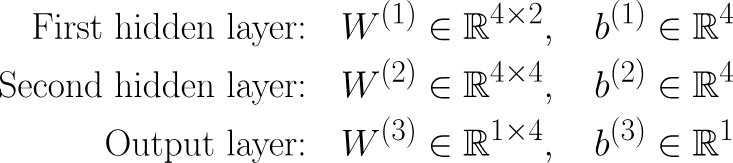
Rückwärtspropagierung

Wenn wir eine Ausgabe bekommen haben, wie sagen wir unserem Netzwerk, ob sie richtig ist oder nicht? Oder besser gesagt: Wie können wir das Netzwerk für unsere Aufgabe besser machen? Hier kommt die Backpropagation ins Spiel. Wir können uns das wie ein Feedback-System für das Netzwerk vorstellen, das dem Modell sagt, wie weit es daneben lag und wie es sich anpassen muss. Wir können das so aufschlüsseln:

1. Vergleiche die Vorhersagen: Schau dir an, was das Modell vorhergesagt hat (ŷ) und was die richtige Antwort war (y).
2. Berechne den Fehler: Wir benutzen eine Verlustfunktion, um zu messen,wie falsch die Vorhersage war, wie zum Beispiel MSE.
3. Verbreite die Rückwärtsausbreitung (über die Kettenregel): Die Gradienten in Bezug auf alle Vorspannungen und Gewichte werden berechnet. ∂L/∂w,∂L/∂b .
4. Gradientenabstieg-Update-: Die entsprechenden Parameter werden nach der folgenden Regel aktualisiert, um Verluste zu reduzieren:

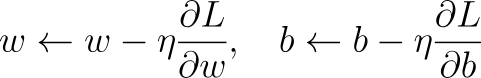
Hier, η die Lernrate, ein Parameter, den man anpassen kann, um festzulegen, um wie viel sich die Parameter bei jeder Aktualisierung ändern sollen.

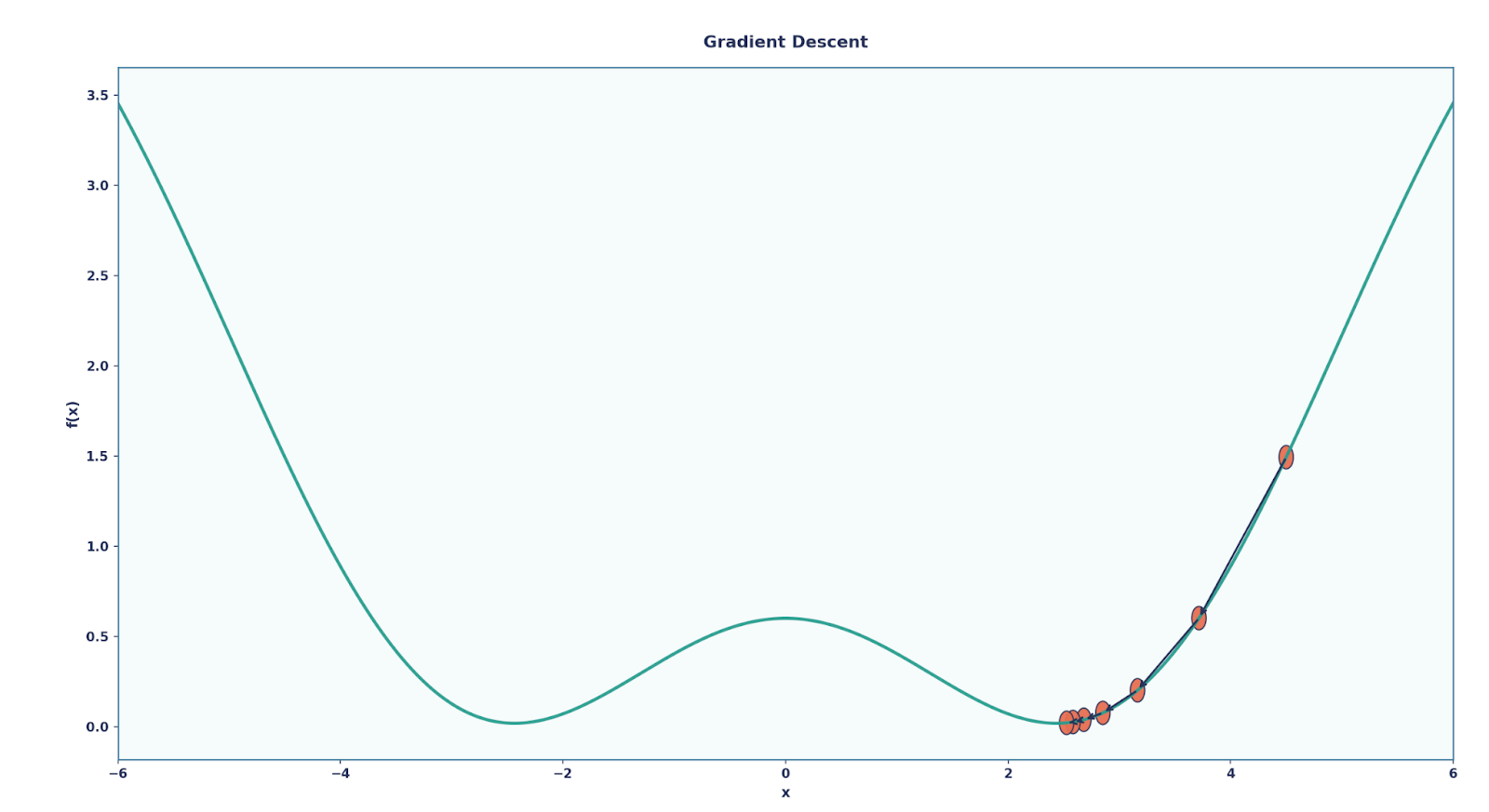
Durch viele Runden dieses Prozesses lernt das Netzwerk nach und nach dazu und wird bei der Aufgabe immer besser.

Um das Ganze zu verdeutlichen, schauen wir uns mal ein kleines Beispiel an. Angenommen, wir haben:

• Eingabe: x = 2
• Zielausgabe: y=4
• Vorhersage: ŷ = 3

Jetzt schauen wir uns die Schritte an. 

1. Vergleiche die Vorhersage: ŷ =3, y = 4
2. Fehler: Für dieses Beispiel nehmen wir den MSE: L = (y − y^​)2=(4−3)2=1
3. Rückwärtspropagieren: Das Netzwerk findet raus, wie viel jedes Gewicht und jede Verzerrung zu diesem Fehler beigetragen hat, indem es Ableitungen nutzt. Dann aktualisieren wir jeden Parameter mit dem Gradientenabstiegsverfahren. 

Ein Feedforward-Neuralnetzwerk in PyTorch programmieren

Wir haben die Mathe-Sachen durchgenommen, die man braucht, um ein FFNN (genauer gesagt ein MLP) zu bauen. Um weiterzukommen, programmieren wir das jetzt in PyTorchprogrammieren.

Mehrschichtiges Perzeptron

# Imports we will be needing
import torch
import torch.nn as nn
import torch.optim as optim

X,y = dataset # Here will be our dataset 

# We have created a MLP here using nn.Sequential()
model = nn.Sequential(
    nn.Linear(2, 4),  # input layer → hidden layer (2 → 4)
    nn.ReLU(),        # relu activation function
    nn.Linear(4, 4), # hidden layer 1 → hidden layer 2 (4 → 4)
    nn.ReLU(), 
    nn.Linear(4, 1)   # hidden layer 2 → output (4 → 1)
)


criterion = nn.MSELoss()         # regression loss, i.e our loss function
optimizer = optim.SGD(model.parameters(), lr=0.1) # Optimizer using the Stochastic Gradient Descent

# Training Loop
EPOCHS = 200 # Number of epochs we will be training for
for epoch in range(EPOCHS):
    # Forward pass
    outputs = model(X)
    loss = criterion(outputs, y)

    # Backward pass
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

Jetzt solltest du den PyTorch-Code den mathematischen Schritten zuordnen können, die wir vorher besprochen haben. Du hast vielleicht eine Frage zu Epochen.

Ein Epochen- us ist ein kompletter Durchlauf des gesamten Trainingsdatensatzes durch das neuronale Netzwerk. Nehmen wir mal an, wir haben 1.000 Trainingsdatenpunkte und eine Batchgröße von 100. Wenn das Netzwerk dann alle 1.000 Bilder (also 10 Batches) gesehen hat, ist das eine Epoche. Das Training braucht normalerweise viele Epochen, , damit das Modell seine Gewichte immer weiter verbessern kann.

Faltungsneuronales Netzwerk

Ich möchte auch kurz auf andere FFNNs eingehen, von denen eines sehr bekannt ist: das Convolutional Neural Network (CNN).

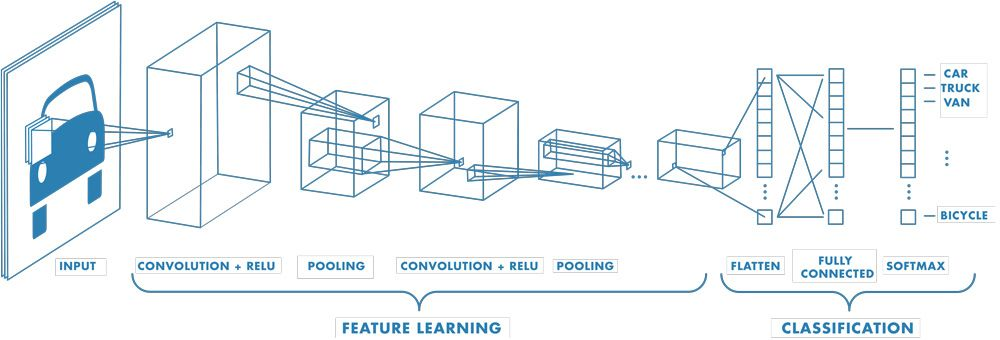
Ein CNN hat zwar am Ende auch ein MLP, aber am Anfang hat es diese speziellen Schichten, die man Convolutional Layers und Pooling Layers nennt. Zuerst mal zu den Convolutional Layers: Die sind echt wichtig, weil sie mit einemFilter (oder Kernel)namens „ ” immer nur kleine Bereiche der Eingabe auf einmal anschauen.

Das ist echt praktisch, wenn man Bilder sortiert, weil:

• Dichte Schichten hätten jedes Pixel als eigenständig behandelt und die räumliche Struktur nicht beachtet.
• Faltungs-Schichten können dagegen Kanten, Texturen und Formen in kleinen Bereichen erkennen – und diese dann zu komplexeren Mustern zusammenfügen, je tiefer wir gehen.

Neben Faltungsschichten nutzen CNNs auch Pooling-Schichten.

Es ist wichtig zu wissen, dass Pooling-Schichten keine Parameter lernen, sondern die Feature-Maps verkleinern die Merkmalkarten herunter, um sie kleiner und überschaubarer zu machen.

• Das häufigste ist Max Pooling, bei dem man den höchsten Wert aus jedem kleinen Bereich (z. B. einem 2×2-Fenster) nimmt.
• Pooling macht das Netzwerk effizienter und sorgt auch für Übersetzungsinvarianz (das Netzwerk kümmert sich mehr darum, ob ein Merkmal vorhanden ist, als darum, wo genau es sich befindet).

Wir können ein CNN mit PyTorch so programmieren:

class SimpleCNN(nn.Module): # Define our model as a class
    def __init__(self):
        super().__init__()
        self.conv = nn.Conv2d(1, 8, 3)     # 1→8 channels, 3x3 kernel
        self.pool = nn.MaxPool2d(2, 2)
        self.fc   = nn.Linear(8*13*13, 10) # flatten → 10 classes

    def forward(self, x): # Forward propagation function 
        x = self.pool(torch.relu(self.conv(x)))
        x = x.view(x.size(0), -1)          # flatten
        return self.fc(x)

Im obigen Code haben wir ein ganz einfaches CNN erstellt, das aus einer einzigen Faltungsschicht, einer einzigen Pooling-Schicht und einer einzigen linearen Schicht besteht. 

Weitere Beispiele für Feedforward-Neuralnetzwerke

Wir haben zwei echt bekannte und wichtige Beispiele für FFNNs angeschaut, aber es gibt noch viele andere, die in ihren jeweiligen Bereichen echt revolutionär waren, wie zum Beispiel:

1. Transformers: Jeder Block hat einen MLP/FFN-Teil (nach der Selbstaufmerksamkeit erweitert und verkleinert die „Feed-Forward-Schicht” die Dimensionen).
2. Vision Transformers (ViTs): verwenden Transformer-Blöcke (mit FFNNs darin) für Bildausschnitte.
3. Autoencoder (grundlegende): Encoder + Decoder sind beide aus FFNNs gemacht.
4. Empfehlungssysteme (MLP-basiert): z. B. Wide & Deep-Modelle für Rankings und Vorhersagen.

Abschließende Gedanken

Ich hoffe, du hast erkannt, wie wichtig FFNNs im Bereich der KI sind. Ohne diese Dinge gäbe es die moderne Welt des Deep Learning nicht.

Um weiterzumachen, würde ich echt empfehlen, Backpropagation zu meistern und dich mehr mit Aktivierungsfunktioneneinzuarbeiten. Da das die Grundlage für Deep Learning ist, würde ich auch empfehlen, Deep Learning mit PyTorch.