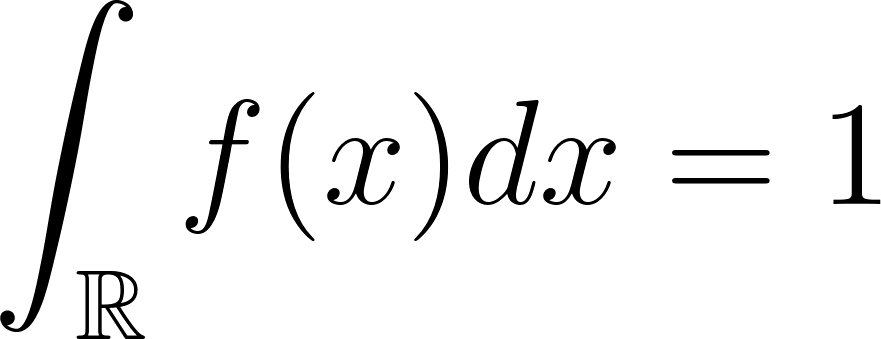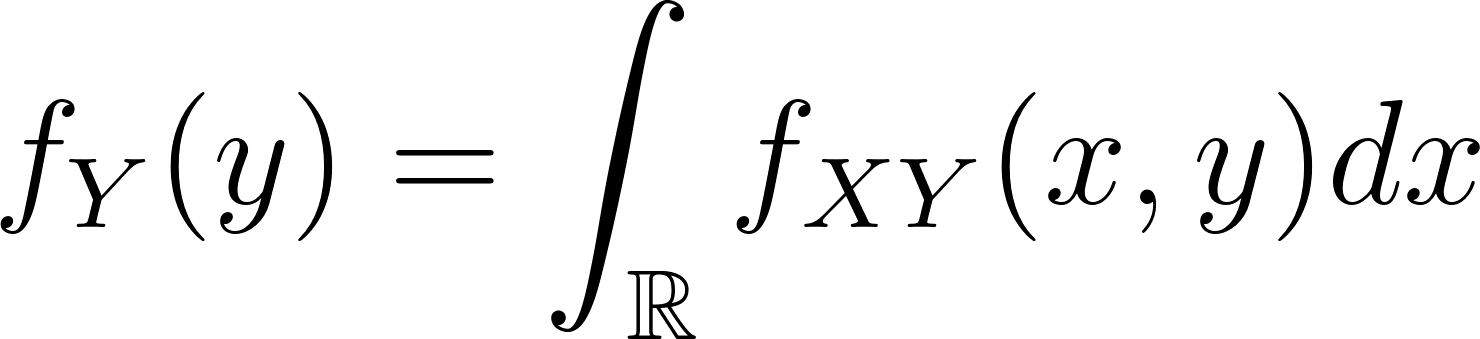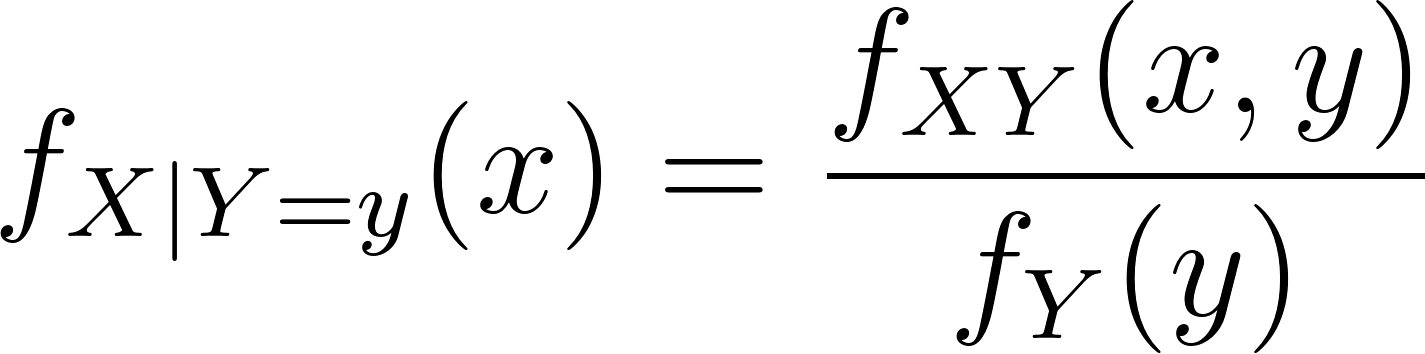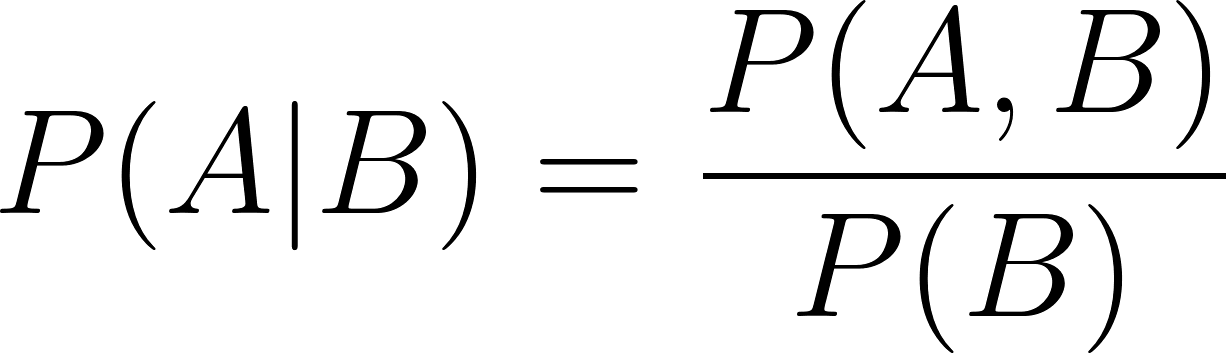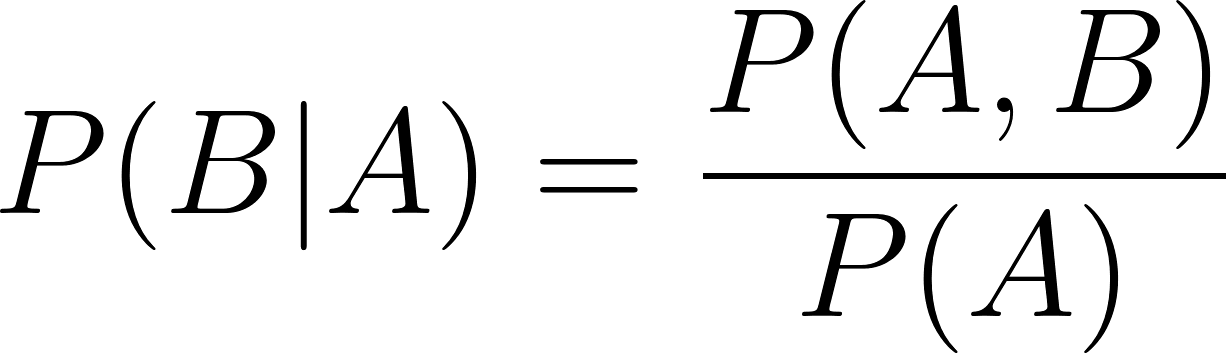Curso
Los modelos de aprendizaje automático (AM) son implementaciones informáticas de métodos estadísticos y probabilísticos. Generalmente adoptan uno de estos dos enfoques: modelado generativo o discriminativo.
En este artículo, ofrecemos una visión general de los modelos generativos y discriminativos, presentamos modelos comunes de cada tipo, explicamos los principios matemáticos en los que se basan ambos enfoques y analizamos ejemplos prácticos de los tipos de problemas para los que se puede utilizar cada tipo de modelo.
¿Qué son los modelos generativos?
Dado un conjunto de puntos de datos de ejemplo, D, y sus etiquetas asociadas, L, un modelo generativo aprende la distribución de probabilidad conjunta P(D, L). A continuación, utiliza esta distribución subyacente para generar nuevos datos similares a los ejemplos de entrenamiento o abordar problemas de clasificación.
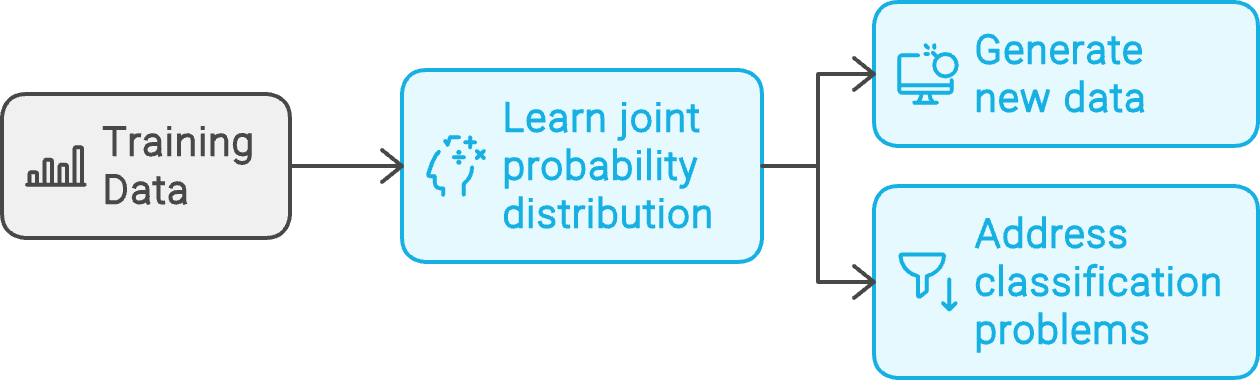
Flujo de trabajo del modelo generativo. Creado con napkin.ai
Las secciones siguientes explican los fundamentos de los modelos generativos con ejemplos.
Modelos Naive Bayes
Los modelos Naive Bayes se basan en el teorema de Bayes. Este teorema da la probabilidad condicional P(A | B) de un suceso A cuando se sabe que el suceso B es cierto. Se denomina probabilidad posterior de A dado B.
Individualmente, la probabilidad P(A) del suceso A se denomina probabilidad a priori. Los modelos Bayes ingenuos suponen que A y B son sucesos independientes, de ahí el prefijo "ingenuo". Si A y B son dependientes, el teorema de Bayes tradicional ya no se aplica, y los modelos Naive Bayes no son la elección correcta.
Los modelos bayesianos son modelos generativos porque modelizan la distribución de probabilidad conjunta. El proceso de entrenamiento aprende la probabilidad conjunta- P(A, B). Tras el entrenamiento, puede utilizarse para predecir los valores de A con la mayor probabilidad P(A). Además, los modelos bayesianos también pueden utilizarse para la clasificación, porque pueden calcular probabilidades condicionales (utilizando la regla de Bayes).
Para aprender a utilizar modelos Naive Bayes en la práctica, sigue el tutorial sobre la construcción de modelos Naive Bayes utilizando scikit-learn y Python.
Modelos de mezcla gaussiana
Los modelos gaussianos de mezclas (GMM) son una clase de modelos de mezclas. Su premisa única es que los datos subyacentes combinan distribuciones estadísticas en lugar de una única distribución.
En un MMG, se supone que la población es una combinación de distintas subpoblaciones, cada una de las cuales es una distribución gaussiana. En efecto, la distribución de los datos se analiza como una media ponderada de unas cuantas distribuciones gaussianas individuales.
Los MMG captan la distribución de probabilidad del conjunto de datos subyacente. Así, se utilizan para tareas como el análisis de valores atípicos y la clasificación no supervisada. Estas tareas implican construir un modelo estadístico de la población tratando el conjunto de datos de entrenamiento como una muestra aleatoria.
El curso sobre modelos de mezcla en R entra en los detalles prácticos de los MMG.
Redes Generativas Adversariales
Una red generativa adversarial (GAN) es un modelo basado en redes neuronales. Consta de dos partes: un generador y un discriminador. La red generadora se entrena para generar vectores similares a los ejemplos de entrenamiento, mientras que el discriminador se entrena para distinguir entre los ejemplos originales y los generados por el generador.
En esencia, el generador y el discriminador tienen objetivos de entrenamiento opuestos, lo que los convierte en adversarios. De ahí que se utilice la palabra "adversarial" en el nombre.
El generador y el discriminador se entrenan juntos en el mismo bucle de entrenamiento. A medida que el generador mejora en la creación de ejemplos realistas, el discriminador distingue los ejemplos originales de los generados. El entrenamiento continúa hasta que el generador aprende a generar ejemplos tan parecidos a los datos de entrenamiento que el discriminador no puede distinguirlos.
Tras el entrenamiento, el generador se utiliza para generar datos sintéticos realistas similares a los ejemplos originales.
Modelos de Markov ocultos
Un modelo de Markov oculto (HMM) funciona con conjuntos de datos secuenciales. Los procesos de Markov (o cadenas de Markov) se utilizan para modelar datos secuenciales. La premisa de un modelo de Markov es que el siguiente elemento, xn+1de la secuencia sólo depende del elemento anterior, xny no de ninguno de los elementos, {x1, x2, ... xn-1}antes de ella. Los modelos de Markov suponen que los conjuntos de datos secuenciales pueden representarse mediante procesos de Markov con estados ocultos.
Estos estados generan el siguiente elemento de la secuencia:
- La salida actual del modelo depende sólo del estado actual
- El estado actual sólo depende del estado anterior. La premisa de los modelos de Markov es que toda la información relevante desde el estado inicial hasta el (N-2)º estado está encapsulada en el (N-1)º estado. No es necesario considerar explícitamente los estados anteriores.
Los modelos de Markov se representan con probabilidades de transición (pasar de un estado a otro) y probabilidades de emisión (generar un determinado elemento de la secuencia dado un determinado estado).
Los HMM modelan los conjuntos de datos de entrenamiento como procesos de Markov. El objetivo del entrenamiento es determinar las probabilidades de transición y emisión para maximizar la probabilidad de generar las secuencias de los conjuntos de datos de ejemplo. Así, dada una secuencia, un modelo de Markov entrenado puede generar los elementos sucesivos de la secuencia.
Para conocer su aplicación práctica, sigue el tutorial sobre cadenas de Markov en Python.
¿Qué son los modelos discriminatorios?
Dado un conjunto de datos de entrenamiento formado por puntos de datos, D, y sus etiquetas asociadas, L, un modelo discriminativo aprende la distribución de probabilidad condicional P(D | L). A continuación, utiliza esta distribución de probabilidad condicional para predecir la clase de los nuevos puntos de datos.

Flujo de trabajo del modelo discriminatorio. Creado con napkin.ai
Los modelos discriminatorios se utilizan generalmente para resolver problemas de clasificación. Los siguientes ejemplos demuestran sus casos de uso.
K-vecinos más cercanos
K-vecinos más cercanos (KNN) es uno de los modelos de aprendizaje automático más antiguos. Se basa en la premisa de que, dada una distribución de puntos de datos, los elementos similares se sitúan en proximidad.
Los modelos KNN son no paramétricos, sin parámetros como los coeficientes de regresión. Se utilizan tanto para problemas de clasificación como de regresión.
La categoría de un punto de datos de entrada es la misma que la de sus k vecinos más próximos. El valor predicho de un punto de datos es el valor medio de sus k vecinos más próximos. k (el número de vecinos más próximos a considerar) puede considerarse un hiperparámetro del modelo. Se utiliza para ajustar el comportamiento del modelo, pero no afecta directamente a su resultado.
Regresión logística
La regresión logística, al igual que la regresión lineal, intenta predecir el valor de una variable dependiente en función de una o varias variables independientes. En la regresión lineal, la variable dependiente toma valores continuos. En la regresión logística, la variable dependiente toma valores discretos, como por ejemplo
- Verdadero y falso (regresión logística binaria)
- Una lista de categorías (regresión logística multinomial)
- Una lista de valores ordenados, como un sistema de calificación basado en letras: A, B, C, D, E, F (regresión logística ordinal)
La regresión lineal predice valores numéricos. En la regresión logística, la cantidad predicha es el logaritmo de la odds ratio.
Para un acontecimiento Acon probabilidad P(A)la razón de probabilidades es P(A) / (1 - P(A)). Utilizar el logaritmo (de la razón de probabilidades) conduce a una convergencia más suave y rápida durante el proceso de entrenamiento. Dada su capacidad para segregar entradas en clases, los modelos logísticos se utilizan con fines discriminativos.
Para una introducción más práctica a este tema, consulta la guía sobre regresión logística en Python.
También puedes implementar la regresión logística utilizando R, un lenguaje de programación orientado a la estadística, como se explica en el tutorial sobre regresión logística utilizando R.
Máquinas de vectores soporte (SVM)
Las máquinas de vectores soporte determinan la línea óptima que separa los puntos de datos de diferentes clases. En el plano bidimensional X-Y, dada una colección de puntos de datos de dos categorías diferentes, la SVM predice una línea que (idealmente) separa limpiamente los puntos de una categoría de los de la otra.
Esta línea es el límite de decisión. Se convierte en un hiperplano para datos con tres o más dimensiones. Los puntos de datos (de cualquiera de las categorías) que se encuentran más cerca de esta línea imaginaria se denominanvectores de apoyo del modelo . Estos puntos de datos son los más difíciles de clasificar, ya que sus valores son próximos.
La distancia entre la línea de separación y los vectores soporte se denomina margen. El objetivo del entrenamiento SVM es encontrar el límite de decisión que maximice este margen. En la práctica, los puntos de datos tienen más de dos dimensiones, y la línea de separación es un hiperplano de mayor dimensión.
Las SVM también se utilizan para problemas de clasificación multiclase.
Para saber más sobre las SVM, sigue esta guía sobre la construcción de SVM utilizando el paquete scikit-learn de Python. Además de Python, también puedes utilizar R para implementar SVMs, como se explica en esta guía sobre SVMs en R.
Árboles de decisión y bosques aleatorios
Un árbol de decisión consta de varios nodos de decisión organizados en una estructura arborescente.
El nodo superior es la raíz. Los nodos que conducen a las salidas finales se llaman nodos hoja o nodos terminales. Los nodos intermedios no hoja se llaman nodos internos. La salida del nodo raíz alimenta a los nodos intermedios. El resultado (salida) de cada nodo es la salida final o conduce (ramifica) a otro nodo.
Cada nodo del árbol divide el conjunto de datos según un atributo concreto. Por ejemplo, un árbol de decisión para aprobar solicitudes de préstamo podría tener nodos para segregar las solicitudes según sus ingresos netos.
El proceso de entrenamiento determina el valor umbral adecuado para cada decisión. Por ejemplo, las solicitudes con ingresos netos inferiores a una determinada cantidad son rechazadas de plano. El resto se procesa en nodos posteriores, que tienen en cuenta otros atributos, como la riqueza neta.
Para una guía práctica sobre los árboles de decisión, sigue el tutorial sobre la construcción de árboles de decisión utilizando Python, o el curso completo sobre aprendizaje automático con modelos basados en árboles en Python.
El principal inconveniente de los árboles de decisión es el sobreajuste, que provoca problemas de datos fuera de muestra. Los bosques de decisión intentan resolver este problema. Un bosque de decisiones está formado por muchos árboles. A diferencia de los árboles de decisión independientes, que deben considerar todo el conjunto de características, cada árbol de un bosque sólo encuentra un subconjunto aleatorio del conjunto de características. Esta aleatoriedad ayuda a hacer frente a la varianza de los conjuntos de datos ruidosos.
La salida del bosque se obtiene combinando, por ejemplo, promediando, la salida de los árboles individuales.
Para aprender a implementar los bosques aleatorios, consulta la guía sobre el uso de scikit-learn para construir clasificadores de bosques aleatorios.
Redes neuronales
Una red neuronal está formada por grupos de neuronas. Cada neurona implementa una función lineal que multiplica los pesos de la neurona por el vector de entrada.
Una función de activación no lineal sigue a la función lineal. La función de activación decide la salida de cada neurona basándose en la salida de la función lineal. Así, una red neuronal simple puede verse conceptualmente como una serie de ecuaciones lineales filtradas por activaciones no lineales.
La capa de entrada de una red neuronal multiplica la entrada (representada como un vector) por un conjunto de pesos y funciones de activación. Esta salida se pasa a la capa siguiente, que realiza una operación similar.
Las capas ocultas están entre las capas de entrada y salida . La última capa oculta alimenta la capa de salida. Los problemas complejos implican utilizar redesneuronales con muchas capas ocultas, que se denominan redes neuronales profundas (DNN).
En un problema de clasificación, un enfoque habitual es tener tantas neuronas de salida como clases haya. La clase predicha corresponde a la neurona con el valor más alto. En un problema de regresión, una sola neurona de salida contiene la salida prevista. Las relaciones lineales de las neuronas modelan la ecuación de regresión lineal.
Para profundizar en el tema, consulta la entrada del blog sobre redes neuronales.
Diferencias entre los modelos Generativo y Discriminativo
Algunas tareas, como la clasificación, pueden resolverse utilizando cualquiera de los dos tipos de modelos. En general, sin embargo, los modelos discriminativos y generativos suelen tener casos de uso únicos, ya que estos modelos adoptan enfoques matemáticos diferentes. Es necesario comprender estas diferencias y cómo afectan a la adecuación de una u otra categoría de modelos a diversos problemas.
Enfoque del modelado
Los modelos generativos predicen el siguiente valor de una secuencia o generan una imagen a partir de un texto (o viceversa). Para realizar estas tareas, el modelo tiene que aprender qué salida generar dadas distintas entradas. El modelo utiliza ladistribución de probabilidad conjunta de la entrada y la salida .
Para entender las matemáticas subyacentes, empecemos con un ejemplo sencillo. El comportamiento de una única variable aleatoria se describe mediante sufunción de densidad de probabilidad (PDF) .
La PDF de la variable aleatoria X puede utilizarse para determinar la probabilidad de X en distintos valores. Por ejemplo, si la PDF de X es f(x)la probabilidad de que X se encuentre entre A y B viene dada por :
La probabilidad de X en todo el intervalo es 1. Esto se expresa como :
La expresión anterior también puede escribirse como
Para una PDF conjunta de dos variables, X y Yla integral sobre todo el intervalo es 1:
La distribución de probabilidad conjunta cartografía todo el espacio de probabilidad de X e Y. Para evaluar la probabilidad de que la probabilidad conjunta P(X, Y) caiga en una región G, integra la PDF conjunta sobre G:
Los modelos discriminatorios, en cambio, se centran sólo en la distribución de probabilidad condicional. Los modelos generativos, si son necesarios, estiman la probabilidad condicional utilizando las probabilidades marginales.
Dada una distribución de probabilidad conjunta fXY(x,y)la probabilidad marginal de la variable aleatoria Y en el valor y (para todos los valores de X) viene dado como
De forma similar a la regla de Bayes, la PDF condicional de X se expresa entonces como
La expresión anterior muestra la versión integral de la probabilidad condicional, que se escribe más comúnmente como:
Del mismo modo,
En las dos fórmulas de probabilidad condicional anteriores:
- El lado izquierdo (LHS) es la probabilidad condicional (los condicionales)
- El numerador del lado derecho (RHS) es la probabilidad conjunta
- El denominador del lado derecho es la probabilidad marginal.
Para calcular una probabilidad condicional, los modelos generativos siguen dos pasos:
- Estimación de la PDF conjunta y de los marginales.
- Evalúa la expresión de la parte derecha de la ecuación anterior.
En cambio, los modelos discriminativos siguen un único (y más sencillo) paso:
- Estima directamente la probabilidad condicional (el lado izquierdo de la ecuación) basándote en los datos de entrenamiento.
Flexibilidad y complejidad
Un modelo generativo tiene los marginales P(A) y P(B) y la PDF conjunta P(A, B). Utilizándolos, puede evaluar P(A | B) o P(B | A) con la misma facilidad. Ésta es la idea subyacente a los clasificadores Bayes ingenuos. Así, los modelos generativos pueden realizar tareas como:
- Generar nuevos ejemplos utilizando la distribución de probabilidad conjunta.
- Predecir la etiqueta más relevante dado un nuevo ejemplo utilizando la probabilidad condicional.
- Predecir el ejemplo más relevante dada una nueva etiqueta utilizando la otra probabilidad condicional.
- Estimar la probabilidad global de determinados sucesos utilizando las probabilidades marginales.
Esto hace que los modelos generativos sean flexibles y polivalentes. Por otra parte, implican intrínsecamente una mayor complejidad durante el entrenamiento porque:
- El modelo necesita estimar las FDP conjuntas y las FDP marginales
- A continuación, si es necesario, el modelo evalúa las condicionales
Los modelos discriminativos, en cambio, sólo se ocupan de los condicionales. A partir del conjunto de datos de entrenamiento, es posible estimar directamente las probabilidades condicionales sin estimar las probabilidades conjuntas o marginales.
Así, los modelos discriminativos son más sencillos de entrenar. Sin embargo, un modelo discriminativo que ha aprendido la probabilidad condicional P(A | B) sólo puede realizar tareas que impliquen esta probabilidad condicional concreta. No puede hacer otra cosa.
Rendimiento en tareas de clasificación
Los modelos generativos son lo suficientemente flexibles para tareas tanto generativas como discriminativas. Durante el entrenamiento, el modelo aprende la PDF conjunta y los marginales. Durante la inferencia, el modelo debe calcular la probabilidad condicional utilizando la distribución conjunta y la probabilidad marginal adecuada. Por lo tanto, la inferencia en tareas discriminativas es más lenta.
Los modelos discriminativos, en cambio, han aprendido directamente (numéricamente) las probabilidades condicionales. Estiman la probabilidad condicional en un solo paso basándose en los datos de entrada durante la inferencia.
Además, como los modelos discriminativos sólo se centran en estimar una única cantidad (la probabilidad condicional), se observa que son más precisos. Una PDF conjunta tiene más incertidumbre incorporada que una simple probabilidad condicional. Esta incertidumbre añadida se refleja en la precisión relativamente menor de los modelos generativos para las tareas de clasificación.
Modelos Generativos vs Discriminativos: Un resumen
Basándonos en la discusión de las secciones anteriores, la tabla siguiente resume las diferencias entre los modelos generativos y los discriminativos.
|
Modelos generativos |
Modelos discriminatorios |
|
|
Objetivo |
Captura la probabilidad conjunta y la probabilidad marginal. Utiliza la regla de Bayes para calcular la probabilidad condicional. |
Captura sólo la probabilidad condicional. No hay información sobre las probabilidades conjuntas o marginales. |
|
Generación de datos |
Puede generar nuevos puntos de datos basándose en el conjunto de datos de entrenamiento. Por ejemplo, un modelo entrenado con dígitos manuscritos puede generar dígitos nuevos y falsos. |
No se pueden generar nuevos puntos de datos. Se centra principalmente en distinguir entre distintas categorías de datos. |
|
Caso de uso principal |
Puede utilizarse tanto para tareas generativas (por ejemplo, síntesis de datos) como para tareas discriminativas (por ejemplo, clasificación). |
Sólo puede utilizarse para tareas discriminativas como la clasificación o la regresión. |
|
Rendimiento de la inferencia |
Ejecutar la inferencia es más lento debido a la necesidad de realizar cálculos complejos. Incluso las tareas más sencillas requieren calcular probabilidades marginales y conjuntas y aplicar la regla de Bayes. |
Inferencia más rápida porque calcula directamente la probabilidad condicional sin implicar la regla de Bayes. |
|
Tratamiento de los datos que faltan |
Maneja mejor los datos que faltan modelando la distribución de probabilidad subyacente, lo que facilita "rellenar los huecos". Menor riesgo de sobreajuste. |
Menos eficaz a la hora de tratar los datos que faltan. Mayor riesgo de sobreajuste porque el modelo se centra en encontrar el hiperplano de separación entre clases. |
|
Convergencia |
Suelen converger más rápido y con menos ejemplos de entrenamiento, pero suelen dar lugar a un error de modelo más elevado, sobre todo en tareas de clasificación, debido al cálculo indirecto de la probabilidad condicional mediante el modelado de la distribución de probabilidad conjunta. |
Generalmente requieren más datos para entrenarse y pueden converger más lentamente. Sin embargo, el resultado es un menor error del modelo, especialmente en tareas de clasificación, porque modelan directamente la probabilidad condicional sin estimar la distribución de probabilidad conjunta. |
|
Complejidad del modelo |
Suelen ser más complejas porque modelan toda la distribución de datos, incluidas las interacciones entre características y etiquetas. |
Generalmente son más sencillos porque sólo necesitan modelar el límite de decisión o hiperplano separado entre clases. |
|
Ejemplos de modelos |
Bayas ingenuas, modelos ocultos de Markov (HMM), redes generativas adversariales (GAN), autocodificadores variacionales (VAE). |
Regresión logística, máquinas de vectores de apoyo (SVM), redes neuronales y árboles de decisión. |
|
Modelo de flexibilidad |
Más flexible en términos de aplicación (puede manejar tanto tareas generativas como discriminativas). |
Menos flexible (limitado a tareas discriminativas). |
|
Tasas de error |
Mayores tasas de error en las tareas de clasificación debido a los métodos de estimación indirecta. |
Tasas de error más bajas en tareas de clasificación gracias al entrenamiento directo sobre la probabilidad condicional. |
Cuándo utilizar modelos generativos
Como su nombre indica, los modelos generativos están especialmente indicados para tareas que implican generar nuevos datos que se ajusten a los patrones de los datos de entrenamiento.
Algunos casos de uso común de estos modelos son
1. Generación de datos sintéticos
Para muchos modelos de visión por ordenador, es esencial disponer de un gran conjunto de datos de imágenes de entrenamiento. Estos modelos deben entrenarse con muchas variantes de la misma imagen o característica.
Tomar fotos del mismo objeto desde distintos ángulos, fondos o tonos de color no siempre es realista. Muchos conjuntos de datos de imágenes de tareas específicas también tienden a tener un tamaño limitado porque su creación requiere habilidades específicas del dominio. Por ejemplo, necesitas acceso a neumólogos, laboratorios de radiología y pacientes y hospitales que den su consentimiento para crear un conjunto de imágenes de radiografías de una enfermedad pulmonar concreta.
En tales casos, la opción más pragmática es crear un conjunto de datos pequeño pero muy curado y relevante, y luego generar sintéticamente nuevos puntos de datos similares al conjunto de datos original.
2. Generación de imágenes y textos
Generar nuevas imágenes a partir de una descripción textual o generar un nuevo texto a partir de un texto de entrada. La única clase de modelos que puede encargarse de tales tareas son los modelos generativos.
Los modelos de generación de imágenes como DALL-E, MidJourney y Stable Diffusion se utilizan habitualmente para generar imágenes que se ajusten a una descripción específica y no infrinjan los derechos de autor existentes.
Del mismo modo, los LLM se utilizan a menudo para generar argumentos de historias ficticias, eslóganes y eslóganes de marketing, resúmenes de documentos y otros materiales similares.
3. Modelización de distribuciones de probabilidad conjuntas
Los modelos generativos se utilizan para tareas basadas en la distribución de probabilidad conjunta de los datos subyacentes. Modelizar la distribución conjunta de los rendimientos de los activos para predecir el perfil de riesgo y rendimiento esperado de una cartera de inversión es algo habitual en finanzas y gestión de riesgos.
Por ejemplo, un gestor de inversiones puede querer saber la probabilidad de que los precios de dos acciones diferentes suban o bajen al mismo tiempo: las PDF conjuntas pueden responder a estas preguntas.
El sector de los servicios financieros lleva utilizando estos métodos estadísticos mucho antes de que se adoptara ampliamente el término "modelos generativos".
4. Clasificación no supervisada
Problemas como la clasificación no supervisada son especialmente adecuados para los modelos de mezclas gaussianas. En estos problemas, tienes una amplia colección de puntos de datos, pero no sabes a cuántos ni a qué categorías pertenecen. Es razonable esperar que los datos procedan de una combinación de distribuciones, que un MMG puede modelizar.
Si se hubieran conocido de antemano el número y la lista de categorías, los métodos discriminatorios habrían sido más apropiados.
Los MMG también son útiles en el análisis de valores atípicos (detección de anomalías, detección de fraudes, etc.), donde los datos "habituales", como el comportamiento de distintos grupos de clientes, pueden modelarse como una combinación de distintas distribuciones. Los puntos de datos anómalos son los que difieren significativamente de cualquiera de los otros patrones.
5. Modelado de secuencias
Los problemas que implican secuencias se resuelven a menudo utilizando modelos ocultos de Markov. Un caso de uso cotidiano es el modelado de secuencias genómicas y la resecuenciación.
Los HMM también se utilizan en el reconocimiento del habla, donde ayudan a predecir la siguiente sílaba dada la secuencia de sílabas precedentes. El modelado de secuencias también es habitual en aplicaciones logísticas, como los horarios de entrega de paquetes. Del mismo modo, la transmisión y propagación de enfermedades infecciosas suelen modelarse mediante cadenas de Markov.
Cuándo utilizar modelos discriminatorios
Matemáticamente, los modelos discriminativos se utilizan para aplicaciones en las que sólo es relevante la probabilidad condicional, pero no la probabilidad conjunta. Así, los modelos discriminativos se suelen utilizar para problemas de clasificación y problemas de predicción.
Algunos ejemplos son:
1. Problemas de clasificación supervisada
Problemas de clasificación supervisada, en los que las clases (categorías) se conocen de antemano. Este es el caso de uso por excelencia de los KNN y los SVM.
Dispones de una amplia colección de puntos de datos, como datos sobre el comportamiento de los clientes, incluidos patrones de gasto, importes de compra, frecuencia de compra, historial de devoluciones, etc. Tienes que utilizar esta información para clasificar la lista de clientes en distintas categorías, como los que gastan mucho, los que buscan gangas, los clientes habituales, los que no son serios, etc. Esto contrasta con los problemas de clasificación no supervisada, en los que, como ya se ha dicho, se suelen utilizar los MMG.
2. Tareas predictivas
En tareas predictivas como la clasificación y la regresión, la prioridad suele ser la velocidad y la precisión. En principio, los modelos generativos también son capaces de resolver esos problemas.
En particular, se prefieren los modelos generativos cuando hay problemas como puntos de datos que faltan, cuando sólo se dispone de un conjunto de datos limitado para el entrenamiento, o cuando esperas añadir nuevas categorías de forma rutinaria.
Sin embargo, para la mayoría de los casos de uso estándar, los modelos generativos adolecen de tasas de error más elevadas y de una inferencia más lenta en las tareas predictivas, porque su cálculo implica la distribución de probabilidad conjunta. Por tanto, para los problemas estándar de clasificación y regresión, en los que se dispone de un conjunto de datos grande y sano para el entrenamiento, los modelos discriminativos son la opción preferida debido a sus mejores características de rendimiento.
3. Clasificación centrada en los resultados
Los modelos discriminatorios son preferibles para tareas que se centran sólo en el resultado de la clasificación y no en modelar los datos subyacentes.
Por ejemplo, si quieres clasificar las grabaciones de audio en sus respectivas lenguas, no necesitas un modelo que entienda la lengua y la gramática. Un modelo de reconocimiento de voz sería excesivo para un problema de clasificación. Basta con centrarse en el límite de decisión utilizando un modelo discriminativo. Así, puedes utilizar una simple red neuronal en lugar de un LLM o una regresión logística en lugar de un modelo bayesiano.
4. Toma de decisiones en varios pasos
Las decisiones en varios pasos, en las que los pasos individuales implican elecciones inequívocas, son buenas candidatas para los árboles de decisión. Los árboles de decisión suelen utilizarse como filtro preliminar para preseleccionar puntos de datos que requieren un análisis más profundo.
Por ejemplo, considera la detección del fraude, que a menudo se resuelve utilizando modelos complejos como los GMM. Los humanos casi siempre investigan las transacciones de alto riesgo, independientemente del modelo utilizado. Por tanto, un enfoque alternativo es utilizar un árbol de decisión para marcar una lista de transacciones potencialmente fraudulentas para su posterior investigación manual.
Los árboles de decisión también se utilizan en muchas operaciones empresariales. El objetivo es decidir el curso de acción correcto en función de unas condiciones predeterminadas. Estas tareas no necesitan modelos generativos ni modelos discriminativos más complejos, como las redes neuronales.
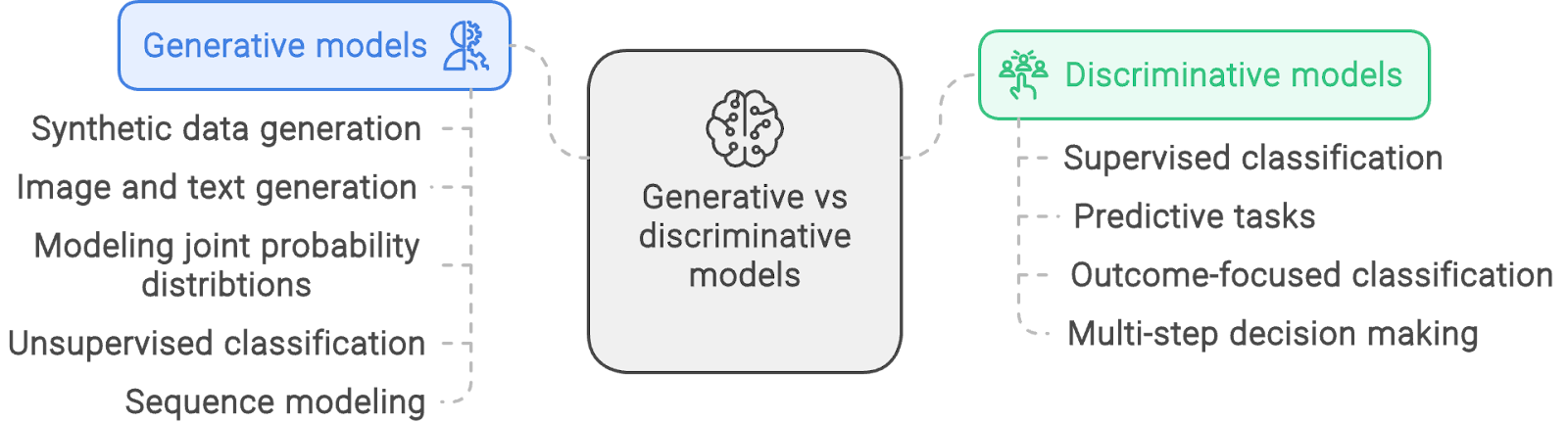
Ejemplos de aplicación de los modelos generativos frente a los discriminativos. Creado con napkin.ai
Conclusión
Este artículo explica los principios fundamentales y las principales diferencias entre los modelos generativos y discriminativos, los dos enfoques principales de las técnicas de aprendizaje automático.
Aunque la mayor parte del aprendizaje automático se basa en métodos probabilísticos, los modelos generativos se basan en la distribución de probabilidad conjunta, mientras que los modelos discriminativos sólo utilizan probabilidades condicionales. Por tanto, las dos clases de modelos tienen aplicaciones y características de rendimiento diferentes. Teniendo en cuenta la disponibilidad de una gran variedad de modelos, elegir la herramienta adecuada para el trabajo se convierte en algo esencial.
Más allá de la comprensión conceptual de los tipos de modelos y sus diferencias, lo más importante es que construyas tú mismo los modelos. Empieza con la entrada del blog que trata sobre los métodos de entrenamiento supervisado y la construcción de un modelo sencillo de regresión logística.
Preguntas frecuentes
¿Puedo utilizar modelos generativos para tareas de clasificación?
Sí, los modelos generativos también pueden utilizarse para tareas de clasificación, porque modelan la distribución de probabilidad conjunta subyacente. Estiman las probabilidades condicionales (para tareas de clasificación) mediante la regla de Bayes.
¿Puedo utilizar también modelos discriminativos para tareas generativas?
No, para las tareas generativas, el modelo debe captar la distribución de probabilidad multivariante conjunta y las probabilidades marginales de los datos. Los modelos discriminatorios sólo captan la probabilidad condicional. Por lo tanto, no pueden utilizarse para tareas generativas.
¿Qué tipo de modelo es correcto para las tareas de clasificación si el conjunto de datos de entrenamiento tiene datos ausentes o incompletos?
Los modelos discriminatorios tienen más probabilidades de sobreajustar el modelo al conjunto de datos. Así, cualquier deficiencia en el conjunto de datos se reflejará de forma más prominente en los parámetros del modelo. A los modelos generativos les resulta más fácil compensar los puntos de datos que faltan, porque modelan la distribución de los datos subyacentes. Por tanto, los modelos generativos son la mejor opción.
¿Qué modelos funcionan mejor en las tareas de clasificación?
Los cálculos subyacentes de los modelos discriminativos son más sencillos. Así, los modelos discriminativos rinden mejor en las tareas de clasificación.
Para una tarea generativa (o discriminativa), ¿puedo elegir cualquiera de los modelos generativos (o discriminativos)?
En algunos casos, sí. Pero en general, no. Tienes que elegir un modelo cuyos datos de entrenamiento y algoritmo se parezcan a tus datos y a los métodos que quieres aplicar.
Por ejemplo, aunque los modelos de Markov y los GAN son generativos, los primeros están especialmente indicados para datos secuenciales. Los GAN tienen un alcance más amplio, aunque tradicionalmente se han utilizado para tareas basadas en imágenes.
Del mismo modo, aunque los modelos Naive Bayes son generativos, se utilizan principalmente para tareas de clasificación.
Estudia los detalles de cada modelo y los casos de uso típicos para determinar cuál se adapta mejor a tu problema.