Perceptrons multicouches dans l'apprentissage automatique : Un guide complet

Les bases des réseaux neuronaux

Les réseaux neuronaux ou réseaux neuronaux artificiels sont des outils fondamentaux de l'apprentissage automatique, qui alimentent de nombreux algorithmes et applications de pointe dans divers domaines, notamment la vision par ordinateur, le traitement du langage naturel, la robotique, etc.

Un réseau neuronal se compose de nœuds interconnectés, appelés neurones, organisés en couches. Chaque neurone reçoit des signaux d'entrée, effectue un calcul sur ces signaux à l'aide d'une fonction d'activation et produit un signal de sortie qui peut être transmis à d'autres neurones du réseau. Une fonction d'activation détermine la sortie d'un neurone en fonction de son entrée. Ces fonctions introduisent une non-linéarité dans le réseau, ce qui lui permet d'apprendre des schémas complexes dans les données.

Le réseau est généralement organisé en couches, en commençant par la couche d'entrée, où les données sont introduites. Viennent ensuite les couches cachées où les calculs sont effectués et, enfin, la couche de sortie où les prédictions ou les décisions sont prises.

Les neurones des couches adjacentes sont reliés par des connexions pondérées, qui transmettent les signaux d'une couche à l'autre. La force de ces connexions, représentée par les poids, détermine l'influence de la sortie d'un neurone sur l'entrée d'un autre neurone. Au cours du processus de formation, le réseau apprend à ajuster ses poids sur la base d'exemples fournis dans un ensemble de données de formation. En outre, chaque neurone a généralement un biais associé, qui lui permet d'ajuster son seuil de sortie.

Les réseaux neuronaux sont formés à l'aide de techniques appelées propagation ascendante et rétropropagation. Lors de la propagation ascendante, les données d'entrée sont transmises au réseau couche par couche, chaque couche effectuant un calcul sur la base des données d'entrée qu'elle reçoit et transmettant le résultat à la couche suivante.

La rétropropagation est un algorithme utilisé pour former des réseaux neuronaux en ajustant de manière itérative les poids et les biais du réseau afin de minimiser la fonction de perte. Une fonction de perte (également appelée fonction de coût ou fonction objective) est une mesure de l'adéquation entre les prédictions du modèle et les vraies valeurs cibles dans les données d'apprentissage. La fonction de perte quantifie la différence entre la sortie prédite du modèle et la sortie réelle, fournissant un signal qui guide le processus d'optimisation pendant la formation.

L'objectif de la formation d'un réseau neuronal est de minimiser cette fonction de perte en ajustant les poids et les biais. Les ajustements sont guidés par un algorithme d'optimisation, tel que la descente de gradient. Nous reviendrons sur certains de ces sujets plus en détail dans la suite de ce tutoriel.

Types de réseaux neuronaux

Neurone biologique vs. Réseau neuronal artificiel Source : ResearchGate

L'ANN représenté à droite de l'image est un réseau neuronal simple appelé "perceptron". Il se compose d'une seule couche, qui est la couche d'entrée, avec plusieurs neurones dotés de leurs propres poids ; il n'y a pas de couches cachées. L'algorithme du perceptron apprend les poids des signaux d'entrée afin de tracer une frontière de décision linéaire.

Cependant, pour résoudre des problèmes non linéaires plus complexes liés au traitement d'images, à la vision par ordinateur et aux tâches de traitement du langage naturel, nous travaillons avec des réseaux neuronaux profonds.

Consultez le tutoriel Introduction aux réseaux neuronaux profonds de DataCamp pour en savoir plus sur les réseaux neuronaux profonds et comment en construire un à partir de zéro en utilisant TensorFlow et Keras en Python. Si vous préférez utiliser le langage R à la place, le cours Building Neural Network (NN) Models in R de DataCamp vous couvre.

Il existe plusieurs types d'ANN, chacun étant conçu pour des tâches et des exigences architecturales spécifiques. Examinons brièvement quelques-uns des types les plus courants avant de nous pencher plus avant sur les MLP.

Réseaux neuronaux progressifs (FNN)

Il s'agit de la forme la plus simple d'ANN, dans laquelle les informations circulent dans une seule direction, de l'entrée à la sortie. Il n'y a pas de cycles ou de boucles dans l'architecture du réseau. Les perceptrons multicouches (MLP) sont un type de réseau neuronal de type feedforward.

Réseaux neuronaux récurrents (RNN)

Dans les RNN, les connexions entre les nœuds forment des cycles dirigés, ce qui permet à l'information de persister dans le temps. Ils conviennent donc aux tâches impliquant des données séquentielles, telles que la prédiction de séries temporelles, le traitement du langage naturel et la reconnaissance vocale.

Réseaux neuronaux convolutifs (CNN)

Les CNN sont conçus pour traiter efficacement des données en forme de grille, telles que des images. Ils se composent de couches de filtres convolutifs qui apprennent les représentations hiérarchiques des caractéristiques des données d'entrée. Les CNN sont largement utilisés dans des tâches telles que la classification d'images, la détection d'objets et la segmentation d'images.

Réseaux de mémoire à long terme (LSTM) et unités récurrentes gérées (GRU)

Il s'agit de types spécialisés de réseaux neuronaux récurrents conçus pour résoudre le problème de l'évanouissement du gradient dans les réseaux neuronaux récurrents traditionnels. Les LSTM et les GRU intègrent des mécanismes à portes pour mieux capturer les dépendances à long terme dans les données séquentielles, ce qui les rend particulièrement efficaces pour des tâches telles que la reconnaissance vocale, la traduction automatique et l'analyse des sentiments.

Autoencoder

Il est conçu pour l'apprentissage non supervisé et se compose d'un réseau d'encodage qui comprime les données d'entrée dans un espace latent de dimension inférieure, et d'un réseau de décodage qui reconstruit l'entrée originale à partir de la représentation latente. Les autoencodeurs sont souvent utilisés pour la réduction de la dimensionnalité, le débruitage des données et la modélisation générative.

Réseaux adversoriels génératifs (GAN)

Les GAN sont constitués de deux réseaux neuronaux, un générateur et un discriminateur, entraînés simultanément dans un cadre compétitif. Le générateur apprend à générer des échantillons de données synthétiques qui ne se distinguent pas des données réelles, tandis que le discriminateur apprend à distinguer les échantillons réels des échantillons fictifs. Les GAN ont été largement utilisés pour générer des images, des vidéos et d'autres types de données réalistes.

Perceptrons multicouches

Un perceptron multicouche est un type de réseau neuronal feedforward composé de neurones entièrement connectés avec une fonction d'activation de type non linéaire. Il est largement utilisé pour distinguer les données qui ne sont pas linéairement séparables.

Les MLP ont été largement utilisés dans divers domaines, notamment la reconnaissance d'images, le traitement du langage naturel et la reconnaissance vocale. La flexibilité de leur architecture et leur capacité à approximer n'importe quelle fonction sous certaines conditions en font un élément fondamental de la recherche sur l'apprentissage profond et les réseaux neuronaux. Nous allons nous pencher plus en détail sur certains de ses concepts clés.

Couche d'entrée

La couche d'entrée se compose de nœuds ou de neurones qui reçoivent les données d'entrée initiales. Chaque neurone représente une caractéristique ou une dimension des données d'entrée. Le nombre de neurones dans la couche d'entrée est déterminé par la dimensionnalité des données d'entrée.

Couche cachée

Entre les couches d'entrée et de sortie, il peut y avoir une ou plusieurs couches de neurones. Chaque neurone d'une couche cachée reçoit des entrées de tous les neurones de la couche précédente (soit la couche d'entrée, soit une autre couche cachée) et produit une sortie qui est transmise à la couche suivante. Le nombre de couches cachées et le nombre de neurones dans chaque couche cachée sont des hyperparamètres qui doivent être déterminés pendant la phase de conception du modèle.

Couche de sortie

Cette couche est constituée de neurones qui produisent la sortie finale du réseau. Le nombre de neurones dans la couche de sortie dépend de la nature de la tâche. Dans la classification binaire, il peut y avoir un ou deux neurones en fonction de la fonction d'activation et représentant la probabilité d'appartenir à une classe, tandis que dans les tâches de classification multi-classes, il peut y avoir plusieurs neurones dans la couche de sortie.

Poids

Les neurones des couches adjacentes sont entièrement connectés les uns aux autres. Chaque connexion a un poids associé, qui détermine la force de la connexion. Ces poids sont appris au cours du processus de formation.

Neurones de biais

Outre les neurones d'entrée et les neurones cachés, chaque couche (à l'exception de la couche d'entrée) comprend généralement un neurone de biais qui fournit une entrée constante aux neurones de la couche suivante. Les neurones à biais ont leur propre poids associé à chaque connexion, qui est également appris au cours de la formation.

Le neurone de biais déplace effectivement la fonction d'activation des neurones de la couche suivante, ce qui permet au réseau d'apprendre un décalage ou un biais dans la limite de décision. En ajustant les poids connectés au neurone de biais, le MLP peut apprendre à contrôler le seuil d'activation et à mieux s'adapter aux données d'apprentissage.

Note : Il est important de noter que dans le contexte des MLP, le biais peut se référer à deux concepts liés mais distincts : le biais en tant que terme général dans l'apprentissage automatique et le neurone biaisé (défini ci-dessus). Dans l'apprentissage automatique général, le biais fait référence à l'erreur introduite par l'approximation d'un problème réel à l'aide d'un modèle simplifié. Le biais mesure la capacité du modèle à capturer les schémas sous-jacents des données. Un biais élevé indique que le modèle est trop simpliste et risque de ne pas correspondre aux données, tandis qu'un biais faible indique que le modèle capture bien les modèles sous-jacents.

Fonction d'activation

En règle générale, chaque neurone des couches cachées et de la couche de sortie applique une fonction d'activation à la somme pondérée de ses entrées. Les fonctions d'activation les plus courantes sont la sigmoïde, le tanh, la ReLU (Rectified Linear Unit) et la softmax. Ces fonctions introduisent une non-linéarité dans le réseau, ce qui lui permet d'apprendre des schémas complexes dans les données.

Formation par rétropropagation

Les MLP sont formés à l'aide de l'algorithme de rétropropagation, qui calcule les gradients d'une fonction de perte par rapport aux paramètres du modèle et met à jour les paramètres de manière itérative afin de minimiser la perte.

Fonctionnement d'un perceptron multicouche : Couche par couche

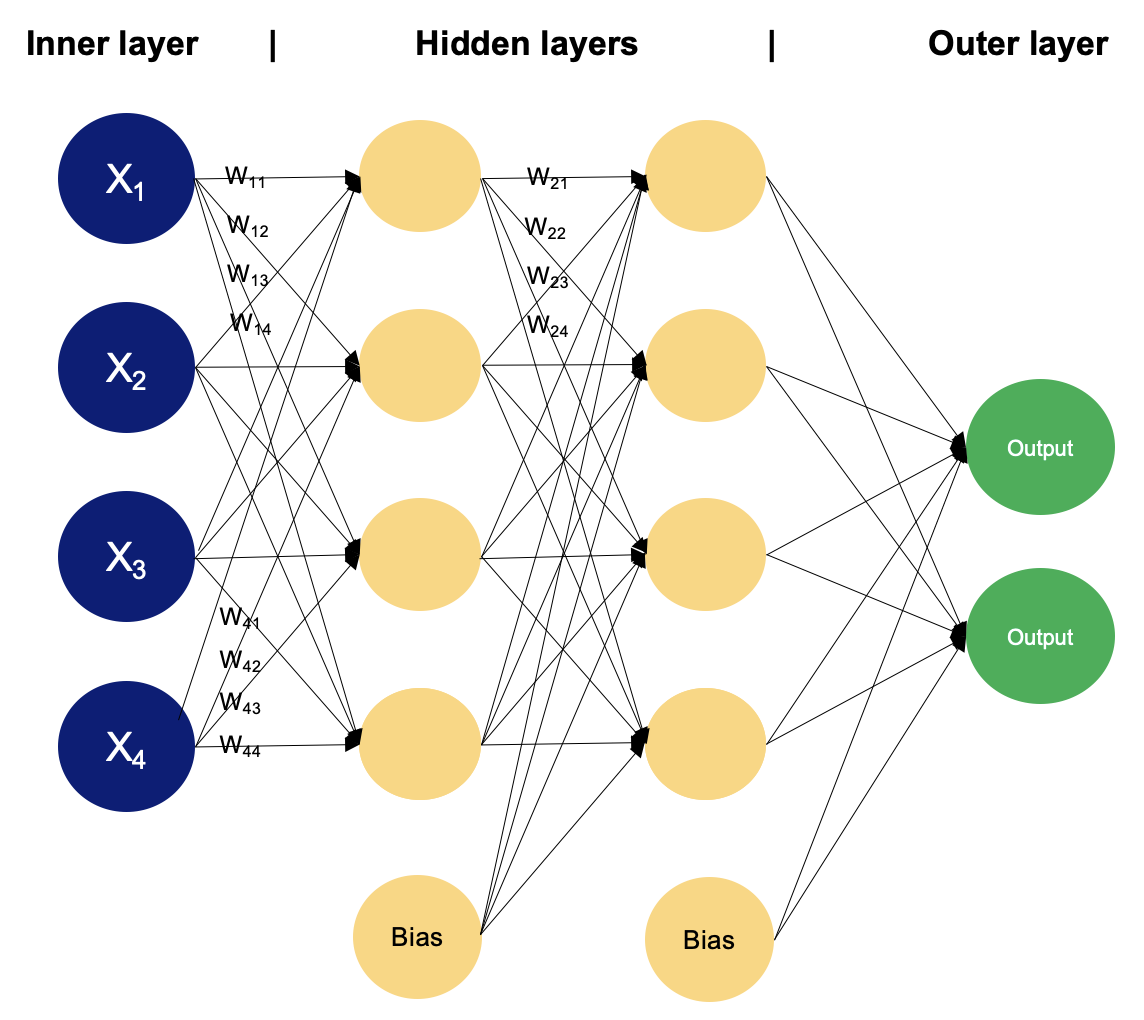
Exemple de MLP à deux couches cachées. Image par l'auteur

Dans un perceptron multicouche, les neurones traitent les informations étape par étape, en effectuant des calculs qui impliquent des sommes pondérées et des transformations non linéaires. Nous allons passer d'une couche à l'autre pour découvrir la magie qui s'y cache.

Couche d'entrée

• La couche d'entrée d'un MLP reçoit des données d'entrée, qui peuvent être des caractéristiques extraites des échantillons d'entrée d'un ensemble de données. Chaque neurone de la couche d'entrée représente une caractéristique.

• Les neurones de la couche d'entrée n'effectuent aucun calcul ; ils transmettent simplement les valeurs d'entrée aux neurones de la première couche cachée.

Couches cachées

• Les couches cachées d'un MLP sont constituées de neurones interconnectés qui effectuent des calculs sur les données d'entrée.

• Chaque neurone d'une couche cachée reçoit des informations de tous les neurones de la couche précédente. Les entrées sont multipliées par les poids correspondants, désignés par w. Les poids déterminent l'influence de l'entrée d'un neurone sur la sortie d'un autre.

• Outre les poids, chaque neurone de la couche cachée a un biais associé, désigné par b. Le biais fournit une entrée supplémentaire au neurone, lui permettant d'ajuster son seuil de sortie. Comme les poids, les biais sont appris au cours de la formation.
• Pour chaque neurone d'une couche cachée ou de la couche de sortie, la somme pondérée de ses entrées est calculée. Il s'agit de multiplier chaque entrée par son poids correspondant, d'additionner ces produits et d'ajouter le biais :

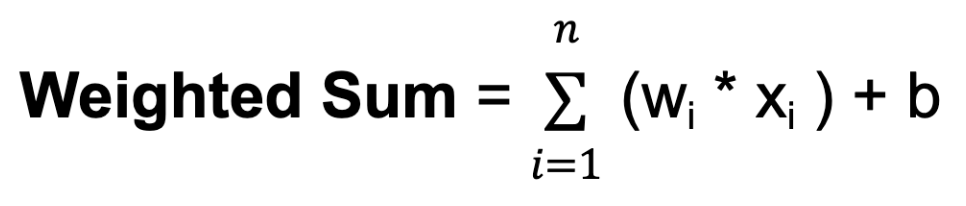
Où n est le nombre total de connexions d'entrée, wi est le poids de la i-ième entrée et xi est la i-ième valeur d'entrée.

• La somme pondérée passe ensuite par une fonction d'activation, désignée par f. La fonction d'activation introduit une non-linéarité dans le réseau, ce qui lui permet d'apprendre et de représenter des relations complexes dans les données. La fonction d'activation détermine la plage de sortie du neurone et son comportement en réponse à différentes valeurs d'entrée. Le choix de la fonction d'activation dépend de la nature de la tâche et des propriétés souhaitées du réseau.

Couche de sortie

• La couche de sortie d'un MLP produit les prédictions finales ou les sorties du réseau. Le nombre de neurones dans la couche de sortie dépend de la tâche à effectuer (par exemple, classification binaire, classification multi-classes, régression).

• Chaque neurone de la couche de sortie reçoit une entrée des neurones de la dernière couche cachée et applique une fonction d'activation. Cette fonction d'activation est généralement différente de celles utilisées dans les couches cachées et produit la valeur de sortie finale ou la prédiction.

Au cours du processus de formation, le réseau apprend à ajuster les poids associés aux entrées de chaque neurone afin de minimiser l'écart entre les sorties prédites et les vraies valeurs cibles dans les données de formation. En ajustant les poids et en apprenant les fonctions d'activation appropriées, le réseau apprend à approximer des modèles et des relations complexes dans les données, ce qui lui permet de faire des prédictions précises sur de nouveaux échantillons non vus.

Cet ajustement est guidé par un algorithme d'optimisation, tel que la descente stochastique de gradient (SGD), qui calcule les gradients d'une fonction de perte par rapport aux poids et met à jour les poids de manière itérative.

Examinons de plus près le fonctionnement du SGD.

Descente stochastique de gradient (SGD)

1. Initialisation : Le SGD commence par un ensemble initial de paramètres de modèle (poids et biais) de manière aléatoire ou à l'aide d'une méthode prédéfinie.

2. Optimisation itérative : L'objectif de cette étape est de trouver le minimum d'une fonction de perte, en se déplaçant itérativement dans la direction de la plus forte diminution de la valeur de la fonction.

Pour chaque itération (ou époque) de l'apprentissage :

• Mélangez les données d'apprentissage pour vous assurer que le modèle n'apprend pas à partir des mêmes modèles dans le même ordre à chaque fois.
• Divisez les données de formation en mini-lots (petits sous-ensembles de données).
• Pour chaque mini-lot :
• Calculez le gradient de la fonction de perte par rapport aux paramètres du modèle en utilisant uniquement les points de données du mini-lot. Cette estimation du gradient est une approximation stochastique du véritable gradient.
• Mettre à jour les paramètres du modèle en faisant un pas dans la direction opposée du gradient, à l'échelle d'un taux d'apprentissage:Θt+1 = θt - n * ⛛ J (θt)Où :θt représente les paramètres du modèle à l'itération t. Ce paramètre peut être le poids⛛ J (θt) est le gradient de la fonction de perte J par rapport aux paramètres θtn est le taux d'apprentissage, qui contrôle la taille des pas effectués pendant l'optimisation

3. Direction de la descente : Le gradient de la fonction de perte indique la direction de la montée la plus raide. Pour minimiser la fonction de perte, la descente de gradient se déplace dans la direction opposée, vers la descente la plus raide.

4. Taux d'apprentissage : La taille du pas effectué à chaque itération de la descente de gradient est déterminée par un paramètre appelé taux d'apprentissage, noté ci-dessus n. Ce paramètre contrôle la taille des pas effectués vers le minimum. Si le taux d'apprentissage est trop faible, la convergence peut être lente ; s'il est trop élevé, l'algorithme peut osciller ou diverger.

5. Convergence : Répétez le processus pendant un nombre fixe d'itérations ou jusqu'à ce qu'un critère de convergence soit rempli (par exemple, la modification de la fonction de perte est inférieure à un certain seuil).

La descente de gradient stochastique met à jour les paramètres du modèle plus fréquemment en utilisant des sous-ensembles de données plus petits, ce qui la rend efficace sur le plan informatique, en particulier pour les grands ensembles de données. Le caractère aléatoire introduit par SGD peut avoir un effet de régularisation, empêchant le modèle de s'adapter de manière excessive aux données d'apprentissage. Il est également bien adapté aux scénarios d'apprentissage en ligne dans lesquels de nouvelles données sont disponibles de manière incrémentielle, car il peut mettre à jour le modèle rapidement avec chaque nouveau point de données ou mini-lot.

Cependant, le SGD peut également présenter certains défis, tels que l'augmentation du bruit due à la nature stochastique de l'estimation du gradient et la nécessité de régler les hyperparamètres tels que le taux d'apprentissage. Diverses extensions et adaptations de la SGD, telles que la descente stochastique du gradient en mini-lots, le momentum et les méthodes de taux d'apprentissage adaptatif comme AdaGrad, RMSProp et Adam, ont été développées pour relever ces défis et améliorer la convergence et les performances.

Vous avez vu le fonctionnement des couches du perceptron multicouche et appris ce qu'est la descente de gradient stochastique ; pour terminer, il reste un dernier sujet à aborder : la rétropropagation.

Backpropagation

La rétropropagation est l'abréviation de "rétropropagation des erreurs". Dans le contexte de la rétropropagation, le SGD implique la mise à jour itérative des paramètres du réseau sur la base des gradients calculés lors de chaque lot de données d'apprentissage. Au lieu de calculer les gradients à partir de l'ensemble des données d'apprentissage (ce qui peut s'avérer coûteux en termes de calcul pour les grands ensembles de données), SGD calcule les gradients à partir de petits sous-ensembles aléatoires de données appelés mini-batchs. Voici un aperçu du fonctionnement de l'algorithme de rétropropagation :

1. Passe avant : Au cours de la passe avant, les données d'entrée sont introduites dans le réseau neuronal et la sortie du réseau est calculée couche par couche. Chaque neurone calcule une somme pondérée de ses entrées, applique une fonction d'activation au résultat et transmet la sortie aux neurones de la couche suivante.

2. Calcul de la perte : Après le passage en avant, la sortie du réseau est comparée aux vraies valeurs cibles et une fonction de perte est calculée pour mesurer l'écart entre la sortie prédite et la sortie réelle.

3. Passage en arrière (calcul du gradient) : Dans la passe arrière, les gradients de la fonction de perte par rapport aux paramètres du réseau (poids et biais) sont calculés à l'aide de la règle de la chaîne du calcul. Les gradients représentent le taux de variation de la fonction de perte par rapport à chaque paramètre et fournissent des informations sur la manière d'ajuster les paramètres pour réduire la perte.

4. Mise à jour des paramètres : Une fois les gradients calculés, les paramètres du réseau sont mis à jour dans la direction opposée aux gradients afin de minimiser la fonction de perte. Cette mise à jour est généralement effectuée à l'aide d'un algorithme d'optimisation tel que la descente de gradient stochastique (SGD), dont nous avons parlé précédemment.

5. Processus itératif : Les étapes 1 à 4 sont répétées de manière itérative pendant un nombre fixe d'époques ou jusqu'à ce que les critères de convergence soient remplis. À chaque itération, les paramètres du réseau sont ajustés sur la base des gradients calculés dans la passe arrière, ce qui permet de réduire progressivement la perte et d'améliorer les performances du modèle.

Préparation des données pour le perceptron multicouche

La préparation des données pour l'entraînement d'un MLP implique le nettoyage, le prétraitement, la mise à l'échelle, la division, le formatage et peut-être même l'augmentation des données. En fonction des fonctions d'activation utilisées et de l'échelle des caractéristiques d'entrée, il peut être nécessaire de standardiser ou de normaliser les données. Il est souvent nécessaire d'expérimenter différentes techniques de prétraitement et d'évaluer leur impact sur les performances du modèle afin de déterminer l'approche la plus adaptée à un ensemble de données et à une tâche particuliers.

• Nettoyage et prétraitement des données
• Traiter les valeurs manquantes : Supprimez ou imputez les valeurs manquantes dans l'ensemble de données.
• Coder les variables catégorielles : Convertir les variables catégorielles en représentations numériques, telles que l'encodage à un point.

• Mise à l'échelle des caractéristiques
• Normalisation ou standardisation : Rééchelonnez les caractéristiques à une échelle similaire pour vous assurer que le processus d'optimisation converge efficacement.
• Normalisation (normalisation du score Z) : Soustrayez la moyenne et divisez par l'écart-type de chaque caractéristique. Il centre les données autour de zéro et les met à l'échelle pour obtenir une variance unitaire.
• Normalisation (échelle Min-Max) : Mettre les caractéristiques à l'échelle d'une plage fixe, généralement comprise entre 0 et 1, en soustrayant la valeur minimale et en la divisant par la plage (max-min).

Pour en savoir plus sur la mise à l'échelle des fonctionnalités, consultez le cours Feature Engineering for Machine Learning in Python de DataCamp.

• Séparation formation-validation-test
• Divisez l'ensemble de données en ensembles de formation, de validation et de test. L'ensemble d'apprentissage est utilisé pour former le modèle, l'ensemble de validation est utilisé pour ajuster les hyperparamètres et contrôler les performances du modèle, et l'ensemble de test est utilisé pour évaluer les performances du modèle final sur des données inédites.

• Formatage des données
• Veillez à ce que les données soient présentées dans le format approprié pour la formation. Il peut s'agir de remodeler les données ou de les convertir au type de données requis (par exemple, convertir des variables catégorielles en variables numériques).

• Augmentation facultative des données
• Pour des tâches telles que la classification d'images, des techniques d'augmentation des données telles que la rotation, le retournement et la mise à l'échelle peuvent être appliquées pour accroître la diversité des données d'apprentissage et améliorer la généralisation du modèle.

• Fonctions de normalisation et d'activation
• Le choix entre la normalisation et la standardisation peut dépendre des fonctions d'activation utilisées dans le MLP. Les fonctions d'activation telles que sigmoïde et tanh sont sensibles à l'échelle des données d'entrée et peuvent bénéficier d'une normalisation. D'autre part, les fonctions d'activation telles que ReLU sont moins sensibles à l'échelle et peuvent ne pas nécessiter de normalisation.

Lignes directrices générales pour la mise en œuvre du perceptron multicouche

La mise en œuvre d'un MLP comporte plusieurs étapes, depuis le prétraitement des données jusqu'à l'entraînement et l'évaluation du modèle. La sélection du nombre de couches et de neurones pour un MLP implique de trouver un équilibre entre la complexité du modèle, le temps d'apprentissage et les performances de généralisation. Il n'existe pas de réponse unique, car l'architecture optimale dépend de facteurs tels que la complexité de la tâche, la quantité de données disponibles et les ressources informatiques. Cependant, voici quelques lignes directrices générales à prendre en compte lors de la mise en œuvre de la MLP :

1. Architecture du modèle

• Commencez par une architecture simple et augmentez progressivement la complexité si nécessaire. Commencez par une seule couche cachée et un petit nombre de neurones, puis expérimentez en ajoutant des couches et des neurones supplémentaires si nécessaire.

2. Complexité des tâches

• Pour les tâches simples et relativement peu complexes, telles que la classification binaire ou la régression sur de petits ensembles de données, une architecture peu profonde avec moins de couches et de neurones peut suffire.
• Pour des tâches plus complexes, telles que la classification multi-classes ou la régression sur des données de haute dimension, des architectures plus profondes avec plus de couches et de neurones peuvent être nécessaires pour capturer des modèles complexes dans les données.

3. Prétraitement des données

• Nettoyez et prétraitez vos données, notamment en traitant les valeurs manquantes, en codant les variables catégorielles et en mettant à l'échelle les caractéristiques numériques.
• Divisez vos données en ensembles de formation, de validation et de test afin d'évaluer les performances du modèle.

4. Initialisation

• Initialisez les poids et les biais de votre MLP de manière appropriée. Les techniques d'initialisation courantes comprennent l'initialisation aléatoire avec des poids faibles ou l'utilisation de techniques telles que l'initialisation Xavier ou He.

5. Expérimentation

• En fin de compte, la meilleure approche consiste à expérimenter différentes architectures, en variant le nombre de couches et de neurones, et à évaluer leurs performances de manière empirique.
• Utilisez des techniques telles que la validation croisée et l'ajustement des hyperparamètres pour explorer systématiquement différentes architectures et trouver celle qui est la plus performante pour la tâche à accomplir.

6. Formation

• Entraînez votre MLP à l'aide des données d'entraînement et contrôlez ses performances sur l'ensemble de validation.
• Expérimentez avec différentes tailles de lots, nombre d'époques et autres hyperparamètres pour trouver les paramètres d'apprentissage optimaux.
• Visualisez la progression de la formation à l'aide de mesures telles que les pertes et la précision pour diagnostiquer les problèmes et suivre la convergence.

7. Algorithme d'optimisation

• Expérimentez différents taux d'apprentissage et envisagez d'utiliser des techniques telles que les programmes de taux d'apprentissage ou les taux d'apprentissage adaptatifs.

8. Éviter le surajustement

• Veillez à ne pas suradapter le modèle aux données d'apprentissage en introduisant une complexité inutile.
• Utilisez des techniques telles que la régularisation (par exemple, régularisation L1, L2), l'abandon et l'arrêt précoce pour éviter l'ajustement excessif et améliorer les performances de généralisation.
• Ajustez la force de régularisation en fonction de la performance du modèle sur l'ensemble de validation.

9. Évaluation du modèle

• Contrôlez les performances du modèle sur un ensemble de validation distinct pendant la formation afin d'évaluer l'impact des modifications de l'architecture sur les performances.
• Évaluez le modèle formé sur l'ensemble de test afin d'évaluer ses performances en matière de généralisation.
• Utilisez des mesures telles que la précision, la perte et l'erreur de validation pour évaluer les performances du modèle et guider les décisions architecturales.

10. Répéter et expérimenter

• Expérimentez différentes architectures, hyperparamètres et stratégies d'optimisation pour améliorer les performances du modèle.
• Améliorez votre mise en œuvre en vous basant sur les connaissances acquises lors de la formation et sur les résultats de l'évaluation.

Conclusion

Les perceptrons multicouches représentent une classe fondamentale et polyvalente de réseaux neuronaux artificiels qui ont contribué de manière significative à l'avancement de l'apprentissage automatique et de l'intelligence artificielle. Grâce à leurs couches interconnectées de neurones et à leurs fonctions d'activation non linéaires, les MLP sont capables d'apprendre des modèles et des relations complexes dans les données, ce qui les rend bien adaptés à un large éventail de tâches. L'histoire des MLP reflète un voyage d'exploration, de découverte et d'innovation, depuis les premiers modèles de perceptron jusqu'aux architectures modernes d'apprentissage profond qui alimentent aujourd'hui de nombreux systèmes de pointe.

Dans cet article, vous avez appris les bases des réseaux neuronaux artificiels, vous vous êtes concentré sur les perceptrons multicouches et vous avez découvert la descente de gradient stochastique et la rétropropagation. Si vous souhaitez acquérir une expérience pratique et utiliser des techniques d'apprentissage profond pour résoudre des défis du monde réel, tels que la prédiction des prix des logements, la construction de réseaux neuronaux pour modéliser des images et du texte - nous vous recommandons vivement de suivre le cursus de la boîte à outils Keras de DataCamp.

En travaillant avec Keras, vous découvrirez les réseaux neuronaux, les flux de travail des modèles d'apprentissage profond et la manière d'optimiser vos modèles. DataCamp propose également une antisèche Keras qui peut s'avérer très pratique !