Multilayer Perceptrons in Machine Learning: Ein umfassender Leitfaden

Grundlagen der neuronalen Netze

Neuronale Netze oder künstliche neuronale Netze sind grundlegende Werkzeuge des maschinellen Lernens, die viele hochmoderne Algorithmen und Anwendungen in verschiedenen Bereichen, wie z.B. Computer Vision, natürliche Sprachverarbeitung, Robotik und mehr, unterstützen.

Ein neuronales Netzwerk besteht aus miteinander verbundenen Knoten, den Neuronen, die in Schichten organisiert sind. Jedes Neuron empfängt Eingangssignale, führt mithilfe einer Aktivierungsfunktion eine Berechnung durch und erzeugt ein Ausgangssignal, das an andere Neuronen im Netzwerk weitergeleitet werden kann. Eine Aktivierungsfunktion bestimmt die Ausgabe eines Neurons in Abhängigkeit von seiner Eingabe. Diese Funktionen bringen Nichtlinearität in das Netzwerk ein und ermöglichen es ihm, komplexe Muster in den Daten zu lernen.

Das Netz ist in der Regel in Schichten organisiert, beginnend mit der Eingabeschicht, in die die Daten eingegeben werden. Danach folgen die versteckten Schichten, in denen die Berechnungen durchgeführt werden, und schließlich die Ausgabeschicht, in der die Vorhersagen oder Entscheidungen getroffen werden.

Neuronen in benachbarten Schichten sind durch gewichtete Verbindungen verbunden, die Signale von einer Schicht zur nächsten übertragen. Die Stärke dieser Verbindungen, die durch Gewichte dargestellt werden, bestimmt, wie viel Einfluss die Ausgabe eines Neurons auf die Eingabe eines anderen Neurons hat. Während des Trainingsprozesses lernt das Netz, seine Gewichte anhand von Beispielen aus einem Trainingsdatensatz anzupassen. Außerdem hat jedes Neuron in der Regel eine Vorspannung (Bias), mit der das Neuron seine Ausgangsschwelle anpassen kann.

Neuronale Netze werden mit Techniken trainiert, die Feedforward Propagation und Backpropagation genannt werden. Bei der Feedforward-Fortpflanzung werden die Eingabedaten Schicht für Schicht durch das Netzwerk geleitet, wobei jede Schicht eine Berechnung auf der Grundlage der Eingaben durchführt, die sie erhält, und das Ergebnis an die nächste Schicht weitergibt.

Backpropagation ist ein Algorithmus, mit dem neuronale Netze trainiert werden, indem die Gewichte und Vorspannungen des Netzes iterativ angepasst werden, um die Verlustfunktion zu minimieren. Eine Verlustfunktion (auch bekannt als Kostenfunktion oder Zielfunktion) ist ein Maß dafür, wie gut die Vorhersagen des Modells mit den wahren Zielwerten in den Trainingsdaten übereinstimmen. Die Verlustfunktion quantifiziert die Differenz zwischen der vorhergesagten Leistung des Modells und der tatsächlichen Leistung und liefert ein Signal, das den Optimierungsprozess während des Trainings leitet.

Das Ziel des Trainings eines neuronalen Netzes ist es, diese Verlustfunktion zu minimieren, indem die Gewichte und Verzerrungen angepasst werden. Die Anpassungen werden durch einen Optimierungsalgorithmus, wie zum Beispiel den Gradientenabstieg, gesteuert. Auf einige dieser Themen werden wir später in diesem Lernprogramm noch einmal genauer eingehen.

Arten von neuronalen Netzwerken

Biologisches Neuron vs. Künstliches Neuronales Netzwerk Quelle: ResearchGate

Das ANN auf der rechten Seite des Bildes ist ein einfaches neuronales Netz namens "Perceptron". Sie besteht aus einer einzigen Schicht, der Eingabeschicht, mit mehreren Neuronen mit eigenen Gewichten; es gibt keine versteckten Schichten. Der Perceptron-Algorithmus lernt die Gewichte für die Eingangssignale, um eine lineare Entscheidungsgrenze zu ziehen.

Um jedoch kompliziertere, nicht-lineare Probleme in den Bereichen Bildverarbeitung, Computer Vision und Verarbeitung natürlicher Sprache zu lösen, arbeiten wir mit tiefen neuronalen Netzen.

Im Datacamp-Tutorial Einführung in tiefe neuronale Netze erfährst du mehr über tiefe neuronale Netze und wie du sie mit TensorFlow und Keras in Python von Grund auf neu konstruierst. Wenn du stattdessen lieber die Sprache R verwenden möchtest, findest du in Datacamps Building Neural Network (NN) Models in R alles, was du brauchst.

Es gibt verschiedene Arten von ANN, die jeweils für bestimmte Aufgaben und Architekturanforderungen entwickelt wurden. Bevor wir uns näher mit MLPs befassen, wollen wir kurz auf einige der gängigsten Typen eingehen.

Feedforward Neuronale Netze (FNN)

Dies ist die einfachste Form von ANNs, bei der die Informationen in eine Richtung fließen, von der Eingabe zur Ausgabe. In der Netzwerkarchitektur gibt es keine Zyklen oder Schleifen. Mehrschichtige Perceptrons (MLP) sind eine Art neuronales Netz mit Vorwärtskopplung.

Rekurrente Neuronale Netze (RNN)

In RNNs bilden die Verbindungen zwischen den Knoten gerichtete Zyklen, so dass die Informationen über die Zeit erhalten bleiben. Dadurch eignen sie sich für Aufgaben, bei denen es um sequenzielle Daten geht, wie z. B. die Vorhersage von Zeitreihen, die Verarbeitung natürlicher Sprache und die Spracherkennung.

Convolutional Neural Networks (CNN)

CNNs wurden entwickelt, um gitterartige Daten, wie z.B. Bilder, effektiv zu verarbeiten. Sie bestehen aus Schichten von Faltungsfiltern, die hierarchische Darstellungen von Merkmalen in den Eingabedaten lernen. CNNs werden häufig für Aufgaben wie Bildklassifizierung, Objekterkennung und Bildsegmentierung eingesetzt.

Netzwerke mit langem Kurzzeitgedächtnis (LSTM) und Gated Recurrent Units (GRU)

Dies sind spezielle Arten von rekurrenten neuronalen Netzen, die entwickelt wurden, um das Problem des verschwindenden Gradienten in traditionellen RNN zu lösen. LSTMs und GRUs enthalten Gated-Mechanismen, um weitreichende Abhängigkeiten in sequentiellen Daten besser zu erfassen, was sie besonders effektiv für Aufgaben wie Spracherkennung, maschinelle Übersetzung und Stimmungsanalyse macht.

Autoencoder

Es ist für unüberwachtes Lernen konzipiert und besteht aus einem Encoder-Netzwerk, das die Eingabedaten in einen niedrigdimensionalen latenten Raum komprimiert, und einem Decoder-Netzwerk, das die ursprüngliche Eingabe aus der latenten Darstellung rekonstruiert. Autoencoder werden häufig zur Dimensionalitätsreduktion, Datenentrauschung und generativen Modellierung eingesetzt.

Generative Adversarial Networks (GAN)

GANs bestehen aus zwei neuronalen Netzen, einem Generator und einem Diskriminator, die gleichzeitig in einem Wettbewerb trainiert werden. Der Generator lernt, synthetische Datenproben zu erzeugen, die von echten Daten nicht zu unterscheiden sind, während der Diskriminator lernt, zwischen echten und gefälschten Proben zu unterscheiden. GANs werden häufig eingesetzt, um realistische Bilder, Videos und andere Arten von Daten zu erzeugen.

Mehrschichtige Perceptrons

Ein mehrschichtiges Perzeptron ist eine Art neuronales Netz mit Vorwärtskopplung, das aus vollständig verbundenen Neuronen mit einer nichtlinearen Aktivierungsfunktion besteht. Sie wird häufig verwendet, um Daten zu unterscheiden, die nicht linear trennbar sind.

MLPs sind in verschiedenen Bereichen weit verbreitet, unter anderem in der Bilderkennung, der Verarbeitung natürlicher Sprache und der Spracherkennung. Ihre Flexibilität in der Architektur und die Fähigkeit, jede Funktion unter bestimmten Bedingungen zu approximieren, machen sie zu einem grundlegenden Baustein in der Deep Learning- und Neuronalnetzforschung. Wir wollen uns einige der wichtigsten Konzepte genauer ansehen.

Eingabeschicht

Die Eingabeschicht besteht aus Knoten oder Neuronen, die die ersten Eingabedaten erhalten. Jedes Neuron repräsentiert ein Merkmal oder eine Dimension der Eingabedaten. Die Anzahl der Neuronen in der Eingabeschicht wird durch die Dimensionalität der Eingabedaten bestimmt.

Verdeckte Schicht

Zwischen der Eingabe- und der Ausgabeschicht können sich eine oder mehrere Schichten von Neuronen befinden. Jedes Neuron in einer versteckten Schicht erhält Eingaben von allen Neuronen in der vorherigen Schicht (entweder der Eingabeschicht oder einer anderen versteckten Schicht) und erzeugt eine Ausgabe, die an die nächste Schicht weitergeleitet wird. Die Anzahl der versteckten Schichten und die Anzahl der Neuronen in jeder versteckten Schicht sind Hyperparameter, die in der Modellierungsphase festgelegt werden müssen.

Ausgangsschicht

Diese Schicht besteht aus Neuronen, die die endgültige Ausgabe des Netzes produzieren. Die Anzahl der Neuronen in der Ausgabeschicht hängt von der Art der Aufgabe ab. Bei der binären Klassifizierung kann es je nach Aktivierungsfunktion ein oder zwei Neuronen geben, die die Wahrscheinlichkeit der Zugehörigkeit zu einer Klasse repräsentieren, während es bei Klassifizierungsaufgaben mit mehreren Klassen mehrere Neuronen in der Ausgabeschicht geben kann.

Gewichte

Neuronen in benachbarten Schichten sind vollständig miteinander verbunden. Jeder Verbindung ist ein Gewicht zugeordnet, das die Stärke der Verbindung bestimmt. Diese Gewichte werden während des Trainingsprozesses gelernt.

Vorspannung Neuronen

Zusätzlich zu den Eingabe- und versteckten Neuronen enthält jede Schicht (außer der Eingabeschicht) in der Regel ein Bias-Neuron, das den Neuronen in der nächsten Schicht einen konstanten Input liefert. Die Neuronen haben für jede Verbindung eine eigene Gewichtung, die ebenfalls beim Training gelernt wird.

Das Bias-Neuron verschiebt die Aktivierungsfunktion der Neuronen in der nachfolgenden Schicht, so dass das Netzwerk einen Offset oder eine Verzerrung der Entscheidungsgrenze lernen kann. Durch die Anpassung der Gewichte, die mit dem Bias-Neuron verbunden sind, kann die MLP lernen, den Schwellenwert für die Aktivierung zu kontrollieren und die Trainingsdaten besser anzupassen.

Hinweis: Es ist wichtig zu beachten, dass sich der Begriff Bias im Zusammenhang mit MLPs auf zwei verwandte, aber unterschiedliche Konzepte beziehen kann: Bias als allgemeiner Begriff im maschinellen Lernen und das Bias-Neuron (wie oben definiert). Beim maschinellen Lernen im Allgemeinen bezieht sich die Verzerrung auf den Fehler, der durch die Annäherung eines realen Problems mit einem vereinfachten Modell entsteht. Der Bias misst, wie gut das Modell die zugrunde liegenden Muster in den Daten erfassen kann. Eine hohe Verzerrung deutet darauf hin, dass das Modell zu einfach ist und die Daten möglicherweise nicht richtig abbildet, während eine niedrige Verzerrung darauf hindeutet, dass das Modell die zugrunde liegenden Muster gut erfasst.

Aktivierungsfunktion

In der Regel wendet jedes Neuron in den verborgenen Schichten und der Ausgabeschicht eine Aktivierungsfunktion auf seine gewichtete Summe der Eingaben an. Gängige Aktivierungsfunktionen sind Sigmoid, tanh, ReLU (Rectified Linear Unit) und Softmax. Diese Funktionen führen Nichtlinearität in das Netzwerk ein und ermöglichen es ihm, komplexe Muster in den Daten zu lernen.

Training mit Backpropagation

MLPs werden mit dem Backpropagation-Algorithmus trainiert, der die Gradienten einer Verlustfunktion in Bezug auf die Parameter des Modells berechnet und die Parameter iterativ aktualisiert, um den Verlust zu minimieren.

Die Funktionsweise eines mehrschichtigen Perzeptrons: Schicht für Schicht

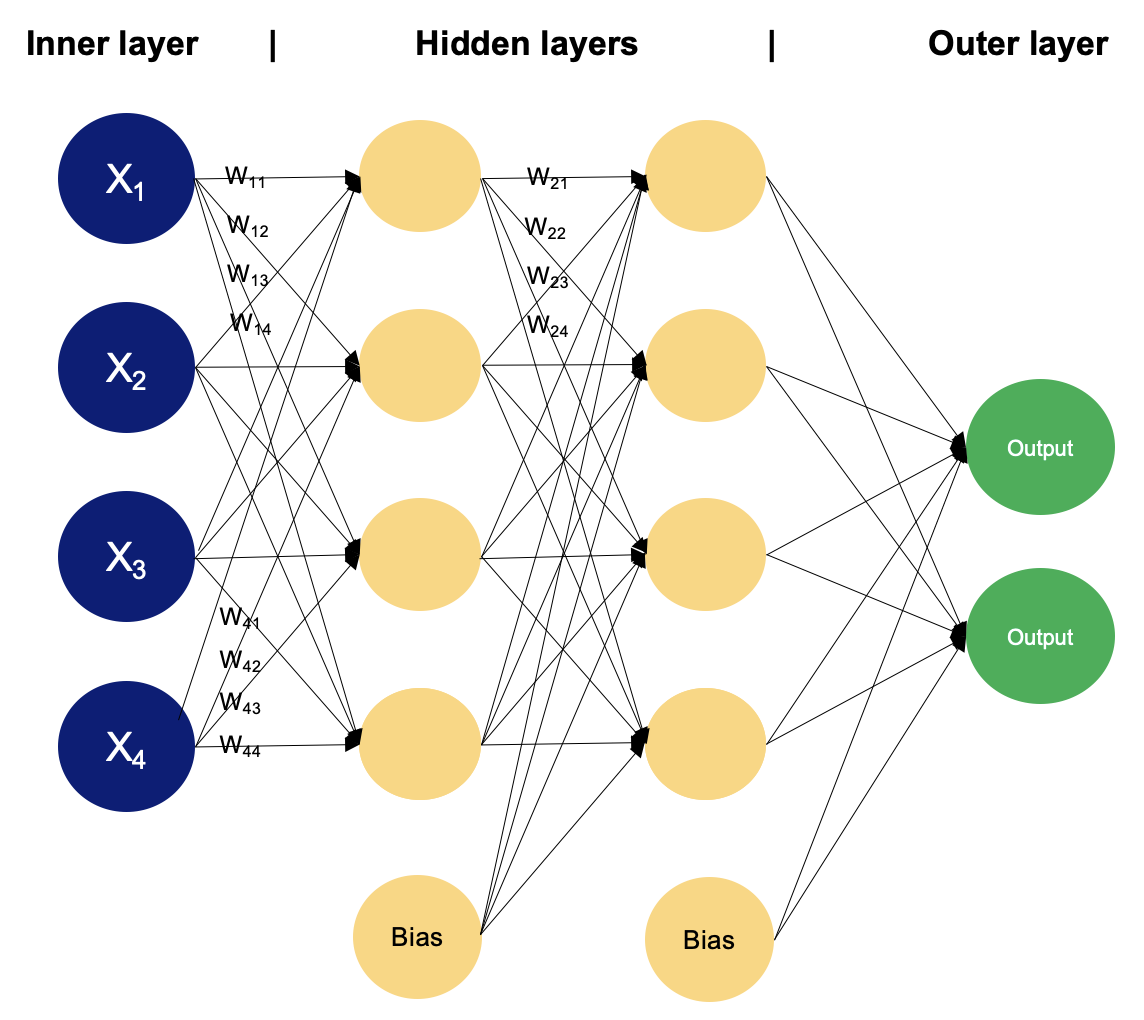
Beispiel für einen MLP mit zwei versteckten Schichten. Bild vom Autor

In einem mehrschichtigen Perzeptron verarbeiten die Neuronen Informationen schrittweise und führen Berechnungen durch, die gewichtete Summen und nichtlineare Transformationen beinhalten. Lass uns Schicht für Schicht gehen, um die Magie zu sehen, die darin steckt.

Eingabeschicht

• Die Eingabeschicht eines MLP empfängt Eingabedaten, die Merkmale sein können, die aus den Eingabeproben eines Datensatzes extrahiert werden. Jedes Neuron in der Eingabeschicht repräsentiert ein Merkmal.

• Die Neuronen in der Eingabeschicht führen keine Berechnungen durch; sie leiten die Eingabewerte einfach an die Neuronen in der ersten versteckten Schicht weiter.

Verborgene Schichten

• Die versteckten Schichten eines MLP bestehen aus miteinander verbundenen Neuronen, die Berechnungen mit den Eingabedaten durchführen.

• Jedes Neuron in einer versteckten Schicht erhält Input von allen Neuronen in der vorherigen Schicht. Die Eingaben werden mit entsprechenden Gewichten multipliziert, die als w bezeichnet werden. Die Gewichte bestimmen, wie viel Einfluss der Input eines Neurons auf den Output eines anderen hat.

• Zusätzlich zu den Gewichten hat jedes Neuron in der versteckten Schicht eine zugehörige Vorspannung, die als b bezeichnet wird. Die Vorspannung ist ein zusätzlicher Input für das Neuron, mit dem es seine Ausgangsschwelle anpassen kann. Wie Gewichte werden auch Vorurteile im Training erlernt.
• Für jedes Neuron in einer versteckten Schicht oder der Ausgabeschicht wird die gewichtete Summe seiner Eingaben berechnet. Dazu wird jeder Eingang mit dem entsprechenden Gewicht multipliziert, die Produkte werden addiert und die Vorspannung wird addiert:

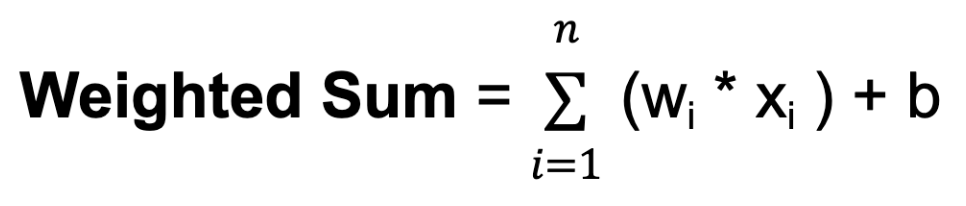
Dabei steht n für die Gesamtzahl der Eingangsverbindungen, wi für das Gewicht des i-ten Eingangs und xi für den i-ten Eingangswert.

• Die gewichtete Summe wird dann durch eine Aktivierungsfunktion geleitet, die als f bezeichnet wird. Die Aktivierungsfunktion führt Nichtlinearität in das Netz ein und ermöglicht es ihm, komplexe Beziehungen in den Daten zu lernen und darzustellen. Die Aktivierungsfunktion bestimmt den Ausgabebereich des Neurons und sein Verhalten als Reaktion auf verschiedene Eingabewerte. Die Wahl der Aktivierungsfunktion hängt von der Art der Aufgabe und den gewünschten Eigenschaften des Netzes ab.

Ausgangsschicht

• Die Ausgabeschicht eines MLP produziert die endgültigen Vorhersagen oder Ausgaben des Netzes. Die Anzahl der Neuronen in der Ausgabeschicht hängt von der jeweiligen Aufgabe ab (z. B. binäre Klassifizierung, Mehrklassen-Klassifizierung, Regression).

• Jedes Neuron in der Ausgabeschicht erhält Input von den Neuronen in der letzten versteckten Schicht und wendet eine Aktivierungsfunktion an. Diese Aktivierungsfunktion unterscheidet sich in der Regel von denen in den verborgenen Schichten und erzeugt den endgültigen Ausgabewert oder die Vorhersage.

Während des Trainingsprozesses lernt das Netzwerk, die Gewichte, die mit den Eingaben der einzelnen Neuronen verbunden sind, so anzupassen, dass die Diskrepanz zwischen den vorhergesagten Ausgaben und den wahren Zielwerten in den Trainingsdaten minimiert wird. Durch die Anpassung der Gewichte und das Erlernen geeigneter Aktivierungsfunktionen lernt das Netzwerk, komplexe Muster und Beziehungen in den Daten zu approximieren, so dass es bei neuen, ungesehenen Proben genaue Vorhersagen machen kann.

Diese Anpassung wird durch einen Optimierungsalgorithmus wie den stochastischen Gradientenabstieg (SGD) gesteuert, der die Gradienten einer Verlustfunktion in Bezug auf die Gewichte berechnet und die Gewichte iterativ aktualisiert.

Schauen wir uns genauer an, wie die SGD funktioniert.

Stochastischer Gradientenabstieg (SGD)

1. Initialisierung: SGD beginnt mit einer zufälligen oder vordefinierten Auswahl von Modellparametern (Gewichte und Verzerrungen).

2. Iterative Optimierung: Das Ziel dieses Schritts ist es, das Minimum einer Verlustfunktion zu finden, indem man sich iterativ in die Richtung des steilsten Abfalls des Funktionswerts bewegt.

Für jede Iteration (oder Epoche) des Trainings:

• Mische die Trainingsdaten, um sicherzustellen, dass das Modell nicht jedes Mal von denselben Mustern in derselben Reihenfolge lernt.
• Teile die Trainingsdaten in Mini-Batches (kleine Teilmengen von Daten) auf.
• Für jedes Minibatch:
• Berechne den Gradienten der Verlustfunktion in Bezug auf die Modellparameter, indem du nur die Datenpunkte im Mini-Batch verwendest. Diese Gradientenschätzung ist eine stochastische Annäherung an den wahren Gradienten.
• Aktualisiere die Modellparameter, indem du einen Schritt in die entgegengesetzte Richtung des Gradienten machst, skaliert mit einer Lernrate:Θt+1 = θt - n * ⛛ J (θt)Wobei:θt die Modellparameter in der Iteration t darstellt. Dieser Parameter kann das Gewicht sein⛛ J (θt) ist der Gradient der Verlustfunktion J in Bezug auf die Parameter θtn ist die Lernrate, die die Größe der während der Optimierung durchgeführten Schritte steuert

3. Richtung des Abstiegs: Der Gradient der Verlustfunktion gibt die Richtung des steilsten Anstiegs an. Um die Verlustfunktion zu minimieren, bewegt sich der Gradientenabstieg in die entgegengesetzte Richtung, in Richtung des steilsten Abstiegs.

4. Lernrate: Die Schrittweite, die in jeder Iteration des Gradientenabstiegs genommen wird, wird durch einen Parameter bestimmt, der als Lernrate bezeichnet wird und oben mit n bezeichnet wird. Dieser Parameter bestimmt die Größe der Schritte, die auf das Minimum zugehen. Ist die Lernrate zu klein, kann die Konvergenz langsam sein; ist sie zu groß, kann der Algorithmus oszillieren oder divergieren.

5. Konvergenz: Wiederhole den Prozess für eine festgelegte Anzahl von Iterationen oder bis ein Konvergenzkriterium erfüllt ist (z. B. wenn die Änderung der Verlustfunktion unter einem bestimmten Schwellenwert liegt).

Der stochastische Gradientenabstieg aktualisiert die Modellparameter häufiger unter Verwendung kleinerer Teilmengen von Daten, was ihn vor allem bei großen Datensätzen rechenintensiv macht. Die Zufälligkeit, die durch SGD eingeführt wird, kann einen Regularisierungseffekt haben, der verhindert, dass sich das Modell zu stark an die Trainingsdaten anpasst. Es eignet sich auch gut für Online-Lernszenarien, bei denen neue Daten schrittweise verfügbar werden, da es das Modell mit jedem neuen Datenpunkt oder Mini-Batch schnell aktualisieren kann.

SGD kann jedoch auch einige Herausforderungen mit sich bringen, wie z. B. ein erhöhtes Rauschen aufgrund der stochastischen Natur der Gradientenschätzung und die Notwendigkeit, Hyperparameter wie die Lernrate einzustellen. Verschiedene Erweiterungen und Anpassungen von SGD, wie der stochastische Mini-Batch-Gradientenabstieg, Momentum und adaptive Lernratenmethoden wie AdaGrad, RMSProp und Adam, wurden entwickelt, um diese Herausforderungen zu bewältigen und die Konvergenz und Leistung zu verbessern.

Du hast die Funktionsweise der mehrschichtigen Perzeptron-Schichten gesehen und etwas über den stochastischen Gradientenabstieg gelernt.

Backpropagation

Backpropagation ist die Abkürzung für "Rückwärtsausbreitung von Fehlern". Im Zusammenhang mit Backpropagation bedeutet SGD, dass die Parameter des Netzes iterativ auf der Grundlage der Gradienten aktualisiert werden, die bei jedem Stapel von Trainingsdaten berechnet werden. Anstatt die Gradienten anhand des gesamten Trainingsdatensatzes zu berechnen (was bei großen Datensätzen sehr rechenintensiv sein kann), berechnet SGD die Gradienten anhand kleiner zufälliger Teilmengen der Daten, den sogenannten Mini-Batches. Hier ist ein Überblick darüber, wie der Backpropagation-Algorithmus funktioniert:

1. Vorwärtspass: Beim Vorwärtsdurchlauf werden die Eingabedaten in das neuronale Netz eingespeist, und die Ausgabe des Netzes wird Schicht für Schicht berechnet. Jedes Neuron berechnet eine gewichtete Summe seiner Eingaben, wendet auf das Ergebnis eine Aktivierungsfunktion an und gibt die Ausgabe an die Neuronen in der nächsten Schicht weiter.

2. Verlustberechnung: Nach dem Vorwärtsdurchlauf wird die Ausgabe des Netzes mit den wahren Zielwerten verglichen und eine Verlustfunktion berechnet, um die Diskrepanz zwischen der vorhergesagten Ausgabe und der tatsächlichen Ausgabe zu messen.

3. Rückwärtspass (Gradientenberechnung): Im Backward-Pass werden die Gradienten der Verlustfunktion in Bezug auf die Parameter des Netzes (Gewichte und Verzerrungen) mithilfe der Kettenregel der Infinitesimalrechnung berechnet. Die Gradienten stellen die Änderungsrate der Verlustfunktion in Bezug auf die einzelnen Parameter dar und geben Aufschluss darüber, wie die Parameter angepasst werden müssen, um den Verlust zu verringern.

4. Parameter aktualisieren: Sobald die Gradienten berechnet sind, werden die Parameter des Netzes in die entgegengesetzte Richtung der Gradienten aktualisiert, um die Verlustfunktion zu minimieren. Diese Aktualisierung wird in der Regel mit einem Optimierungsalgorithmus wie dem stochastischen Gradientenabstieg (SGD) durchgeführt, den wir bereits besprochen haben.

5. Iterativer Prozess: Die Schritte 1-4 werden iterativ für eine bestimmte Anzahl von Epochen oder bis zum Erreichen der Konvergenzkriterien wiederholt. Bei jeder Iteration werden die Parameter des Netzes auf der Grundlage der im Backward Pass berechneten Gradienten angepasst, wodurch der Verlust schrittweise verringert und die Leistung des Modells verbessert wird.

Datenaufbereitung für Multilayer Perceptron

Zur Vorbereitung der Daten für das Training einer MLP gehört das Bereinigen, Vorverarbeiten, Skalieren, Aufteilen, Formatieren und vielleicht sogar das Erweitern der Daten. Je nach den verwendeten Aktivierungsfunktionen und der Skala der Eingangsmerkmale müssen die Daten möglicherweise standardisiert oder normalisiert werden. Das Experimentieren mit verschiedenen Vorverarbeitungstechniken und die Bewertung ihrer Auswirkungen auf die Modellleistung ist oft notwendig, um den am besten geeigneten Ansatz für einen bestimmten Datensatz und eine bestimmte Aufgabe zu ermitteln.

• Datenbereinigung und Vorverarbeitung
• Behandle fehlende Werte: Entferne oder ergänze fehlende Werte im Datensatz.
• Kodiere kategoriale Variablen: Wandle kategoriale Variablen in numerische Darstellungen um, z. B. in eine Ein-Hot-Codierung.

• Merkmal Skalierung
• Standardisierung oder Normalisierung: Skaliere die Merkmale auf einen ähnlichen Maßstab um, um sicherzustellen, dass der Optimierungsprozess effizient konvergiert.
• Standardisierung (Z-Score-Normalisierung): Ziehe den Mittelwert ab und teile ihn durch die Standardabweichung jedes Merkmals. Sie zentriert die Daten um Null und skaliert sie so, dass sie eine Einheitsvarianz haben.
• Normalisierung (Min-Max-Skalierung): Skaliere die Merkmale auf einen festen Bereich, normalerweise zwischen 0 und 1, indem du den Minimalwert abziehst und durch den Bereich teilst (max-min).

Wenn du mehr über die Skalierung von Funktionen erfahren möchtest, schau dir den Kurs Feature Engineering for Machine Learning in Python von Datacamp an.

• Train-Validation-Test Aufteilung
• Teile den Datensatz in Trainings-, Validierungs- und Testdatensätze auf. Die Trainingsmenge wird zum Trainieren des Modells verwendet, die Validierungsmenge zum Abstimmen der Hyperparameter und zum Überwachen der Modellleistung, und die Testmenge zum Bewerten der Leistung des endgültigen Modells bei ungesehenen Daten.

• Datenformatierung
• Achte darauf, dass die Daten in einem für die Ausbildung geeigneten Format vorliegen. Dazu kann es notwendig sein, die Daten umzuformen oder sie in den gewünschten Datentyp umzuwandeln (z. B. kategorische Variablen in numerische umzuwandeln).

• Optionale Datenerweiterung
• Bei Aufgaben wie der Bildklassifizierung können Techniken zur Datenerweiterung wie Drehen, Spiegeln und Skalieren eingesetzt werden, um die Vielfalt der Trainingsdaten zu erhöhen und die Modellgeneralisierung zu verbessern.

• Normalisierungs- und Aktivierungsfunktionen
• Die Wahl zwischen Standardisierung und Normalisierung kann von den im MLP verwendeten Aktivierungsfunktionen abhängen. Aktivierungsfunktionen wie Sigmoid und tanh reagieren empfindlich auf die Skalierung der Eingabedaten und können von einer Standardisierung profitieren. Andererseits reagieren Aktivierungsfunktionen wie ReLU weniger empfindlich auf die Skala und müssen möglicherweise nicht standardisiert werden.

Allgemeine Richtlinien für die Implementierung von Multilayer Perceptron

Die Implementierung eines MLP umfasst mehrere Schritte, von der Vorverarbeitung der Daten bis hin zum Training und der Auswertung des Modells. Bei der Auswahl der Anzahl der Schichten und Neuronen für ein MLP geht es darum, die Komplexität des Modells, die Trainingszeit und die Generalisierungsleistung abzuwägen. Es gibt keine pauschale Antwort, denn die optimale Architektur hängt von Faktoren wie der Komplexität der Aufgabe, der Menge der verfügbaren Daten und den Rechenressourcen ab. Hier sind jedoch einige allgemeine Richtlinien, die du bei der Umsetzung von MLP beachten solltest:

1. Modellarchitektur

• Beginne mit einer einfachen Architektur und steigere die Komplexität schrittweise nach Bedarf. Beginne mit einer einzigen versteckten Schicht und einer kleinen Anzahl von Neuronen und experimentiere dann mit dem Hinzufügen weiterer Schichten und Neuronen, falls nötig.

2. Komplexität der Aufgabe

• Für einfache Aufgaben mit relativ geringer Komplexität, wie z. B. binäre Klassifizierung oder Regression auf kleinen Datensätzen, kann eine flache Architektur mit weniger Schichten und Neuronen ausreichen.
• Für komplexere Aufgaben, wie z. B. die Klassifizierung mehrerer Klassen oder die Regression hochdimensionaler Daten, können tiefere Architekturen mit mehr Schichten und Neuronen erforderlich sein, um komplizierte Muster in den Daten zu erfassen.

3. Vorverarbeitung der Daten

• Bereinige deine Daten und verarbeite sie vor, indem du fehlende Werte behandelst, kategoriale Variablen kodierst und numerische Merkmale skalierst.
• Teile deine Daten in Trainings-, Validierungs- und Testmengen auf, um die Leistung des Modells zu bewerten.

4. Initialisierung

• Initialisiere die Gewichte und Vorspannungen deines MLP entsprechend. Zu den gängigen Initialisierungstechniken gehören die zufällige Initialisierung mit kleinen Gewichten oder Techniken wie die Xavier- oder He-Initialisierung.

5. Experimentieren

• Letztendlich ist es am besten, mit verschiedenen Architekturen zu experimentieren, die Anzahl der Schichten und Neuronen zu variieren und ihre Leistung empirisch zu bewerten.
• Nutze Techniken wie Kreuzvalidierung und Hyperparameter-Tuning, um systematisch verschiedene Architekturen zu untersuchen und diejenige zu finden, die für die jeweilige Aufgabe am besten geeignet ist.

6. Ausbildung

• Trainiere deine MLP mit den Trainingsdaten und überwache ihre Leistung in der Validierungsmenge.
• Experimentiere mit verschiedenen Stapelgrößen, der Anzahl der Epochen und anderen Hyperparametern, um die optimalen Trainingseinstellungen zu finden.
• Visualisiere den Trainingsfortschritt anhand von Kennzahlen wie Verlust und Genauigkeit, um Probleme zu diagnostizieren und die Konvergenz zu verfolgen.

7. Optimierungsalgorithmus

• Experimentiere mit verschiedenen Lerngeschwindigkeiten und ziehe Techniken wie Lerngeschwindigkeitszeitpläne oder adaptive Lerngeschwindigkeiten in Betracht.

8. Überanpassung vermeiden

• Achte darauf, dass du das Modell nicht zu sehr an die Trainingsdaten anpasst, indem du es unnötig komplex machst.
• Nutze Techniken wie Regularisierung (z. B. L1-, L2-Regularisierung), Dropout und frühzeitiges Stoppen, um eine Überanpassung zu verhindern und die Generalisierungsleistung zu verbessern.
• Stimme die Stärke der Regularisierung auf der Grundlage der Leistung des Modells in der Validierungsmenge ab.

9. Modellbewertung

• Überprüfe die Leistung des Modells während des Trainings auf einem separaten Validierungsset, um festzustellen, wie sich Änderungen der Architektur auf die Leistung auswirken.
• Evaluiere das trainierte Modell auf der Testmenge, um seine Generalisierungsleistung zu bewerten.
• Nutze Messgrößen wie Genauigkeit, Verlust und Validierungsfehler, um die Leistung des Modells zu bewerten und Entscheidungen über die Architektur zu treffen.

10. Iterieren und experimentieren

• Experimentiere mit verschiedenen Architekturen, Hyperparametern und Optimierungsstrategien, um die Leistung des Modells zu verbessern.
• Verbessere deine Umsetzung auf der Grundlage der Erkenntnisse aus der Schulung und den Bewertungsergebnissen.

Fazit

Mehrschichtige Perceptrons sind eine grundlegende und vielseitige Klasse künstlicher neuronaler Netze, die wesentlich zum Fortschritt des maschinellen Lernens und der künstlichen Intelligenz beigetragen haben. Durch ihre miteinander verbundenen Schichten von Neuronen und nichtlinearen Aktivierungsfunktionen sind MLPs in der Lage, komplexe Muster und Beziehungen in Daten zu lernen, wodurch sie sich für eine Vielzahl von Aufgaben eignen. Die Geschichte der MLPs spiegelt eine Reise der Erforschung, Entdeckung und Innovation wider, von den frühen Perceptron-Modellen bis hin zu den modernen Deep-Learning-Architekturen, die heute viele hochmoderne Systeme antreiben.

In diesem Artikel hast du die Grundlagen künstlicher neuronaler Netze kennengelernt, dich mit mehrschichtigen Perceptrons beschäftigt und etwas über stochastischen Gradientenabstieg und Backpropagation gelernt. Wenn du daran interessiert bist, praktische Erfahrungen zu sammeln und Deep-Learning-Techniken zu nutzen, um reale Herausforderungen zu lösen, wie z. B. die Vorhersage von Immobilienpreisen oder den Aufbau neuronaler Netze zur Modellierung von Bildern und Texten, empfehlen wir dir den Keras-Toolbox-Track des Datacamps.

Bei der Arbeit mit Keras lernst du etwas über neuronale Netze, Deep-Learning-Modell-Workflows und wie du deine Modelle optimierst. Datacamp hat auch einen Keras-Spickzettel, der sehr nützlich sein kann!