Matriz ortogonal: Una explicación con ejemplos y código

Una matriz ortogonal es una matriz cuadrada cuyas columnas y filas forman bases ortonormales, lo que significa que son ortogonales entre sí y tienen longitud unitaria. Esta propiedad aparentemente sencilla desbloquea capacidades útiles: conservan distancias, ángulos y productos internos cuando se aplican como transformaciones lineales. 

En este artículo, primero definiremos qué es una matriz ortogonal y examinaremos sus principales propiedades y ejemplos. Luego exploraremos aplicaciones prácticas, contrastaremos las matrices ortogonales con las ortonormales y demostraremos cómo identificar una matriz ortogonal en la práctica. Al comprender estas matrices especiales, obtendrás conocimientos sobre diversas técnicas computacionales utilizadas en la ciencia de datos, el machine learning y la computación numérica.

¿Qué es una matriz ortogonal?

Una matriz ortogonal es una matriz cuadrada Q cuyo transpuesto es igual a su inversa:

Definición de matriz ortogonal. Imagen del autor.

Cuando multiplicamos una matriz ortogonal por su transpuesta, obtenemos la matriz identidad:

Definición de matriz ortogonal. Imagen del autor.

Desde una perspectiva geométrica, una matriz ortogonal representa una transformación lineal que conserva la longitud de los vectores y los ángulos entre ellos. Dichas transformaciones incluyen rotaciones, reflexiones o combinaciones de estas operaciones en el espacio n-dimensional. Esto significa que cuando multiplicamos un vector por una matriz ortogonal, sólo cambia su orientación, no su magnitud.

Otra forma de entender las matrices ortogonales es a través de su estructura. En una matriz ortogonal, todas las columnas forman un conjunto ortonormal de vectores: cada columna tiene longitud unitaria (norma = 1), y cada par de columnas diferentes es ortogonal entre sí (su producto escalar es igual a cero). La misma propiedad se aplica a las filas de la matriz.

Para que una matriz de 2×2 sea ortogonal, por ejemplo, sus columnas deben ser vectores unitarios perpendiculares entre sí. Esto crea una transformación geométrica rígida que conserva la estructura del espacio sobre el que opera, lo que convierte a las matrices ortogonales en herramientas fundamentales en aplicaciones que requieren integridad geométrica.

Propiedades de las matrices ortogonales

Partiendo de la definición fundamental, a continuación exploraremos las propiedades matemáticas y computacionales que hacen que las matrices ortogonales tengan un valor incalculable en las aplicaciones numéricas.

Clasificación de los determinantes 

El determinante de una matriz ortogonal es siempre +1 o -1, lo que clasifica a estas matrices en dos categorías geométricas:

• Cuando det(Q) = +1, la matriz representa una rotación pura
• Cuando det(Q) = -1, la matriz representa una reflexión (o una rotación combinada con una reflexión)

Esta restricción determinante garantiza que las transformaciones ortogonales conserven el volumen, reorientando el espacio en lugar de estirarlo o comprimirlo.

Propiedades de conservación 

Las matrices ortogonales mantienen las relaciones geométricas durante la transformación. 

Para cualquier matriz ortogonal Q y vectores u y v:

• Se conservan las normas vectoriales: ||Qu|| = ||u||
• Se mantienen los productos internos: (Qu) - (Qv) = u - v
• Los ángulos entre vectores no cambian

Esta conservación va más allá de los vectores individuales: configuraciones geométricas enteras mantienen su estructura relativa bajo transformaciones ortogonales.

Propiedades algebraicas 

Los valores propios de las matrices ortogonales tienen todos valor absoluto igual a 1. Para las matrices ortogonales reales, estos valores propios son 1, -1 o aparecen en pares complejos conjugados en el círculo unitario. Esta restricción garantiza que la transformación no amplifique ni disminuya la "energía" global del sistema.

Además, el producto de dos matrices ortogonales es siempre ortogonal, lo que crea una propiedad de cierre que hace que estas matrices se comporten bien en transformaciones complejas y algoritmos iterativos.

Estabilidad numérica 

Desde un punto de vista computacional, las matrices ortogonales poseen propiedades numéricas excepcionales. Tienen un número de condición 1, lo que las hace extremadamente estables para los algoritmos numéricos. Esto significa que los pequeños errores de entrada no se magnifican durante el cálculo, lo que da lugar a resultados fiables y precisos incluso en cálculos complejos. Esta estabilidad es la razón por la que se prefieren las matrices ortogonales en muchos métodos numéricos y por la que algoritmos como la descomposición QR dependen en gran medida de las transformaciones ortogonales.

Ahora que hemos comprendido la definición y las propiedades que hacen especiales a las matrices ortogonales, veamos algunos ejemplos para entenderlas mejor.

Ejemplos de matrices ortogonales

La comprensión de las matrices ortogonales se aclara cuando exploramos matrices de ejemplo.

La matriz identidad

La matriz ortogonal más básica es la matriz identidad, que deja todos los vectores inalterados:

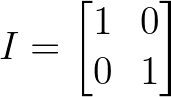
Matriz de identidad. Imagen del autor.

Aunque trivial, la matriz identidad satisface nuestro requisito fundamental: I^T × I = I, lo que la hace ortogonal por definición.

Matrices de rotación 2D

Uno de los ejemplos más intuitivos es una matriz de rotación 2D que gira vectores un ángulo θ:

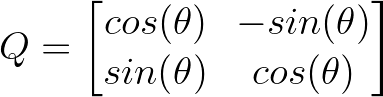
Matriz 2D. Imagen del autor.

Por ejemplo, girando 45 grados (π/4 radianes) nos da:

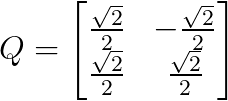
Matriz girada 45 grados. Imagen del autor.

Esta matriz gira cualquier vector 45 grados en el sentido contrario a las agujas del reloj, conservando su longitud: un ejemplo perfecto de transformación ortogonal que conserva las propiedades geométricas.

Matrices de reflexión

Las matrices de reflexión voltean vectores a través de un eje o plano concreto. Una reflexión simple a través del eje x es:

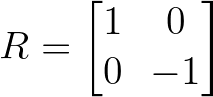
Ejemplo de matriz de reflexión. Imagen del autor.

Esta matriz mantiene inalterada la coordenada x y anula la coordenada y, de hecho, refleja los vectores en el eje horizontal.

Transformaciones 3D

Ampliando a tres dimensiones, podemos crear matrices de rotación para el espacio 3D. Una rotación alrededor del eje z con un ángulo θ tiene el siguiente aspecto:

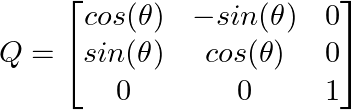
Realizar transformaciones 3D. Imagen del autor.

Observa cómo se conserva la coordenada z y se rotan los componentes x e y, demostrando cómo las matrices ortogonales pueden transformar selectivamente dimensiones específicas.

Cada uno de estos ejemplos demuestra el principio básico de las matrices ortogonales: transforman los vectores conservando sus propiedades geométricas esenciales: las longitudes no cambian y los ángulos entre vectores se mantienen.

Aplicaciones prácticas de las matrices ortogonales

Las matrices ortogonales se utilizan mucho en diversos campos debido a sus propiedades geométricas y numéricas. 

Algunas de ellas son:

• Análisis de componentes principales: El ACP utilizazas matrices ortogonales para transformar los datos en un nuevo sistema de coordenadas en el que la mayor varianza se encuentra a lo largo de la primera coordenada. La matriz de transformación está formada por vectores propios ortogonales que conservan la estructura geométrica de los datos al tiempo que reducen la dimensionalidad.
• Descomposición QR: Toda matriz puede descomponerse en como A = QR, donde Q es ortogonal y R es triangular superior. Esta descomposición es fundamental para resolver sistemas lineales, problemas de mínimos cuadrados y cálculos de valores propios.
• Infografía y transformaciones 3D Las matrices ortogonales son esenciales para las rotaciones 3D en infografía, robótica y visión por ordenador. Garantizan que los objetos mantengan su forma y tamaño durante las rotaciones, evitando distorsiones.
• Tratamiento de señales: La Transformada Discreta de Coseno (DCT) y la Transformada Discreta de Fourier utilizan matrices ortogonales para transformar señales entre los dominios del tiempo y la frecuencia. La compresión JPEG se basa en gran medida en la DCT, que utiliza transformaciones ortogonales.
• La informática cuántica: Las puertas cuánticas se representan mediante matrices unitarias, que son la generalización compleja de las matrices ortogonales. Estas transformaciones preservan las amplitudes de probabilidad en los sistemas cuánticos.

Ortogonal vs. Matrices ortonormales

A veces se confunden los términos matriz ortogonal y matriz ortonormal, pero en el contexto de las matrices sólo se utiliza la matriz ortogonal, que ya implica la ortonormalidad. La confusión suele surgir al mezclar la terminología de los conjuntos vectoriales con la de las matrices.

Para contrastar ambos:

• Un conjunto ortogonal de vectores está formado por vectores perpendiculares entre sí, pero no necesariamente de longitud unitaria.
• Un conjunto ortonormal está formado por vectores perpendiculares entre sí y de longitud unitaria (es decir, normalizados).

Entonces surge la confusión: ¿por qué lo llamamos "Ortogonal" y no "Ortonormal"?

Aunque las columnas de una matriz ortogonal son técnicamente ortonormales, el término matriz ortogonal es el nombre estándar, históricamente establecido en álgebra lineal. La etiqueta "matriz ortonormal" es redundante y rara vez, o nunca, se utiliza en matemáticas formales.

Cuando decimos que una matriz es ortogonal, siempre queremos decir que sus columnas (y filas) son ortonormales, es decir, mutuamente perpendiculares y de longitud unitaria. En este contexto no es necesario un término aparte como "matriz ortonormal".

Ahora que hemos aclarado la confusión con los nombres, vamos a averiguar cómo identificar una matriz ortogonal.

Cómo identificar una matriz ortogonal

Un método habitual para verificar si una matriz es ortogonal consiste en comprobar si la matriz multiplicada por su transpuesta es igual a la matriz identidad: Q^T Q = I.

Este enfoque pone a prueba directamente la definición fundamental de las matrices ortogonales y es eficiente desde el punto de vista computacional para matrices de cualquier tamaño. Cuando Q^T Q produce la matriz identidad, confirma que todas las columnas son ortonormales (de longitud unitaria y mutuamente ortogonales).

Para ello, podemos escribir una función sencilla en Python:

import numpy as np

def is_orthogonal(Q, tolerance=1e-10):
   """Check if Q^T * Q equals identity matrix"""
   # Matrix must be square
   if Q.shape[0] != Q.shape[1]:
       return False
  
   # Compute Q^T * Q
   QT_Q = np.dot(Q.T, Q)
   identity = np.eye(Q.shape[0])
  
   # Check if result is close to identity matrix
   return np.allclose(QT_Q, identity, atol=tolerance)

Podemos probar la función anterior con algunos ejemplos:

# Test a 2D rotation matrix
theta = np.pi/3  # 60 degrees
rotation_matrix = np.array([[np.cos(theta), -np.sin(theta)],
                          [np.sin(theta),  np.cos(theta)]])

print("Rotation matrix:")
print(rotation_matrix)
print("Is orthogonal:", is_orthogonal(rotation_matrix))

# Verify by computing Q^T * Q
QT_Q = np.dot(rotation_matrix.T, rotation_matrix)
print("Q^T * Q =")
print(QT_Q)

Como habíamos previsto, a continuación vemos el resultado que verifica la matriz ortogonal:

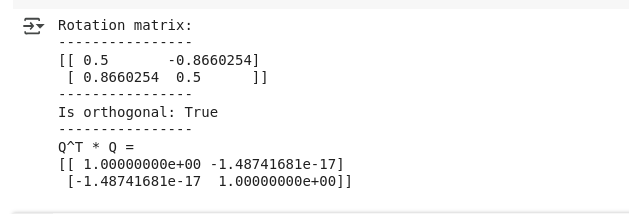Salida para matriz Salida para matriz ortogonal. Imagen del autor.

Además, también podemos verificar la función utilizando una matriz no ortogonal a continuación:

# Test with a non-orthogonal matrix
non_orthogonal = np.array([[1, 2], [3, 4]])
print("\nNon-orthogonal matrix:")
print(non_orthogonal)
print("Is orthogonal:", is_orthogonal(non_orthogonal))

La salida confirma lo mismo:

Salida para matriz no ortogonal. Imagen del autor.

El parámetro tolerancia tiene en cuenta la precisión aritmética en coma flotante. En la práctica, las matrices que son computacionalmente ortogonales (dentro de la precisión numérica) son aceptables para la mayoría de las aplicaciones, aunque no sean matemáticamente perfectas debido a errores de redondeo.

Conclusión

Este artículo explora las matrices ortogonales, matrices cuadradas especiales en las que la transpuesta es igual a la inversa, y sus notables propiedades que las hacen esenciales en la ciencia de datos y la computación numérica. Aprendimos cómo estas matrices conservan las distancias y los ángulos durante las transformaciones, examinamos sus aplicaciones en PCA, descomposición QR, gráficos por ordenador y procesamiento de señales, y descubrimos métodos prácticos para identificarlas utilizando implementaciones de Python.

Para profundizar tus conocimientos de álgebra lineal y sus aplicaciones en la ciencia de datos, considera la posibilidad de matricularte en nuestro curso de Álgebra Lineal para la Ciencia de Datos, donde explorarás conceptos matriciales más avanzados y sus implementaciones en escenarios del mundo real.