Orthogonale Matrix: Eine Erläuterung mit Beispielen und Code

Eine orthogonale Matrix ist eine quadratische Matrix, deren Spalten und Zeilen orthonormale Basen bilden, das heißt, sie sind orthogonal zueinander und haben eine Einheitslänge. Diese scheinbar einfache Eigenschaft birgt nützliche Fähigkeiten: Sie erhalten Abstände, Winkel und innere Produkte, wenn sie als lineare Transformationen angewendet werden. 

In diesem Artikel werden wir zunächst definieren, was eine orthogonale Matrix ist und ihre wichtigsten Eigenschaften und Beispiele untersuchen. Anschließend werden wir praktische Anwendungen untersuchen, orthogonale Matrizen mit orthonormalen Matrizen vergleichen und zeigen, wie man eine orthogonale Matrix in der Praxis identifiziert. Wenn du diese speziellen Matrizen verstehst, erhältst du einen Einblick in verschiedene Berechnungsmethoden, die in den Bereichen Datenwissenschaft, maschinelles Lernen und numerisches Rechnen eingesetzt werden.

Was ist eine orthogonale Matrix?

Eine orthogonale Matrix ist eine quadratische Matrix Q, deren Transponierte gleich ihrer Inversen ist:

Definition der orthogonalen Matrix. Bild vom Autor.

Wenn wir eine orthogonale Matrix mit ihrer Transponierten multiplizieren, erhalten wir die Identitätsmatrix:

Definition der orthogonalen Matrix. Bild vom Autor.

Aus geometrischer Sicht stellt eine orthogonale Matrix eine lineare Transformation dar, bei der die Länge von Vektoren und die Winkel zwischen ihnen erhalten bleiben. Zu diesen Transformationen gehören Drehungen, Spiegelungen oder Kombinationen dieser Operationen im n-dimensionalen Raum. Das bedeutet, dass sich bei der Multiplikation eines Vektors mit einer orthogonalen Matrix nur seine Ausrichtung ändert - nicht sein Betrag.

Eine weitere Möglichkeit, orthogonale Matrizen zu verstehen, ist ihre Struktur. In einer orthogonalen Matrix bilden alle Spalten eine orthonormale Menge von Vektoren - jede Spalte hat eine Einheitslänge (Norm = 1), und jedes Paar verschiedener Spalten ist orthogonal zueinander (ihr Punktprodukt ist gleich Null). Die gleiche Eigenschaft gilt für die Zeilen der Matrix.

Damit eine 2×2-Matrix orthogonal ist, müssen ihre Spalten zum Beispiel Einheitsvektoren sein, die senkrecht zueinander stehen. Dadurch entsteht eine starre geometrische Transformation, die die Struktur des Raums, auf dem sie wirkt, beibehält. Das macht orthogonale Matrizen zu grundlegenden Werkzeugen in Anwendungen, die geometrische Integrität erfordern.

Eigenschaften von orthogonalen Matrizen

Aufbauend auf der grundlegenden Definition erforschen wir als Nächstes die mathematischen und rechnerischen Eigenschaften, die orthogonale Matrizen in numerischen Anwendungen so wertvoll machen.

Determinante Klassifizierung 

Die Determinante einer orthogonalen Matrix ist immer entweder +1 oder -1, was diese Matrizen in zwei geometrische Kategorien einteilt:

• Wenn det(Q) = +1 ist, stellt die Matrix eine reine Rotation dar
• Wenn det(Q) = -1 ist, stellt die Matrix eine Spiegelung (oder eine Drehung kombiniert mit einer Spiegelung) dar

Diese Determinantenbeschränkung stellt sicher, dass orthogonale Transformationen das Volumen erhalten, indem sie den Raum neu ausrichten, anstatt ihn zu dehnen oder zu stauchen.

Konservierungseigenschaften 

Orthogonale Matrizen erhalten die geometrischen Beziehungen während der Transformation. 

Für jede orthogonale Matrix Q und Vektoren u und v:

• Die Vektornormen bleiben erhalten: |Qu| = ||u|
• Die inneren Produkte bleiben erhalten: (Qu) · (Qv) = u · v
• Winkel zwischen Vektoren bleiben unverändert

Diese Erhaltung geht über einzelne Vektoren hinaus - ganze geometrische Konfigurationen behalten ihre relative Struktur unter orthogonalen Transformationen bei.

Algebraische Eigenschaften 

Die Eigenwerte von orthogonalen Matrizen haben alle den Absolutwert 1. Bei reellen orthogonalen Matrizen sind diese Eigenwerte entweder 1, -1 oder erscheinen in komplex konjugierten Paaren auf dem Einheitskreis. Diese Einschränkung stellt sicher, dass die Umwandlung die Gesamtenergie des Systems weder verstärkt noch verringert.

Außerdem ist das Produkt zweier orthogonaler Matrizen immer orthogonal, was zu einer Schließungseigenschaft führt, die diese Matrizen für komplexe Transformationen und iterative Algorithmen gut geeignet macht.

Numerische Stabilität 

Aus rechnerischer Sicht besitzen orthogonale Matrizen außergewöhnliche numerische Eigenschaften. Sie haben eine Zustandszahl von 1, was sie für numerische Algorithmen extrem stabil macht. Das bedeutet, dass kleine Fehler bei der Eingabe während der Berechnung nicht vergrößert werden, was selbst bei komplexen Berechnungen zu zuverlässigen und genauen Ergebnissen führt. Diese Stabilität ist der Grund, warum orthogonale Matrizen in vielen numerischen Methoden bevorzugt werden und warum Algorithmen wie die QR-Zerlegung stark auf orthogonale Transformationen angewiesen sind.

Nachdem wir nun die Definition und die Eigenschaften, die orthogonale Matrizen auszeichnen, verstanden haben, schauen wir uns einige Beispiele an, um sie besser zu verstehen.

Beispiele für orthogonale Matrizen

Das Verständnis für orthogonale Matrizen wird klarer, wenn wir uns mit Beispielmatrizen beschäftigen.

Die Identitätsmatrix

Die einfachste orthogonale Matrix ist die Identitätsmatrix, die alle Vektoren unverändert lässt:

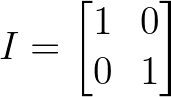
Identitätsmatrix. Bild vom Autor.

Die Identitätsmatrix ist zwar trivial, aber sie erfüllt unsere grundlegende Anforderung: I^T × I = I, was sie per Definition orthogonal macht.

2D-Drehungsmatrizen

Eines der intuitivsten Beispiele ist eine 2D-Rotationsmatrix, die Vektoren um den Winkel θ dreht:

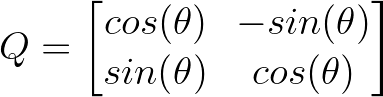
2D-Matrix. Bild vom Autor.

Eine Drehung um 45 Grad (π/4 Radiant) ergibt zum Beispiel:

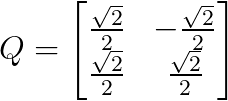
45 Grad gedrehte Matrix. Bild vom Autor.

Diese Matrix dreht jeden Vektor um 45 Grad gegen den Uhrzeigersinn und behält dabei seine Länge bei - ein perfektes Beispiel für eine orthogonale Transformation, die geometrische Eigenschaften bewahrt.

Reflexionsmatrizen

Reflexionsmatrizen spiegeln Vektoren in einer bestimmten Achse oder Ebene. Eine einfache Spiegelung an der x-Achse ist:

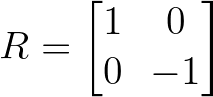
Beispiel für eine Reflexionsmatrix. Bild vom Autor.

Bei dieser Matrix bleibt die x-Koordinate unverändert, während die y-Koordinate negiert wird, wodurch die Vektoren an der horizontalen Achse gespiegelt werden.

3D-Transformationen

Indem wir sie auf drei Dimensionen ausdehnen, können wir Rotationsmatrizen für den 3D-Raum erstellen. Eine Drehung um die z-Achse um den Winkel θ sieht so aus:

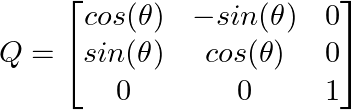
Durchführen von 3D-Transformationen. Bild vom Autor.

Beachte, dass die z-Koordinate erhalten bleibt, während die x- und y-Komponenten gedreht werden. Das zeigt, wie orthogonale Matrizen bestimmte Dimensionen selektiv transformieren können.

Jedes dieser Beispiele veranschaulicht das Grundprinzip orthogonaler Matrizen: Sie transformieren Vektoren unter Beibehaltung ihrer wesentlichen geometrischen Eigenschaften - die Längen bleiben unverändert und die Winkel zwischen den Vektoren bleiben erhalten.

Praktische Anwendungen von orthogonalen Matrizen

Orthogonale Matrizen werden aufgrund ihrer geometrischen und numerischen Eigenschaften in vielen verschiedenen Bereichen eingesetzt. 

Einige von ihnen sind:

• Prinzipielle Komponentenanalyse: Bei der PCAwerden orthogonale Matrizen verwendet, um Daten in ein neues Koordinatensystem zu transformieren, bei dem die größte Varianz entlang der ersten Koordinate liegt. Die Transformationsmatrix besteht aus orthogonalen Eigenvektoren, die die geometrische Struktur der Daten erhalten und gleichzeitig die Dimensionalität reduzieren.
• QR-Zerlegung: Jede Matrix kann unter in A = QR zerlegt werden, wobei Q orthogonal und R oberdreieckig ist. Diese Zerlegung ist grundlegend für die Lösung von linearen Systemen, Problemen der kleinsten Quadrate und Eigenwertberechnungen.
• Computergrafik und 3D-Transformationen Orthogonale Matrizen sind für 3D-Drehungen in der Computergrafik, Robotik und Computer Vision unerlässlich. Sie sorgen dafür, dass Objekte bei Drehungen ihre Form und Größe beibehalten und nicht verzerrt werden.
• Signalverarbeitung: Die Diskrete Cosinus-Transformation (DCT) und die Diskrete Fourier-Transformation verwenden orthogonale Matrizen, um Signale zwischen Zeit- und Frequenzbereich zu transformieren. Die JPEG-Kompression stützt sich stark auf die DCT, die orthogonale Transformationen verwendet.
• Quantencomputing: Quantengatter werden durch unitäre Matrizen dargestellt, die die komplexe Verallgemeinerung der orthogonalen Matrizen sind. Diese Transformationen erhalten die Wahrscheinlichkeitsamplituden in Quantensystemen.

Orthogonal vs. Orthonormale Matrizen

Die Begriffe orthogonale Matrix und orthonormale Matrix werden manchmal verwechselt, aber im Zusammenhang mit Matrizen wird nur die orthogonale Matrix verwendet, die bereits Orthonormalität impliziert. Die Verwirrung entsteht in der Regel, wenn die Terminologie von Vektormengen mit der von Matrizen vermischt wird.

Um die beiden zu vergleichen:

• Eine orthogonale Menge von Vektoren besteht aus Vektoren, die senkrecht zueinander stehen, aber nicht unbedingt die gleiche Länge haben.
• Eine orthonormale Menge besteht aus Vektoren, die senkrecht zueinander stehen und eine Einheitslänge haben (d.h. normalisiert sind).

Es entsteht also Verwirrung: Warum nennen wir es "orthogonal" und nicht "orthonormal"?

Obwohl die Spalten einer orthogonalen Matrix technisch gesehen orthonormal sind, ist der Begriff orthogonale Matrix der historisch etablierte Standardname in der linearen Algebra. Die Bezeichnung "orthonormale Matrix" ist überflüssig und wird in der formalen Mathematik selten, wenn überhaupt, verwendet.

Wenn wir sagen, dass eine Matrix orthogonal ist, meinen wir immer, dass ihre Spalten (und Zeilen) orthonormal sind - also senkrecht zueinander und von einheitlicher Länge. Ein separater Begriff wie "orthonormale Matrix" ist in diesem Zusammenhang nicht nötig.

Nachdem wir nun die Verwirrung mit den Namen geklärt haben, wollen wir herausfinden, wie man eine orthogonale Matrix identifiziert.

Wie man eine orthogonale Matrix identifiziert

Eine gängige Methode, um zu überprüfen, ob eine Matrix orthogonal ist, ist die Prüfung, ob die Matrix multipliziert mit ihrer Transponierten gleich der Identitätsmatrix ist: Q^T Q = I.

Dieser Ansatz testet direkt die grundlegende Definition orthogonaler Matrizen und ist rechnerisch effizient für Matrizen jeder Größe. Wenn Q^T Q die Identitätsmatrix ergibt, bestätigt dies, dass alle Spalten orthonormal sind (Einheitslänge und zueinander orthogonal).

Mit Python können wir eine einfache Funktion schreiben, die dies ermöglicht:

import numpy as np

def is_orthogonal(Q, tolerance=1e-10):
   """Check if Q^T * Q equals identity matrix"""
   # Matrix must be square
   if Q.shape[0] != Q.shape[1]:
       return False
  
   # Compute Q^T * Q
   QT_Q = np.dot(Q.T, Q)
   identity = np.eye(Q.shape[0])
  
   # Check if result is close to identity matrix
   return np.allclose(QT_Q, identity, atol=tolerance)

Wir können die obige Funktion anhand einiger Beispiele testen:

# Test a 2D rotation matrix
theta = np.pi/3  # 60 degrees
rotation_matrix = np.array([[np.cos(theta), -np.sin(theta)],
                          [np.sin(theta),  np.cos(theta)]])

print("Rotation matrix:")
print(rotation_matrix)
print("Is orthogonal:", is_orthogonal(rotation_matrix))

# Verify by computing Q^T * Q
QT_Q = np.dot(rotation_matrix.T, rotation_matrix)
print("Q^T * Q =")
print(QT_Q)

Wie erwartet, sehen wir unten die Ausgabe, die die orthogonale Matrix verifiziert:

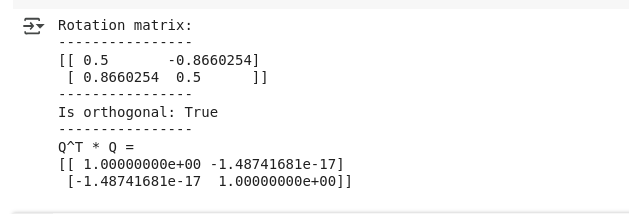Ausgabe für orthogonale Matrix. Bild vom Autor.

Außerdem können wir die Funktion auch mit einer nicht-orthogonalen Matrix überprüfen (siehe unten):

# Test with a non-orthogonal matrix
non_orthogonal = np.array([[1, 2], [3, 4]])
print("\nNon-orthogonal matrix:")
print(non_orthogonal)
print("Is orthogonal:", is_orthogonal(non_orthogonal))

Die Ausgabe bestätigt das Gleiche:

Ausgabe für nicht-orthogonale Matrix. Bild vom Autor.

Der Toleranzparameter berücksichtigt die Genauigkeit der Fließkomma-Arithmetik. In der Praxis sind Matrizen, die rechnerisch orthogonal sind (innerhalb der numerischen Genauigkeit), für die meisten Anwendungen akzeptabel, auch wenn sie aufgrund von Rundungsfehlern mathematisch nicht perfekt sind.

Fazit

Dieser Artikel befasst sich mit orthogonalen Matrizen, speziellen quadratischen Matrizen, bei denen die Transponierte gleich der Inversen ist, und ihren bemerkenswerten Eigenschaften, die sie in der Datenwissenschaft und im numerischen Rechnen unverzichtbar machen. Wir lernten, wie diese Matrizen Abstände und Winkel bei Transformationen bewahren, untersuchten ihre Anwendungen in PCA, QR-Zerlegung, Computergrafik und Signalverarbeitung und entdeckten praktische Methoden, um sie mit Python-Implementierungen zu identifizieren.

Wenn du deine Kenntnisse der linearen Algebra und ihrer Anwendungen in den Datenwissenschaften vertiefen möchtest, solltest du dich für unseren Kurs Lineare Algebra für Datenwissenschaften anmelden, in dem du fortgeschrittene Matrixkonzepte und ihre Anwendung in realen Szenarien kennenlernst.