Matrice orthogonale : Une explication avec des exemples et du code

Une matrice orthogonale est une matrice carrée dont les colonnes et les lignes forment des bases orthonormées, c'est-à-dire qu'elles sont orthogonales les unes par rapport aux autres et ont la même longueur. Cette propriété apparemment simple permet d'exploiter des capacités utiles : ils préservent les distances, les angles et les produits intérieurs lorsqu'ils sont appliqués en tant que transformations linéaires. 

Dans cet article, nous commencerons par définir ce qu'est une matrice orthogonale, puis nous examinerons ses principales propriétés et des exemples. Nous explorerons ensuite des applications pratiques, nous opposerons les matrices orthogonales aux matrices orthonormées et nous montrerons comment identifier une matrice orthogonale dans la pratique. En comprenant ces matrices spéciales, vous aurez un aperçu de diverses techniques de calcul utilisées dans la science des données, l'apprentissage automatique et le calcul numérique.

Qu'est-ce qu'une matrice orthogonale ?

Une matrice orthogonale est une matrice carrée Q dont la transposition est égale à son inverse :

Définition de la matrice orthogonale. Image par l'auteur.

Lorsque l'on multiplie une matrice orthogonale par sa transposée, on obtient la matrice identité :

Définition de la matrice orthogonale. Image par l'auteur.

D'un point de vue géométrique, une matrice orthogonale représente une transformation linéaire qui préserve la longueur des vecteurs et les angles entre eux. Ces transformations comprennent des rotations, des réflexions ou des combinaisons de ces opérations dans un espace à n dimensions. Cela signifie que lorsque l'on multiplie un vecteur par une matrice orthogonale, seule son orientation change, et non sa magnitude.

Une autre façon de comprendre les matrices orthogonales est de s'intéresser à leur structure. Dans une matrice orthogonale, toutes les colonnes forment un ensemble orthonormé de vecteurs - chaque colonne a une longueur unitaire (norme = 1) et chaque paire de colonnes différentes est orthogonale l'une par rapport à l'autre (leur produit en points est égal à zéro). La même propriété s'applique aux lignes de la matrice.

Pour qu'une matrice 2×2 soit orthogonale, par exemple, ses colonnes doivent être des vecteurs unitaires perpendiculaires les uns aux autres. Cela crée une transformation géométrique rigide qui préserve la structure de l'espace sur lequel elle opère, ce qui fait des matrices orthogonales des outils fondamentaux dans les applications nécessitant une intégrité géométrique.

Propriétés des matrices orthogonales

Sur la base de la définition fondamentale, nous explorerons ensuite les propriétés mathématiques et informatiques qui rendent les matrices orthogonales inestimables dans les applications numériques.

Classification des déterminants 

Le déterminant d'une matrice orthogonale est toujours soit +1, soit -1, ce qui classe ces matrices en deux catégories géométriques :

• Lorsque det(Q) = +1, la matrice représente une rotation pure
• Lorsque det(Q) = -1, la matrice représente une réflexion (ou une rotation combinée à une réflexion).

Cette contrainte de déterminant garantit que les transformations orthogonales préservent le volume, en réorientant l'espace plutôt qu'en l'étirant ou en le comprimant.

Propriétés de conservation 

Les matrices orthogonales maintiennent les relations géométriques au cours de la transformation. 

Pour toute matrice orthogonale Q et tout vecteur u et v :

• Les normes vectorielles sont préservées : ||Qu|| = ||u||
• Les produits intérieurs sont maintenus : (Qu) · (Qv) = u · v
• Les angles entre les vecteurs restent inchangés

Cette préservation s'étend au-delà des vecteurs individuels - des configurations géométriques entières conservent leur structure relative sous l'effet de transformations orthogonales.

Propriétés algébriques 

Les valeurs propres des matrices orthogonales ont toutes une valeur absolue égale à 1. Pour les matrices orthogonales réelles, ces valeurs propres sont soit 1, soit -1, soit apparaissent en paires conjuguées complexes sur le cercle unitaire. Cette contrainte garantit que la transformation n'amplifie ni ne diminue l'"énergie" globale du système.

En outre, le produit de deux matrices orthogonales est toujours orthogonal, ce qui crée une propriété de fermeture qui permet à ces matrices de bien se comporter dans le cadre de transformations complexes et d'algorithmes itératifs.

Stabilité numérique 

D'un point de vue informatique, les matrices orthogonales possèdent des propriétés numériques exceptionnelles. Ils ont un numéro de condition de 1, ce qui les rend extrêmement stables pour les algorithmes numériques. Cela signifie que les petites erreurs de saisie ne sont pas amplifiées pendant le calcul, ce qui permet d'obtenir des résultats fiables et précis, même dans le cas de calculs complexes. Cette stabilité est la raison pour laquelle les matrices orthogonales sont préférées dans de nombreuses méthodes numériques et que des algorithmes tels que la décomposition QR reposent fortement sur des transformations orthogonales.

Maintenant que nous avons compris la définition et les propriétés qui font la spécificité des matrices orthogonales, examinons quelques exemples pour mieux les comprendre.

Exemples de matrices orthogonales

La compréhension des matrices orthogonales devient plus claire lorsque nous explorons des exemples de matrices.

La matrice identité

La matrice orthogonale la plus élémentaire est la matrice identité, qui laisse tous les vecteurs inchangés :

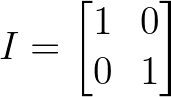
Matrice d'identité. Image par l'auteur.

Bien que triviale, la matrice identité répond à notre exigence fondamentale : I^T × I = I, ce qui le rend orthogonal par définition.

Matrices de rotation 2D

L'un des exemples les plus intuitifs est une matrice de rotation 2D qui fait pivoter les vecteurs d'un angle θ :

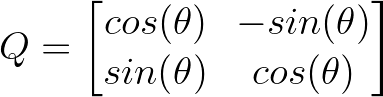
Matrice 2D. Image par l'auteur.

Par exemple, une rotation de 45 degrés (π/4 radians) nous donne

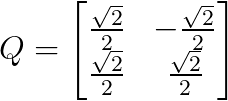
Matrice tournée à 45 degrés. Image par l'auteur.

Cette matrice fait pivoter n'importe quel vecteur de 45 degrés dans le sens inverse des aiguilles d'une montre tout en conservant sa longueur - un exemple parfait de transformation orthogonale préservant les propriétés géométriques.

Matrices de réflexion

Les matrices de réflexion retournent les vecteurs sur un axe ou un plan spécifique. Une simple réflexion sur l'axe des x est :

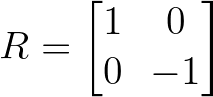
Exemple de matrice de réflexion. Image par l'auteur.

Cette matrice maintient la coordonnée x inchangée tout en annulant la coordonnée y, ce qui a pour effet d'inverser les vecteurs sur l'axe horizontal.

Transformations 3D

En passant à trois dimensions, nous pouvons créer des matrices de rotation pour l'espace 3D. Une rotation autour de l'axe z d'un angle θ se présente comme suit :

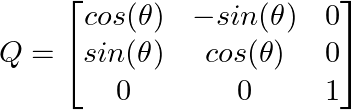
Effectuer des transformations 3D. Image par l'auteur.

Remarquez que cette méthode préserve la coordonnée z tout en faisant pivoter les composantes x et y, ce qui montre comment les matrices orthogonales peuvent transformer sélectivement des dimensions spécifiques.

Chacun de ces exemples illustre le principe fondamental des matrices orthogonales : elles transforment les vecteurs tout en préservant leurs propriétés géométriques essentielles - les longueurs restent inchangées et les angles entre les vecteurs sont conservés.

Applications pratiques des matrices orthogonales

Les matrices orthogonales sont largement utilisées dans divers domaines en raison de leurs propriétés géométriques et numériques. 

En voici quelques-unes :

• Analyse en composantes principales: L'ACP utilisez des matrices orthogonales pour transformer les données dans un nouveau système de coordonnées où la plus grande variance se situe le long de la première coordonnée. La matrice de transformation se compose de vecteurs propres orthogonaux qui préservent la structure géométrique des données tout en réduisant la dimensionnalité.
• Décomposition QR: Toute matrice peut être décomposée à l'adresse sous la forme A = QR, où Q est orthogonal et R est triangulaire supérieur. Cette décomposition est fondamentale pour résoudre les systèmes linéaires, les problèmes de moindres carrés et les calculs de valeurs propres.
• Infographie et transformations 3D Les matrices orthogonales sont essentielles pour les rotations 3D dans l'infographie, la robotique et la vision par ordinateur. Ils garantissent que les objets conservent leur forme et leur taille pendant les rotations, évitant ainsi les distorsions.
• Traitement du signal: La transformée en cosinus discrète (DCT) et la transformée de Fourier discrètete utilisent des matrices orthogonales pour transformer les signaux entre les domaines du temps et de la fréquence. La compression JPEG s'appuie fortement sur la DCT, qui utilise des transformations orthogonales.
• L'informatique quantique : Les portes quantiques sont représentées par des matrices unitaires, qui sont la généralisation complexe des matrices orthogonales. Ces transformations préservent les amplitudes de probabilité dans les systèmes quantiques.

Orthogonal vs. Matrices orthonormées

Les termes matrice orthogonale et matrice orthonormée sont parfois confondus, mais dans le contexte des matrices, seule la matrice orthogonale est utilisée, et elle implique déjà l'orthonormalité. La confusion survient généralement lorsque l'on mélange la terminologie des ensembles vectoriels avec celle des matrices.

Pour les opposer l'un à l'autre :

• Un ensemble orthogonal de vecteurs est constitué de vecteurs qui sont mutuellement perpendiculaires, mais qui ne sont pas nécessairement de longueur unitaire.
• Un ensemble ensemble orthonormé est constitué de vecteurs qui sont à la fois mutuellement perpendiculaires et de longueur unitaire (c'est-à-dire normalisés).

D'où la confusion : pourquoi parle-t-on d'"orthogonal" et non d'"orthonormé" ?

Bien que les colonnes d'une matrice orthogonale soient techniquement orthonormées, le terme de matrice orthogonale est le nom standard, historiquement établi en algèbre linéaire. L'appellation "matrice orthonormée" est redondante et rarement, voire jamais, utilisée en mathématiques formelles.

Lorsque nous disons qu'une matrice est orthogonale, nous voulons toujours dire que ses colonnes (et ses lignes) sont orthonormées, c'est-à-dire qu'elles sont mutuellement perpendiculaires et de longueur unitaire. Il n'est pas nécessaire d'utiliser un terme distinct comme "matrice orthonormée" dans ce contexte.

Maintenant que nous avons dissipé la confusion avec les noms, voyons comment identifier une matrice orthogonale.

Comment identifier une matrice orthogonale

Une méthode courante pour vérifier si une matrice est orthogonale consiste à vérifier si la matrice multipliée par sa transposée est égale à la matrice identité : Q^T Q = I.

Cette approche teste directement la définition fondamentale des matrices orthogonales et est efficace en termes de calcul pour les matrices de toute taille. Lorsque Q^T Q produit la matrice identité, cela confirme que toutes les colonnes sont orthonormées (longueur unitaire et orthogonales entre elles).

Pour ce faire, nous pouvons écrire une fonction simple en Python :

import numpy as np

def is_orthogonal(Q, tolerance=1e-10):
   """Check if Q^T * Q equals identity matrix"""
   # Matrix must be square
   if Q.shape[0] != Q.shape[1]:
       return False
  
   # Compute Q^T * Q
   QT_Q = np.dot(Q.T, Q)
   identity = np.eye(Q.shape[0])
  
   # Check if result is close to identity matrix
   return np.allclose(QT_Q, identity, atol=tolerance)

Nous pouvons tester la fonction ci-dessus à l'aide de quelques exemples :

# Test a 2D rotation matrix
theta = np.pi/3  # 60 degrees
rotation_matrix = np.array([[np.cos(theta), -np.sin(theta)],
                          [np.sin(theta),  np.cos(theta)]])

print("Rotation matrix:")
print(rotation_matrix)
print("Is orthogonal:", is_orthogonal(rotation_matrix))

# Verify by computing Q^T * Q
QT_Q = np.dot(rotation_matrix.T, rotation_matrix)
print("Q^T * Q =")
print(QT_Q)

Comme prévu, le résultat vérifiant la matrice orthogonale apparaît ci-dessous :

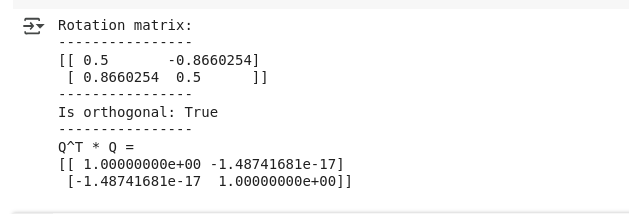Sortie pour la matrice orthogonale. Image par l'auteur.

En outre, nous pouvons également vérifier la fonction à l'aide d'une matrice non orthogonale ci-dessous :

# Test with a non-orthogonal matrix
non_orthogonal = np.array([[1, 2], [3, 4]])
print("\nNon-orthogonal matrix:")
print(non_orthogonal)
print("Is orthogonal:", is_orthogonal(non_orthogonal))

La sortie confirme la même chose :

Sortie pour une matrice non orthogonale. Image par l'auteur.

Le paramètre de tolérance tient compte de la précision arithmétique en virgule flottante. En pratique, les matrices qui sont orthogonales d'un point de vue informatique (dans les limites de la précision numérique) sont acceptables pour la plupart des applications, même si elles ne sont pas parfaites d'un point de vue mathématique en raison d'erreurs d'arrondi.

Conclusion

Cet article explore les matrices orthogonales, des matrices carrées spéciales où la transposée est égale à l'inverse, et leurs propriétés remarquables qui les rendent essentielles dans la science des données et le calcul numérique. Nous avons appris comment ces matrices préservent les distances et les angles au cours des transformations, examiné leurs applications dans l'ACP, la décomposition QR, l'infographie et le traitement du signal, et découvert des méthodes pratiques pour les identifier à l'aide d'implémentations Python.

Pour approfondir votre connaissance de l'algèbre linéaire et de ses applications en science des données, envisagez de vous inscrire à notre cours d' algèbre linéaire pour la science des données, où vous explorerez des concepts matriciels plus avancés et leurs implémentations dans des scénarios du monde réel.