Matriz ortogonal: Uma explicação com exemplos e código

Uma matriz ortogonal é uma matriz quadrada cujas colunas e linhas formam bases ortonormais, o que significa que são ortogonais entre si e têm comprimento unitário. Essa propriedade aparentemente simples revela recursos úteis: eles preservam distâncias, ângulos e produtos internos quando aplicados como transformações lineares. 

Neste artigo, primeiro definiremos o que é uma matriz ortogonal e examinaremos suas principais propriedades e exemplos. Em seguida, exploraremos as aplicações práticas, compararemos as matrizes ortogonais com as ortonormais e demonstraremos como identificar uma matriz ortogonal na prática. Ao compreender essas matrizes especiais, você terá uma visão de várias técnicas computacionais usadas em ciência de dados, machine learning e computação numérica.

O que é uma matriz ortogonal?

Uma matriz ortogonal é uma matriz quadrada Q cuja transposição é igual à sua inversa:

Definição de matriz ortogonal. Imagem do autor.

Quando multiplicamos uma matriz ortogonal por sua transposição, obtemos a matriz identidade:

Definição de matriz ortogonal. Imagem do autor.

De uma perspectiva geométrica, uma matriz ortogonal representa uma transformação linear que preserva o comprimento dos vetores e os ângulos entre eles. Essas transformações incluem rotações, reflexões ou combinações dessas operações em um espaço n-dimensional. Isso significa que, quando multiplicamos um vetor por uma matriz ortogonal, apenas sua orientação muda, não sua magnitude.

Outra maneira de entender as matrizes ortogonais é por meio de sua estrutura. Em uma matriz ortogonal, todas as colunas formam um conjunto ortonormal de vetores - cada coluna tem comprimento unitário (norma = 1) e cada par de colunas diferentes é ortogonal entre si (seu produto escalar é igual a zero). A mesma propriedade se aplica às linhas da matriz.

Para que uma matriz 2×2 seja ortogonal, por exemplo, suas colunas devem ser vetores unitários perpendiculares entre si. Isso cria uma transformação geométrica rígida que preserva a estrutura do espaço em que opera, tornando as matrizes ortogonais ferramentas fundamentais em aplicativos que exigem integridade geométrica.

Propriedades das matrizes ortogonais

Com base na definição básica, a seguir exploraremos as propriedades matemáticas e computacionais que tornam as matrizes ortogonais inestimáveis em aplicações numéricas.

Classificação determinante 

O determinante de uma matriz ortogonal é sempre +1 ou -1, o que classifica essas matrizes em duas categorias geométricas:

• Quando det(Q) = +1, a matriz representa uma rotação pura
• Quando det(Q) = -1, a matriz representa uma reflexão (ou uma rotação combinada com uma reflexão)

Essa restrição determinante garante que as transformações ortogonais preservem o volume, reorientando o espaço em vez de esticá-lo ou comprimi-lo.

Propriedades de preservação 

As matrizes ortogonais mantêm as relações geométricas durante a transformação. 

Para qualquer matriz ortogonal Q e vetores u e v:

• As normas vetoriais são preservadas: ||Qu|| = ||u||
• Os produtos internos são mantidos: (Qu) - (Qv) = u - v
• Os ângulos entre os vetores permanecem inalterados

Essa preservação vai além dos vetores individuais - configurações geométricas inteiras mantêm sua estrutura relativa sob transformações ortogonais.

Propriedades algébricas 

Os valores próprios das matrizes ortogonais têm valor absoluto igual a 1. Para matrizes ortogonais reais, esses valores próprios são 1, -1 ou aparecem em pares conjugados complexos no círculo unitário. Essa restrição garante que a transformação não amplie nem diminua a "energia" geral do sistema.

Além disso, o produto de duas matrizes ortogonais é sempre ortogonal, criando uma propriedade de fechamento que torna essas matrizes bem comportadas para transformações complexas e algoritmos iterativos.

Estabilidade numérica 

Do ponto de vista computacional, as matrizes ortogonais possuem propriedades numéricas excepcionais. Eles têm um número de condição de 1, o que os torna extremamente estáveis para algoritmos numéricos. Isso significa que pequenos erros na entrada não são ampliados durante o cálculo, levando a resultados confiáveis e precisos, mesmo em cálculos complexos. Essa estabilidade é a razão pela qual as matrizes ortogonais são preferidas em muitos métodos numéricos e por que algoritmos como a decomposição QR dependem muito de transformações ortogonais.

Agora que você entendeu a definição e as propriedades que tornam as matrizes ortogonais especiais, vamos dar uma olhada em alguns exemplos para entendê-las melhor.

Exemplos de matrizes ortogonais

A compreensão das matrizes ortogonais fica mais clara quando exploramos exemplos de matrizes.

A matriz identidade

A matriz ortogonal mais básica é a matriz identidade, que deixa todos os vetores inalterados:

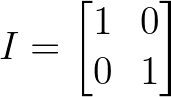
Matriz de identidade. Imagem do autor.

Embora trivial, a matriz identidade satisfaz nosso requisito fundamental: I^T × I = I, tornando-o ortogonal por definição.

Matrizes de rotação 2D

Um dos exemplos mais intuitivos é uma matriz de rotação 2D que gira os vetores em um ângulo θ:

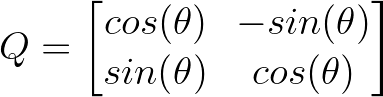
Matriz 2D. Imagem do autor.

Por exemplo, ao girar 45 graus (π/4 radianos), você obtém:

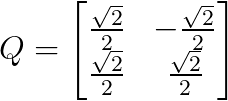
Matriz com rotação de 45 graus. Imagem do autor.

Essa matriz gira qualquer vetor em 45 graus no sentido anti-horário, preservando seu comprimento - um exemplo perfeito de uma transformação ortogonal que preserva as propriedades geométricas.

Matrizes de reflexão

As matrizes de reflexão invertem os vetores em um eixo ou plano específico. Uma reflexão simples no eixo x é:

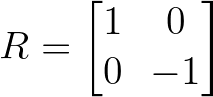
Exemplo de matriz de reflexão. Imagem do autor.

Essa matriz mantém a coordenada x inalterada e nega a coordenada y, espelhando efetivamente os vetores no eixo horizontal.

Transformações 3D

Estendendo para três dimensões, podemos criar matrizes de rotação para o espaço 3D. Uma rotação em torno do eixo z em um ângulo θ tem a seguinte aparência:

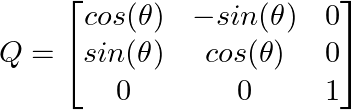
Realização de transformações em 3D. Imagem do autor.

Observe como isso preserva a coordenada z enquanto gira os componentes x e y, demonstrando como as matrizes ortogonais podem transformar seletivamente dimensões específicas.

Cada um desses exemplos demonstra o princípio central das matrizes ortogonais: elas transformam os vetores enquanto preservam suas propriedades geométricas essenciais - os comprimentos permanecem inalterados e os ângulos entre os vetores são mantidos.

Aplicações práticas de matrizes ortogonais

As matrizes ortogonais são amplamente utilizadas em vários domínios devido às suas propriedades geométricas e numéricas. 

Alguns deles incluem:

• Análise de componentes principais: A PCA utiliza matrizes ortogonais para transformar dados em um novo sistema de coordenadas em que a maior variação está ao longo da primeira coordenada. A matriz de transformação consiste em vetores próprios ortogonais que preservam a estrutura geométrica dos dados e, ao mesmo tempo, reduzem a dimensionalidade.
• Decomposição QR: Toda matriz pode ser decomposta como A = QR, em que Q é ortogonal e R é triangular superior. Essa decomposição é fundamental na solução de sistemas lineares, problemas de mínimos quadrados e cálculos de valores próprios.
• Computação gráfica e transformações 3D As matrizes ortogonais são essenciais para rotações 3D em computação gráfica, robótica e visão computacional. Eles garantem que os objetos mantenham sua forma e tamanho durante as rotações, evitando distorções.
• Processamento de sinais: A Transformada Discreta de Cosseno (DCT) e a Transformada Discreta de Fourier usam matrizes ortogonais para transformar sinais entre os domínios de tempo e frequência. A compactação JPEG depende muito da DCT, que usa transformações ortogonais.
• Computação quântica: As portas quânticas são representadas por matrizes unitárias, que são a generalização complexa das matrizes ortogonais. Essas transformações preservam as amplitudes de probabilidade em sistemas quânticos.

Ortogonal versus ortogonal. Matrizes ortonormais

Às vezes, os termos matriz ortogonal e matriz ortonormal são confundidos, mas, no contexto das matrizes, apenas a matriz ortogonal é usada, e ela já implica ortonormalidade. A confusão geralmente surge quando você mistura a terminologia de conjuntos de vetores com a de matrizes.

Para contrastar os dois:

• Um conjunto ortogonal de vetores consiste em vetores que são mutuamente perpendiculares, mas não necessariamente de comprimento unitário.
• Um conjunto ortonormal consiste em vetores que são mutuamente perpendiculares e de comprimento unitário (ou seja, normalizados).

Então, surge a confusão: por que chamamos isso de "ortogonal" e não de "ortonormal"?

Embora as colunas de uma matriz ortogonal sejam tecnicamente ortonormais, o termo matriz ortogonal é o nome padrão e historicamente estabelecido na álgebra linear. O rótulo "matriz ortonormal" é redundante e raramente, ou nunca, usado na matemática formal.

Quando dizemos que uma matriz é ortogonal, sempre queremos dizer que suas colunas (e linhas) são ortonormais - mutuamente perpendiculares e de comprimento unitário. Não há necessidade de um termo separado como "matriz ortonormal" nesse contexto.

Agora que esclarecemos a confusão com os nomes, vamos descobrir como identificar uma matriz ortogonal.

Como identificar uma matriz ortogonal

Um método comum para verificar se uma matriz é ortogonal é verificar se a matriz multiplicada por sua transposição é igual à matriz identidade: Q^T Q = I.

Essa abordagem testa diretamente a definição fundamental de matrizes ortogonais e é computacionalmente eficiente para matrizes de qualquer tamanho. Quando Q^T Q produz a matriz identidade, isso confirma que todas as colunas são ortonormais (comprimento unitário e mutuamente ortogonais).

Você pode escrever uma função simples usando Python para fazer isso:

import numpy as np

def is_orthogonal(Q, tolerance=1e-10):
   """Check if Q^T * Q equals identity matrix"""
   # Matrix must be square
   if Q.shape[0] != Q.shape[1]:
       return False
  
   # Compute Q^T * Q
   QT_Q = np.dot(Q.T, Q)
   identity = np.eye(Q.shape[0])
  
   # Check if result is close to identity matrix
   return np.allclose(QT_Q, identity, atol=tolerance)

Podemos testar a função acima usando alguns exemplos:

# Test a 2D rotation matrix
theta = np.pi/3  # 60 degrees
rotation_matrix = np.array([[np.cos(theta), -np.sin(theta)],
                          [np.sin(theta),  np.cos(theta)]])

print("Rotation matrix:")
print(rotation_matrix)
print("Is orthogonal:", is_orthogonal(rotation_matrix))

# Verify by computing Q^T * Q
QT_Q = np.dot(rotation_matrix.T, rotation_matrix)
print("Q^T * Q =")
print(QT_Q)

Conforme previsto, você verá o resultado da verificação da matriz ortogonal abaixo:

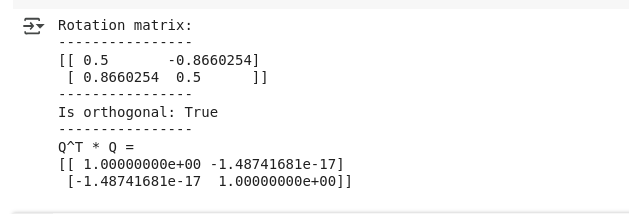Saída para matriz ortogonal. Imagem do autor.

Além disso, também podemos verificar a função usando uma matriz não ortogonal abaixo:

# Test with a non-orthogonal matrix
non_orthogonal = np.array([[1, 2], [3, 4]])
print("\nNon-orthogonal matrix:")
print(non_orthogonal)
print("Is orthogonal:", is_orthogonal(non_orthogonal))

O resultado confirma o mesmo:

Saída para matriz não ortogonal. Imagem do autor.

O parâmetro de tolerância leva em conta a precisão aritmética de ponto flutuante. Na prática, as matrizes que são computacionalmente ortogonais (dentro da precisão numérica) são aceitáveis para a maioria das aplicações, mesmo que não sejam matematicamente perfeitas devido a erros de arredondamento.

Conclusão

Este artigo explorou as matrizes ortogonais, matrizes quadradas especiais em que a transposição é igual à inversa, e suas propriedades notáveis que as tornam essenciais na ciência de dados e na computação numérica. Aprendemos como essas matrizes preservam as distâncias e os ângulos durante as transformações, examinamos suas aplicações em PCA, decomposição QR, computação gráfica e processamento de sinais e descobrimos métodos práticos para identificá-las usando implementações em Python.

Para aprofundar seu conhecimento sobre álgebra linear e suas aplicações na ciência de dados, considere a possibilidade de se inscrever em nosso curso Álgebra linear para ciência de dados, no qual você explorará conceitos de matriz mais avançados e suas implementações em cenários do mundo real.