QR Decomposition in Machine Learning: A Detailed Guide

QR decomposition is a fundamental matrix factorization technique widely used in various fields of data science and machine learning. Its ability to break down complex matrices into simpler pieces makes it a much-needed method for solving linear algebra problems and improving the stability of algorithms.

Whether you're performing ordinary least squares linear regression or building recommendation engines in Python or PySpark, understanding QR decomposition can significantly add to your ability to work with large datasets and complex mathematical models. 

What is QR Decomposition?

When you factorize, or decompose, a matrix, you express that matrix as the product of two or more matrices. In other words, matrix factorization allows you to break down a matrix into simpler components, which, when multiplied together using matrix multiplication, will reconstruct the original matrix. We care about matrix factorization because it simplifies many linear algebra problems, making them easier to solve. 

A QR decomposition is a specific kind of matrix factorization technique that is used to factorize a matrix into the product of an orthogonal matrix Q and an upper triangular matrix R. The equation we commonly see is A = QR. 

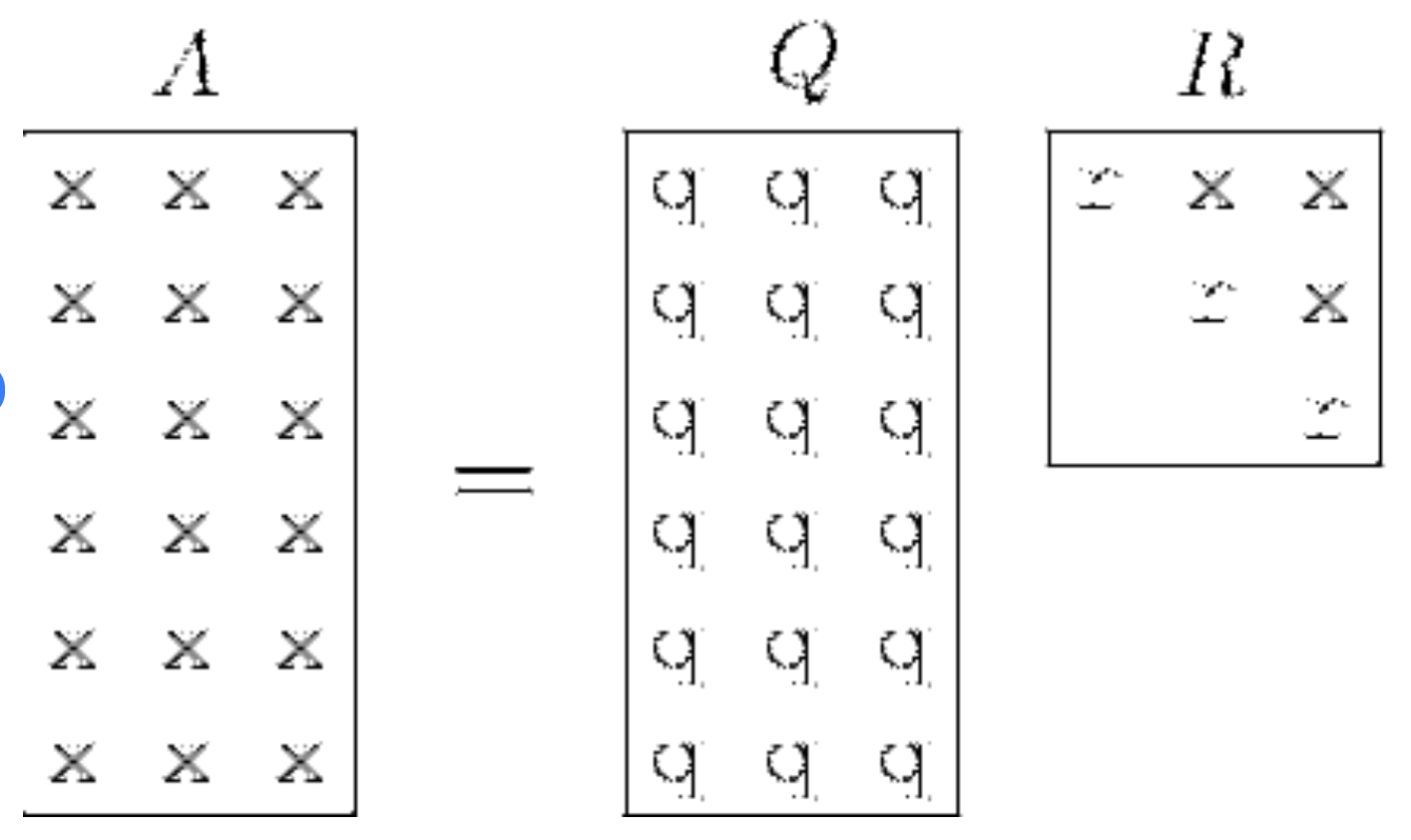
QR decomposition visualized. Source: ResearchGate

In order to understand QR decomposition, you have to appreciate that in linear algebra, multiplication of matrices doesn't follow the same intuitive rules as scalar multiplication. To be specific, multiplying matrices isn't commutative, meaning AB ≠ BA in general, and therefore, the notion of "reverse" is more complex.

What are the Q and R Matrices?

Let’s take a look at the two important matrices, Q and R.

Orthogonal matrix Q

An orthogonal matrix Q is characterized by the property that its transpose is also its inverse, which is mathematically represented as Q^TQ = QQ^T  =  I, where I is the identity matrix. Transposing, for context, means flipping the matrix over its diagonal.

An orthogonal matrix is also characterized by the fact that its columns form an orthonormal basis. This means two things: For one, the columns are orthogonal, which is to say that the dot product of any pair of distinct columns in the matrix is zero. And two, each column has a magnitude, or unit length, of one.

Orthogonal matrices are good to work with because they preserve the lengths of vectors and their dot products. So, if you have a vector and you multiply it by an orthogonal matrix, the length of that vector stays the same. Also, if you have two vectors and you multiply them both by the same orthogonal matrix, the dot product between them also stays the same. Finally, because orthogonal matrices preserve lengths and dot products, they don't distort the geometric properties of the vectors after our transformation. That is, if two vectors are perpendicular before the transformation, they will remain perpendicular after applying the orthogonal matrix. 

Upper triangular matrix R

An upper triangular matrix R is a type of matrix where all the elements below the main diagonal are zero. This form simplifies matrix equations and is particularly useful in solving systems of linear equations through back substitution or another method. We could also say that, in QR decomposition, R represents the component that captures the original matrix's magnitude and orientation.

Ways to Perform QR Decomposition

Let’s take a quick look at some of the different ways to perform QR decomposition.

The Gram Schmidt process 

The Gram Schmidt process is an algorithm that is used to systematically convert a set of linearly independent vectors into an orthonormal set. This process is used specifically for constructing the Q matrix in our QR decomposition and, after we have Q, we can derive R. 

Givens rotations

Givens rotations is another method to help with QR decomposition. With Givens rotations, a series of plane rotations is applied to introduce zeros below the diagonal of the matrix A. Each rotation acts on a pair of coordinates, preserving the length of the vector while transforming the matrix into an upper triangular form. This method is efficient for sparse matrices, as it only modifies a small portion of the matrix at each step.

Householder reflections

Householder reflections are a more general technique that uses reflection matrices, known as Householder matrices, to systematically eliminate the sub-diagonal elements of matrix A. Each Householder matrix reflects a vector across a plane orthogonal to the vector chosen to zero out a column below the diagonal. The result is an orthogonal matrix Q, and an upper triangular matrix R. Householder reflections are particularly good for dense matrices because of their numerical stability.

Implementing QR Decomposition in R

In this section, we will practice QR decomposition in R by utilizing both the built-in qr() function for a quick implementation and then walking through the process from scratch using the Gram Schmidt process to build our intuition. Let’s start by creating matrix_A, which we will use in both sections.  

matrix_A <- matrix(c(21, 21, 22.8, 21.4, 18.7, 18.1, 14.3, 24.4, 22.8, 19.2, 17.8, 16.4, 17.3, 15.2, 10.4, 10.4, 14.7, 32.4, 30.4, 33.9, 21.5, 15.5, 15.2, 13.3, 19.2, 27.3, 26, 30.4, 15.8, 19.7, 15, 21.4, 
              2.62, 2.875, 2.32, 3.215, 3.44, 3.46, 3.57, 3.19, 3.15, 3.44, 3.44, 4.07, 3.73, 3.78, 5.25, 5.424, 5.345, 2.2, 1.615, 1.835, 2.465, 3.52, 3.435, 3.84, 3.845, 1.935, 2.14, 1.513, 3.17, 2.77, 3.57, 2.78, 
              110, 110, 93, 110, 175, 105, 245, 62, 95, 123, 123, 180, 180, 180, 205, 215, 230, 66, 52, 65, 97, 150, 150, 245, 175, 66, 91, 113, 264, 175, 335, 109), 
            nrow = 32, ncol = 3, byrow = FALSE)

# Add column names
colnames(matrix_A) <- c("column_1", "column_2", "column_3")

QR decomposition using the qr() function

We can do this factorization in one step with the qr() function. We assign the result to a qr_decomp object, which is a list containing the QR decomposition. 

# Perform and Display the QR decomposition
(qr_decomp <- qr(matrix_A))

When we access the rank component of the QR decomposition object we can see the number of linearly independent columns in our decomposed matrix. The output indicates that the matrix has a rank of three, meaning there are three linearly independent columns, which is what we expect. When we access the pivot component, we can see information about the permutation of columns used during the decomposition process. The output indicates that the columns of the matrix were not permuted during the decomposition, as the pivot indices match the original column order.

qr_decomp$rank
qr_decomp$pivot

[1] 3
[1] 1 2 3

As a next step, we can access the Q matrix and the R matrix using the qr.Q() and qr.R() functions, respectively. We can see in the output that the Q matrix is rectangular and the R matrix is square with zeros below the diagonal. 

# Extract and Display the Q and R matrices
(Q_matrix <- qr.Q(qr_decomp))
(R_matrix <- qr.R(qr_decomp))

           [,1]         [,2]         [,3]
 [1,] -0.17721481  0.023462372 -0.015872336
 [2,] -0.17721481 -0.001889138 -0.060272525
 [3,] -0.19240465  0.077625112 -0.019039920
 [4,] -0.18059033 -0.030282834 -0.118470211
 [5,] -0.15780557 -0.089157964  0.064671266
 [6,] -0.15274229 -0.099258795 -0.187022354
 [7,] -0.12067485 -0.161573766  0.277715036
 [8,] -0.20590673  0.012764996 -0.275768785
 [9,] -0.19240465 -0.004891570 -0.156509401
[10,] -0.16202497 -0.082397566 -0.117343880
[11,] -0.15021065 -0.101326680 -0.120852866
[12,] -0.13839633 -0.182888939 -0.033166125
[13,] -0.14599125 -0.136918208  0.028289904
[14,] -0.12826977 -0.170282764  0.014320506
[15,] -0.08776353 -0.381326588 -0.165554550
[16,] -0.08776353 -0.398625266 -0.160607236
[17,] -0.12405037 -0.332631845 -0.083208412
[18,] -0.27341714  0.219354877 -0.069242665
[19,] -0.25653954  0.250472633 -0.021737724
[20,] -0.28607534  0.275923528 -0.005454217
[21,] -0.18143421  0.045632512 -0.033447865
[22,] -0.13080141 -0.140377926 -0.045388530
[23,] -0.12826977 -0.135983661 -0.031340393
[24,] -0.11223605 -0.201937338  0.228196652
[25,] -0.16202497 -0.122661730 -0.004593473
[26,] -0.23037925  0.176744505 -0.035884026
[27,] -0.21940881  0.138786843  0.013273146
[28,] -0.25653954  0.260613237  0.211010230
[29,] -0.13333305 -0.101525496  0.418085457
[30,] -0.16624437 -0.009027316  0.183837006
[31,] -0.12658201 -0.152109209  0.596664759
[32,] -0.18059033  0.012963861 -0.046253102

      column_1  column_2  column_3
[1,] -118.5003 -16.11602 -711.9200
[2,]    0.0000 -10.05857 -496.9319
[3,]    0.0000   0.00000  283.7369

As a final step, because we are curious, we can check which method the qr() function uses for decomposition. 

?qr

We can see the following as part of the output:  

The function computes the QR decomposition of a matrix using the LINPACK or LAPACK routine dgeqrf.

If we were to check FORTRAN documentation, we would see that dgeqrf is a LAPACK routine that uses Householder transformations. 

QR decomposition using the Gram Schmidt process

Let’s try to understand what is happening with the qr() function by recreating not the same implementation but a similar idea ourselves by following the Gram Schmidt process and thinking. The purpose of this exercise is not to recreate an exact method but rather to build our understanding.

Constructing the Q matrix

In order to start creating our Q matrix using the Gram Schmidt process, we need to normalize the first column of the subset data to obtain the first column of Q. The goal here is to transform our set of vectors in matrix A into a new set vectors with a unit length of one, and to make sure these vectors are orthogonal to each other.

To find the first column of Q, we extract the first column of A, calculate the Euclidean norm, then perform normalization.

To review, the Euclidean norm is a measure of the length or magnitude of a vector in Euclidean space. We consider the distance from the origin to the end of the vector when considering each vector element as a coordinate in multi-dimensional space. For a vector v = [v1​,v2​,…,vn​], its Euclidean norm is calculated in the following way:

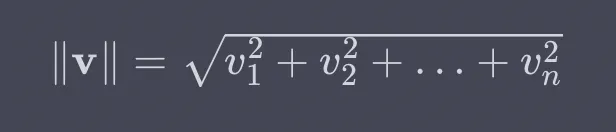
So, to implement in R, we square each column, take the sum, then the square root, and, finally, we normalize.

# Extract the first column of the subset data
col_1 <- matrix_A[, 1]

# Calculate the Euclidean norm of the first column
norm_col_1 <- sqrt(sum(col_1^2))

# Normalize and display the first column to get the first column of Q
(q1 <- col_1 / norm_col_1)

The second thing we need to review from linear algebra is the concept of a projection. A projection refers to a mathematical operation that projects a vector onto a subspace. The subspace can be thought of as a lower-dimensional space within the larger vector space. The resulting projection is a vector that lies within the subspace and is closest to the original vector being projected, which is also orthogonal to the subspace. 

Let’s try to visualize with the following graph, where the projection p is the point closest to a from b, which must be perpendicular to b.

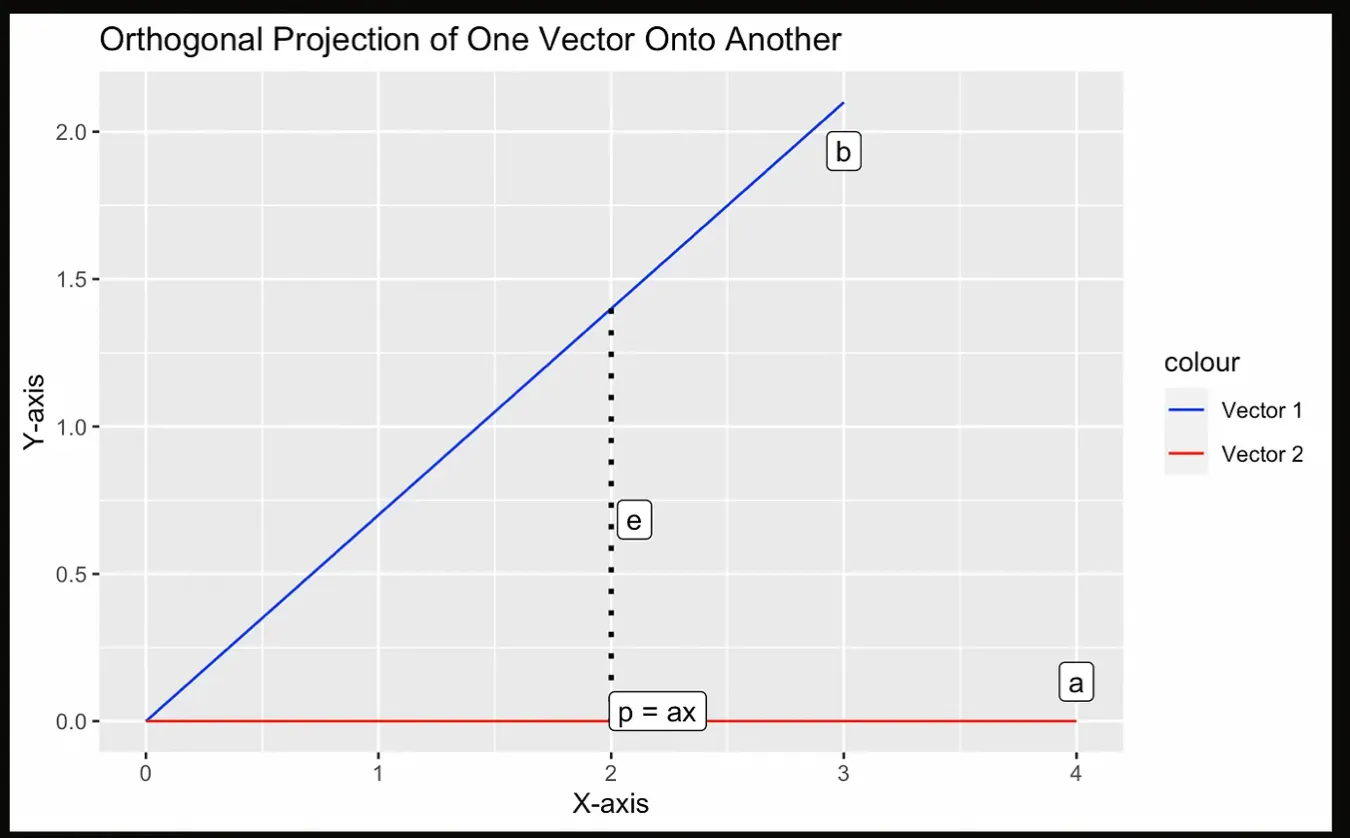
Illustration of a projection. Image by Author.

In the next step of QR factorization, we calculate the second orthogonal vector by first calculating the projection of the second column of A onto the first column of Q, and then subtracting that result from the second column of A. The resulting vector will be orthogonal to the first vector. As a final step, we normalize this vector to obtain the second column of Q.

Let’s review the equation for a projection. The projection is the matrix that is a times a-transpose over the scalar value that is a-transpose times a, multiplied by b.

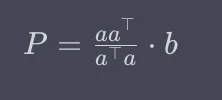
Or, alternatively:

We might be wondering: How are these two methods the same? Well, when we look at the first equation above, the part to the left of b computes a matrix that essentially captures the direction defined by vector a and the scaling factor for that direction. This is similar to calculating the unit vector of a in the dot product method. 

The following R code calculates the projection of the vector col_2 onto the vector q1 using the dot product method.

# Extract the second column of the subset data
col_2 <- matrix_A[, 2]

# Calculate the projection of col_2 onto q1
projection_col_2_q1 <- sum(col_2 * q1) * q1

# Calculate the second orthogonal vector
v2 <- col_2 - projection_col_2_q1

# Calculate the Euclidean norm of the second orthogonal vector
norm_v2 <- sqrt(sum(v2^2))

# Normalize the second orthogonal vector to get the second column of Q
q2 <- v2 / norm_v2

As we can see in the code above, constructing the second orthogonal vector and the corresponding column of the matrix Q involves a process of projection, subtraction, and normalization. The basic steps are similar to creating the first column of Q, but they are a bit different and slightly more involved: We first extract the second column of A; we then create a projection onto the first vector of Q; we then subtract the projection from the second column of A; we then perform normalization; finally, we create the second column of Q.

We can repeat this second step for q3 all the way to the last column. In our case, the orthogonal vectors q1, q2, and q3 ​form the basis of the orthogonal matrix Q. These vectors are essential because they provide the foundation for expressing the original data in a new coordinate system.

Here, we see that the Gram Schmidt process is an iterative process that ensures that each successive vector is orthogonal to the previous ones. We also remember that orthogonality means that the dot product of two vectors is zero, indicating that they are perpendicular to each other in the vector space. Let’s confirm the orthogonality of q1 and q2 using their dot product:

# Calculate the dot product of q1 and q2
dot_product_q1_q2 <- sum(q1 * q2)

# Print the dot product to confirm orthogonality
print(dot_product_q1_q2)

[1] 2.43295e-16

Constructing the R matrix

Now that we have our Q matrix, we need to construct the R matrix. The R matrix in QR decomposition contains information about the relationships between the columns of the orthogonal matrix Q and the original dataset. It is an upper triangular matrix, and each element of the upper triangular part of R is obtained by calculating the dot product of the corresponding columns of Q and the original data.

To construct the upper triangular matrix R, we need to calculate the dot products of each column of Q with each column of the original dataset. This will result in a matrix that has the same number of rows as the number of columns in Q, and it will be upper triangular due to our previous process.

matrix_A <- matrix_A %>% as.matrix()

# Calculate and display the R matrix by multiplying Q^T and the subset data
R_matrix <- t(Q_matrix) %*% matrix_A

We see that the output of our R matrix looks a bit different this time. The reason is because the qr() function uses Householder reflections with more numerical stability than the Gram Schmidt-inspired process that we created ourselves.

         column_1      column_2  column_3
[1,] -1.185003e+02 -1.611602e+01 -711.9200
[2,]  5.814446e-16 -1.005857e+01 -496.9319
[3,]  7.633287e-15  1.338669e-15  283.7369

We can verify the reconstruction by multiplying Q and R and seeing that we get back matrix_A. Here, %*% is for matrix multiplication in R.  

Q_matrix %*% R_matrix

   column_1 column_2 column_3
 [1,]     21.0    2.620      110
 [2,]     21.0    2.875      110
 [3,]     22.8    2.320       93
 [4,]     21.4    3.215      110
 [5,]     18.7    3.440      175
 [6,]     18.1    3.460      105
 [7,]     14.3    3.570      245
 [8,]     24.4    3.190       62
 [9,]     22.8    3.150       95
[10,]     19.2    3.440      123
[11,]     17.8    3.440      123
[12,]     16.4    4.070      180
[13,]     17.3    3.730      180
[14,]     15.2    3.780      180
[15,]     10.4    5.250      205
[16,]     10.4    5.424      215
[17,]     14.7    5.345      230
[18,]     32.4    2.200       66
[19,]     30.4    1.615       52
[20,]     33.9    1.835       65
[21,]     21.5    2.465       97
[22,]     15.5    3.520      150
[23,]     15.2    3.435      150
[24,]     13.3    3.840      245
[25,]     19.2    3.845      175
[26,]     27.3    1.935       66
[27,]     26.0    2.140       91
[28,]     30.4    1.513      113
[29,]     15.8    3.170      264
[30,]     19.7    2.770      175
[31,]     15.0    3.570      335
[32,]     21.4    2.780      109