Singular Matrix: Key Concepts and Examples in Data Science

A singular matrix is a square matrix that cannot be inverted, meaning it has no multiplicative inverse. This fundamental concept in linear algebra has an immense impact on data science applications, from machine learning algorithms to numerical stability in computational methods.

In this article, we’ll define what makes a matrix singular and explore its mathematical properties and characteristics. We’ll then examine methods for detecting singular matrices. We will understand their real implications in data science, and we will learn how to handle them effectively.

What Is a Singular Matrix?

A singular matrix is a square matrix whose determinant equals zero, making it non-invertible. 

In mathematical terms, for a square matrix A, if det(A) = 0, then A is singular and has no inverse matrix A⁻¹.

The fundamental characteristic of a singular matrix is that its rows or columns are linearly dependent, meaning at least one row (or column) can be expressed as a linear combination of the other rows (or columns). This dependency creates a “deficiency” in the matrix that prevents it from having a unique inverse.

Another way to understand singular matrices is through their rank. A square matrix is singular if and only if its rank is less than its number of rows (or columns). The rank represents the maximum number of linearly independent rows or columns, so when this falls short of the matrix dimensions, singularity occurs.

This concept is important because many algorithms rely on matrix inversion, from solving linear regression problems to implementing certain machine learning techniques. When a matrix is singular, these operations fail, requiring alternative approaches or preprocessing steps to handle the situation.

Properties and Conditions of Singular Matrices

Understanding the mathematical properties of singular matrices helps identify potential issues before they cause computational problems in data science workflows.

• Zero determinant: The determinant of a singular matrix always equals zero, directly indicating non-invertibility. This zero determinant means the matrix transformation is not bijective, allowing multiple input vectors to map to the same output.
• Linear dependence: Singular matrices contain linearly dependent rows or columns, where at least one row can be expressed as a linear combination of the others. This dependency creates redundant information that leads to computational challenges.
• Rank deficiency: A singular n×n matrix has rank less than n, possessing fewer linearly independent rows or columns than its dimension. This deficiency explains why systems involving singular matrices lack unique solutions.
• Zero eigenvalues: At least one eigenvalue of a singular matrix is exactly zero, corresponding to directions in space that get completely collapsed during transformation. The number of zero eigenvalues equals the matrix’s nullity.
• Non-trivial null space: Singular matrices have non-zero vectors that, when multiplied by the matrix, produce the zero vector. The dimension of this null space indicates how much information is lost during transformation.

Now that we have understood the fundamental properties of a singular matrix, let’s contrast them against non-singular matrices.

Singular vs. Non-Singular Matrix

Non-singular matrices are invertible and support reliable numerical computations, while singular matrices lack inverses and require specialized handling. This fundamental divide determines computational feasibility across data science applications. 

These differences apply to each of the fundamental properties of a singular matrix we saw earlier. The table below summarizes the differences between singular and non-singular matrices:

Examples of Singular Matrices

Examining specific examples helps illustrate how singularity manifests in practice and builds intuition for recognizing these matrices.

Simple 2×2 singular matrix

Consider this basic example where one row is a multiple of another:

Simple 2×2 singular matrix (Image by Author)

Here, the second row is exactly half of the first row, creating linear dependence. The determinant is (2×2) — (4×1) = 0, confirming singularity.

Zero row or column

Any matrix containing a row or column of all zeros is automatically singular:

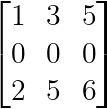
Zero row or column (Image by Author)

The zero row makes it impossible for the matrix to have full rank, regardless of the other entries.

Identical rows or columns

Matrices with identical rows or columns are always singular:

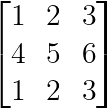
Identical rows or columns (Image by Author)

The first and third rows are identical, creating perfect linear dependence.

Linear combination dependency

A more subtle singularity occurs when one row equals a combination of others:

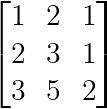
Linear combination dependency (Image by Author)

Here, the third row equals the sum of the first two rows: [3,5,2] = [1,2,1] + [2,3,1].

Each of these examples shown above demonstrates how seemingly different matrices can share the fundamental property of linear dependence that defines singularity.

Why Do Singular Matrices Occur in Data Science?

Singular matrices frequently emerge in data science applications due to the nature of real-world data and common analytical workflows.

Multicollinearity in feature sets

The most common source of singular matrices in data science is multicollinearity, when multiple features in a dataset are perfectly or nearly perfectly correlated. This creates linear dependence among columns in the design matrix, leading to singularity during matrix operations.

Consider a retail dataset where you have features for total_sales, q1_sales, q2_sales, q3_sales, and q4_sales. If the quarterly sales values always sum exactly to the total sales, then:

total_sales = q1_sales + q2_sales + q3_sales + q4_sales

When this relationship holds perfectly across all observations, the resulting design matrix becomes singular. Any linear regression algorithm attempting to invert this matrix will fail because one column can be perfectly predicted from the others.

Similar scenarios occur with derived features like:

• Temperature in Celsius and Fahrenheit
• Age and birth year (given a fixed reference year)
• Ratios where the numerator and denominator are also features
• Dummy variables that sum to a constant (the dummy variable trap)

Insufficient data relative to features

High-dimensional datasets with fewer observations than features naturally produce singular matrices. When you have n samples but p features where p > n, the resulting n×n covariance matrix or gram matrix will have rank at most n, making it singular if you need a p×p invertible matrix.

This “curse of dimensionality” commonly affects:

• Genomics data with thousands of genes but hundreds of samples
• Text analysis with large vocabularies but limited documents
• Image processing with high-resolution features but small training sets
• Financial modeling with many economic indicators, but short time series

Data preprocessing 

Common data preprocessing steps can inadvertently introduce singularity:

• Centering transformations: Centering each feature (subtracting the mean) doesn’t cause singularity on its own, but in the presence of other linear dependencies, it can preserve or emphasize them. In cases where features are already nearly dependent, centering may push them closer to exact dependence under limited precision.
• Scaling and normalization: Certain scaling operations can make subtle linear relationships more pronounced, pushing nearly dependent features into perfect dependence due to floating-point precision limits.
• Feature engineering: Creating polynomial features, interaction terms, or basis expansions can introduce unexpected linear relationships. For example, if you create features x, x^², and 2x^² — x, the third feature (2x^² — x) is perfectly determined by the first two.

Understanding these common sources of singularity allows data scientists to implement preventive measures early in their workflows, such as checking for multicollinearity during exploratory data analysis or using regularization techniques proactively.

Now that we understand why singular matrices occur in data science, let’s explore practical methods for detecting them before they cause computational failures.

How to Detect Singular Matrices

The most straightforward way to detect a singular matrix is by checking its determinant. If the determinant of a square matrix is zero, the matrix is singular and non-invertible. This method is simple, mathematically sound, and widely used in practice.

Let us understand how to perform this check using Python:

import numpy as np

# Example 2x2 matrix
A = np.array([[2, 4],
             [1, 2]])

# Calculate the determinant
det_A = np.linalg.det(A)

print(f"Determinant of A: {det_A}")

# Check if matrix is singular
if np.isclose(det_A, 0):
   print("Matrix A is singular.")
else:
   print("Matrix A is non-singular.")

In the example above, we define a 2×2 matrix A and use np.linalg.det() to compute its determinant. Since floating-point arithmetic can introduce small numerical errors, we use np.isclose() to check if the determinant is effectively zero. If it is, we conclude that the matrix is singular. 

We’ll see the output below confirming the singularity:

Output detecting singular matrix. (Image by Author)

This method is both intuitive and practical, making it a reliable first step when diagnosing issues related to matrix invertibility in data science workflows.

How to Handle Singular Matrices in Practice

When encountering singular matrices in data science workflows, several strategies can resolve the computational challenges while preserving analytical integrity.

Regularization techniques

Adding small values to the diagonal (Ridge regularization) is the most common approach for handling near-singular matrices in regression problems. This technique transforms singular matrices into invertible ones while maintaining numerical stability:

# Ridge regularization approach
lambda_reg = 1e-6
A_regularized = A + lambda_reg * np.eye(A.shape[0])

Pseudoinverse computation

The Moore-Penrose pseudoinverse provides a generalized inverse for singular matrices, offering the “best” solution in a least-squares sense:

# Using pseudoinverse for singular matrices
A_pinv = np.linalg.pinv(A)
x = A_pinv @ b 

Dimensionality reduction

Removing linearly dependent features eliminates the singularity at its source. Principal component analysis or feature selection techniques can identify and remove redundant dimensions:

# PCA-based dimensionality reduction
from sklearn.decomposition import PCA
pca = PCA(n_components=0.95) 
X_reduced = pca.fit_transform(X)

Alternative algorithms

Some algorithms are specifically designed to handle singular matrices. QR decomposition with pivoting can solve linear systems even when the coefficient matrix is singular, providing solutions when they exist and identifying inconsistencies when they don’t.

These strategies ensure that singular matrices don’t derail data science projects while maintaining mathematical rigor and interpretability of results.

Conclusion

This article explored singular matrices, which we learned are square matrices with zero determinants that cannot be inverted due to linear dependencies among rows or columns. We looked at why they commonly appear in data science, from multicollinearity and high-dimensional data to issues introduced during preprocessing. 

In this article, we also reviewed ways to detect and handle singular matrices using basic techniques like determinant checks, regularization, pseudoinverses, and dimensionality reduction. (If you are still interested in looking further on your own, tools like condition number analysis or singular value decomposition can offer even more insight into matrix behavior and numerical stability.)

To deepen your understanding of linear algebra and its critical role in data science applications, enroll in our Linear Algebra for Data Science course, where you’ll master these fundamental concepts and their implementations in real-world scenarios.