Método de los mínimos cuadrados: Cómo encontrar la línea de mejor ajuste

Imagina que intentas predecir los precios de la vivienda basándote en los metros cuadrados. Tienes puntos de datos de ventas recientes, pero no forman un patrón perfecto. Algunas viviendas se venden por más de lo esperado, y otras por menos. ¿Cómo encontrar la mejor línea de tendencia que refleje la relación global entre tamaño y precio sin dejar que las viviendas individuales desvíen tu predicción?

El método de los mínimos cuadrados puede ser la solución que necesitas. En este artículo, exploraremos los conceptos básicos del método de los mínimos cuadrados, sus variaciones y aplicaciones. Al final, tendrás una sólida comprensión de cómo utilizar este método y aplicarlo a problemas reales.

¿Qué es el método de los mínimos cuadrados?

El método de los mínimos cuadrados es una técnica estadística utilizada para determinar la línea o curva que mejor se ajusta a un conjunto de puntos de datos. Funciona minimizando las diferencias al cuadrado entre los valores observados y los predichos en un conjunto de datos. La diferencia entre los puntos de datos reales y los valores predichos por el modelo se denominan residuos. El objetivo es encontrar un modelo que minimice la suma de estos residuos al cuadrado, dando lugar a las predicciones más exactas posibles.

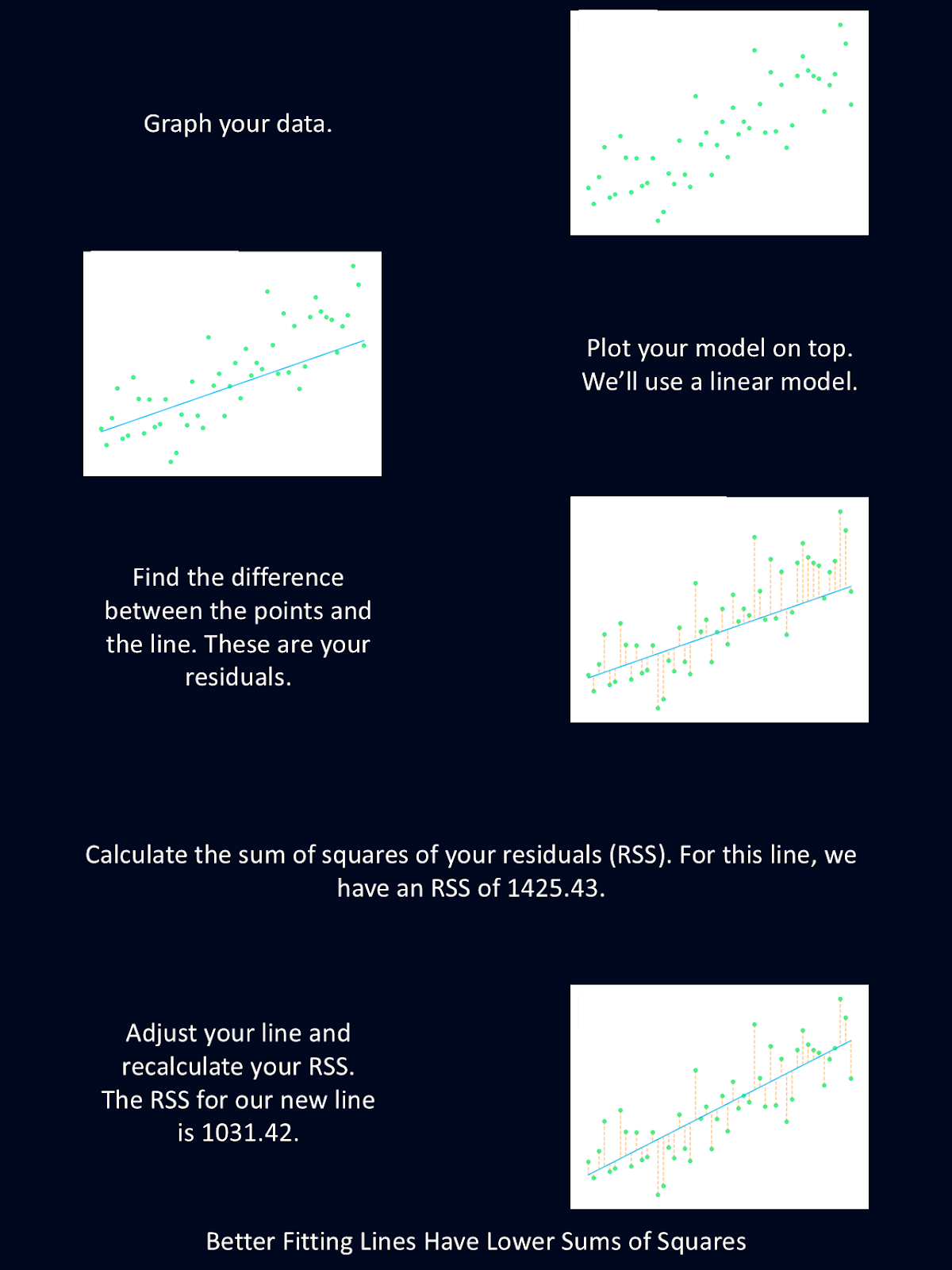
El diagrama anterior explica brevemente los pasos del método de los mínimos cuadrados.

Este método fue derivado por Carl Friedrich Gauss, de 18 años, en 1895 (puede que reconozcas su nombre por la distribución gaussiana). Adrien-Marie Legendre formalizó posteriormente la técnica en 1805 y fue el primero en escribir un artículo utilizando el método de los mínimos cuadrados para reconstruir la órbita de un asteroide. 

Cómo funciona el método de los mínimos cuadrados

El método de los mínimos cuadrados encuentra la línea que mejor se ajusta a un conjunto de puntos minimizando la suma de las diferencias al cuadrado entre los valores observados y los valores predichos. Se utiliza para encontrar los parámetros del modelo con el mayor ajuste posible.

Probemos esto con un conjunto de datos extremadamente pequeño: sólo 10 puntos. En primer lugar, tenemos que elegir un modelo que se ajuste a nuestros datos. Para este sencillo ejemplo, elegiremos una regresión lineal simple, lo que significa que estamos realizando una regresión en la que sólo tenemos exactamente una variable independiente y una dependiente.

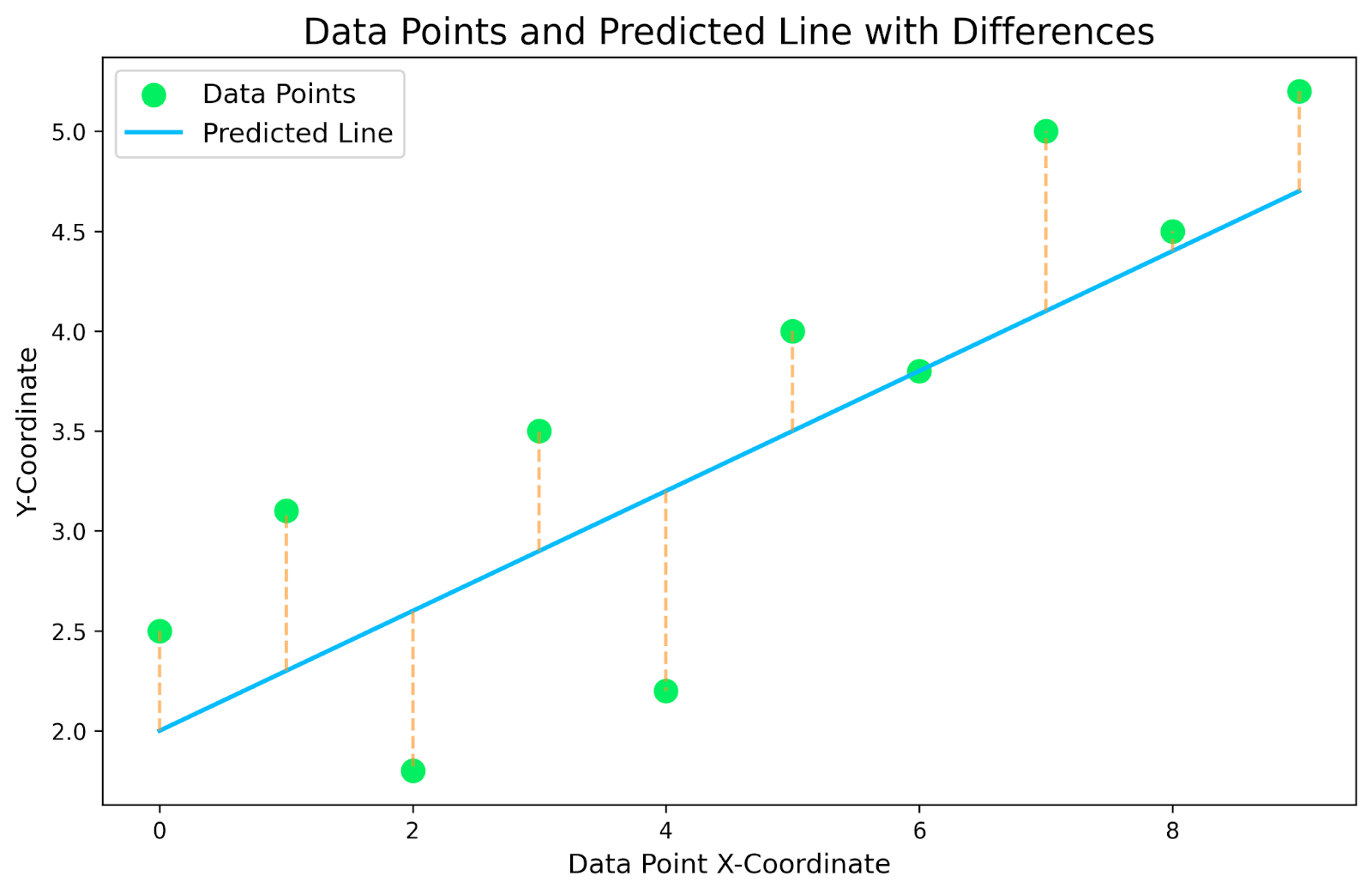
El gráfico anterior es un gráfico de nuestro pequeño conjunto de datos, con una regresión lineal gráficando encima. Las líneas de puntos amarillas que conectan los puntos de datos con la línea prevista son los residuos. El objetivo es encontrar el modelo de regresión lineal que minimice estas líneas residuales de puntos amarillos.

Para cada punto de datos de nuestro conjunto de datos, tenemos que encontrar la diferencia de coordenadas y entre el punto de datos y la recta. Éstos serán nuestros residuos. A continuación, elevamos al cuadrado cada residuo para eliminar los números negativos de y tomamos la suma total. Esto nos dará una idea de lo bien que se ajusta nuestra recta a nuestros datos. Consulta la tabla siguiente para ver el desglose de nuestro gráfico específico.

Ahora que tenemos una idea de lo bien que se ajusta esta recta a nuestros datos, podemos modificar los parámetros de la recta, ya sea su pendiente o su intercepto, y volver a realizar nuestros cálculos. La línea que tiene la menor suma de residuos al cuadrado es la que mejor se ajusta a nuestros datos. Por lo tanto, esa línea nos dará las mejores predicciones.

Utilizar el método de los mínimos cuadrados para encontrar la mejor línea

En el ejemplo anterior, no hemos encontrado la línea que mejor se ajusta. En lugar de eso, nos limitamos a calcular lo bien que se ajustaba esa recta a los datos. Ahora podríamos iterar por un montón de líneas potenciales y realizar el mismo cálculo para encontrar las que mejor se ajusten. O podríamos utilizar un poco de álgebra para encontrar la mejor línea más rápidamente. Intentémoslo.

Empezaremos con la ecuación de la regresión lineal: y=mx+b, donde b es el intercepto y m es la pendiente. Ahora inventemos algunos datos.

En primer lugar, tenemos que calcular la media de los valores X e Y. Éstos serán nuestros valores previstos:

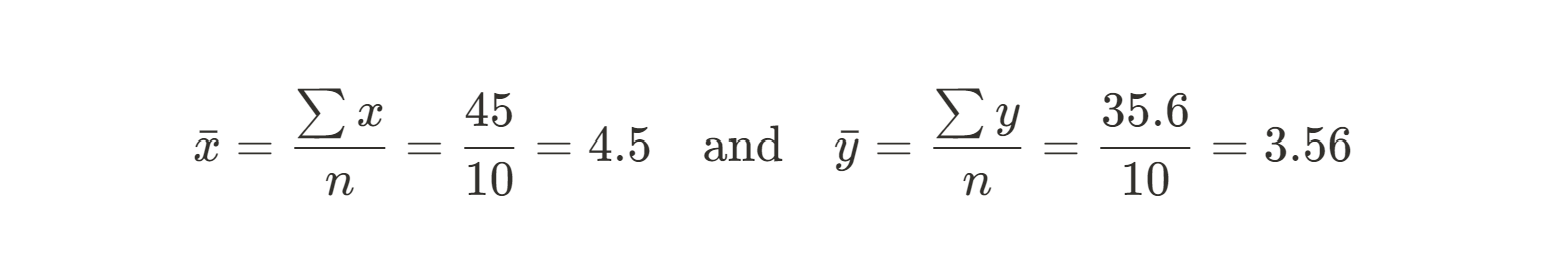
A continuación, podemos utilizar la suma de los cuadrados de nuestros residuos entre cada punto de datos y nuestro valor predicho (la media) para hallar la pendiente. Ésta es la ecuación que utilizaremos:

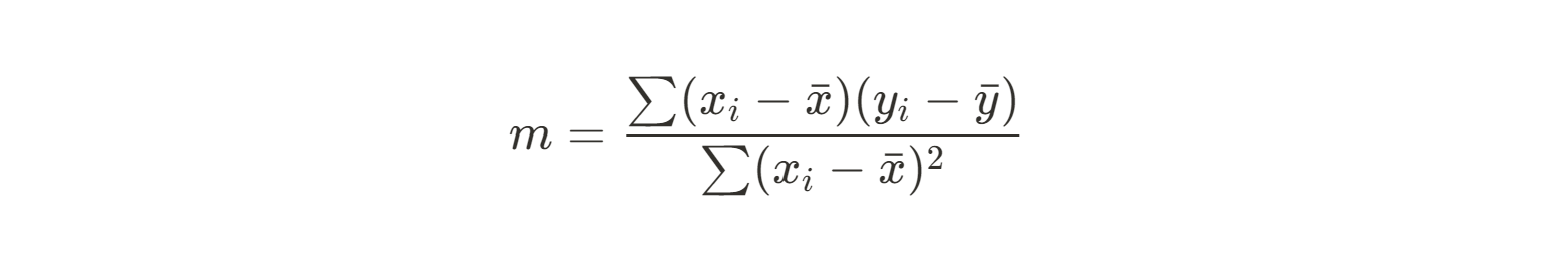
Como se trata de una ecuación bastante difícil de hacer a mano, calcularemos el numeradory el denominador por separado. Empecemos por el numerador:

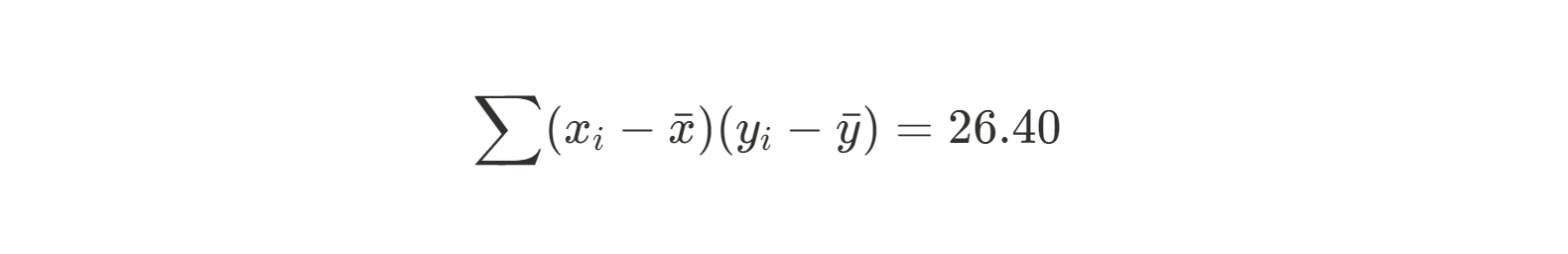
Ahora hagamos lo mismo con el denominador:

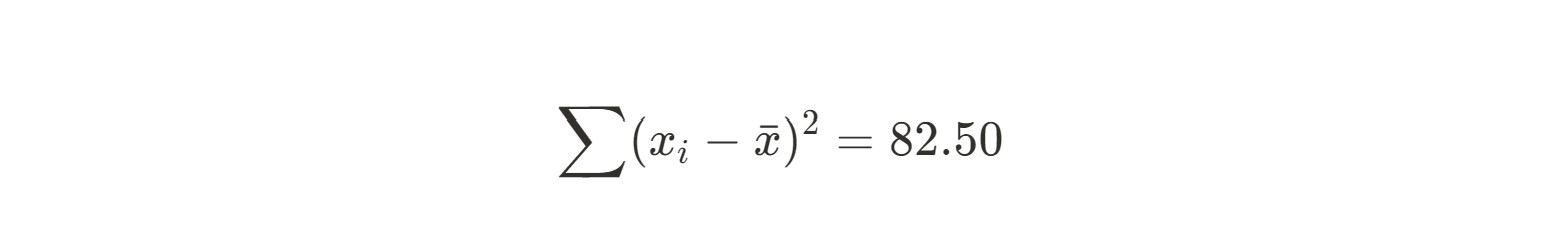
Ahora podemos calcular la pendiente de nuestra recta de mejor ajuste.

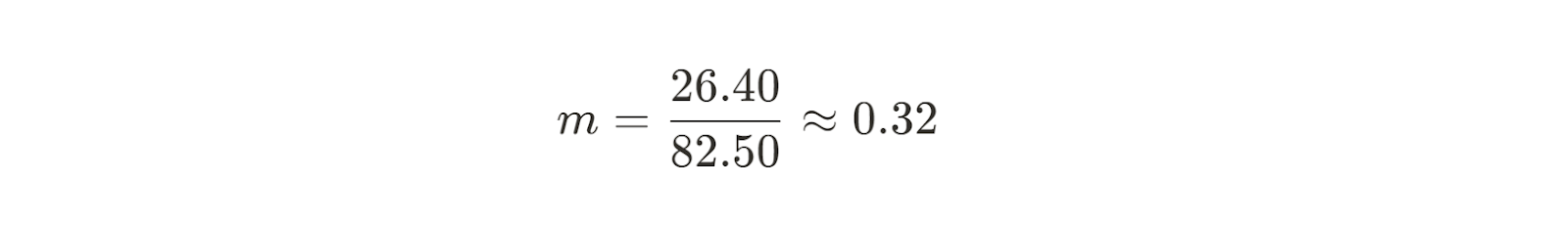
Ahora ya sabemos cuál es la pendiente de la recta que mejor se ajusta a nuestros datos. A continuación, tenemos que encontrar el intercepto y. La fórmula para el intercepto b es fácil de encontrar con un poco de reordenación algebraica:

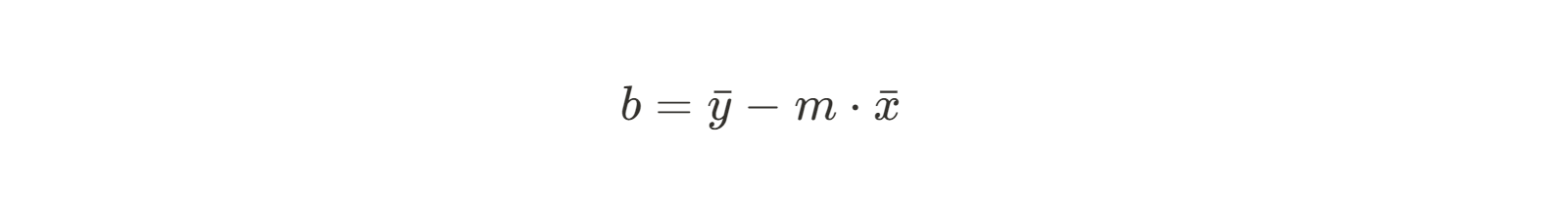
Como ya conocemos la pendiente, podemos insertar simplemente nuestras medias x e y y resolver para b.

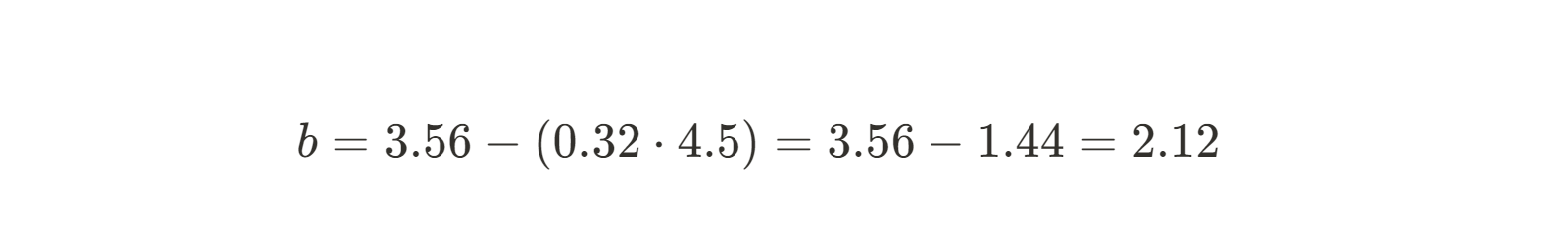
Ahora que tenemos tanto m como b, podemos escribir la ecuación de la recta que mejor se ajusta:

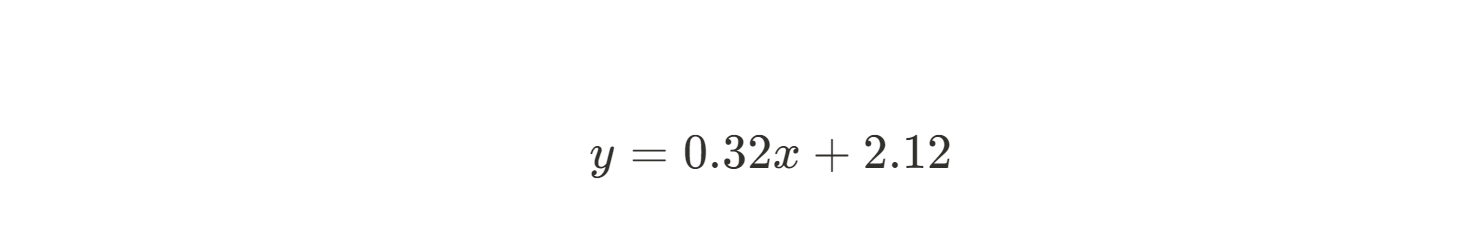
El método de los mínimos cuadrados nos permitió obtener rápida y fácilmente la mejor recta de regresión lineal, ¡incluso a mano! Evidentemente, cuantos más datos tengas, más difícil será hacerlo a mano. Afortunadamente, dado que las matemáticas son bastante sencillas, es muy fácil implementar este método en Python o R. Para obtener explicaciones detalladas sobre cómo hacerlo, consulta Essentials of Linear Regression in Python (Aspectos básicos de la regresión lineal en Python ) y How to Do Linear Regression in R (Cómo hacer regresión lineal en R).

Fundamentos matemáticos del método de los mínimos cuadrados

Antes hemos utilizado un ejemplo de regresión lineal simple y hemos hallado la pendiente y el intercepto mediante bonitas ecuaciones de forma cerrada, y hemos modelado la variable dependiente en función de la variable independiente: y=mx+b.

Sin embargo, las ecuaciones que he mostrado antes sólo funcionan cuando tienes una variable independiente. Otra forma de hallar los coeficientes de una regresión es utilizar lo que se conoce como ecuación normal, que proporciona una solución matricial al problema de los mínimos cuadrados. La ecuación normal se refiere a la ecuación matricial que resulta de minimizar la suma de los residuos al cuadrado mediante el método de los mínimos cuadrados. Geométricamente, y utilizando el lenguaje del álgebra lineal, la solución de mínimos cuadrados puede visualizarse como la proyección ortogonal del vector de datos observados sobre el espacio de columnas de la matriz del modelo. En pocas palabras, esto sólo significa que los errores se minimizan de forma que se garantice que los valores predichos se aproximan lo más posible a los datos observados, dadas las restricciones del modelo.

En los casos en que la matriz no es invertible (lo que significa que el sistema de ecuaciones no tiene una solución única), la pseudoinversa de Moore-Penrose proporciona una forma de calcular una solución por mínimos cuadrados. Esto nos da flexibilidad para manejar situaciones en las que el sistema está infradeterminado (lo que significa que hay más incógnitas que ecuaciones) o sobredeterminado (lo que significa que hay más ecuaciones que incógnitas).

Si necesitas un repaso del álgebra matricial, te recomiendo el curso Álgebra Lineal para la Ciencia de Datos en R.

Tipos de métodos de mínimos cuadrados

Hasta ahora, sólo hemos hablado de utilizar el método de los mínimos cuadrados con un estimador de mínimos cuadrados ordinarios. Sin embargo, es una herramienta versátil que puede adaptarse a muchos escenarios dependiendo de la naturaleza del problema que estés abordando. Exploremos algunos tipos de métodos de mínimos cuadrados, lo que los hace únicos y sus usos prácticos.

Mínimos cuadrados lineales

Llegados a este punto, deberías estar bastante familiarizado con los mínimos cuadrados lineales (tambiéndenominados mínimos cuadrados ordinarios). Se utiliza con modelos que tienen coeficientes lineales, como en laregresión lineal simple o múltiple . El objetivo es encontrar la línea (o hiperplano, en el caso de regresiones lineales múltiples) que minimice la suma de los residuos al cuadrado.

Este tipo de mínimos cuadrados supone que los residuos tienen una varianza constante y que no hay valores atípicos significativos en los datos. Se puede aplicar a la mayoría de las cosas que tienen una relación lineal. Por ejemplo, podrías utilizarlo para las relaciones entre la duración de la gestación y el peso al nacer o entre el gasto en publicidad y los ingresos por ventas. Éste es el tipo de mínimos cuadrados que utilizo más a menudo y del que oigo hablar a otros con más frecuencia.

Mínimos cuadrados ponderados

Los mínimos cuadrados ponderados son una ampliación de este método que funciona cuando la varianza de los residuos no es constante. Al asignar pesos a cada punto de datos, los mínimos cuadrados ponderados dan más importancia a las observaciones con menor varianza. La ecuación para ello es similar a la suma de cuadrados anterior, pero con un peso (w_i) aplicado a cada residuo:

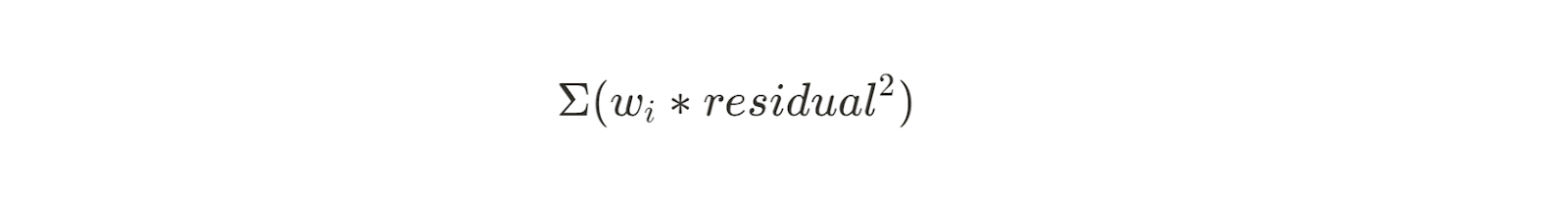
Este método es útil para conjuntos de datos en los que el error de medición varía entre las observaciones, por ejemplo en la calibración de sensores. Las ponderaciones suelen ser la inversa de la varianza de cada observación.

Mínimos cuadrados robustos

Los mínimos cuadrados robustos están diseñados para manejar conjuntos de datos con valores atípicos que pueden influir desproporcionadamente en los resultados de los mínimos cuadrados ordinarios. Utiliza técnicas iterativas de reponderación para reducir el impacto de los valores atípicos.

En los mínimos cuadrados robustos, puedes utilizar métodos como los mínimos residuos absolutos (LAR) o las ponderaciones bicuadradas para ajustar iterativamente las ponderaciones y restar importancia a la influencia de los valores atípicos.

Un ejemplo de cuando podrías utilizar esto es con la modelización financiera, donde quieres tener en cuenta las caídas extremas del mercado. Si tienes un conjunto de datos en el que no quieres eliminar los valores atípicos, pero aún así quieres tenerlos en cuenta, los mínimos cuadrados robustos pueden ser el camino a seguir.

Mínimos cuadrados no lineales

Los mínimos cuadrados no sólo se utilizan con regresiones lineales. Los mínimos cuadrados no lineales se utilizan cuando el modelo que estás aplicando no es lineal en sus coeficientes. Esto es más complicado que los mínimos cuadrados lineales , y puede requerir técnicas de optimización iterativas (como Gauss-Newton o Levenberg-Marquardt) para encontrar el mejor ajuste.

Es importante tener cuidado con los mínimos cuadrados no lineales. El cálculo puede ser sensible a las estimaciones iniciales de los parámetros, así como a problemas de convergencia. Algunos ejemplos de su uso son la modelización del crecimiento exponencial de los virus en un organismo durante una infección o la modelización de las velocidades de reacción química en el laboratorio.

Mínimos cuadrados totales

Hasta ahora, hemos hablado sobre todo de casos en los que sólo la variable dependiente tiene errores. Y hemos minimizado las distancias verticales entre nuestro modelo y nuestros datos. Pero, ¿y si también tienes errores en tus mediciones independientes?

Los mínimos cuadrados totales son útiles cuando tanto la variable independiente como la dependiente tienen errores de medición. Este método tiene en cuenta los errores en todas las variables. Esto puede ser especialmente útil en campos como la astronomía y la geodesia (el campo que mide la forma de la Tierra y el campo gravitatorio), donde los errores de medición están presentes en todas las dimensiones debido al alto nivel de precisión necesario. Los mínimos cuadrados totales suelen utilizarse junto con la descomposición en valores singulares.

Mínimos cuadrados generalizados

Los mínimos cuadrados generalizados son una ampliación del método de los mínimos cuadrados que aborda los retos que plantean los residuos correlacionados. Con los mínimos cuadrados generalizados, transformamos los datos a una forma en la que se puedan aplicar los mínimos cuadrados ordinarios. Esta transformación consiste en utilizar la matriz de covarianza de los residuos para tener en cuenta su estructura de correlación, lo que permite unas estimaciones más precisas de los parámetros.

Esto puede ser especialmente útil en situaciones como los análisis de series temporales, en los que los residuos pueden presentar autocorrelación. 

Aplicaciones del método de los mínimos cuadrados

El método de los mínimos cuadrados es una técnica estadística muy utilizada, con aplicaciones en numerosos campos.

En estadística y ciencia de datos, los mínimos cuadrados se utilizan para construir modelos de regresión lineal y no lineal para hacer predicciones basadas en entradas conocidas. También es útil para analizar tendencias, sobre todo en datos de series temporales.

En finanzas, los mínimos cuadrados se utilizan en el análisis del rendimiento de las acciones, ayudando a determinar la relación entre el rendimiento de una acción y los índices del mercado. Por ejemplo, puede utilizarse para calcular la sensibilidad de una acción a los movimientos del mercado. También ayuda a modelar el riesgo ajustando modelos a datos financieros históricos para estimar el riesgo y el rendimiento.

Los ingenieros utilizan los mínimos cuadrados en la calibración de los sensores para ajustar los modelos a los datos observados y minimizar los errores de medición. También se aplica en el procesamiento de señales para filtrar y reducir el ruido, lo que permite una interpretación más clara de los datos.

Por supuesto, los mínimos cuadrados tuvieron su origen en la astronomía; su primer uso fue por Carl Friedrich Gauss para predecir la órbita del asteroide Ceres. También se utiliza en geodesia para modelar la forma de la Tierra a partir de datos de observación, lo que es esencial para realizar mediciones geográficas precisas.

Si te has adentrado en el machine learning, reconocerás el método de los mínimos cuadrados como un método para minimizar la función de pérdida durante el entrenamiento de modelos de regresión lineal. Puede que también lo hayas utilizado durante la selección de características para identificar las variables más importantes que contribuyen al modelo.

También desempeña un papel en muchas otras ciencias duras, como la física y la química. Puede utilizarse para ajustar curvas a datos experimentales, como velocidades de reacción o medidas físicas, y ayudar a minimizar los errores en las configuraciones experimentales.

El método de los mínimos cuadrados es una herramienta estadística versátil. Personalmente, he utilizado este método para calibrar sensores de presión, hacer predicciones basadas en mis datos experimentales y durante el entrenamiento de machine learning. La capacidad de modelar relaciones de forma fiable y minimizar los errores es una característica que ofrece valor a muchas disciplinas diferentes.

Supuestos y diagnóstico

El método de los mínimos cuadrados hace algunas suposiciones clave sobre tus datos y el modelo utilizado. Es importante comprender estos supuestos, porque violarlos puede conducir a resultados sesgados o poco fiables. Por tanto, vamos a discutir estos supuestos, así como la forma de diagnosticar y abordar los posibles problemas.

Un supuesto es la independencia de los errores, lo que significa que los residuos no deben estar correlacionados. Si los errores están correlacionados entre sí, sobre todo en datos secuenciales o espaciales, las estimaciones pueden distorsionarse. La prueba de Durbin-Watson puede detectar autocorrelación en los residuos, especialmente en conjuntos de datos dependientes del tiempo. Si encuentras una correlación, puedes utilizar los mínimos cuadrados generalizados para tenerla en cuenta.

Otro supuesto es que la varianza de los residuos permanece constante en todos los niveles de la variable independiente. Si los residuos muestran una dispersión en forma de embudo cuando se grafican frente a los valores ajustados, es probable que se infrinja este supuesto. Para resolver este problema, puedes utilizar los mínimos cuadrados ponderados para asignar ponderaciones adecuadas a tus observaciones. Alternativamente, puedes utilizar transformaciones como ajustes logarítmicos o de raíz cuadrada para estabilizar la varianza desigual y solucionar cualquier problema de heteroscedasticidad.

Como en toda modelización, es importante que la estructura refleje la relación subyacente entre las variables. Si no es así, no importa lo optimizado que esté tu ajuste; los resultados seguirán siendo engañosos. Los gráficos de residuos y las métricas de bondad de ajuste, como ^R², pueden ayudarte a determinar si el modelo elegido capta los patrones de los datos. 

El método estándar de mínimos cuadrados supone que las variables independientes se miden sin error. Por eso es importante conocer la precisión de tu medida independiente. Deberías hacerte una idea de la precisión de esta medida observando los métodos de recogida. Si existen errores de medición en tu predictor, asegúrate de utilizar el método de mínimos cuadrados totales para mitigar las imprecisiones en tu modelización.

Por último, la distribución de los errores residuales desempeña un papel importante, sobre todo en la comprobación de hipótesis y la estimación de intervalos de confianza. Los mínimos cuadrados suponen que los errores siguen una distribución normal (gaussiana), y las desviaciones de la normalidad pueden afectar a la inferencia. Los histogramas y los gráficos Q-Q ayudan a evaluar si los residuos se ajustan a las distribuciones esperadas. Si tienes desviaciones significativas de la normalidad, las técnicas de regresión robusta o los métodos de bootstrapping pueden proporcionar estimaciones más fiables y menos sensibles a los valores atípicos.

Ventajas y desventajas de los mínimos cuadrados

El método de los mínimos cuadrados es una herramienta muy utilizada en el análisis de datos. Pero eso no significa que deba utilizarse para todos los conjuntos de datos.

El método de los mínimos cuadrados ofrece varias ventajas. Es bastante fácil de calcular, sobre todo para los modelos lineales. Es fácilmente interpretable tanto por el público técnico como por el no técnico. Además, hay diferentes estilos, como regresión ponderada, robusta y no lineal, lo que la hace muy versátil. Y lo que es más importante, tiene una sólida base teórica proporcionada por el teorema de Gauss-Markov. Todo esto hace que los mínimos cuadrados sean ampliamente aplicables y se utilicen en campos que van desde la economía a la ingeniería.

Sin embargo, el método es sensible a los valores atípicos, que pueden afectar desproporcionadamente a los resultados del modelo. También supone que no hay errores en los predictores, lo que puede no ser cierto en los datos del mundo real. Además, los mínimos cuadrados pueden verse limitados por la multicolinealidad. Lo que significa que los predictores muy correlacionados pueden dar lugar a coeficientes inestables y, por tanto, a estimaciones poco fiables. También requiere una varianza constante de los residuos, condición que no siempre se cumple.

Es importante que examines detenidamente tu conjunto de datos y tu objetivo antes de decidir que el método de los mínimos cuadrados es la mejor herramienta para tu circunstancia.

Conclusión

El método de los mínimos cuadrados es una herramienta fundamental para cualquier analista de datos. Al encontrar el mejor ajuste para nuestros datos, podemos hacer predicciones más precisas y encontrar tendencias más perspicaces.

Para leer más sobre la medición de rectas en el espacio euclídeo, te recomiendo nuestro Comprender la distancia euclídea: De la teoría a la práctica tutorial. Además, asegúrate de matricularte en nuestros cursos de regresión para convertirte realmente en un experto. 

• Introducción a la regresión con modelos estadísticos en Python
• Introducción a la regresión en R