What is Double Descent in Machine Learning?

The traditional rule of statistical modeling states that if the model gets more complicated, the training error goes down, but the test error goes up because of overfitting. Keep it simple, and you might underfit. That’s the classic bias-variance tradeoff we’ve been taught for decades.

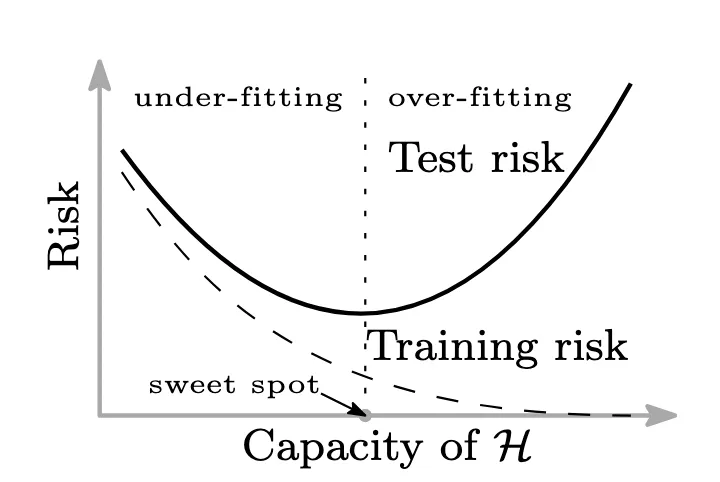
The classical bias-variance trade-off. Source: Adapted from Figure 1(a) in Belkin et al., 2019

But modern machine learning, especially deep learning, challenges this elegant idea. If you’ve worked in deep learning in the last few years, you may have noticed something strange: models with millions of parameters still generalize surprisingly well.

That’s not supposed to happen as per conventional wisdom. Or is it?

Enter double descent: a strange but fascinating phenomenon where increasing model complexity again improves performance after a sudden rise in test error.

This isn’t just a quirky academic concept, it has actually helped me make sense of counterintuitive trends I’ve observed in real-world machine learning projects. As someone who's spent years leading forecasting, churn prediction, and NLP initiatives for large-scale systems, I’ve seen firsthand how this phenomenon challenges traditional wisdom and reshapes how we approach model complexity.

In this article, we'll talk about what double descent is, its phases, when and why it happens, and most importantly, what to do about it.

A Brief History of Double Descent

Double descent may seem like a novel idea, but most people are unaware that it’s an old concept, which was brought back into sharper focus by deep learning. 

Early observations: The non-monotonic error mystery

The idea that increasing model complexity could lead to better generalization after overfitting isn't entirely a new idea. In fact, classical statistics hinted at this strange behaviour decades ago. For example, when fitting high-degree polynomials to data in linear regression, you can see the pattern of overfitting followed by better generalization. But people often said that these patterns were just artifacts of overfitting or numerical instability, not real behaviour.

Modern rediscovery: Deep learning forced a rethink

The turning point came with the success of deep neural networks, where models often had millions or even billions of parameters, which is a lot more than the amount of training examples. 

Classical wisdom suggests that complex models should overfit training data significantly. However, surprisingly, this isn't the case. In fact, these models often generalize better than smaller ones. 

This unexpected finding led researchers like Belkin et al. (2019) to explore older theories. Their fascinating discovery revealed that once a model becomes complex enough to perfectly fit the training data, test error actually begins to improve again as the model increases in size. Deep learning didn't just uncover this phenomenon known as 'double descent'—it transformed it into a fundamental concept in our understanding of generalization today.

What Is Double Descent? Definition, Intuition, and the Risk Curve

Double descent refers to the observation that the test error curve isn’t always U-shaped with respect to model complexity. After the initial descent (as bias decreases), the test error increases (due to overfitting), but then, unexpectedly it starts decreasing again. This forms the “double descent” shape.

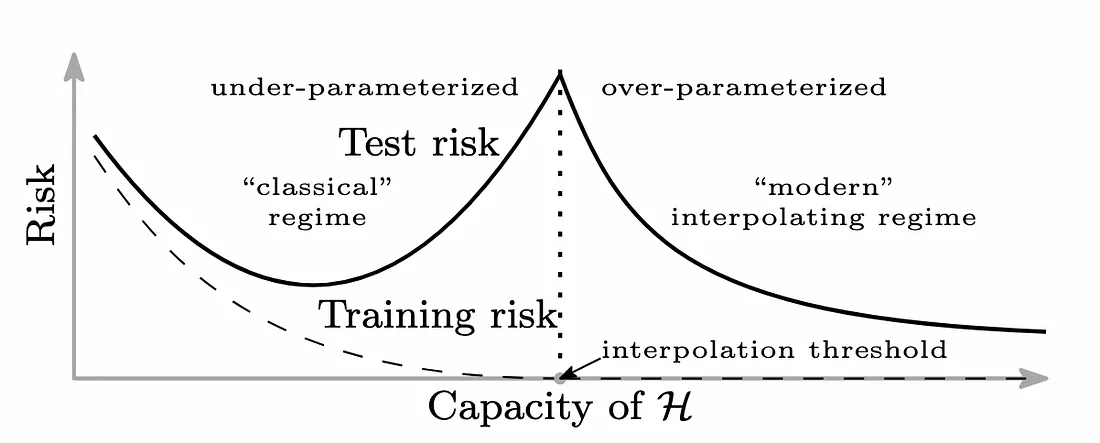
The double descent risk curve. Source: Adapted from Figure 1(b) in Belkin et al., 2019

In my own practice, especially while deploying deep learning-based text classification systems and performing time series forecasting for supply chain corporations, I observed this second dip in test error. It wasn’t theoretical; it was visible in our validation curves.

It helps explain why large models such as ResNets, and in general, massively overparameterized architectures, can still generalize well. While scaling laws for models like GPT suggest smoother improvements rather than a visible double descent curve, the underlying principle—that bigger isn’t always worse—remains relevant.

Fundamental principles and phases of Double Descent

There are three main stages of double descent discussed below. 

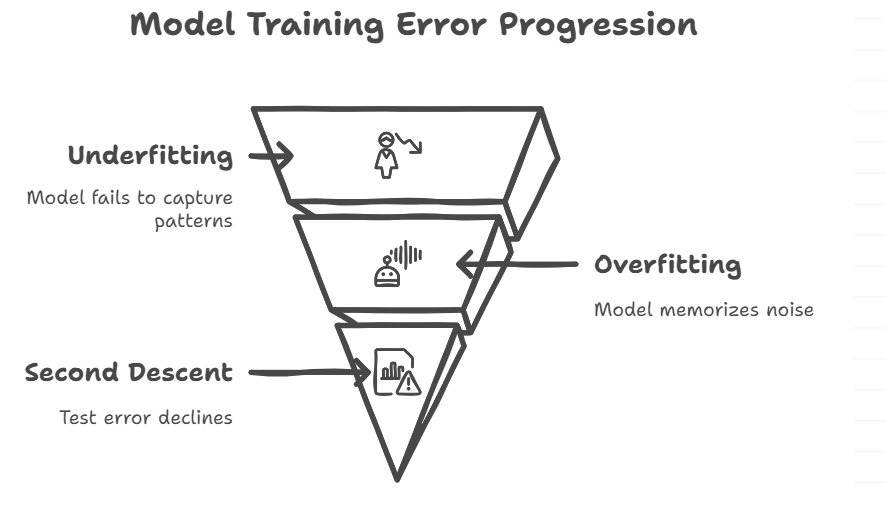
Phases of Double Descent. Source of Image: Napkin AI

Underfitting Phase

• Characteristics: Models are too weak to capture patterns (e.g., linear regression on image data).
• Behavior: Adding parameters reduces bias, but only up to a point.

From my experience: Start simple, but don’t fear complexity.

Overfitting Phase (The Danger Zone)

• Characteristics: Models memorize noise which leads to sharp spikes in the test error. 
• The twist: This is where most stop training—but it’s not the endpoint.

Practical tip: If your validation loss spikes mid-training, pause—but don’t terminate.

Second Descent Phase

• Characteristics: Test error declines despite perfect training fit.
• Mechanism: Overparameterization lets optimization (like SGD) find "simpler" solutions. 

Key insight: Big models aren’t inherently chaotic—they’re implicitly regularized. 

One leading explanation is that optimizers like SGD inherently prefer flatter minima, those with lower curvature, that tend to generalize better. Even in massively overparameterized models, these flatter regions become easier to find as the optimization landscape changes.

Dimensional Manifestations of Double Descent

One of the most fascinating aspects of double descent is that it doesn’t just show up when scaling model size. It also appears across epochs and training data size—something I’ve noticed while running experiments with varying training lengths and data splits.

Model-wise double descent

This is the most commonly studied form. When we add more parameters, we go from underfitting to interpolation and then to overparameterization. Adding more parameters beyond the interpolation threshold may actually help, according to double descent. This idea, which goes against common sense, has been seen in deep neural networks and polynomial regression.

Model-wise double descent allows us not to be afraid of large models as long as they are trained properly. It's also a reminder that cutting back on models too soon could mean sacrificing performance for no reason.

Epoch-wise double descent

Another type of descent happens when you train for a longer time. At first, more training makes performance better. Then the test error goes up (overfitting). But it could fall again with continued training. This happens a lot when you use methods like learning rate decay or weight averaging, which facilitates search to find flatter minima later in training. 

So, in some cases, continued training beyond the overfitting point can lead to improved generalization. However, this is highly context-dependent and should be guided by careful validation—blindly extending training can worsen overfitting in many practical cases.

Sample-wise double descent

The most surprising aspect is that double descent can also happen with the amount of training data. At first, adding more data makes things work better. But there are times, especially when there is a lot of noise in data, when the model might have trouble, which makes the test error go up. Eventually, generalization gets better again as more useful data is added. This kind of double descent shows us that more data isn't always better right away, but it usually pays off in the end.

Theoretical Mechanisms and Mathematical Foundations

To understand why double descent happens, we need to dig into concepts such as optimization dynamics, geometry, and learning theory.

Spectral analysis

We can look at the curvature of the loss surface using singular value decomposition (SVD). Around the interpolation threshold, models are very sensitive to input directions with small singular values, which are directions with low signal-to-noise ratios. This spikes the model test error, which are basically the "weak directions" where noise can have a big effect on overfitting.

Implicit regularization

One of the most widely accepted ideas is that stochastic gradient descent (SGD) implicitly makes the solution more stable. SGD prefers weight configurations with low norm or low curvature, over multiple configurations, to minimize loss. These are simpler solutions in a high-dimensional space. These flat minima are less affected by changes and are often linked to better generalization, especially in the second descent.

Role of noise

Noise is a tricky thing. At the interpolation threshold, even a little bit of label noise can make the model fit it, which can lead to big gaps in generalization. But if the optimizer does a good job, and you have a significant number of parameters, the model will be able to separate the signal from noise. This backs up the idea that overparameterization isn't a problem if optimization is done correctly.

Alternative theories

The Lottery Ticket Hypothesis says that big networks have small, trainable subnetworks that work well; and the larger models make it easier to find them. The sharp vs. flat minima theory says that the shape of the loss surface has a bigger effect on generalization than the size of the model. 

Together, these perspectives create a richer understanding of why double descent arises.

Empirical Examples and Evidence

Benchmark experiments

Some of the earliest studies that showed double descent were done by Belkin et al. (2019). They tried out polynomial regression and neural networks models; and found that test error doesn't just go up and flatten; it can go down again as well. These benchmarks made a phenomenon that many people in the deep learning community had noticed anecdotally.

Deep learning case studies

When the depth of the layers in ResNets on CIFAR-10 and ImageNet increases, the double descent performance is exhibited. Even with fixed data, transformers like GPT-2/3/4 get better at generalizing as the model size grows. When filters, layers, or units are made bigger, CNNs trained on vision datasets often follow the double descent curve.

Practical Implications for Model Development

Learning about double descent isn't just an academic exercise, it can help organizations make better choices in real-life ML projects.

Model scaling

This concept tells us that bigger isn’t always worse. In fact, increasing the model's capacity beyond the point of overfitting might help it generalize better, especially if you optimize and regularize it correctly. Having said that, we should still weigh the benefits of better performance against the costs of computing and the effects on the environment.

Training protocols

For instance, using dropout after the interpolation threshold can stabilize learning in the second descent phase. You could try longer training schedules, cyclical learning rates, or even delay regularization until after the interpolation peak. This can make learning more stable during the second descent phase.

Data management

Double descent also helps with planning how to collect data. When you hit that ugly interpolation peak (where error spikes despite perfect training accuracy), the knee-jerk reaction is to dump more raw data into the model. Don't. Because sample-wise double descent means more data can initially amplify noise sensitivity before helping.

Instead consider using methods like active learning, data augmentation, and stratified sampling instead of giving the model more data. These can help the model get through the interpolation peak more easily. Monitor data impact with DataCamp's Data Quality Dimensions Cheat Sheet.

Mitigation and diagnostics

To help cut down on overfitting near the interpolation threshold, think about tools like dropout, batch norm, and weight decay. These can help you figure out if you're in the danger zone or getting close to the second descent sweet spot.  I personally have used these techniques in several modelling projects, especially when working on imbalanced or noisy datasets.

Unresolved Questions and Future Research Directions

Despite the growing body of work, double descent raises more questions than it answers. Even though there is more research being done on double descent, there are still some questions that need to be answered along with the direction this exciting field is taking. 

Theoretical gaps

Is it possible to mathematically or statistically predict when exactly double descent will occur? What features of the dataset, the type of architecture, or the choice of the optimizer will determine the shape of the test error curve? These are questions where research can do more work in the future.

Architecture and optimization

Could we design neural networks or training schedules in a manner that makes better use of the second descent? Should we look at overparameterization as a strategic design layer? This is a good start on neural tangent kernels, pretraining dynamics, and architecture search.

Philosophical shifts

Double descent makes us think again about the foundations of learning. It suggests that complexity and generalization don't always go against each other, and that overfitting might not be the worst thing that could happen. That's a big change in the way many classical practitioners think, and it shows that our theories about learning are still evolving.

Conclusion

Double descent is more than just a new twist in machine learning; it is a new way on how we think about generalization. Instead of avoiding or abandoning complex models, we might need to use them strategically. This means having faith in optimization, knowing your data, and being open to trying new things that aren't usually done.

Don't be quick to panic the next time your model starts to overfit. You might be about to meet the second descent. 

Now that you have an understanding of double descent, you can also check out some of the resources and links given below to build upon this learning. 

• Gradient Descent in Machine Learning: A Deep Dive 
• RNA-Seq with Bioconductor in R
• Dimensionality Reduction in R