Qu'est-ce que l'ajustement insuffisant ? Comment détecter et surmonter les biais importants dans les modèles de ML

Lorsque nous construisons des modèles pour prédire des résultats ou découvrir des schémas, nous sommes confrontés à différents défis. L'un des obstacles les plus fréquents est la création d'un modèle qui capture avec précision les tendances sous-jacentes de vos données. Parfois, les modèles sont trop simples et ne parviennent pas à assimiler les complexités, ce qui se traduit par des performances médiocres. Ce phénomène est connu sous le nom d'Underfitting.

Un modèle sous-adapté n'est pas seulement peu performant sur les données sur lesquelles il a été formé, mais il ne parvient pas non plus à se généraliser à de nouvelles données inédites. Cela signifie que vos prédictions pourraient ne pas être fiables dans des scénarios réels. L'identification et la résolution des problèmes d'ajustement insuffisant constituent une étape importante dans la construction de modèles d'apprentissage automatique robustes et efficaces. 

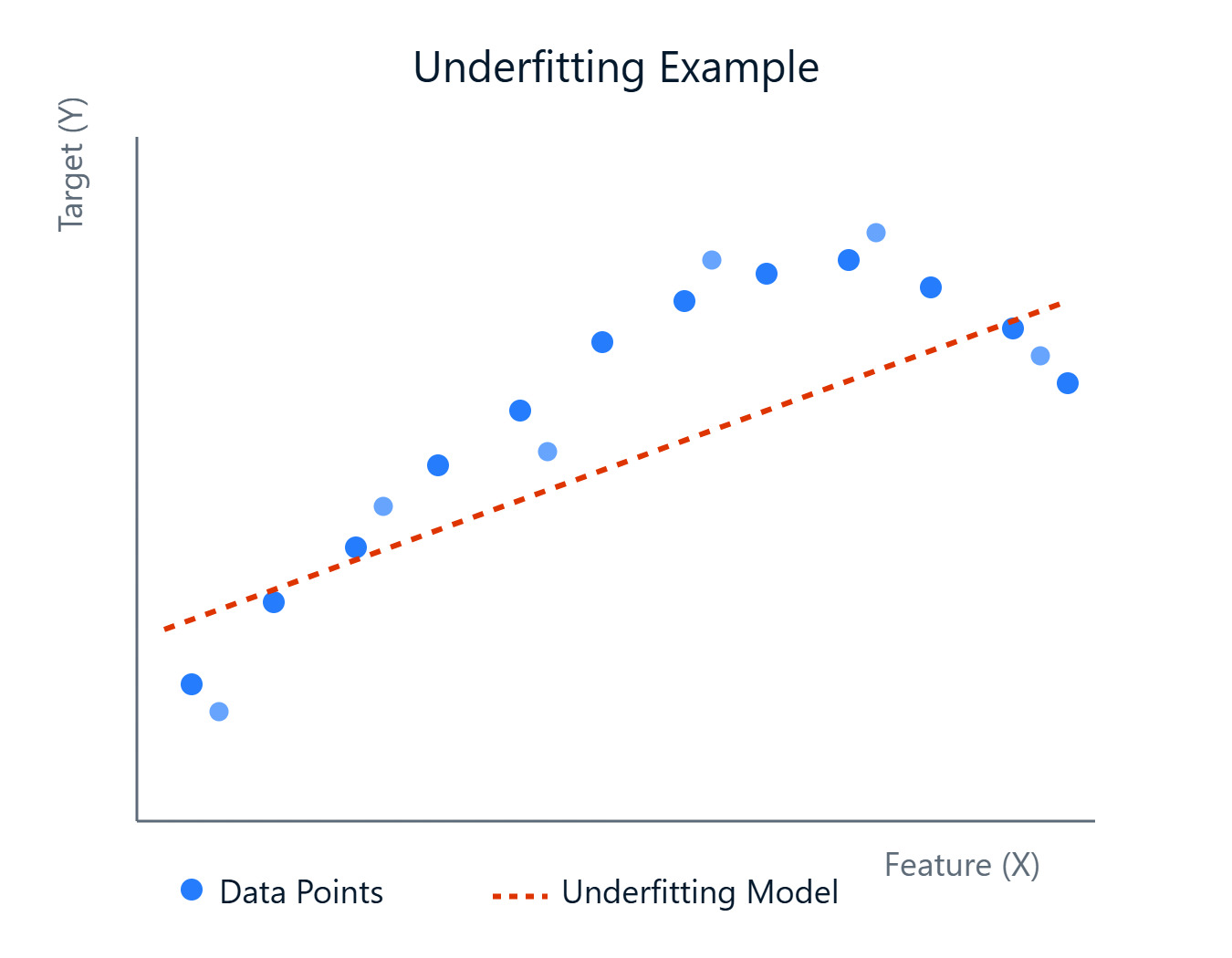
Image par l'auteur

Dans cet article, nous verrons ce qu'est l'ajustement insuffisant, pourquoi il se produit, comment le repérer et, surtout, comment y remédier. Si vous souhaitez vous familiariser avec l'apprentissage automatique, n'hésitez pas à consulter notre cours sur l'apprentissage automatique (Machine Learning Fundamentals in Python). Cours sur les principes fondamentaux de l'apprentissage automatique en Python.

Qu'est-ce que l'ajustement insuffisant ?

Examinons plus en détail le concept d'underfitting et comment il s'oppose à son pendant, l'overfitting. La compréhension de cette distinction est fondamentale pour le diagnostic et l'amélioration des modèles.

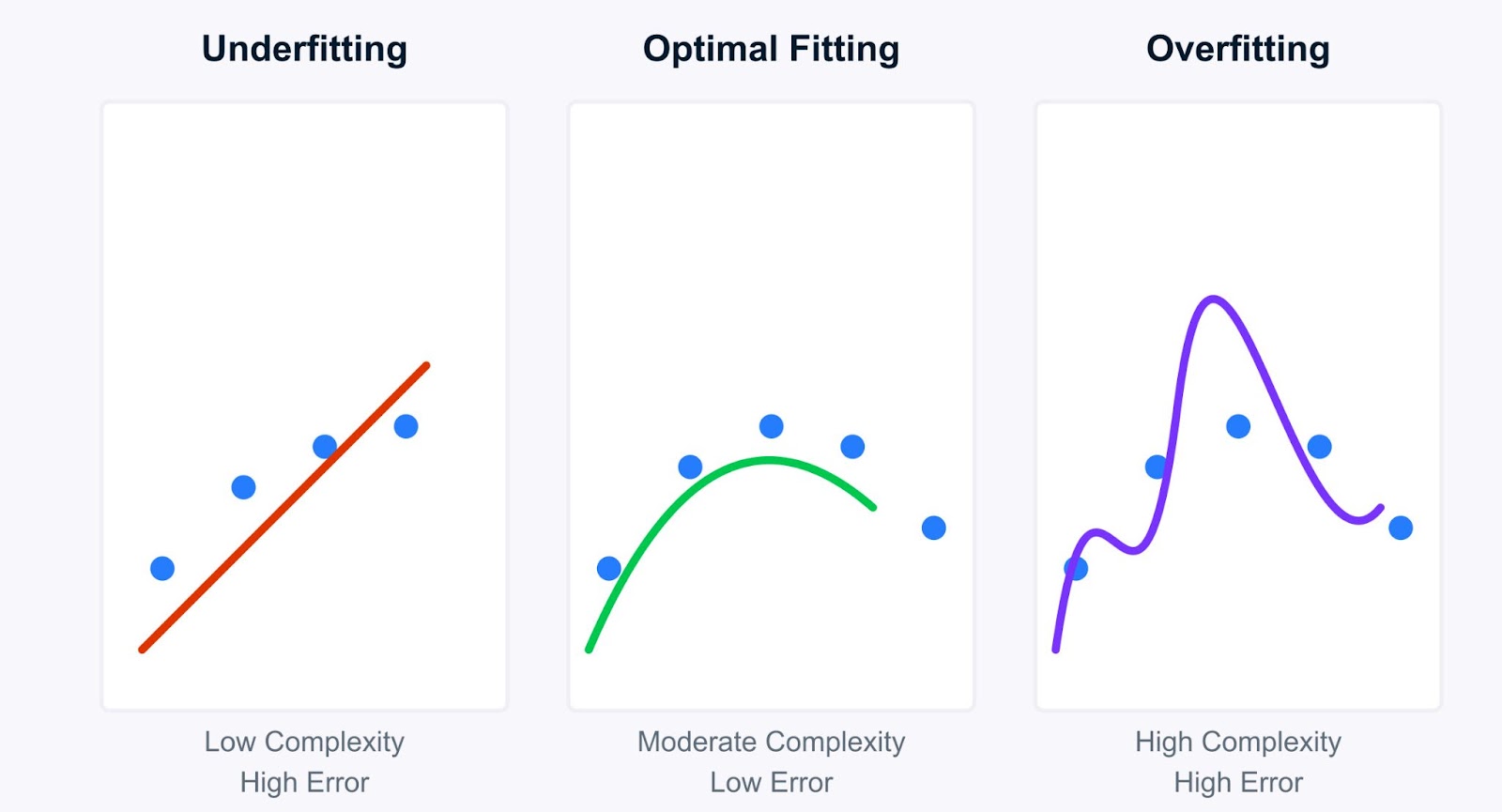
Image par l'auteur

En termes simples, il y a sous-adaptation lorsqu'un modèle d'apprentissage automatique est trop simple pour capturer les modèles sous-jacents dans les données d'apprentissage. Imaginez que vous essayez d'ajuster une ligne droite à des points de données qui suivent clairement une courbe, et que la ligne (notre modèle) n'est tout simplement pas assez complexe. Un modèle sous-adapté souffre d'un biais important, ce qui signifie qu'il émet des hypothèses fortes sur les données (par exemple, en supposant une relation linéaire alors qu'il n'y en a pas). 

Comme il n'apprend pas bien les données, il obtient de mauvais résultats non seulement sur les données d'apprentissage, mais aussi sur de nouvelles données inédites (données de test). Cependant, ces modèles ont tendance à avoir une faible variance, ce qui signifie que leurs prédictions ne changent pas beaucoup si vous les entraînez sur différents sous-ensembles de données. Cette simplicité les rend cohérents, bien que constamment erronés.

D'un point de vue mathématique, il s'agit de la décomposition biais-variance de l'erreur attendue du modèle. L'erreur attendue d'un modèle peut être décomposée en trois composantes : le biais au carré, la variance et l'erreur irréductible :

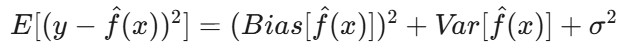
Où ?

• E[(y - f̂(x))²] est l'erreur quadratique attendue de la prédiction.

• Bias(f̂(x)) mesure l'erreur introduite par l'approximation de la fonction réelle f(x) avec le modèle.

• Var(f̂(x)) est la variabilité de la prédiction du modèle pour différents ensembles de données d'apprentissage.

• σ² représente l'erreur irréductible - le bruit inhérent aux données qui ne peut être prédit.

Dans le cas d'un sous-ajustement, le termeBias(f̂(x)) domine l'erreur. Le modèle est trop simple, ce qui entraîne des erreurs systématiques et ne permet pas de saisir la véritable relation entre les données.

Contraste entre sous-adaptation et suradaptation

La compréhension de l'underfitting devient plus claire lorsqu'on la compare à celle de l'overfitting. Si les modèles sous-adaptés sont trop simples, les modèles suradaptés sont trop complexes. Ils apprennenttrop bien les données d'apprentissage , en saisissant non seulement les modèles sous-jacents, mais aussi le bruit et les fluctuations aléatoires.

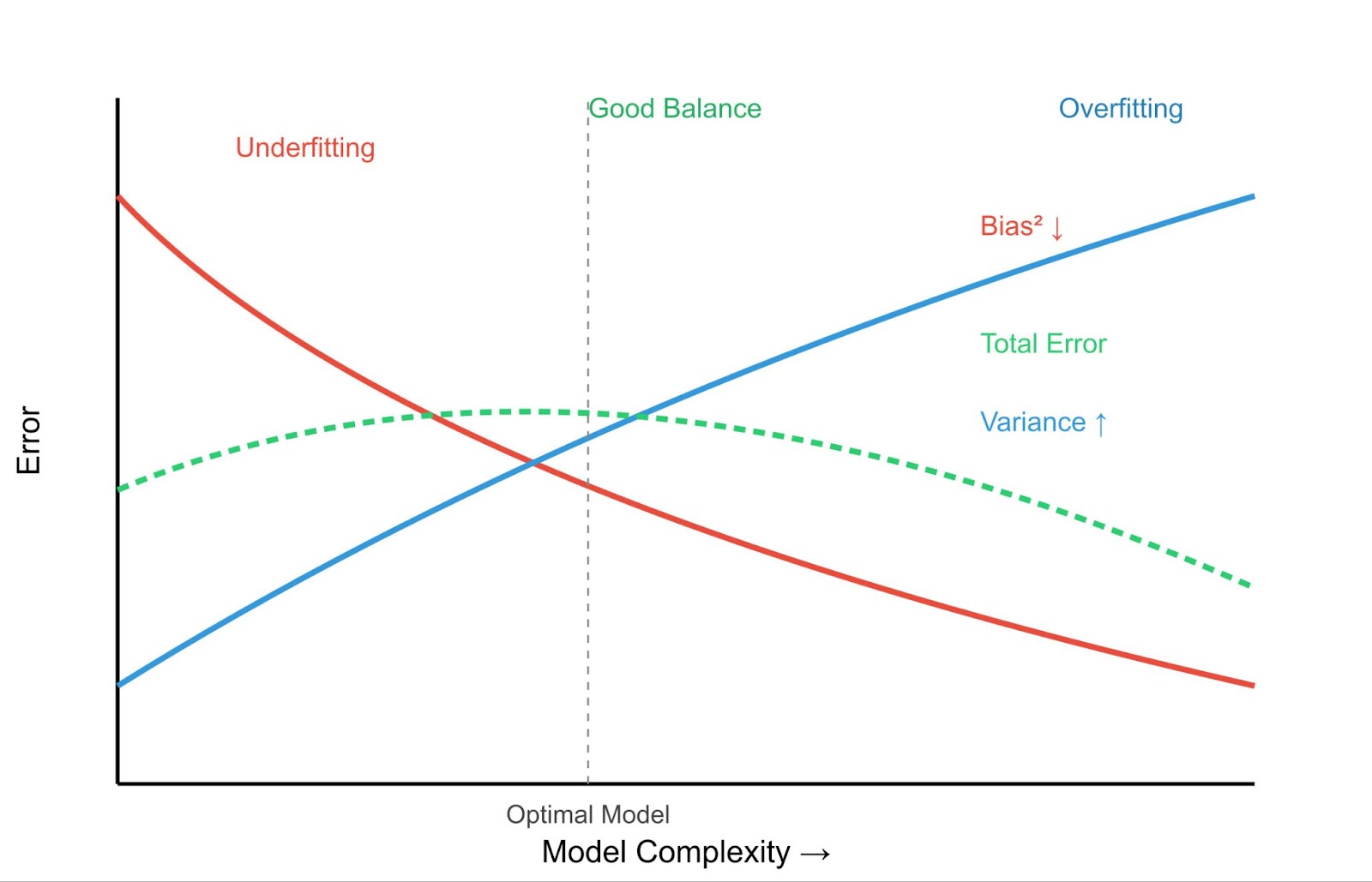
Compromis entre le biais et la variance - Image par l'auteur

Examinons les principales différences entre l'ajustement insuffisant et l'ajustement excessif :

Cela conduit au concept crucial du compromis biais-variance.

• Biais élevé (sous-adaptation) : Les modèles simples ont un biais élevé mais une faible variance. Ils sont systématiquement erronés, mais ne varient pas beaucoup en fonction des données d'entraînement.
• Variance élevée (surajustement) : Les modèles complexes ont un faible biais mais une variance élevée. Ils s'adaptent très bien aux données d'apprentissage (faible biais) mais sont très sensibles aux données d'apprentissage spécifiques utilisées, ce qui entraîne une mauvaise généralisation sur de nouvelles données. Vous pouvez en savoir plus à ce sujet dans notre article Qu'est-ce que l'overfitting ?.

L'objectif est de trouver le juste milieu : un modèle suffisamment complexe pour capturer les vrais modèles (faible biais), mais pas trop complexe pour apprendre le bruit (faible variance).

Exemples :

• Exemple de sous-adaptation : Essayer de prédire les prix des maisons, qui dépendent de la taille, de l'emplacement, de l'âge, etc., en utilisant uniquement le nombre de pièces. Le modèle est trop simple (biais important) et les prévisions seront probablement médiocres pour la plupart des maisons.
• Exemple de surajustement : Création d'un modèle de régression polynomiale très complexe qui passe parfaitement par chaque point de données de votre ensemble de formation sur le prix des maisons. Ce modèle peut avoir une erreur proche de zéro sur les données d'apprentissage, mais ses performances seront terribles sur les nouvelles maisons parce qu'il a appris le bruit spécifique à l'ensemble d'apprentissage (variance élevée).

Il est important de comprendre où se situe votre modèle dans ce spectre pour développer des solutions d'apprentissage automatique efficaces, comme nous le verrons dans les sections suivantes consacrées à la détection et à la résolution des problèmes d'ajustement insuffisant.

Causes de l'inadaptation et indicateurs de diagnostic

Maintenant que nous avons compris ce qu'est l'ajustement insuffisant, voyons pourquoi il se produit et comment vous pouvez le détecter dans vos propres projets. L'identification de la cause première est essentielle pour choisir la bonne stratégie d'atténuation. 

Principales causes de l'inadaptation

Plusieurs facteurs peuvent conduire à un modèle sous-adapté :

Complexité insuffisante du modèle

L'algorithme choisi peut être trop simple pour la structure sous-jacente des données. Par exemple, l'utilisation d'un modèle de régression linéaire lorsque la relation entre les caractéristiques et la variable cible est fortement non linéaire. Le modèle n'est pas en mesure d'appréhender ces complexités.

Formation inadéquate

Le modèle peut ne pas avoir été entraîné suffisamment longtemps (par exemple, trop peu d'époques dans les réseaux neuronaux) ou avec des paramètres d'apprentissage appropriés. Si le processus de formation s'arrête prématurément, le modèle n'aura pas eu suffisamment d'occasions d'apprendre les modèles, même s'il en a la capacité.

Mauvaise représentation des caractéristiques 

Les caractéristiques utilisées pour former le modèle peuvent ne pas représenter correctement les facteurs sous-jacents qui influencent la variable cible. Cela pourrait signifier :

• Il manque des fonctionnalités importantes : Des prédicteurs clés n'ont pas été inclus dans l'ensemble de données.
• Caractéristiques non pertinentes : L'ensemble de données contient du bruit ou des caractéristiques qui ne sont pas en corrélation avec le résultat, ce qui peut induire en erreur un modèle simple.
• Caractéristiques nécessitant une transformation : Les caractéristiques peuvent nécessiter une mise à l'échelle, une normalisation ou un codage (par exemple, variables catégorielles) pour être utiles au modèle.

Régularisation excessive

Les techniques de régularisation (comme les pénalités L1 ou L2) sont principalement utilisées pour éviter l'ajustement excessif en ajoutant une pénalité pour la complexité. Toutefois, si la force de régularisation (par exemple, le paramètre lambda) est trop élevée, elle peut pénaliser excessivement le modèle, le forçant à devenir trop simple et provoquant ainsi un sous-ajustement. Pour en savoir plus sur la régularisation, consultez le site Towards Preventing Overfitting in Machine Learning (en anglais) : Régularisation.

Données de faible qualité ou insuffisantes

• Pas assez de données : Si l'ensemble de données d'apprentissage est trop petit, le modèle risque de ne pas avoir suffisamment d'exemples pour apprendre efficacement les modèles sous-jacents.
• Bruit élevé : Si les données sont très bruyantes, le modèle peut avoir du mal à distinguer le signal du bruit, surtout s'il s'agit d'un modèle simple.
• Valeurs manquantes : Des quantités importantes de données manquantes peuvent entraver la capacité d'apprentissage du modèle, en particulier si elles ne sont pas traitées correctement. Les techniques permettant de résoudre ce problème sont abordées dans le document suivant Traiter les données manquantes avec les imputations dans R.

Méthodes de détection

Comment savoir si votre modèle est sous-adapté ? Voici quelques techniques de diagnostic courantes :

Analyse des indicateurs de performance 

L'indicateur le plus évident est une performance médiocre sur les deux sites l'ensemble de formation et l'ensemble de validation/test. Si votre modèle présente un taux d'erreur élevé (ou une faible précision, un faible R au carré, etc.) sur les données sur lesquelles il a été entraîné, cela indique clairement qu'il n'a pas appris les modèles de manière efficace. Contrairement à l'overfitting, où les performances de l'entraînement sont excellentes, mais les performances des tests sont médiocres, l'underfitting présente des performances médiocres dans tous les domaines.

Courbes d'apprentissage

Le graphique des performances du modèle (par exemple, l'erreur ou la précision) sur les ensembles d'apprentissage et de validation en fonction du temps d'apprentissage ou de la taille de l'ensemble de données peut s'avérer très instructif. Pour un modèle sous-adapté, les courbes d'apprentissage montrent généralement :

• Erreur d'entraînement importante qui entraîne un plafonnement précoce.
• Erreur de validation élevée, proche de l'erreur d'apprentissage, et plafonnement.
• Les deux courbes convergent vers un niveau d'erreur élevé, ce qui indique que le modèle ne s'améliore pas de manière significative, même avec davantage de données ou d'entraînement.

Analyse des caractéristiques

Passez en revue les caractéristiques utilisées. Sont-ils pertinents ? Y a-t-il des interactions que vous n'avez pas saisies ? Les caractéristiques numériques sont-elles mises à l'échelle ? Les caractéristiques catégorielles sont-elles codées de manière appropriée ? 

Parfois, le réexamen de l'ingénierie des fonctionnalités peut révéler la raison pour laquelle le modèle est en difficulté. Les concepts de base sont couverts dans Fondamentaux de l'apprentissage automatique en R. Pour approfondir les relations statistiques, vous pouvez consulter des ressources telles que L'inférence statistique en R.

Modélisation comparative

Entraînez un modèle plus complexe (par exemple, un arbre de décision ou une machine à gradient de croissance si vous avez initialement utilisé la régression linéaire) sur les mêmes données. Si le modèle plus complexe surpasse de manière significative votre modèle initial à la fois sur les ensembles d'apprentissage et de validation, cela suggère que votre modèle initial était probablement sous-adapté en raison d'une complexité insuffisante. 

Vous pouvez suivre ces comparaisons à l'aide des outils présentés dans le siteMachine Learning Experimentation : Introduction aux poids et aux biais.

En comprenant ces causes et ces méthodes de détection, vous pouvez diagnostiquer efficacement un modèle sous-adapté et prendre des mesures pour améliorer ses performances.

Stratégies d'atténuation de l'inadéquation et meilleures pratiques

Une fois que vous avez identifié un sous-ajustement, l'étape suivante consiste à savoir comment y remédier. Heureusement, plusieurs stratégies efficaces permettent d'améliorer la capacité de votre modèle à apprendre les modèles sous-jacents des données. Examinons-en quelques-uns :

Améliorer la complexité du modèle

Si votre modèle est trop simple (biais élevé), le fait de le rendre plus complexe peut souvent résoudre le problème de l'ajustement insuffisant. Nous pouvons le faire de la manière suivante :

Sélection d'un algorithme

Passez à un modèle plus puissant. Si la régression linéaire n'est pas adaptée, essayez la régression polynomiale, les arbres de décision, les forêts aléatoires, les machines à gradient de croissance (comme XGBoost ou LightGBM), ou des machines à vecteurs de support (SVM) avec des noyaux non linéaires. Ces modèles ont par nature une plus grande capacité à saisir des relations complexes.

Expansion polynomiale des caractéristiques

Pour les problèmes de régression, vous pouvez créer des caractéristiques polynomiales à partir de vos caractéristiques numériques existantes. Cela permet aux modèles linéaires de s'adapter à des relations plus complexes et plus courbes. Par exemple, si vous avez une fonctionnalité x, vous pouvez ajouter x2, x3, etc. en tant que nouvelles fonctionnalités. Scikit-learn fournit PolynomialFeatures pour cela.

Réglage des hyperparamètres

De nombreux modèles complexes ont des hyperparamètres qui contrôlent leur complexité (par exemple, la profondeur d'un arbre de décision, le nombre de neurones dans une couche de réseau neuronal, le paramètre C dans les SVM). L'ajustement de ces hyperparamètres pour permettre une plus grande complexité peut réduire le biais. 

Des techniques telles que la recherche en grille ou la recherche aléatoire sont essentielles à cet égard. Apprenez-en plus avec des cours tels que L'optimisation des hyperparamètres en Python ou Optimisation des hyperparamètres en R. Consultez également notre tutoriel sur l'optimisation des hyperparamètres dans les modèles d'apprentissage automatique Optimisation des hyperparamètres dans les modèles d'apprentissage automatique.

Ingénierie des caractéristiques et augmentation des données

Parfois, ce n'est pas le modèle qui pose problème, mais la représentation des données. L'amélioration des caractéristiques peut être d'un grand secours. Nous pouvons le faire de la manière suivante :

Création d'éléments spécifiques à un domaine

Utilisez votre connaissance du domaine du problème pour créer de nouvelles fonctionnalités qui pourraient être plus informatives. Par exemple, pour prévoir les prix des logements, il est possible de combiner le "nombre de chambres" et le "nombre de salles de bains" en une caractéristique "nombre total de pièces", ou de calculer l'"âge du logement" à partir de l'"année de construction".

Caractéristiques de l'interaction

Créez des caractéristiques qui représentent l'interaction entre des caractéristiques existantes (par exemple, en multipliant deux caractéristiques). Cela peut aider les modèles à saisir les effets synergiques.

Enrichissement des données

Complétez votre ensemble de données par des sources de données externes si possible. Par exemple, en ajoutant des données démographiques aux informations sur les clients ou des données météorologiques aux prévisions de vente.

Augmentation des données (principalement pour les données non structurées)

Pour les images ou les données textuelles, des techniques telles que la rotation des images ou le remplacement des synonymes dans le texte peuvent augmenter artificiellement la taille et la diversité de l'ensemble d'apprentissage, ce qui peut aider le modèle à apprendre des modèles plus robustes.

Ajustement de la régularisation

Si le sous-ajustement est causé par une régularisationexcessive destinée à empêcher le surajustement, vous devez la réduire. Diminuez la valeur du paramètre de régularisation (par exemple, alpha dans Ridge/Lasso, C dans les SVM - notez que pour les SVM, un C plus petit ( ) signifie une régularisation plus forte, vous devez donc augmenter C).

Si vous utilisez l'abandon, réduisez le taux d'abandon (la fraction de neurones abandonnés pendant la formation). Un taux plus bas permet de conserver une plus grande capacité du réseau.

Trouver le bon équilibre nécessite souvent un réglage minutieux, ce qui souligne à nouveau l'importance de l'optimisation des hyperparamètres.

Méthodes d'ensemble

Les méthodes d'ensemble combinent les prédictions de plusieurs modèles individuels (apprenants faibles) pour produire une prédiction finale plus forte et plus robuste. Ils sont souvent très efficaces pour réduire à la fois les biais et la variance. Voici quelques-unes des méthodes d'ensemble :

• Bagging (par exemple, Random Forests): Entraîne plusieurs modèles (par exemple, des arbres de décision) indépendamment sur différents échantillons bootstrap des données et fait la moyenne de leurs prédictions. Cela réduit principalement la variance, mais peut également être utile si les apprenants de base sont légèrement biaisés. Consultez notre Tutoriel sur l'ensachage pour plus d'informations.
• Boosting (par exemple, AdaBoost, Gradient Boosting): Entraîne les modèles de manière séquentielle, chaque nouveau modèle s'attachant à corriger les erreurs commises par les précédents. Le boosting est particulièrement efficace pour réduire les biais et transformer les apprenants faibles en apprenants forts, ce qui en fait un outil puissant contre le sous-ajustement. Nous disposons d'un . Guide de dynamisation pour en savoir plus.
• Empilage: Entraîne plusieurs types de modèles différents et utilise ensuite un autre modèle (un méta-apprenant) pour apprendre à combiner au mieux leurs prédictions.

En appliquant ces stratégies, souvent en les combinant, vous pouvez remédier efficacement à l'insuffisance d'ajustement et construire des modèles qui capturent mieux les complexités de vos données.

Applications pratiques et études de cas

Le fait de voir l'ajustement insuffisant en action avec des ensembles de données et du code peut clarifier le concept de manière significative. Prenons des exemples pratiques pour montrer comment se comporte un modèle sous-adapté et comment ses performances peuvent être améliorées.

Exemple d'ajustement insuffisant de la régression linéaire

Un scénario courant de sous-adaptation se produit lorsqu'un modèle linéaire simple est utilisé pour décrire une relation non linéaire. Illustrons cela en essayant d'ajuster un modèle de régression linéaire à des données qui suivent un schéma quadratique.

Nous allons générer des données synthétiques où la variable cible y a une relation quadratique avec une caractéristique X. Tout d'abord, nous allons mettre en place un modèle de régression linéaire simple. Nous observerons ses piètres performances (erreur quadratique moyenne élevée - EQM) et nous verrons comment il ne parvient pas à capturer la courbe des données. 

Ensuite, nous étendrons les caractéristiques en ajoutant un terme polynomial et nous ajusterons un modèle de régression polynomiale. Cela démontrera comment l'augmentation de la complexité du modèle peut réduire les biais et améliorer de manière significative la précision du modèle.

Commençons par importer les bibliothèques nécessaires comme suit :

# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_error

Générons des données synthétiques non linéaires. Nous allons créer des données avec une relation quadratique : y = 0,5*X^2 + X + 2 + bruit.

np.random.seed(42) # for reproducibility
num_samples = 100
X = np.sort(10 * np.random.rand(num_samples, 1) - 5, axis=0) # Feature X (sorted for plotting)
y_true = 0.5 * X**2 + X + 2 # True quadratic relationship
y = y_true + np.random.randn(num_samples, 1) * 5 # Add some noise to make it realistic

Nous allons maintenant ajuster un modèle de régression linéaire simple (Underfitting Model) comme indiqué ci-dessous :

linear_model = LinearRegression()
linear_model.fit(X, y)
y_pred_linear = linear_model.predict(X)
mse_linear = mean_squared_error(y, y_pred_linear)

print(f"--- Simple Linear Regression (Potential Underfitting Model) ---")
print(f"Mean Squared Error (MSE): {mse_linear:.2f}")
print(f"Model Coefficients (slope): {linear_model.coef_[0][0]:.2f}")
print(f"Model Intercept: {linear_model.intercept_[0]:.2f}")

Sortie :

--- Simple Linear Regression (Potential Underfitting Model) ---

Mean Squared Error (MSE): 34.03

Model Coefficients (slope): 1.00

Model Intercept: 6.42

Nous allons maintenant ajuster un modèle de régression polynomiale (modèle amélioré). Pour ce faire, nous créons des caractéristiques polynomiales (degré 2), puis nous adaptons un modèle linéaire à ces caractéristiques. L'étape PolynomialFeatures ajoute de nouvelles fonctionnalités. L' étape LinearRegression comporte des coefficients pour chacun d'entre eux.

Pour le degré 2, nous attendons des coefficients pour X et X^2. Une canalisation rend ce processus plus propre. L' attribut named_steps du pipeline permet d'accéder à des étapes individuelles, comme indiqué ci-dessous :

polynomial_model = make_pipeline(PolynomialFeatures(degree=2, include_bias=False), LinearRegression())
polynomial_model.fit(X, y)
y_pred_poly = polynomial_model.predict(X)
mse_poly = mean_squared_error(y, y_pred_poly)

print(f"\n--- Polynomial Regression (Degree 2) ---")
print(f"Mean Squared Error (MSE): {mse_poly:.2f}")
poly_reg_coeffs = polynomial_model.named_steps['linearregression'].coef_[0]
poly_reg_intercept = polynomial_model.named_steps['linearregression'].intercept_[0]
print(f"Model Coefficients (for X, X^2): {poly_reg_coeffs[0]:.2f}, {poly_reg_coeffs[1]:.2f}")
print(f"Model Intercept: {poly_reg_intercept:.2f}")

Sortie :

--- Polynomial Regression (Degree 2) ---

Mean Squared Error (MSE): 20.48

Model Coefficients (for X, X^2): 1.13, 0.50

Model Intercept: 2.04

Visualisons maintenant l'ajustement du modèle comme indiqué ci-dessous :

# Visualization
plt.figure(figsize=(10, 4))
plt.scatter(X, y, s=30, label="Actual Data Points", alpha=0.7, edgecolors='k')
plt.plot(X, y_pred_linear, color='red', linewidth=2, label=f'Linear Fit (Underfitting)\nMSE: {mse_linear:.2f}')
plt.plot(X, y_pred_poly, color='green', linewidth=2, label=f'Polynomial Fit (Degree 2)\nMSE: {mse_poly:.2f}')
plt.title('Demonstrating Underfitting with Linear vs. Polynomial Regression', fontsize=16)
plt.xlabel('Feature X', fontsize=14)
plt.ylabel('Target y', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()

Sortie :

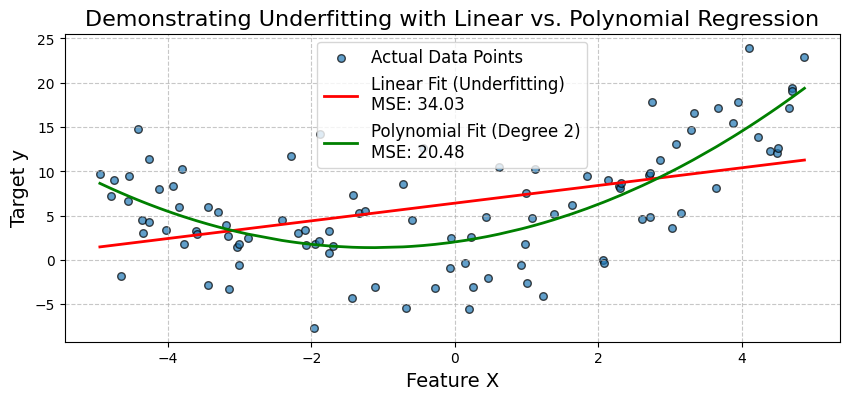
Le graphique confirme visuellement l'inadéquation du modèle linéaire simple. Elle ne permet pas de saisir la courbe dans les données. Le modèle de régression polynomiale, en incorporant le terme X^2, offre une bien meilleure adéquation, comme le montre son MSE inférieur.

Cela montre comment l'expansion des caractéristiques (augmentation de la complexité du modèle) peut réduire les biais et améliorer la précision lorsque la relation sous-jacente n'est pas linéaire. Examinons ensuite une étude de cas portant sur un diagnostic médical.

Étude de cas sur le diagnostic médical

Simulons un scénario de diagnostic médical en utilisant l'ensemble de données bien connu Breast Cancer Wisconsin (Diagnostic) disponible sur scikit-learn.

Nous allons d'abord tenter de construire un modèle de classification en n'utilisant qu'un sous-ensemble très limité de caractéristiques, ce qui pourrait conduire à un sous-ajustement. Ensuite, nous utiliserons un ensemble plus complet de caractéristiques et potentiellement un algorithme plus complexe pour démontrer l'amélioration.

Commençons par importer les bibliothèques nécessaires comme suit :

# Import necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, roc_auc_score, confusion_matrix, ConfusionMatrixDisplay

Maintenant, chargeons et préparons les données :

cancer = load_breast_cancer()
X = pd.DataFrame(cancer.data, columns=cancer.feature_names)
y = cancer.target # 0 for malignant, 1 for benign

À titre de démonstration, sélectionnons un sous-ensemble très limité de caractéristiques pour le scénario de sous-adaptation. Ces éléments ne sont peut-être pas les plus prédictifs en soi :

features_limited = ['mean texture', 'mean symmetry']
X_limited = X[features_limited]

Pour le modèle amélioré, nous utiliserons un sous-ensemble plus important (ou toutes les caractéristiques). Choisissons les dix premières caractéristiques pour obtenir un ensemble plus complet :

features_comprehensive = cancer.feature_names[:10]
X_comprehensive = X[features_comprehensive]

Divisons les données. Pour plus de clarté, nous le ferons séparément pour chaque ensemble de fonctionnalités :

X_train_lim, X_test_lim, y_train, y_test = train_test_split(X_limited, y, test_size=0.3, random_state=42, stratify=y)
X_train_comp, X_test_comp, _, _ = train_test_split(X_comprehensive, y, test_size=0.3, random_state=42, stratify=y) # y_train and y_test are the same

Échelonnons les caractéristiques, car cela est important pour la régression logistique et de nombreux autres algorithmes :

scaler_lim = StandardScaler().fit(X_train_lim)
X_train_lim_scaled = scaler_lim.transform(X_train_lim)
X_test_lim_scaled = scaler_lim.transform(X_test_lim)

scaler_comp = StandardScaler().fit(X_train_comp)
X_train_comp_scaled = scaler_comp.transform(X_train_comp)
X_test_comp_scaled = scaler_comp.transform(X_test_comp)

Maintenant, ajustons une régression logistique avec des caractéristiques limitées :

print("Scenario 1: Logistic Regression (Limited Features - Potential Underfitting)")
log_reg_limited = LogisticRegression(random_state=42, solver='liblinear') # liblinear is good for small datasets
log_reg_limited.fit(X_train_lim_scaled, y_train)
y_pred_lim = log_reg_limited.predict(X_test_lim_scaled)
y_proba_lim = log_reg_limited.predict_proba(X_test_lim_scaled)[:, 1]

acc_lim = accuracy_score(y_test, y_pred_lim)
auc_lim = roc_auc_score(y_test, y_proba_lim)
print(f"Features used: {features_limited}")
print(f"Accuracy: {acc_lim:.4f}")
print(f"AUC: {auc_lim:.4f}")

Sortie :

Scenario 1: Logistic Regression (Limited Features - Potential Underfitting)

Features used: ['mean texture', 'mean symmetry']

Accuracy: 0.7544

AUC: 0.8151

Adoptons une stratégie d'atténuation. Nous allons ajuster un modèle de régression logistique avec plus de caractéristiques :

print("Scenario 2: Logistic Regression (Comprehensive Features)")
log_reg_comp = LogisticRegression(random_state=42, solver='liblinear')
log_reg_comp.fit(X_train_comp_scaled, y_train)
y_pred_comp_lr = log_reg_comp.predict(X_test_comp_scaled)
y_proba_comp_lr = log_reg_comp.predict_proba(X_test_comp_scaled)[:, 1]

acc_comp_lr = accuracy_score(y_test, y_pred_comp_lr)
auc_comp_lr = roc_auc_score(y_test, y_proba_comp_lr)
print(f"Features used: First 10 features") # For brevity
print(f"Accuracy: {acc_comp_lr:.4f}")
print(f"AUC: {auc_comp_lr:.4f}")

Sortie :

Scenario 2: Logistic Regression (Comprehensive Features)

Features used: First 10 features

Accuracy: 0.9181

AUC: 0.9831

Maintenant, adaptons un modèle plus complexe comme Random Forest avec plus de caractéristiques :

print("Scenario 3: Random Forest (Comprehensive Features)")
rf_comp = RandomForestClassifier(random_state=42, n_estimators=100) # n_estimators is a key hyperparameter
rf_comp.fit(X_train_comp_scaled, y_train) # RF can also benefit from scaled data, though less sensitive
y_pred_comp_rf = rf_comp.predict(X_test_comp_scaled)
y_proba_comp_rf = rf_comp.predict_proba(X_test_comp_scaled)[:, 1]

acc_comp_rf = accuracy_score(y_test, y_pred_comp_rf)
auc_comp_rf = roc_auc_score(y_test, y_proba_comp_rf)
print(f"Features used: First 10 features")
print(f"Accuracy: {acc_comp_rf:.4f}")
print(f"AUC: {auc_comp_rf:.4f}")

Sortie :

Scenario 3: Random Forest (Comprehensive Features)

Features used: First 10 features

Accuracy: 0.9415

AUC: 0.9878

Graphiquez et comparez la matrice de confusion pour chaque cas :

fig, axes = plt.subplots(1, 3, figsize=(20, 5))
fig.suptitle('Comparison of Model Performance (Confusion Matrices on Test Set)', fontsize=16)

# Model 1: Logistic Regression (Limited Features)
cm_lim = confusion_matrix(y_test, y_pred_lim)
disp_lim = ConfusionMatrixDisplay(confusion_matrix=cm_lim, display_labels=cancer.target_names)
disp_lim.plot(ax=axes[0], cmap='Blues')
axes[0].set_title(f'LogReg (Limited Features)\nAcc: {acc_lim:.2f}, AUC: {auc_lim:.2f}')

# Model 2: Logistic Regression (Comprehensive Features)
cm_comp_lr = confusion_matrix(y_test, y_pred_comp_lr)
disp_comp_lr = ConfusionMatrixDisplay(confusion_matrix=cm_comp_lr, display_labels=cancer.target_names)
disp_comp_lr.plot(ax=axes[1], cmap='Greens')
axes[1].set_title(f'LogReg (Comprehensive Features)\nAcc: {acc_comp_lr:.2f}, AUC: {auc_comp_lr:.2f}')

# Model 3: Random Forest (Comprehensive Features)
cm_comp_rf = confusion_matrix(y_test, y_pred_comp_rf)
disp_comp_rf = ConfusionMatrixDisplay(confusion_matrix=cm_comp_rf, display_labels=cancer.target_names)
disp_comp_rf.plot(ax=axes[2], cmap='Oranges')
axes[2].set_title(f'Random Forest (Comprehensive Features)\nAcc: {acc_comp_rf:.2f}, AUC: {auc_comp_rf:.2f}')

plt.tight_layout(rect=[0, 0, 1, 0.96]) # Adjust layout to make space for suptitle
plt.show()

Sortie :

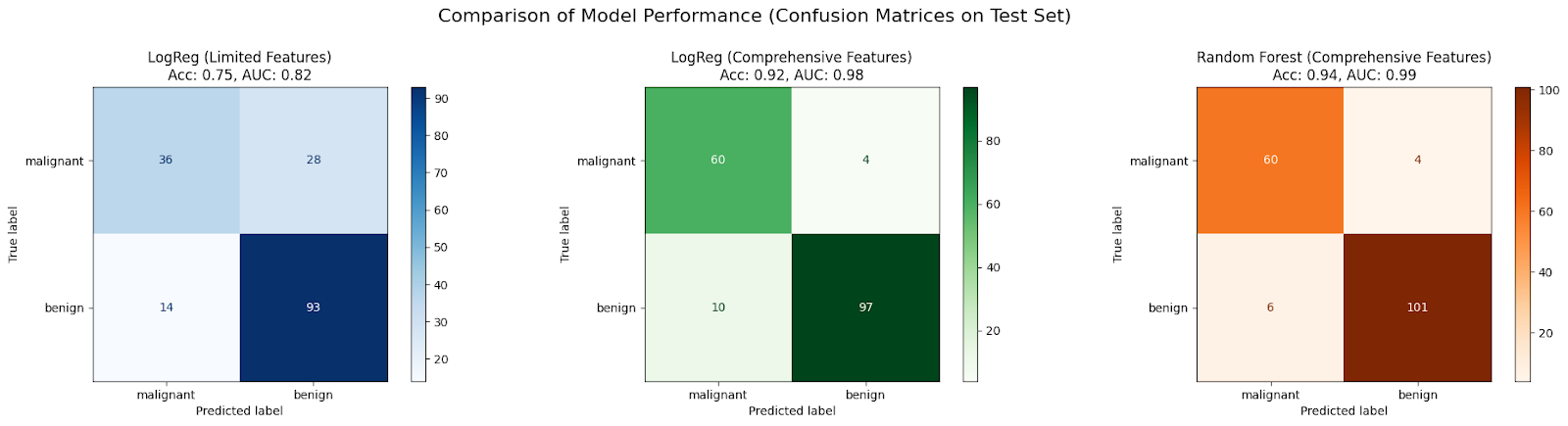
Dans cette étude de cas, un modèle initial LogisticRegression formé sur seulement deux caractéristiques (scénario 1) devrait être sous-adapté en raison d'informations insuffisantes, ce qui se traduit par une précision et une SSC médiocres.

Les performances s'améliorent généralement lorsque le même algorithme se voit attribuer un ensemble plus complet de caractéristiques (scénario 2), car il dispose de plus de données pour apprendre, ce qui réduit les biais.

L'utilisation d'un algorithme plus complexe tel que RandomForestClassifier avec l'ensemble complet de caractéristiques (scénario 3) permet souvent d'obtenir une amélioration supplémentaire, car il peut capturer les non-linéarités et les interactions des caractéristiques de manière plus efficace, ce qui réduit encore le biais et améliore l'adéquation du modèle aux données.

Sujets avancés et orientations futures

Bien que nous ayons abordé les principes fondamentaux, le paysage de l'apprentissage automatique est en constante évolution. Voici un bref aperçu de la manière dont l'adaptation insuffisante est liée à des domaines plus avancés.

Le rôle de l'apprentissage profond

Les modèles d'apprentissage profond, en particulier les réseaux neuronaux profonds à plusieurs couches, sont connus pour leur grande capacité, ce qui signifie qu'ils peuvent théoriquement approximer des fonctions très complexes.

En raison de leur complexité inhérente, les modèles d'apprentissage profond sont généralement moins sujets à un sous-ajustement que les modèles plus simples, à condition qu'ils soient formés correctement sur un nombre suffisant de données. Leur structure leur permet d'apprendre automatiquement des représentations complexes de caractéristiques à partir de données brutes (comme des pixels dans des images ou des mots dans un texte).

Cependant, l'apprentissage profond n'est pas à l'abri de problèmes qui ressemblent à à un sous-ajustement. Si un réseau est mal conçu (par exemple, profondeur/largeur insuffisante pour la tâche), s'il n'est pas entraîné suffisamment longtemps ou s'il utilise des fonctions d'activation ou des algorithmes d'optimisation inappropriés, il peut toujours ne pas converger et présenter une erreur d'apprentissage élevée.

Les innovations architecturales telles que les connexions résiduelles (ResNets) et les techniques de normalisation (Batch Normalization) permettent d'entraîner efficacement les réseaux très profonds, en atténuant les problèmes de gradient d'évanouissement/explosion et en leur permettant d'atteindre leur pleine capacité, évitant ainsi les problèmes de convergence qui imitent l'insuffisance d'ajustement.

Apprentissage automatique des machines (AutoML)

Trouver le bon modèle, les bonnes caractéristiques et les bons hyperparamètres pour éviter à la fois l'underfitting et l'overfitting peut prendre beaucoup de temps. AutoML vise à automatiser ce processus.

Les cadres AutoML peuvent explorer automatiquement différents types de modèles (des modèles linéaires aux ensembles complexes et aux réseaux neuronaux), effectuer l'ingénierie et la sélection des caractéristiques et optimiser les hyperparamètres. En recherchant systématiquement un vaste espace de possibilités, AutoML peut identifier des configurations de modèles suffisamment complexes pour ne pas sous-adapter les données.

Des méthodes telles que la recherche d'architecture neuronale (NAS) conçoivent automatiquement des architectures de réseau, tandis que des techniques sophistiquées d'optimisation des hyperparamètres (par exemple, l'optimisation bayésienne) permettent de trouver efficacement de bonnes configurations d'hyperparamètres. Ces outils peuvent accélérer considérablement le processus de recherche d'un modèle bien adapté, en réduisant les efforts manuels nécessaires pour diagnostiquer et corriger un modèle sous-adapté.

Conclusion

Comprendre le dilemme entre l'ajustement insuffisant et l'ajustement excessif est fondamental pour la réussite de l'apprentissage automatique. Nous avons vu que le sous-ajustement survient lorsqu'un modèle est trop simple (biais élevé) pour capturer les tendances sous-jacentes des données, ce qui entraîne de mauvaises performances à la fois sur les données d'apprentissage et sur les données non vues. Les principales causes sont une complexité insuffisante du modèle, des caractéristiques médiocres, une formation inadéquate et une régularisation excessive.

Pour diagnostiquer un sous-ajustement, il faut examiner les mesures de performance, tracer les courbes d'apprentissage et comparer les modèles, souvent à l'aide d'un code. Heureusement, nous disposons de plusieurs stratégies pour remédier à l'insuffisance d'ajustement : augmentation de la complexité du modèle (choix de meilleurs algorithmes, expansion des caractéristiques, réglage des hyperparamètres), amélioration des caractéristiques (ingénierie des caractéristiques, enrichissement des données), ajustement de la régularisation et utilisation de méthodes d'ensemble puissantes, comme le démontrent nos exemples de code.

Pour vous familiariser avec ces techniques et d'autres exemples pratiques, consultez notre parcours de compétences Le cursus Machine Learning Fundamentals in Python (Apprentissage automatique en Python).