¿Qué es la inadaptación? Cómo detectar y superar un sesgo elevado en los modelos ML

A medida que construyamos modelos para predecir resultados o descubrir patrones, nos encontraremos con diversos retos. Un obstáculo común es crear un modelo que capte con precisión las tendencias subyacentes en tus datos. A veces, los modelos son demasiado simples y no consiguen aprender las complejidades, lo que conduce a un rendimiento deficiente. Este fenómeno se conoce como infraajuste.

Un modelo con un ajuste insuficiente no sólo funciona mal con los datos con los que se ha entrenado, sino que tampoco generaliza a datos nuevos que no se han visto. Esto significa que tus predicciones podrían ser poco fiables en situaciones reales. Reconocer y abordar la inadaptación es un paso importante para construir modelos de machine learning sólidos y eficaces. 

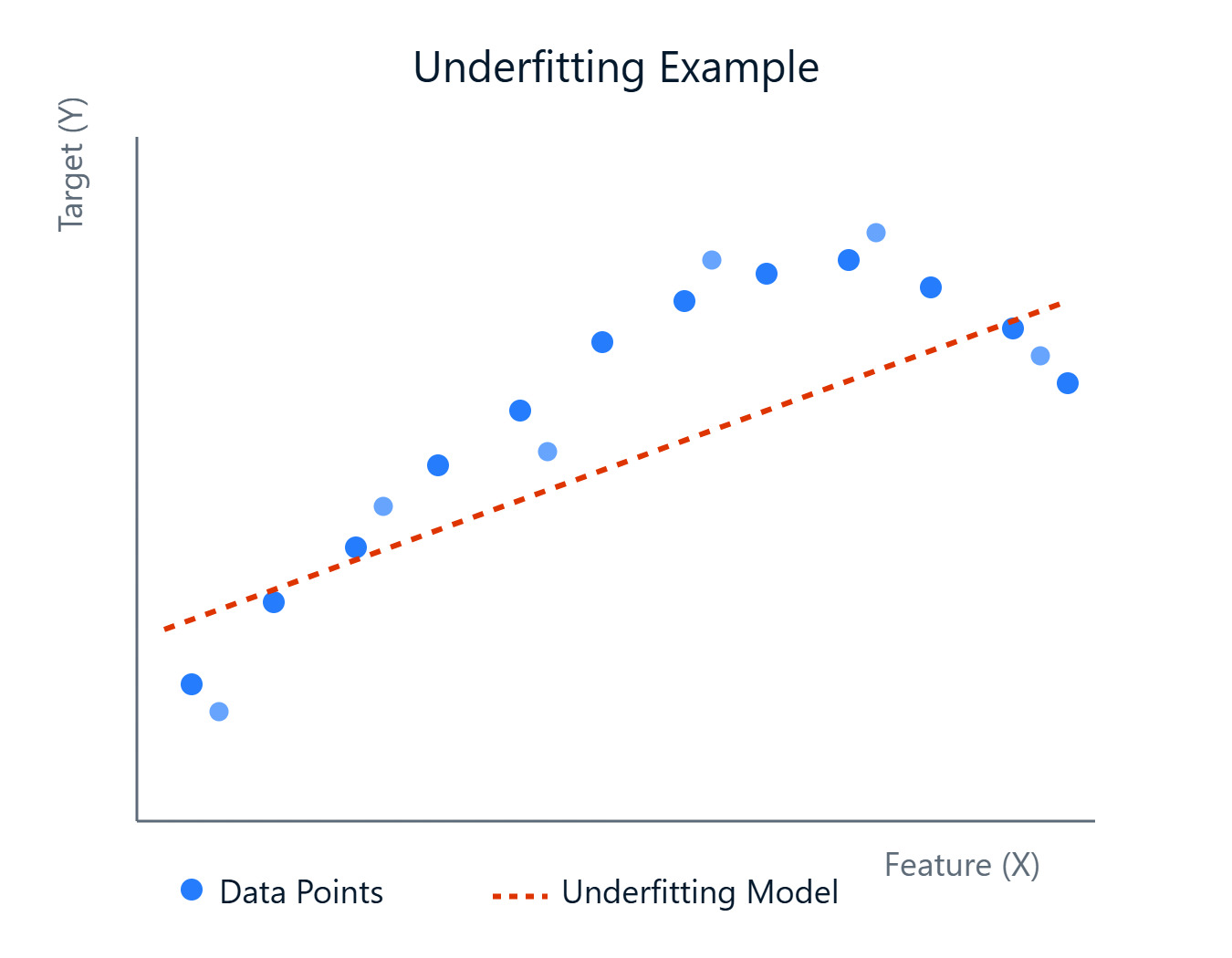
Imagen del autor

En este artículo veremos qué es la inadaptación, por qué se produce, cómo detectarla y, lo más importante, cómo solucionarla. Si quieres ponerte manos a la obra con el machine learning, asegúrate de echar un vistazo a nuestro curso Programa de Fundamentos de Machine Learning en Python.

¿Qué es la inadaptación?

Profundicemos en el concepto de infraadaptación y cómo contrasta con su contrapartida, la sobreadaptación. Comprender esta distinción es fundamental para el diagnóstico y la mejora de los modelos.

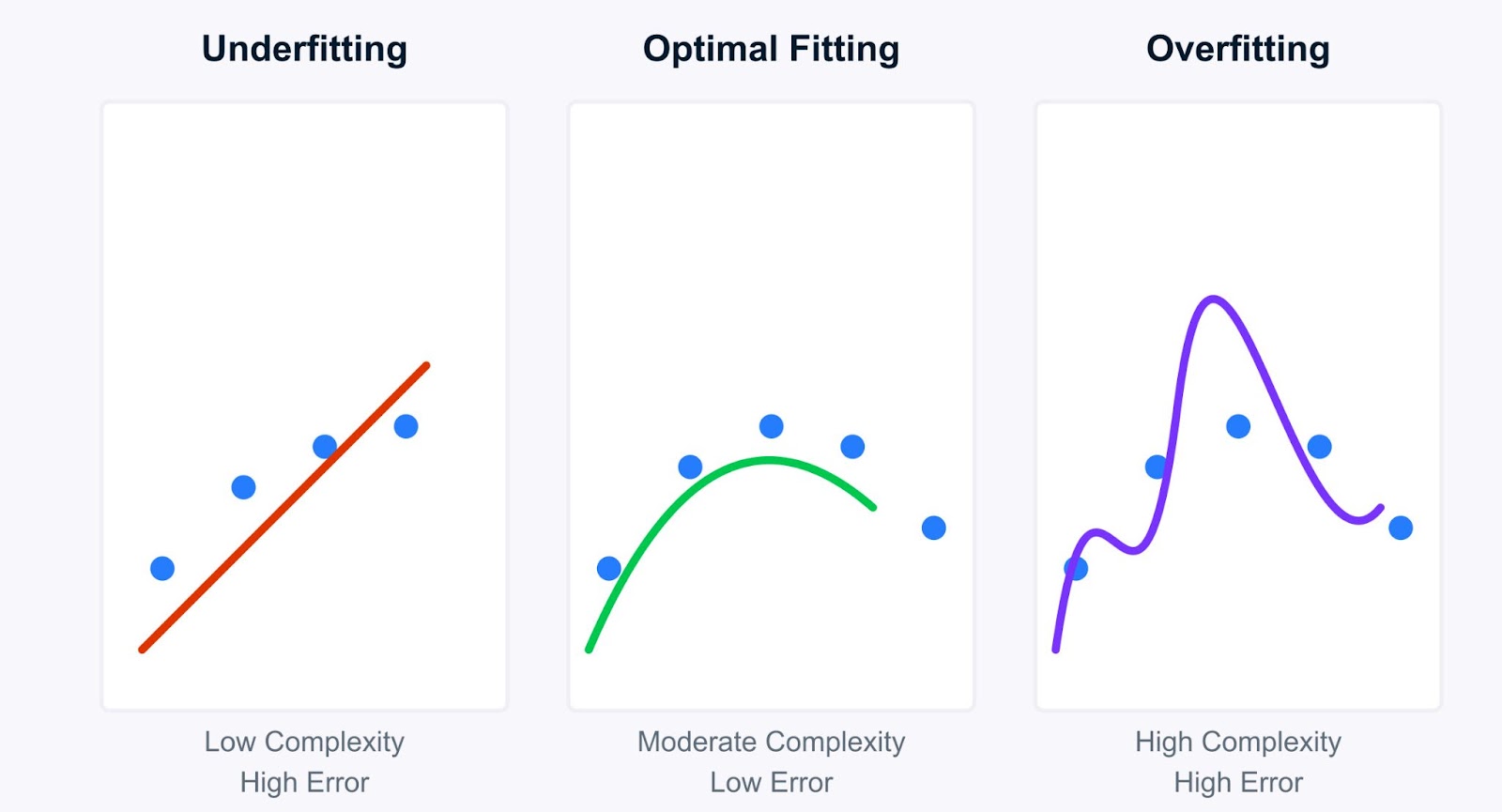
Imagen del autor

En pocas palabras, el infraajuste se produce cuando un modelo de machine learning es demasiado simple para captar los patrones subyacentes en los datos de entrenamiento. Imagina que intentas ajustar una línea recta a través de puntos de datos que siguen claramente una curva, y la línea (nuestro modelo) no es lo bastante compleja. Un modelo con un ajuste insuficiente tiene un sesgo elevado, lo que significa que hace suposiciones fuertes sobre los datos (por ejemplo, asumir una relación lineal cuando no la hay). 

Como no aprende bien los datos, su rendimiento es deficiente no sólo en los datos de entrenamiento, sino también en los nuevos datos no vistos (datos de prueba). Sin embargo, estos modelos suelen tener una varianza baja, lo que significa que sus predicciones no cambian mucho si los entrenas con distintos subconjuntos de datos. La simplicidad los hace coherentes, aunque sistemáticamente erróneos.

Matemáticamente, esto se relaciona con la descomposición sesgo-varianza del error esperado del modelo. El error esperado de un modelo puede descomponerse en tres componentes: sesgo al cuadrado, varianza y error irreducible:

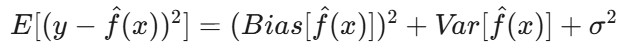
Dónde:

• E[(y - f̂(x))²] es el error cuadrático esperado de la predicción.

• Bias(f̂(x)) mide el error introducido al aproximar la función real f(x) con el modelo.

• Var(f̂(x)) es la variabilidad de la predicción del modelo para diferentes conjuntos de datos de entrenamiento.

• σ² representa el error irreducible: el ruido inherente a los datos que no se puede predecir.

En el ajuste insuficiente, el términoBias(f̂(x)) domina el error. El modelo es demasiado simple, lo que da lugar a errores sistemáticos y a que no capte la verdadera relación de los datos.

Contraste entre infraadaptación y sobreadaptación

Comprender la inadaptación resulta más claro si se compara con la sobreadaptación. Mientras que los modelos infraadaptados son demasiado simples, los modelos sobreadaptados son demasiado complejos. Aprenden los datos de entrenamiento demasiado bien, captando no sólo los patrones subyacentes, sino también el ruido y las fluctuaciones aleatorias.

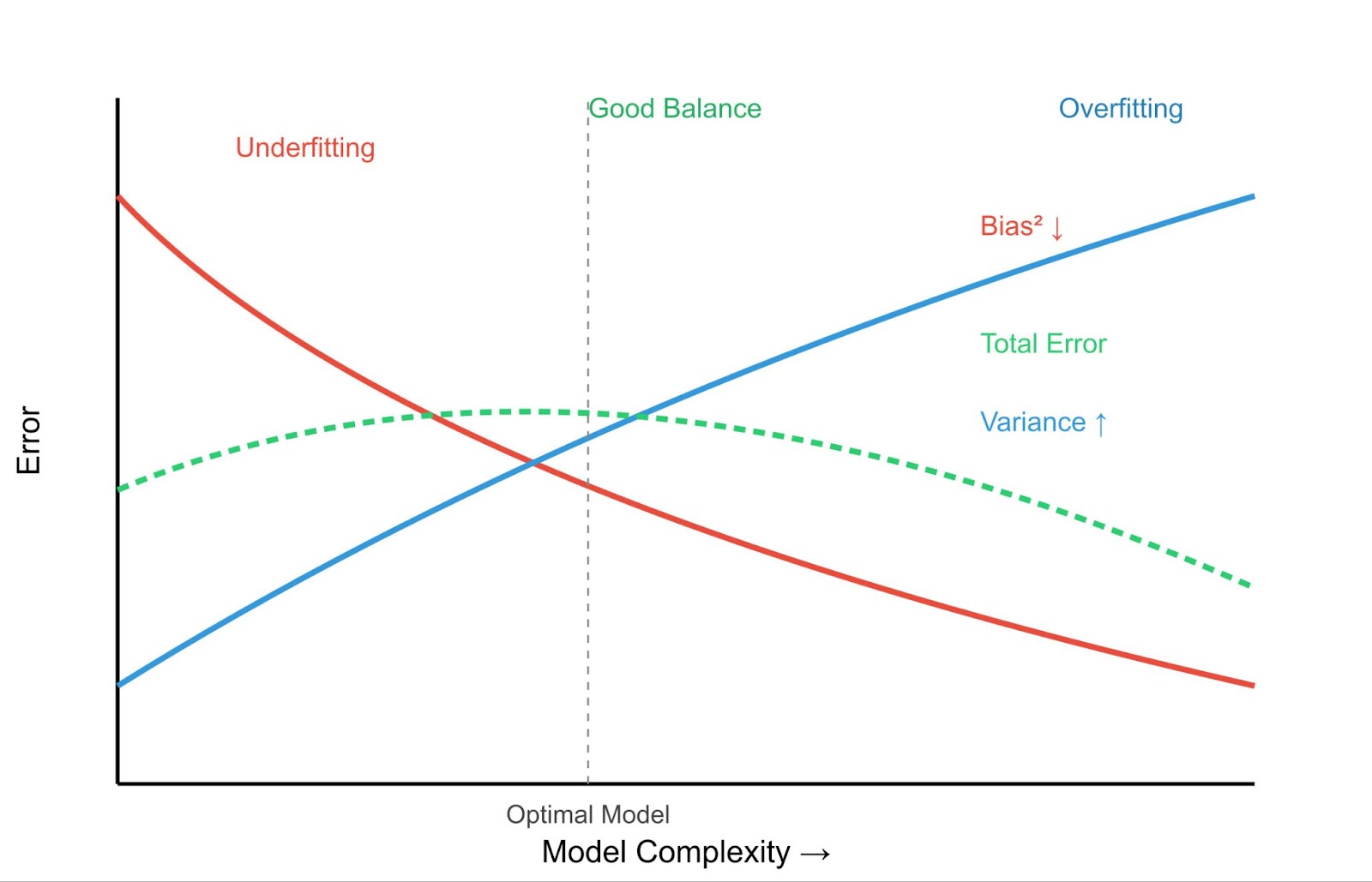
Bias Variance Trade-off - Imagen del autor

Veamos las principales diferencias entre infraadaptación y sobreadaptación:

Esto nos lleva al concepto crucial de la compensación sesgo-varianza.

• Sesgo elevado (ajuste insuficiente): Los modelos simples tienen un sesgo alto pero una varianza baja. Se equivocan sistemáticamente, pero no varían mucho con diferentes datos de entrenamiento.
• Varianza elevada (sobreajuste): Los modelos complejos tienen un sesgo bajo pero una varianza alta. Se ajustan muy bien a los datos de entrenamiento (bajo sesgo), pero son muy sensibles a los datos de entrenamiento específicos utilizados, lo que conduce a una mala generalización con nuevos datos. Puedes aprender más sobre esto en nuestro artículo ¿Qué es el sobreajuste?.

El objetivo es encontrar un punto óptimo: un modelo lo bastante complejo como para captar los patrones verdaderos (bajo sesgo), pero no tan complejo como para aprender el ruido (baja varianza).

Ejemplos:

• Ejemplo de ajuste insuficiente: Intentar predecir los precios de la vivienda, que dependen del tamaño, la ubicación, la antigüedad, etc., utilizando sólo el número de habitaciones. El modelo es demasiado simple (alto sesgo) y probablemente hará malas predicciones para la mayoría de las casas.
• Ejemplo de sobreajuste: Crear un modelo de regresión polinómica muy complejo que pase perfectamente por todos y cada uno de los puntos de datos de tu conjunto de entrenamiento del precio de la vivienda. Este modelo puede tener un error casi nulo en los datos de entrenamiento, pero tendrá un rendimiento terrible en las casas nuevas porque ha aprendido el ruido específico del conjunto de entrenamiento (alta varianza).

Comprender dónde se sitúa tu modelo en este espectro es importante para desarrollar soluciones eficaces de machine learning, como veremos en las siguientes secciones sobre cómo detectar y abordar la inadaptación.

Causas de la inadaptación e indicadores de diagnóstico

Ahora que entendemos qué es el infraajuste, veamos por qué ocurre y cómo puedes detectarlo en tus propios proyectos. Identificar la causa raíz es esencial para elegir la estrategia de mitigación adecuada. 

Causas principales de la inadaptación

Varios factores pueden dar lugar a un modelo de ajuste insuficiente:

Insuficiente complejidad del modelo

El algoritmo elegido puede ser demasiado simple para la estructura subyacente de los datos. Por ejemplo, utilizar un modelo de regresión lineal cuando la relación entre las características y la variable objetivo es muy poco lineal. El modelo carece intrínsecamente de capacidad para captar las complejidades.

Formación inadecuada

Puede que el modelo no se haya entrenado durante el tiempo suficiente (por ejemplo, muy pocas épocas en las redes neuronales) o con los parámetros de aprendizaje adecuados. Si el proceso de entrenamiento se detiene prematuramente, el modelo no habrá tenido suficientes oportunidades de aprender los patrones, aunque tenga capacidad para ello.

Mala representación de rasgos 

Las características utilizadas para entrenar el modelo podrían no representar adecuadamente los factores subyacentes que influyen en la variable objetivo. Esto puede significar:

• Faltan funciones importantes: Los predictores clave no se incluyeron en el conjunto de datos.
• Características irrelevantes: El conjunto de datos contiene ruido o características que no se correlacionan con el resultado, lo que puede inducir a error a un modelo simple.
• Características que necesitan transformación: Las características pueden requerir escalado, normalización o codificación (p. ej., variables categóricas) para ser útiles para el modelo.

Regularización excesiva

Las técnicas de regularización (como las penalizaciones L1 o L2) se utilizan principalmente para evitar el sobreajuste, añadiendo una penalización por complejidad. Sin embargo, si la intensidad de la regularización (por ejemplo, el parámetro lambda) se fija demasiado alta, puede penalizar excesivamente el modelo, obligándolo a simplificarse demasiado y provocando así un ajuste insuficiente. Más información sobre la regularización en Hacia la prevención del sobreajuste en el machine learning: Regularización.

Datos de baja calidad o insuficientes

• No hay datos suficientes: Si el conjunto de datos de entrenamiento es demasiado pequeño, puede que el modelo no tenga suficientes ejemplos para aprender eficazmente los patrones subyacentes.
• Ruido elevado: Si los datos son muy ruidosos, el modelo puede tener dificultades para distinguir la señal del ruido, sobre todo si se trata de un modelo simple.
• Valores perdidos: Una cantidad importante de datos perdidos puede dificultar la capacidad de aprendizaje del modelo, sobre todo si no se manejan adecuadamente. En Manejo de datos perdidos con imputaciones en R.

Métodos de detección

¿Cómo puedes saber si tu modelo está infraajustado? He aquí algunas técnicas habituales de diagnóstico:

Analizar las métricas de rendimiento 

El indicador más directo es el bajo rendimiento tanto en el conjunto de entrenamiento como en el conjunto de validación/prueba. Si tu modelo obtiene un error elevado (o una precisión baja, un R-cuadrado bajo, etc.) en los datos con los que se entrenó, es una señal clara de que no ha aprendido los patrones de forma eficaz. A diferencia de la sobreadaptación, en la que el rendimiento en el entrenamiento es excelente, pero el rendimiento en las pruebas es deficiente, la inadaptación muestra un rendimiento deficiente en todos los ámbitos.

Curvas de aprendizaje

Graficando el rendimiento del modelo (por ejemplo, el error o la precisión) en los conjuntos de entrenamiento y validación en función del tiempo de entrenamiento o del tamaño del conjunto de datos, puede ser muy esclarecedor. Para un modelo inadaptado, las curvas de aprendizaje suelen mostrar:

• Alto error de entrenamiento que se estanca pronto.
• Error de validación elevado que se aproxima al error de entrenamiento y también se estabiliza.
• Ambas curvas convergen en un nivel de error elevado, lo que indica que el modelo no mejora significativamente ni siquiera con más datos o entrenamiento.

Análisis de características

Revisa las funciones utilizadas. ¿Son relevantes? ¿Hay interacciones que no hayas captado? ¿Están escalados los rasgos numéricos? ¿Se codifican adecuadamente los rasgos categóricos? 

A veces, revisar la ingeniería de características puede revelar por qué el modelo tiene problemas. Los conceptos básicos se tratan en Fundamentos del machine learning en R. Para profundizar en las relaciones estadísticas, considera recursos como Inferencia estadística en R.

Modelización comparativa

Entrena un modelo más complejo (por ejemplo, un árbol de decisión o una máquina de refuerzo de gradiente si inicialmente utilizaste la regresión lineal) con los mismos datos. Si el modelo más complejo supera significativamente a tu modelo inicial tanto en el conjunto de entrenamiento como en el de validación, sugiere que tu modelo original probablemente no se ajustaba bien debido a una complejidad insuficiente. 

Puedes hacer un seguimiento de estas comparaciones utilizando las herramientas que se comentan en Experimentación de machine learning: Una introducción a los pesos y sesgos.

Si comprendes estas causas y los métodos de detección, podrás diagnosticar eficazmente un modelo de ajuste insuficiente y tomar medidas para mejorar su rendimiento.

Estrategias y buenas prácticas para mitigar la inadaptación

Una vez que has identificado la inadaptación, el siguiente paso es saber cómo solucionarla. Afortunadamente, varias estrategias eficaces pueden ayudar a aumentar la capacidad de tu modelo para aprender los patrones subyacentes en los datos. Veamos algunas de ellas:

Aumentar la complejidad del modelo

Si tu modelo es demasiado simple (sesgo alto), hacerlo más complejo puede resolver a menudo el desajuste. Podemos hacerlo de las siguientes maneras:

Selección del algoritmo

Cambia a un modelo más potente. Si la regresión lineal no se ajusta bien, prueba con la regresión polinómica, los árboles de decisión, los bosques aleatorios, las máquinas de refuerzo de gradiente (como XGBoost o LightGBM), o máquinas de vectores soporte (SVM) con núcleos no lineales. Estos modelos tienen intrínsecamente más capacidad para captar relaciones complejas.

Expansión polinómica de rasgos

Para los problemas de regresión, puedes crear características polinómicas a partir de las características numéricas existentes. Esto permite que los modelos lineales se ajusten a relaciones más complejas y curvas. Por ejemplo, si tienes una característica x, puedes añadir x2, x3, etc., como nuevas características. Scikit-learn proporciona PolynomialFeatures para ello.

Ajuste de hiperparámetros

Muchos modelos complejos tienen hiperparámetros que controlan su complejidad (por ejemplo, la profundidad de un árbol de decisión, el número de neuronas en la capa de una red neuronal, el parámetro C en las SVM). Ajustar estos hiperparámetros para permitir una mayor complejidad puede reducir el sesgo. 

Técnicas como la búsqueda en parrilla o la búsqueda aleatoria son esenciales en este caso. Aprende más con cursos como Ajuste de hiperparámetros en Python o Ajuste de hiperparámetros en R. Consulta también nuestro tutorial sobre Optimización de hiperparámetros en modelos de machine learning.

Ingeniería de rasgos y aumento de datos

A veces, el modelo no es el problema, sino la representación de los datos. Mejorar las características puede ayudar significativamente. Podemos hacerlo de las siguientes maneras:

Creación de características específicas de dominio

Utiliza tu conocimiento del dominio del problema para crear nuevas funciones que puedan ser más informativas. Por ejemplo, para predecir el precio de la vivienda, combinando el "número de dormitorios" y el "número de cuartos de baño" en una función de "total de habitaciones", o calculando la "antigüedad de la casa" a partir del "año de construcción".

Funciones de interacción

Crea rasgos que representen la interacción entre rasgos existentes (por ejemplo, multiplicando dos rasgos juntos). Esto puede ayudar a los modelos a captar los efectos sinérgicos.

Enriquecimiento de datos

Si es posible, aumenta tu conjunto de datos con fuentes de datos externas. Por ejemplo, añadiendo datos demográficos a la información de los clientes o datos meteorológicos a las predicciones de ventas.

Aumento de datos (principalmente para datos no estructurados)

En el caso de los datos de imágenes o texto, técnicas como girar o voltear las imágenes o utilizar la sustitución de sinónimos en el texto pueden aumentar artificialmente el tamaño y la diversidad del conjunto de entrenamiento, ayudando potencialmente al modelo a aprender patrones más robustos.

Ajuste de regularización

Si la causa del ajuste insuficiente es una regularizaciónexcesiva de, destinada a evitar el ajuste excesivo, tienes que reducirla. Reduce el valor del parámetro de regularización (por ejemplo, alfa en Ridge/Lasso, C en SVM - ten en cuenta que para las SVM, un C más pequeño significa una regularización más fuerte, por lo que aumentarías C).

Si utilizas el abandono, reduce la tasa de abandono (la fracción de neuronas abandonadas durante el entrenamiento). Una tarifa más baja retiene más capacidad de la red.

Encontrar el equilibrio adecuado suele requerir un ajuste cuidadoso, lo que pone de manifiesto una vez más la importancia de la optimización de los hiperparámetros.

Métodos de conjunto

Los métodos de conjunto combinan predicciones de varios modelos individuales (aprendices débiles) para producir una predicción final más sólida y robusta. Suelen ser muy eficaces para reducir tanto el sesgo como la varianza. Algunos de los métodos de conjunto son los siguientes:

• Bagging (por ejemplo, Random Forests): Entrena múltiples modelos (por ejemplo, árboles de decisión) de forma independiente en diferentes muestras bootstrap de los datos y promedia sus predicciones. Esto reduce principalmente la varianza, pero también puede ayudar si los aprendices de base están ligeramente sesgados. Consulta nuestro Tutorial de embolsado para más información.
• Boosting (por ejemplo, AdaBoost, Gradient Boosting): Entrena los modelos secuencialmente, y cada nuevo modelo se centra en corregir los errores cometidos por los anteriores. El refuerzo es especialmente eficaz para reducir el sesgo y convertir los aprendices débiles en fuertes, lo que lo convierte en una poderosa herramienta contra el ajuste insuficiente. Tenemos un . Guía de refuerzo para saber más.
• Apilando: Entrena varios tipos diferentes de modelos y luego utiliza otro modelo (un metaaprendizaje) para aprender a combinar mejor sus predicciones.

Aplicando estas estrategias, a menudo combinadas, puedes abordar eficazmente el ajuste insuficiente y construir modelos que capten mejor las complejidades de tus datos.

Aplicaciones prácticas y casos prácticos

Ver el ajuste insuficiente en acción con conjuntos de datos y código puede aclarar significativamente el concepto. Veamos ejemplos prácticos para demostrar cómo se comporta un modelo inadaptado y cómo se puede mejorar su rendimiento.

Ejemplo de ajuste insuficiente de regresión lineal

Una situación habitual de ajuste insuficiente se produce cuando se utiliza un modelo lineal simple para describir una relación no lineal. Ilustremos esto intentando ajustar un modelo de regresión lineal a unos datos que siguen un patrón cuadrático.

Generaremos datos sintéticos en los que la variable objetivo y tenga una relación cuadrática con una característica X. En primer lugar, ajustaremos un modelo de regresión lineal simple. Observaremos su escaso rendimiento (elevado Error Cuadrático Medio - ECM) y visualizaremos cómo no consigue captar la curva de los datos. 

A continuación, ampliaremos las características añadiendo un término polinómico y ajustaremos un modelo de regresión polinómica. Esto demostrará cómo el aumento de la complejidad del modelo puede reducir el sesgo y mejorar significativamente la precisión del modelo.

Empecemos importando las bibliotecas necesarias de la siguiente manera:

# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_error

Generemos datos sintéticos no lineales . Crearemos datos con una relación cuadrática: y = 0,5*X^2 + X + 2 + ruido.

np.random.seed(42) # for reproducibility
num_samples = 100
X = np.sort(10 * np.random.rand(num_samples, 1) - 5, axis=0) # Feature X (sorted for plotting)
y_true = 0.5 * X**2 + X + 2 # True quadratic relationship
y = y_true + np.random.randn(num_samples, 1) * 5 # Add some noise to make it realistic

Ahora, ajustaremos un modelo de regresión lineal simple (Modelo de desajuste) como se muestra a continuación:

linear_model = LinearRegression()
linear_model.fit(X, y)
y_pred_linear = linear_model.predict(X)
mse_linear = mean_squared_error(y, y_pred_linear)

print(f"--- Simple Linear Regression (Potential Underfitting Model) ---")
print(f"Mean Squared Error (MSE): {mse_linear:.2f}")
print(f"Model Coefficients (slope): {linear_model.coef_[0][0]:.2f}")
print(f"Model Intercept: {linear_model.intercept_[0]:.2f}")

Salida:

--- Simple Linear Regression (Potential Underfitting Model) ---

Mean Squared Error (MSE): 34.03

Model Coefficients (slope): 1.00

Model Intercept: 6.42

Ahora, ajustaremos un modelo de regresión polinómica (Modelo mejorado). Para ello, creamos características polinómicas (grado 2) y luego ajustamos un modelo lineal a estas características. El paso PolynomialFeatures añade nuevas funciones. El paso LinearRegression tiene coeficientes para cada uno.

Para el grado 2, esperamos coeficientes para X y X^2. Una canalización hace que este proceso sea más limpio. El atributo named_steps de la canalización permite acceder a pasos individuales, como se muestra a continuación:

polynomial_model = make_pipeline(PolynomialFeatures(degree=2, include_bias=False), LinearRegression())
polynomial_model.fit(X, y)
y_pred_poly = polynomial_model.predict(X)
mse_poly = mean_squared_error(y, y_pred_poly)

print(f"\n--- Polynomial Regression (Degree 2) ---")
print(f"Mean Squared Error (MSE): {mse_poly:.2f}")
poly_reg_coeffs = polynomial_model.named_steps['linearregression'].coef_[0]
poly_reg_intercept = polynomial_model.named_steps['linearregression'].intercept_[0]
print(f"Model Coefficients (for X, X^2): {poly_reg_coeffs[0]:.2f}, {poly_reg_coeffs[1]:.2f}")
print(f"Model Intercept: {poly_reg_intercept:.2f}")

Salida:

--- Polynomial Regression (Degree 2) ---

Mean Squared Error (MSE): 20.48

Model Coefficients (for X, X^2): 1.13, 0.50

Model Intercept: 2.04

Ahora vamos a visualizar el ajuste del modelo como se muestra a continuación:

# Visualization
plt.figure(figsize=(10, 4))
plt.scatter(X, y, s=30, label="Actual Data Points", alpha=0.7, edgecolors='k')
plt.plot(X, y_pred_linear, color='red', linewidth=2, label=f'Linear Fit (Underfitting)\nMSE: {mse_linear:.2f}')
plt.plot(X, y_pred_poly, color='green', linewidth=2, label=f'Polynomial Fit (Degree 2)\nMSE: {mse_poly:.2f}')
plt.title('Demonstrating Underfitting with Linear vs. Polynomial Regression', fontsize=16)
plt.xlabel('Feature X', fontsize=14)
plt.ylabel('Target y', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()

Salida:

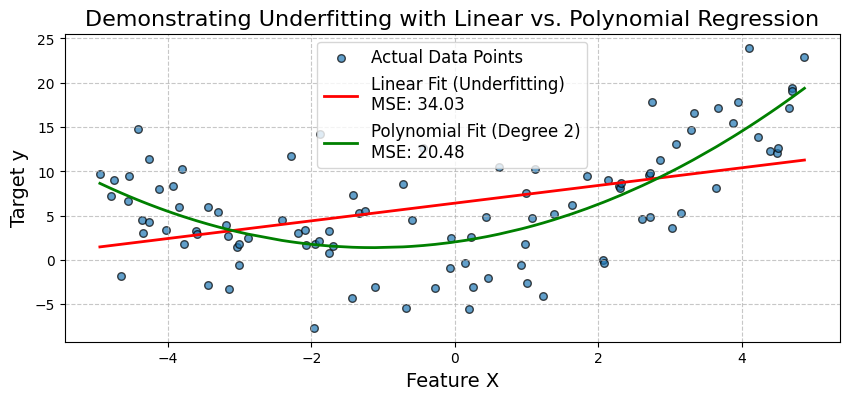
El gráfico confirma visualmente la falta de ajuste del modelo lineal simple. No capta la curva de los datos. El modelo de regresión polinómica, al incorporar el término X^2, proporciona un ajuste mucho mejor, como demuestra su menor MSE.

Esto demuestra que ampliar las características (aumentar la complejidad del modelo) puede reducir el sesgo y mejorar la precisión cuando la relación subyacente no es lineal. A continuación, veamos un caso práctico de diagnóstico médico.

Caso práctico de diagnóstico médico

Vamos a simular un escenario de diagnóstico médico utilizando el conocido conjunto de datos Cáncer de Mama Wisconsin (Diagnóstico) disponible en scikit-learn.

Primero intentaremos construir un modelo de clasificación utilizando sólo un subconjunto muy limitado de características, lo que podría llevar a un ajuste insuficiente. Después, utilizaremos un conjunto más amplio de características y, potencialmente, un algoritmo más complejo para demostrar la mejora.

Empecemos importando las bibliotecas necesarias de la siguiente manera:

# Import necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, roc_auc_score, confusion_matrix, ConfusionMatrixDisplay

Ahora, vamos a cargar y preparar los datos:

cancer = load_breast_cancer()
X = pd.DataFrame(cancer.data, columns=cancer.feature_names)
y = cancer.target # 0 for malignant, 1 for benign

A modo de demostración, seleccionemos un subconjunto muy limitado de características para el escenario de ajuste insuficiente. Puede que por sí solas no sean las más predictivas:

features_limited = ['mean texture', 'mean symmetry']
X_limited = X[features_limited]

Para el modelo mejorado, utilizaremos un subconjunto mayor (o todas las características). Seleccionemos las 10 primeras características para tener un conjunto más completo:

features_comprehensive = cancer.feature_names[:10]
X_comprehensive = X[features_comprehensive]

Dividamos los datos. Lo haremos por separado para cada conjunto de características, para mayor claridad:

X_train_lim, X_test_lim, y_train, y_test = train_test_split(X_limited, y, test_size=0.3, random_state=42, stratify=y)
X_train_comp, X_test_comp, _, _ = train_test_split(X_comprehensive, y, test_size=0.3, random_state=42, stratify=y) # y_train and y_test are the same

Escalemos las características, ya que esto es importante para la regresión logística y muchos otros algoritmos:

scaler_lim = StandardScaler().fit(X_train_lim)
X_train_lim_scaled = scaler_lim.transform(X_train_lim)
X_test_lim_scaled = scaler_lim.transform(X_test_lim)

scaler_comp = StandardScaler().fit(X_train_comp)
X_train_comp_scaled = scaler_comp.transform(X_train_comp)
X_test_comp_scaled = scaler_comp.transform(X_test_comp)

Ahora, vamos a ajustar una regresión logística con características limitadas:

print("Scenario 1: Logistic Regression (Limited Features - Potential Underfitting)")
log_reg_limited = LogisticRegression(random_state=42, solver='liblinear') # liblinear is good for small datasets
log_reg_limited.fit(X_train_lim_scaled, y_train)
y_pred_lim = log_reg_limited.predict(X_test_lim_scaled)
y_proba_lim = log_reg_limited.predict_proba(X_test_lim_scaled)[:, 1]

acc_lim = accuracy_score(y_test, y_pred_lim)
auc_lim = roc_auc_score(y_test, y_proba_lim)
print(f"Features used: {features_limited}")
print(f"Accuracy: {acc_lim:.4f}")
print(f"AUC: {auc_lim:.4f}")

Salida:

Scenario 1: Logistic Regression (Limited Features - Potential Underfitting)

Features used: ['mean texture', 'mean symmetry']

Accuracy: 0.7544

AUC: 0.8151

Adoptemos una estrategia de mitigación. Ajustaremos un modelo de regresión logística con más características:

print("Scenario 2: Logistic Regression (Comprehensive Features)")
log_reg_comp = LogisticRegression(random_state=42, solver='liblinear')
log_reg_comp.fit(X_train_comp_scaled, y_train)
y_pred_comp_lr = log_reg_comp.predict(X_test_comp_scaled)
y_proba_comp_lr = log_reg_comp.predict_proba(X_test_comp_scaled)[:, 1]

acc_comp_lr = accuracy_score(y_test, y_pred_comp_lr)
auc_comp_lr = roc_auc_score(y_test, y_proba_comp_lr)
print(f"Features used: First 10 features") # For brevity
print(f"Accuracy: {acc_comp_lr:.4f}")
print(f"AUC: {auc_comp_lr:.4f}")

Salida:

Scenario 2: Logistic Regression (Comprehensive Features)

Features used: First 10 features

Accuracy: 0.9181

AUC: 0.9831

Ahora, vamos a ajustar un modelo más complejo como el Random Forest con más características:

print("Scenario 3: Random Forest (Comprehensive Features)")
rf_comp = RandomForestClassifier(random_state=42, n_estimators=100) # n_estimators is a key hyperparameter
rf_comp.fit(X_train_comp_scaled, y_train) # RF can also benefit from scaled data, though less sensitive
y_pred_comp_rf = rf_comp.predict(X_test_comp_scaled)
y_proba_comp_rf = rf_comp.predict_proba(X_test_comp_scaled)[:, 1]

acc_comp_rf = accuracy_score(y_test, y_pred_comp_rf)
auc_comp_rf = roc_auc_score(y_test, y_proba_comp_rf)
print(f"Features used: First 10 features")
print(f"Accuracy: {acc_comp_rf:.4f}")
print(f"AUC: {auc_comp_rf:.4f}")

Salida:

Scenario 3: Random Forest (Comprehensive Features)

Features used: First 10 features

Accuracy: 0.9415

AUC: 0.9878

Vamos a gráficar y comparar la matriz de confusión de cada caso:

fig, axes = plt.subplots(1, 3, figsize=(20, 5))
fig.suptitle('Comparison of Model Performance (Confusion Matrices on Test Set)', fontsize=16)

# Model 1: Logistic Regression (Limited Features)
cm_lim = confusion_matrix(y_test, y_pred_lim)
disp_lim = ConfusionMatrixDisplay(confusion_matrix=cm_lim, display_labels=cancer.target_names)
disp_lim.plot(ax=axes[0], cmap='Blues')
axes[0].set_title(f'LogReg (Limited Features)\nAcc: {acc_lim:.2f}, AUC: {auc_lim:.2f}')

# Model 2: Logistic Regression (Comprehensive Features)
cm_comp_lr = confusion_matrix(y_test, y_pred_comp_lr)
disp_comp_lr = ConfusionMatrixDisplay(confusion_matrix=cm_comp_lr, display_labels=cancer.target_names)
disp_comp_lr.plot(ax=axes[1], cmap='Greens')
axes[1].set_title(f'LogReg (Comprehensive Features)\nAcc: {acc_comp_lr:.2f}, AUC: {auc_comp_lr:.2f}')

# Model 3: Random Forest (Comprehensive Features)
cm_comp_rf = confusion_matrix(y_test, y_pred_comp_rf)
disp_comp_rf = ConfusionMatrixDisplay(confusion_matrix=cm_comp_rf, display_labels=cancer.target_names)
disp_comp_rf.plot(ax=axes[2], cmap='Oranges')
axes[2].set_title(f'Random Forest (Comprehensive Features)\nAcc: {acc_comp_rf:.2f}, AUC: {auc_comp_rf:.2f}')

plt.tight_layout(rect=[0, 0, 1, 0.96]) # Adjust layout to make space for suptitle
plt.show()

Salida:

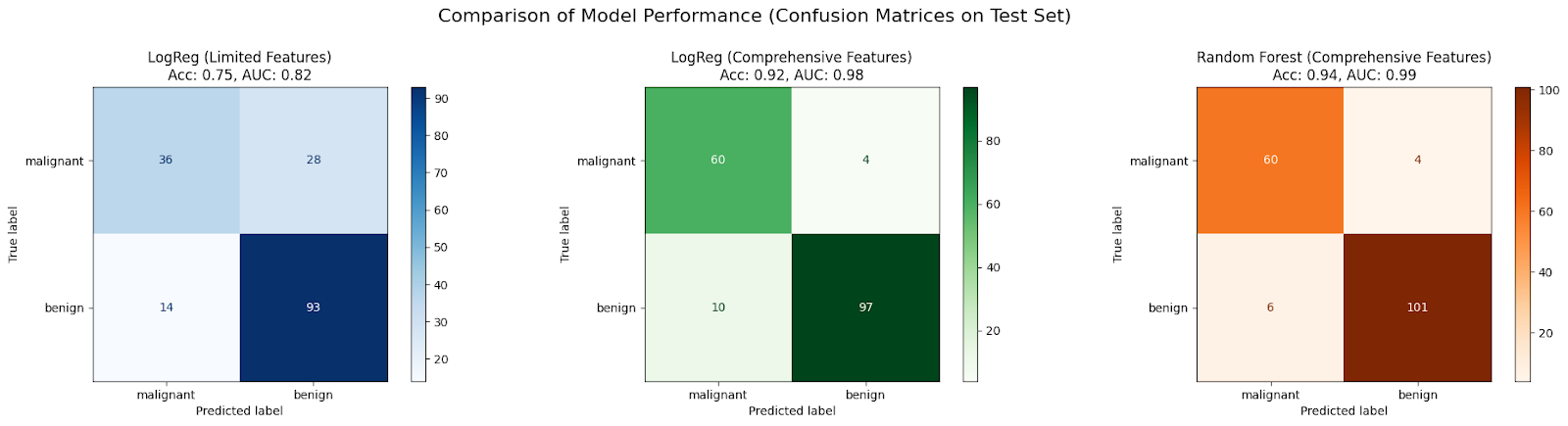
En este caso práctico, se espera que un modelo inicial LogisticRegression entrenado sólo con dos características (Escenario 1) no se ajuste lo suficiente debido a la insuficiencia de información, lo que daría lugar a una precisión y un AUC deficientes.

El rendimiento suele mejorar cuando el mismo algoritmo recibe un conjunto más amplio de características (Escenario 2), ya que tiene más datos de los que aprender, lo que reduce el sesgo.

A menudo se observa una mejora adicional utilizando un algoritmo más complejo como RandomForestClassifier con el conjunto completo de características (Escenario 3), porque puede captar las no linealidades y las interacciones de las características de forma más eficaz, reduciendo aún más el sesgo y mejorando el ajuste del modelo a los datos.

Temas avanzados y direcciones futuras

Aunque hemos tratado los fundamentos, el panorama del machine learning está en constante evolución. He aquí un breve vistazo a cómo la inadaptación se relaciona con áreas más avanzadas.

El papel del aprendizaje profundo

Los modelos de aprendizaje profundo, en particular las redes neuronales profundas con muchas capas, son conocidos por su gran capacidad, lo que significa que teóricamente pueden aproximar funciones muy complejas.

Debido a su complejidad inherente, los modelos de aprendizaje profundo suelen ser menos propensos a la inadaptación que los modelos más sencillos, siempre que se entrenen adecuadamente con datos suficientes. Su estructura les permite aprender automáticamente intrincadas representaciones de rasgos a partir de datos brutos (como píxeles en imágenes o palabras en texto).

Sin embargo, el aprendizaje profundo no es inmune a problemas que parecen como un ajuste insuficiente. Si una red está mal diseñada (por ejemplo, profundidad/anchura insuficientes para la tarea), no se entrena el tiempo suficiente o utiliza funciones de activación o algoritmos de optimización inadecuados, puede que siga sin converger y muestre un error de entrenamiento elevado.

Las innovaciones arquitectónicas como las conexiones residuales (ResNets) y las técnicas de normalización (Normalización por lotes) ayudan a entrenar redes muy profundas de forma eficaz, mitigando los problemas de gradiente evanescente/explosivo y permitiéndoles alcanzar su capacidad máxima, evitando así los problemas de convergencia que imitan el ajuste insuficiente.

Automatización del machine learning (AutoML)

Encontrar el modelo, las características y los hiperparámetros adecuados para evitar tanto el infraajuste como el sobreajuste puede llevar mucho tiempo. AutoML pretende automatizar este proceso.

Los marcos AutoML pueden explorar automáticamente distintos tipos de modelos (desde modelos lineales a conjuntos complejos y redes neuronales), realizar ingeniería y selección de características y optimizar hiperparámetros. Buscando sistemáticamente en un vasto espacio de posibilidades, AutoML puede identificar configuraciones de modelos que tengan la complejidad suficiente para evitar un ajuste insuficiente a los datos.

Métodos como la Búsqueda de Arquitectura Neuronal (NAS) diseñan automáticamente arquitecturas de red, mientras que sofisticadas técnicas de optimización de hiperparámetros (por ejemplo, la Optimización Bayesiana) encuentran eficazmente buenos ajustes de hiperparámetros. Estas herramientas pueden acelerar considerablemente el proceso de encontrar un modelo que se ajuste bien, reduciendo el esfuerzo manual necesario para diagnosticar y corregir un modelo que no se ajuste bien.

Conclusión

Comprender el dilema entre ajuste insuficiente y ajuste excesivo es fundamental para el éxito del machine learning. Hemos visto que la inadaptación surge cuando un modelo es demasiado simple (sesgo alto) para captar las tendencias subyacentes en los datos, lo que conduce a un rendimiento deficiente tanto en los datos de entrenamiento como en los no vistos. Las causas principales son la complejidad insuficiente del modelo, las características deficientes, el entrenamiento inadecuado y la regularización excesiva.

Diagnosticar la inadaptación implica examinar las métricas de rendimiento, gráficando curvas de aprendizaje y comparando modelos, a menudo con la ayuda de código. Afortunadamente, disponemos de varias estrategias para corregir la inadaptación: aumentar la complejidad del modelo (elegir mejores algoritmos, expansión de características, ajuste de hiperparámetros), mejorar las características (ingeniería de características, enriquecimiento de datos), ajustar la regularización y emplear potentes métodos de conjunto, como se demuestra en nuestros ejemplos de código.

Para aprender estas técnicas y otras más con ejemplos prácticos, consulta nuestro curso Programa de Fundamentos de Machine Learning en Python.