Was ist Underfitting? Wie man hohe Verzerrungen in ML-Modellen erkennt und überwindet

Bei der Erstellung von Modellen zur Vorhersage von Ergebnissen oder zur Aufdeckung von Mustern werden wir auf verschiedene Herausforderungen stoßen. Eine häufige Hürde ist die Erstellung eines Modells, das die zugrunde liegenden Trends in deinen Daten genau erfasst. Manchmal sind die Modelle zu einfach und lernen die komplexen Zusammenhänge nicht, was zu einer schlechten Leistung führt. Dieses Phänomen wird als Underfitting bezeichnet.

Ein unzureichend angepasstes Modell schneidet nicht nur bei den Daten schlecht ab, auf denen es trainiert wurde, sondern kann auch nicht auf neue, ungesehene Daten verallgemeinert werden. Das bedeutet, dass deine Vorhersagen in der realen Welt unzuverlässig sein könnten. Das Erkennen und Beheben von Unteranpassungen ist ein wichtiger Schritt, um robuste und effektive Modelle für maschinelles Lernen zu entwickeln. 

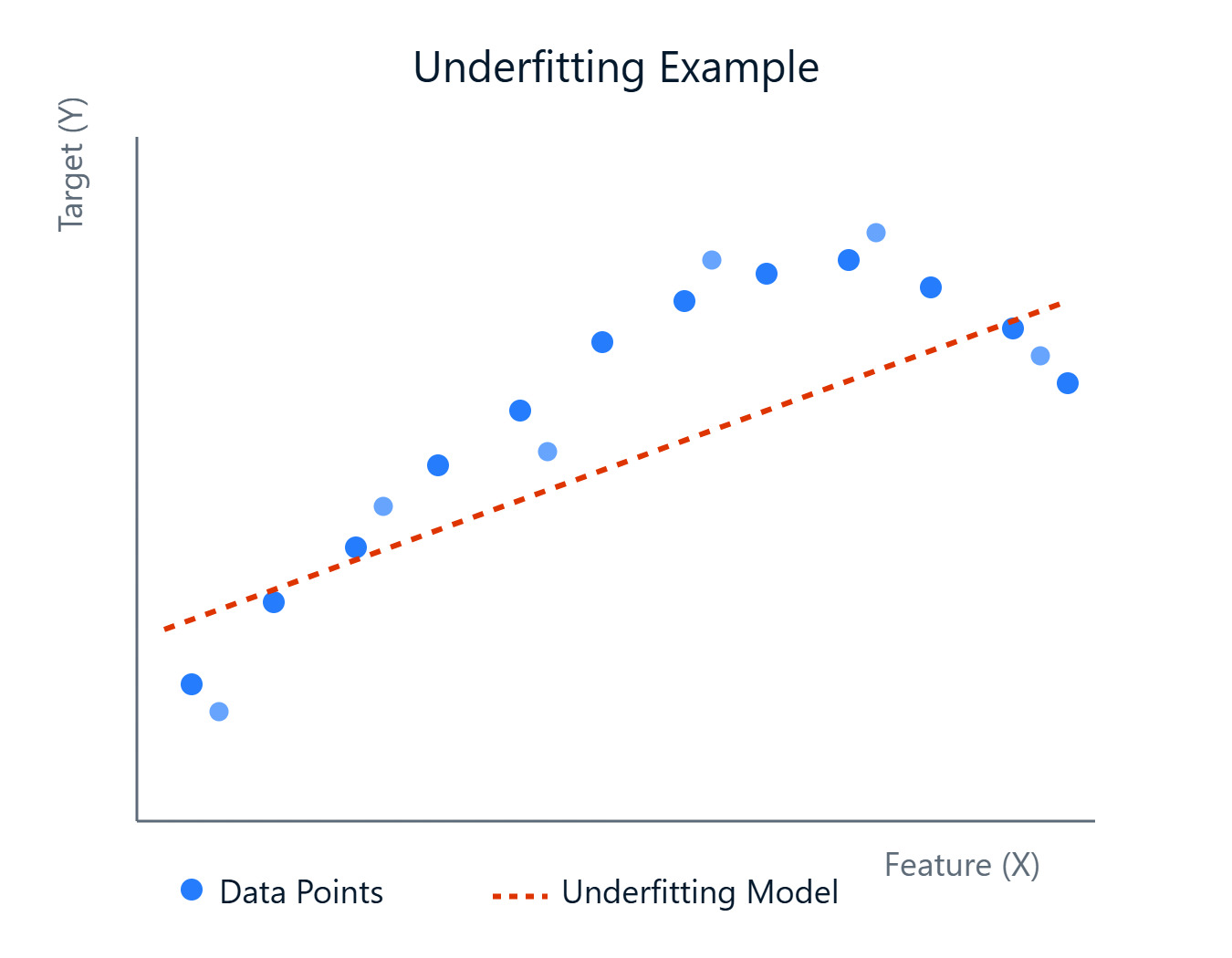
Bild vom Autor

In diesem Artikel schauen wir uns an, was Underfitting ist, warum es passiert, wie man es erkennt und vor allem, wie man es beheben kann. Wenn du dich praktisch mit maschinellem Lernen beschäftigen möchtest, solltest du dir unseren Grundlagen des maschinellen Lernens in Python.

Was ist Underfitting?

Schauen wir uns das Konzept der Unteranpassung genauer an und wie es sich von seinem Gegenstück, der Überanpassung, unterscheidet. Das Verständnis dieser Unterscheidung ist grundlegend für die Modelldiagnose und -verbesserung.

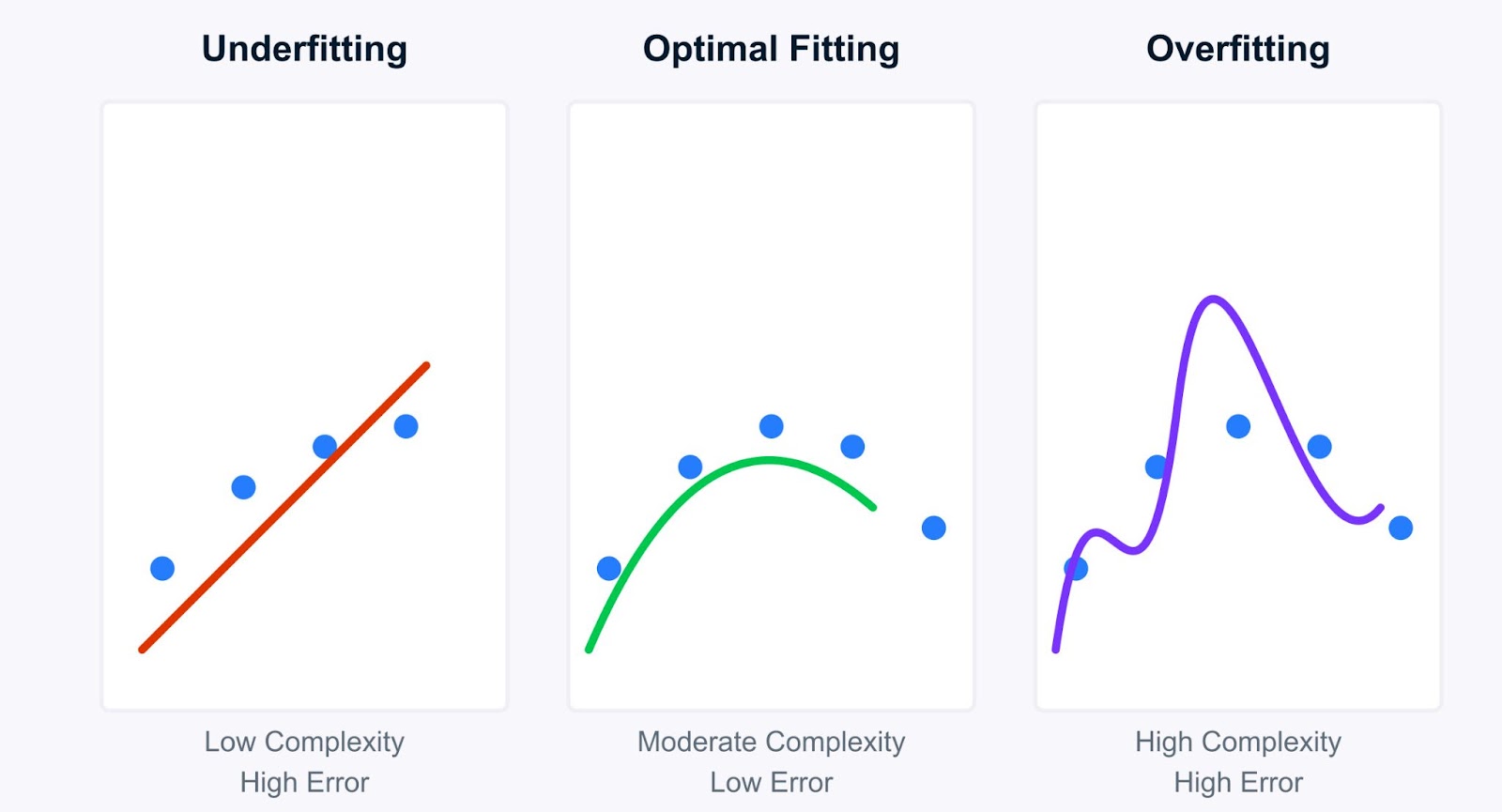
Bild vom Autor

Einfach ausgedrückt: Underfitting liegt vor, wenn ein maschinelles Lernmodell zu einfach ist, um die zugrunde liegenden Muster in den Trainingsdaten zu erfassen. Stell dir vor, du versuchst, eine gerade Linie durch Datenpunkte zu ziehen, die eindeutig einer Kurve folgen, und die Linie (unser Modell) ist einfach nicht komplex genug. Ein unzureichend angepasstes Modell leidet unter einer starken Verzerrung, d. h. es macht starke Annahmen über die Daten (z. B. nimmt es eine lineare Beziehung an, obwohl es keine gibt). 

Weil er die Daten nicht gut lernt, schneidet er nicht nur bei den Trainingsdaten schlecht ab, sondern auch bei neuen, ungesehenen Daten (Testdaten). Diese Modelle haben jedoch in der Regel eine geringe Varianz, d.h. ihre Vorhersagen ändern sich kaum, wenn du sie auf verschiedenen Teilmengen der Daten trainierst. Die Einfachheit macht sie konsequent, wenn auch konsequent falsch.

Mathematisch gesehen handelt es sich dabei um die Bias-Varianz-Zerlegung des erwarteten Fehlers des Modells. Der erwartete Fehler eines Modells lässt sich in drei Komponenten aufteilen: Bias zum Quadrat, Varianz und irreduzibler Fehler:

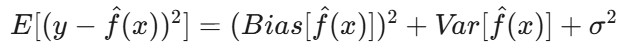
Wo:

• E[(y - f̂(x))²] ist der erwartete quadratische Fehler der Vorhersage.

• Bias(f̂(x)) misst den Fehler, der durch die Annäherung der realen Funktion f(x) mit dem Modell entsteht.

• Var(f̂(x)) ist die Variabilität der Modellvorhersage für verschiedene Trainingsdatensätze.

• σ² steht für den irreduziblen Fehler - das inhärente Rauschen in den Daten, das nicht vorhergesagt werden kann.

Bei einer Unteranpassung dominiert der TermBias(f̂(x)) den Fehler. Das Modell ist zu einfach, was zu systematischen Fehlern führt und die wahre Beziehung zwischen den Daten nicht erfasst.

Gegenüberstellung von Underfitting und Overfitting

Das Verständnis von Underfitting wird im Vergleich zu Overfitting klarer. Während Modelle mit zu geringer Passgenauigkeit zu einfach sind, sind Modelle mit zu hoher Passgenauigkeit zu komplex. Sie lernen die Trainingsdaten zu gut und erfassen nicht nur die zugrunde liegenden Muster, sondern auch das Rauschen und die zufälligen Schwankungen.

Bias Variance Trade-off - Bild vom Autor

Schauen wir uns die wichtigsten Unterschiede zwischen Underfitting und Overfitting an:

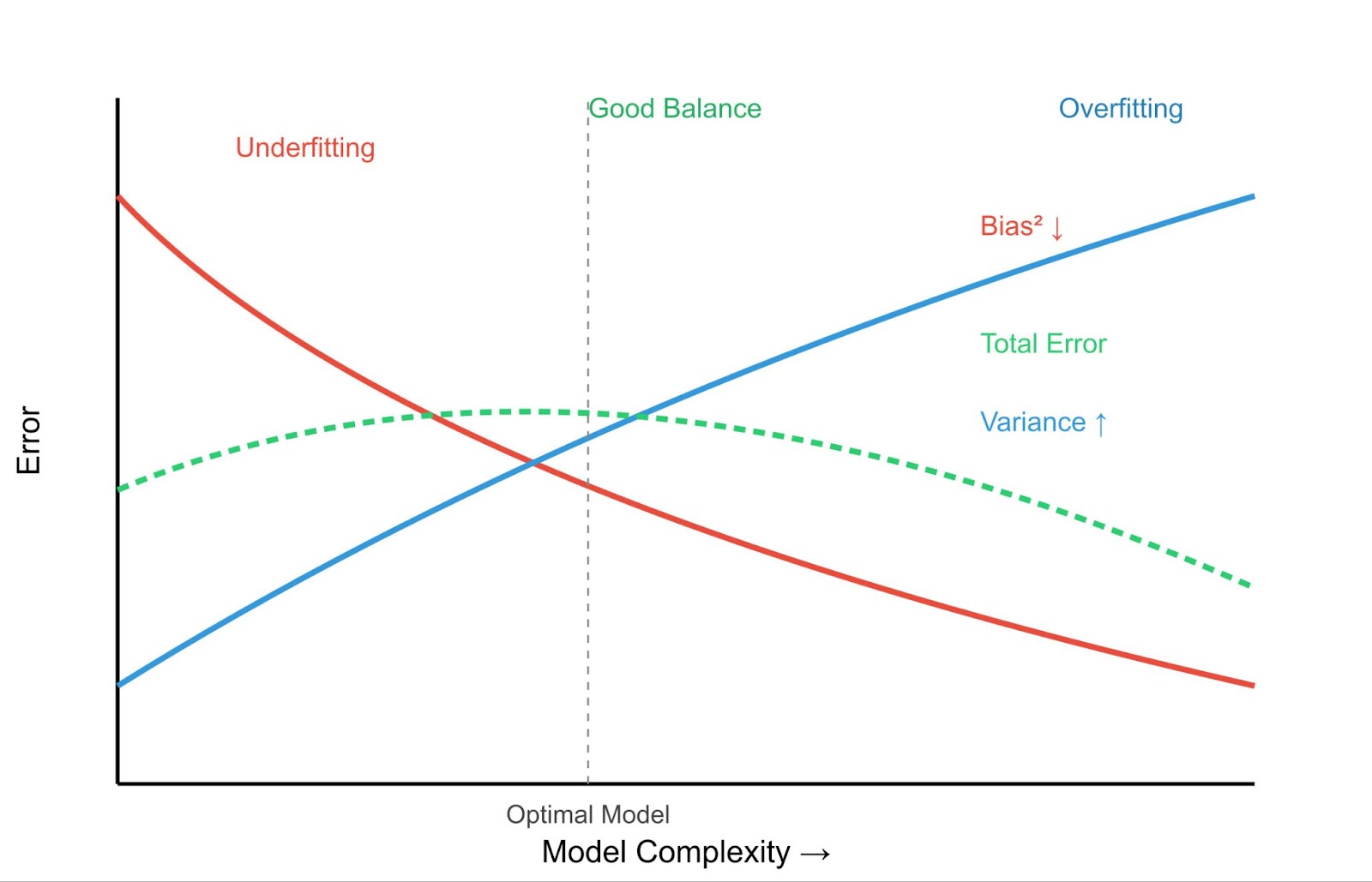
Dies führt zu dem entscheidenden Konzept des Bias-Variance-Tradeoffs.

• Hohe Verzerrung (Underfitting): Einfache Modelle haben eine hohe Verzerrung, aber eine geringe Varianz. Sie sind durchweg falsch, variieren aber bei unterschiedlichen Trainingsdaten nicht sehr.
• Hohe Varianz (Overfitting): Komplexe Modelle haben eine geringe Verzerrung, aber eine hohe Varianz. Sie passen sehr gut zu den Trainingsdaten (geringe Verzerrung), sind aber sehr empfindlich gegenüber den verwendeten Trainingsdaten, was zu einer schlechten Generalisierung auf neue Daten führt. Mehr dazu erfährst du in unserem Artikel Was ist Overfitting?.

Das Ziel ist es, einen Sweet Spot zu finden: ein Modell, das komplex genug ist, um die wahren Muster zu erfassen (geringe Verzerrung), aber nicht so komplex, dass es das Rauschen lernt (geringe Varianz).

Beispiele:

• Underfitting Beispiel: Der Versuch, Hauspreise, die von Größe, Lage, Alter usw. abhängen, nur anhand der Anzahl der Zimmer vorherzusagen. Das Modell ist zu einfach (hohe Verzerrung) und wird wahrscheinlich für die meisten Häuser schlechte Vorhersagen machen.
• Beispiel für Überanpassung: Erstellen eines hochkomplexen polynomialen Regressionsmodells, das jeden einzelnen Datenpunkt in deinem Hauspreis-Trainingssatz perfekt durchläuft. Dieses Modell kann bei den Trainingsdaten einen Fehler von fast Null haben, aber es wird bei neuen Häusern schlecht abschneiden, weil es das für die Trainingsdaten spezifische Rauschen (hohe Varianz) gelernt hat.

Zu wissen, wo dein Modell in diesem Spektrum liegt, ist wichtig für die Entwicklung effektiver maschineller Lernlösungen, wie wir in den folgenden Abschnitten über die Erkennung und Behebung von Unteranpassungen sehen werden.

Ursachen für Unterversorgung und diagnostische Indikatoren

Da wir nun wissen, was Underfitting ist, wollen wir sehen, warum es passiert und wie du es in deinen eigenen Projekten erkennen kannst. Die Ermittlung der Ursache ist entscheidend für die Wahl der richtigen Abhilfestrategie. 

Hauptursachen für unzureichende Anpassung

Mehrere Faktoren können dazu führen, dass ein Modell nicht richtig passt:

Unzureichende Modellkomplexität

Der gewählte Algorithmus könnte zu einfach für die zugrunde liegende Struktur der Daten sein. Zum Beispiel die Verwendung eines linearen Regressionsmodells, wenn die Beziehung zwischen den Merkmalen und der Zielvariable stark nicht-linear ist. Das Modell ist von Natur aus nicht in der Lage, die komplexen Zusammenhänge zu erfassen.

Unzureichende Ausbildung

Das Modell wurde vielleicht nicht lange genug trainiert (z. B. zu wenige Epochen in neuronalen Netzen) oder mit den richtigen Lernparametern. Wenn der Trainingsprozess vorzeitig abgebrochen wird, hatte das Modell nicht genügend Gelegenheit, die Muster zu lernen, auch wenn es die Fähigkeit dazu hat.

Schlechte Darstellung von Merkmalen 

Die Merkmale, die zum Trainieren des Modells verwendet werden, repräsentieren die zugrunde liegenden Faktoren, die die Zielvariable beeinflussen, möglicherweise nicht angemessen. Das könnte bedeuten:

• Es fehlen wichtige Funktionen: Wichtige Prädiktoren wurden nicht in den Datensatz aufgenommen.
• Unwichtige Merkmale: Der Datensatz enthält Rauschen oder Merkmale, die nicht mit dem Ergebnis korrelieren und ein einfaches Modell in die Irre führen können.
• Merkmale, die verändert werden müssen: Merkmale müssen möglicherweise skaliert, normalisiert oder kodiert werden (z. B. kategoriale Variablen), um für das Modell nützlich zu sein.

Exzessive Regularisierung

Regularisierungstechniken (wie L1- oder L2-Penalties) werden in erster Linie eingesetzt, um eine Überanpassung zu verhindern, indem ein Malus für die Komplexität hinzugefügt wird. Wenn die Stärke der Regularisierung (z. B. der Lambda-Parameter) jedoch zu hoch angesetzt wird, kann das Modell zu stark bestraft werden, so dass es zu einfach wird und zu wenig passt. Erfahre mehr über Regularisierung in Towards Preventing Overfitting in Machine Learning: Regularisierung.

Geringe Qualität oder unzureichende Daten

• Nicht genug Daten: Wenn der Trainingsdatensatz zu klein ist, hat das Modell möglicherweise nicht genug Beispiele, um die zugrunde liegenden Muster effektiv zu lernen.
• Hoher Lärm: Wenn die Daten sehr verrauscht sind, kann das Modell Schwierigkeiten haben, das Signal vom Rauschen zu unterscheiden, vor allem, wenn es sich um ein einfaches Modell handelt.
• Fehlende Werte: Große Mengen fehlender Daten können die Lernfähigkeit des Modells beeinträchtigen, insbesondere wenn sie nicht richtig behandelt werden. Techniken für den Umgang damit werden behandelt in Umgang mit fehlenden Daten mit Imputationen in R.

Erkennungsmethoden

Woran erkennst du, dass dein Modell nicht richtig angepasst ist? Hier sind einige gängige Diagnoseverfahren:

Analysieren von Leistungskennzahlen 

Der eindeutigste Indikator ist eine schlechte Leistung sowohlin der Trainingsmenge als auch in der Validierungs-/Testmenge. Wenn dein Modell bei den Daten, für die es trainiert wurde, einen hohen Fehler (oder eine niedrige Genauigkeit, ein niedriges R-Quadrat usw.) erzielt, ist das ein deutliches Zeichen dafür, dass es die Muster nicht effektiv gelernt hat. Im Gegensatz zur Überanpassung, bei der die Trainingsleistung hervorragend, die Testleistung aber schlecht ist, zeigt die Unteranpassung eine durchweg schlechte Leistung.

Lernkurven

Es kann sehr aufschlussreich sein, die Leistung des Modells (z. B. Fehler oder Genauigkeit) auf den Trainings- und Validierungssätzen in Abhängigkeit von der Trainingszeit oder der Größe des Datensatzes darzustellen. Bei einem unzureichend angepassten Modell zeigen die Lernkurven typischerweise:

• Hoher Trainingsfehler, der schon früh zum Stillstand kommt.
• Hoher Validierungsfehler, der nahe am Trainingsfehler liegt, und auch Plateaus.
• Beide Kurven konvergieren bei einem hohen Fehlerniveau, was bedeutet, dass sich das Modell auch mit mehr Daten oder Training nicht wesentlich verbessert.

Merkmal-Analyse

Überprüfe die verwendeten Funktionen. Sind sie relevant? Gibt es Interaktionen, die du nicht festgehalten hast? Sind numerische Merkmale skaliert? Sind kategoriale Merkmale angemessen kodiert? 

Manchmal kann ein erneuter Blick auf das Feature Engineering zeigen, warum das Modell Probleme hat. Grundlegende Konzepte werden behandelt in Grundlagen des maschinellen Lernens in R. Wenn du tiefere Einblicke in statistische Zusammenhänge gewinnen willst, solltest du dir Ressourcen wie Statistische Inferenz in R.

Vergleichende Modellierung

Trainiere ein komplexeres Modell (z. B. einen Entscheidungsbaum oder eine Gradient-Boosting-Maschine, wenn du ursprünglich eine lineare Regression verwendet hast) mit denselben Daten. Wenn das komplexere Modell dein ursprüngliches Modell sowohl in den Trainings- als auch in den Validierungssets deutlich übertrifft, deutet das darauf hin, dass dein ursprüngliches Modell aufgrund zu geringer Komplexität wahrscheinlich nicht richtig angepasst war. 

Du kannst solche Vergleiche mit den Tools nachverfolgen, die in Machine Learning Experimentation besprochen werden : Eine Einführung in Gewichte und Verzerrungen.

Wenn du diese Ursachen und Erkennungsmethoden verstehst, kannst du ein unzureichend angepasstes Modell effektiv diagnostizieren und Schritte unternehmen, um seine Leistung zu verbessern.

Strategien und bewährte Praktiken zur Eindämmung von Fehlanpassungen

Wenn du eine Unteranpassung festgestellt hast, geht es im nächsten Schritt darum, wie du sie beheben kannst. Zum Glück gibt es einige wirksame Strategien, die die Fähigkeit deines Modells, die zugrunde liegenden Muster in den Daten zu lernen, verbessern können. Schauen wir uns einige von ihnen an:

Erhöhung der Modellkomplexität

Wenn dein Modell zu einfach ist (hohe Verzerrung), kannst du es oft komplexer machen, um das Underfitting zu beheben. Wir können das auf folgende Weise tun:

Auswahl des Algorithmus

Wechsle zu einem leistungsstärkeren Modell. Wenn die lineare Regression nicht richtig passt, versuche es mit polynomialer Regression, Entscheidungsbäumen, Random Forests, Gradient-Boosting-Maschinen (wie XGBoost oder LightGBM) oder Support-Vektor-Maschinen (SVMs) mit nicht linearen Kerneln. Diese Modelle haben von Natur aus mehr Kapazität, um komplexe Beziehungen zu erfassen.

Polynomiale Merkmalserweiterung

Für Regressionsprobleme kannst du Polynom-Features aus deinen bestehenden numerischen Features erstellen. So können lineare Modelle komplexere, gekrümmte Beziehungen abbilden. Wenn du zum Beispiel ein Merkmal x hast, kannst du x2, x3, usw. als neue Merkmale hinzufügen. Scikit-learn bietet dafür PolynomialFeatures.

Hyperparameter-Abstimmung

Viele komplexe Modelle haben Hyperparameter, die ihre Komplexität steuern (z. B. die Tiefe eines Entscheidungsbaums, die Anzahl der Neuronen in einer Schicht eines neuronalen Netzes, der Parameter C in SVMs). Wenn du diese Hyperparameter so abstimmst, dass sie mehr Komplexität zulassen, kannst du Verzerrungen reduzieren. 

Techniken wie Grid Search oder Randomized Search sind hier unerlässlich. Lernen Sie mehr mit Kursen wie Hyperparameter-Tuning in Python oder Hyperparameter-Abstimmung in R. Siehe auch unser Tutorium über Hyperparameter-Optimierung in Machine Learning Modellen.

Feature Engineering und Datenerweiterung

Manchmal ist nicht das Modell das Problem, sondern die Darstellung der Daten. Die Verbesserung der Funktionen kann erheblich helfen. Das können wir auf folgende Weise tun:

Erstellung bereichsspezifischer Merkmale

Nutze dein Wissen über den Problembereich, um neue Funktionen zu entwickeln, die informativer sein könnten. Zum Beispiel bei der Vorhersage von Hauspreisen, indem du die "Anzahl der Schlafzimmer" und die "Anzahl der Badezimmer" zu einem Merkmal "Gesamtanzahl der Zimmer" kombinierst oder das "Hausalter" aus dem "Baujahr" berechnest.

Interaktionsmerkmale

Erstelle Merkmale, die die Interaktion zwischen bestehenden Merkmalen darstellen (z. B. die Multiplikation zweier Merkmale). Dies kann dazu beitragen, dass Modelle Synergieeffekte erfassen.

Datenanreicherung

Ergänze deinen Datensatz nach Möglichkeit mit externen Datenquellen. Zum Beispiel, indem du demografische Daten zu Kundeninformationen oder Wetterdaten zu Umsatzprognosen hinzufügst.

Datenerweiterung (hauptsächlich für unstrukturierte Daten)

Bei Bild- oder Textdaten können Techniken wie das Drehen/Spiegeln von Bildern oder das Ersetzen von Synonymen im Text die Größe und Vielfalt der Trainingsmenge künstlich erhöhen, was dem Modell helfen kann, robustere Muster zu lernen.

Anpassung der Regularisierung

Wenn die Unteranpassung durch eine übermäßige Regularisierung verursacht wird , die eine Überanpassung verhindern soll, musst du sie zurückdrehen. Verringere den Wert des Regularisierungsparameters (z. B. Alpha bei Ridge/Lasso, C bei SVMs - beachte, dass bei SVMs ein kleineres C eine stärkere Regularisierung bedeutet , du solltest also Cerhöhen ).

Wenn du Dropouts verwendest, reduziere die Dropout-Rate (den Anteil der Neuronen, die während des Trainings ausfallen). Eine niedrigere Rate hält mehr Netzkapazität bereit.

Um das richtige Gleichgewicht zu finden, ist oft eine sorgfältige Abstimmung erforderlich, was wiederum die Bedeutung der Optimierung der Hyperparameter unterstreicht.

Ensemble-Methoden

Ensemble-Methoden kombinieren Vorhersagen aus mehreren Einzelmodellen (schwache Lerner), um eine stärkere, robustere Endvorhersage zu erhalten. Sie sind oft sehr effektiv, um sowohl Verzerrungen als auch Varianz zu reduzieren. Einige der Ensemble-Methoden sind wie folgt:

• Bagging (z.B. Random Forests): Trainiert mehrere Modelle (z. B. Entscheidungsbäume) unabhängig voneinander auf verschiedenen Bootstrap-Stichproben der Daten und bildet den Durchschnitt ihrer Vorhersagen. Dies verringert in erster Linie die Varianz, kann aber auch helfen, wenn die Basislernenden leicht verzerrt sind. Schau dir unser Anleitung zum Absacken für weitere Informationen.
• Boosting (z.B. AdaBoost, Gradient Boosting): Die Modelle werden nacheinander trainiert, wobei sich jedes neue Modell darauf konzentriert, die Fehler der vorherigen Modelle zu korrigieren. Boosting ist besonders effektiv, wenn es darum geht, Verzerrungen zu reduzieren und schwache Lerner in starke Lerner zu verwandeln, was es zu einem mächtigen Werkzeug gegen Underfitting macht. Wir haben eine . Anleitung zum Boosten um mehr zu erklären.
• Stapeln: Trainiert mehrere verschiedene Arten von Modellen und verwendet dann ein anderes Modell (einen Meta-Learner), um zu lernen, wie man ihre Vorhersagen am besten kombiniert.

Wenn du diese Strategien - oft in Kombination - anwendest, kannst du das Underfitting wirksam bekämpfen und Modelle erstellen, die die Komplexität deiner Daten besser erfassen.

Praktische Anwendungen und Fallstudien

Wenn du Underfitting anhand von Datensätzen und Code in Aktion siehst, wird das Konzept deutlich. Schauen wir uns praktische Beispiele an, um zu zeigen, wie sich ein unzureichend angepasstes Modell verhält und wie seine Leistung verbessert werden kann.

Beispiel für die Unteranpassung der linearen Regression

Ein häufiges Szenario für Underfitting tritt auf, wenn ein einfaches lineares Modell verwendet wird, um eine nichtlineare Beziehung zu beschreiben. Veranschaulichen wir uns das, indem wir versuchen, ein lineares Regressionsmodell an Daten anzupassen, die einem quadratischen Muster folgen.

Wir werden synthetische Daten erzeugen, bei denen die Zielvariable y eine quadratische Beziehung zu einem Merkmal X hat . Zuerst passen wir ein einfaches lineares Regressionsmodell an. Wir werden seine schlechte Leistung (hoher mittlerer quadratischer Fehler - MSE) beobachten und sehen, wie er die Kurve der Daten nicht erfassen kann. 

Dann erweitern wir die Merkmale, indem wir einen polynomialen Term hinzufügen und ein polynomiales Regressionsmodell anpassen. Dies wird zeigen, wie die Erhöhung der Modellkomplexität die Verzerrungen reduzieren und die Genauigkeit des Modells deutlich verbessern kann.

Beginnen wir damit, die notwendigen Bibliotheken wie folgt zu importieren:

# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
from sklearn.metrics import mean_squared_error

Lass uns synthetische nicht-lineare Daten erzeugen. Wir werden Daten mit einer quadratischen Beziehung erstellen: y = 0,5*X^2 + X + 2 + Rauschen.

np.random.seed(42) # for reproducibility
num_samples = 100
X = np.sort(10 * np.random.rand(num_samples, 1) - 5, axis=0) # Feature X (sorted for plotting)
y_true = 0.5 * X**2 + X + 2 # True quadratic relationship
y = y_true + np.random.randn(num_samples, 1) * 5 # Add some noise to make it realistic

Jetzt passen wir ein einfaches lineares Regressionsmodell (Underfitting Model) an, wie unten gezeigt:

linear_model = LinearRegression()
linear_model.fit(X, y)
y_pred_linear = linear_model.predict(X)
mse_linear = mean_squared_error(y, y_pred_linear)

print(f"--- Simple Linear Regression (Potential Underfitting Model) ---")
print(f"Mean Squared Error (MSE): {mse_linear:.2f}")
print(f"Model Coefficients (slope): {linear_model.coef_[0][0]:.2f}")
print(f"Model Intercept: {linear_model.intercept_[0]:.2f}")

Ausgabe:

--- Simple Linear Regression (Potential Underfitting Model) ---

Mean Squared Error (MSE): 34.03

Model Coefficients (slope): 1.00

Model Intercept: 6.42

Jetzt passen wir ein polynomiales Regressionsmodell an (verbessertes Modell). Dazu erstellen wir polynomiale Merkmale (Grad 2) und passen dann ein lineares Modell an diese Merkmale an. Der Schritt PolynomialFeatures fügt neue Funktionen hinzu. Der Schritt LinearRegression hat Koeffizienten für jeden.

Für Grad 2 erwarten wir Koeffizienten für X und X^2. Eine Pipeline macht diesen Prozess sauberer. Das Attribut named_steps der Pipeline ermöglicht den Zugriff auf einzelne Schritte, wie unten dargestellt:

polynomial_model = make_pipeline(PolynomialFeatures(degree=2, include_bias=False), LinearRegression())
polynomial_model.fit(X, y)
y_pred_poly = polynomial_model.predict(X)
mse_poly = mean_squared_error(y, y_pred_poly)

print(f"\n--- Polynomial Regression (Degree 2) ---")
print(f"Mean Squared Error (MSE): {mse_poly:.2f}")
poly_reg_coeffs = polynomial_model.named_steps['linearregression'].coef_[0]
poly_reg_intercept = polynomial_model.named_steps['linearregression'].intercept_[0]
print(f"Model Coefficients (for X, X^2): {poly_reg_coeffs[0]:.2f}, {poly_reg_coeffs[1]:.2f}")
print(f"Model Intercept: {poly_reg_intercept:.2f}")

Ausgabe:

--- Polynomial Regression (Degree 2) ---

Mean Squared Error (MSE): 20.48

Model Coefficients (for X, X^2): 1.13, 0.50

Model Intercept: 2.04

Jetzt wollen wir die Modellanpassung wie unten dargestellt visualisieren:

# Visualization
plt.figure(figsize=(10, 4))
plt.scatter(X, y, s=30, label="Actual Data Points", alpha=0.7, edgecolors='k')
plt.plot(X, y_pred_linear, color='red', linewidth=2, label=f'Linear Fit (Underfitting)\nMSE: {mse_linear:.2f}')
plt.plot(X, y_pred_poly, color='green', linewidth=2, label=f'Polynomial Fit (Degree 2)\nMSE: {mse_poly:.2f}')
plt.title('Demonstrating Underfitting with Linear vs. Polynomial Regression', fontsize=16)
plt.xlabel('Feature X', fontsize=14)
plt.ylabel('Target y', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()

Ausgabe:

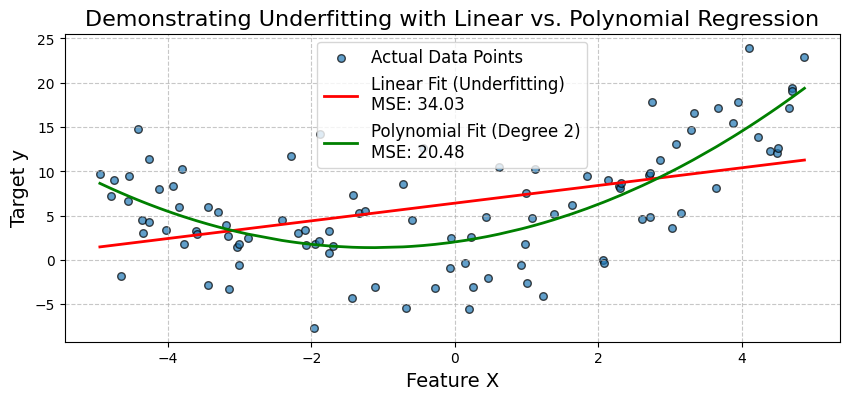
Das Diagramm bestätigt visuell, dass das einfache lineare Modell nicht richtig passt. Es gelingt nicht, die Kurve in den Daten zu erfassen. Das polynomiale Regressionsmodell bietet durch die Einbeziehung des X^2-Terms eine viel bessere Anpassung, was durch den niedrigeren MSE belegt wird.

Dies zeigt, wie die Erweiterung von Merkmalen (Erhöhung der Modellkomplexität) Verzerrungen reduzieren und die Genauigkeit verbessern kann, wenn die zugrunde liegende Beziehung nicht linear ist. Als Nächstes schauen wir uns eine Fallstudie zur medizinischen Diagnose an.

Fallstudie zur medizinischen Diagnose

Simulieren wir ein medizinisches Diagnoseszenario anhand des bekannten Datensatzes Breast Cancer Wisconsin (Diagnostic), der auf scikit-learn verfügbar ist.

Wir werden zunächst versuchen, ein Klassifizierungsmodell zu erstellen, das nur eine sehr begrenzte Anzahl von Merkmalen verwendet, was zu einer Unteranpassung führen kann. Dann werden wir einen umfangreicheren Satz von Merkmalen und möglicherweise einen komplexeren Algorithmus verwenden, um Verbesserungen zu demonstrieren.

Beginnen wir damit, die notwendigen Bibliotheken wie folgt zu importieren:

# Import necessary libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, roc_auc_score, confusion_matrix, ConfusionMatrixDisplay

Jetzt können wir die Daten laden und vorbereiten:

cancer = load_breast_cancer()
X = pd.DataFrame(cancer.data, columns=cancer.feature_names)
y = cancer.target # 0 for malignant, 1 for benign

Zur Veranschaulichung wählen wir eine sehr begrenzte Teilmenge von Merkmalen für das Underfitting-Szenario aus. Diese sind für sich genommen vielleicht nicht besonders aussagekräftig:

features_limited = ['mean texture', 'mean symmetry']
X_limited = X[features_limited]

Für das verbesserte Modell werden wir eine größere Teilmenge (oder alle Merkmale) verwenden. Wählen wir die ersten 10 Merkmale aus, um einen Überblick zu bekommen:

features_comprehensive = cancer.feature_names[:10]
X_comprehensive = X[features_comprehensive]

Lass uns die Daten aufteilen. Der Übersichtlichkeit halber machen wir das für jedes Feature-Set separat:

X_train_lim, X_test_lim, y_train, y_test = train_test_split(X_limited, y, test_size=0.3, random_state=42, stratify=y)
X_train_comp, X_test_comp, _, _ = train_test_split(X_comprehensive, y, test_size=0.3, random_state=42, stratify=y) # y_train and y_test are the same

Lass uns die Merkmale skalieren, denn das ist wichtig für die logistische Regression und viele andere Algorithmen:

scaler_lim = StandardScaler().fit(X_train_lim)
X_train_lim_scaled = scaler_lim.transform(X_train_lim)
X_test_lim_scaled = scaler_lim.transform(X_test_lim)

scaler_comp = StandardScaler().fit(X_train_comp)
X_train_comp_scaled = scaler_comp.transform(X_train_comp)
X_test_comp_scaled = scaler_comp.transform(X_test_comp)

Nun wollen wir eine logistische Regression mit begrenzten Merkmalen anpassen:

print("Scenario 1: Logistic Regression (Limited Features - Potential Underfitting)")
log_reg_limited = LogisticRegression(random_state=42, solver='liblinear') # liblinear is good for small datasets
log_reg_limited.fit(X_train_lim_scaled, y_train)
y_pred_lim = log_reg_limited.predict(X_test_lim_scaled)
y_proba_lim = log_reg_limited.predict_proba(X_test_lim_scaled)[:, 1]

acc_lim = accuracy_score(y_test, y_pred_lim)
auc_lim = roc_auc_score(y_test, y_proba_lim)
print(f"Features used: {features_limited}")
print(f"Accuracy: {acc_lim:.4f}")
print(f"AUC: {auc_lim:.4f}")

Ausgabe:

Scenario 1: Logistic Regression (Limited Features - Potential Underfitting)

Features used: ['mean texture', 'mean symmetry']

Accuracy: 0.7544

AUC: 0.8151

Lass uns eine Strategie zur Schadensbegrenzung entwickeln. Wir werden ein logistisches Regressionsmodell mit mehr Merkmalen anpassen:

print("Scenario 2: Logistic Regression (Comprehensive Features)")
log_reg_comp = LogisticRegression(random_state=42, solver='liblinear')
log_reg_comp.fit(X_train_comp_scaled, y_train)
y_pred_comp_lr = log_reg_comp.predict(X_test_comp_scaled)
y_proba_comp_lr = log_reg_comp.predict_proba(X_test_comp_scaled)[:, 1]

acc_comp_lr = accuracy_score(y_test, y_pred_comp_lr)
auc_comp_lr = roc_auc_score(y_test, y_proba_comp_lr)
print(f"Features used: First 10 features") # For brevity
print(f"Accuracy: {acc_comp_lr:.4f}")
print(f"AUC: {auc_comp_lr:.4f}")

Ausgabe:

Scenario 2: Logistic Regression (Comprehensive Features)

Features used: First 10 features

Accuracy: 0.9181

AUC: 0.9831

Nun wollen wir ein komplexeres Modell wie Random Forest mit mehr Merkmalen anwenden:

print("Scenario 3: Random Forest (Comprehensive Features)")
rf_comp = RandomForestClassifier(random_state=42, n_estimators=100) # n_estimators is a key hyperparameter
rf_comp.fit(X_train_comp_scaled, y_train) # RF can also benefit from scaled data, though less sensitive
y_pred_comp_rf = rf_comp.predict(X_test_comp_scaled)
y_proba_comp_rf = rf_comp.predict_proba(X_test_comp_scaled)[:, 1]

acc_comp_rf = accuracy_score(y_test, y_pred_comp_rf)
auc_comp_rf = roc_auc_score(y_test, y_proba_comp_rf)
print(f"Features used: First 10 features")
print(f"Accuracy: {acc_comp_rf:.4f}")
print(f"AUC: {auc_comp_rf:.4f}")

Ausgabe:

Scenario 3: Random Forest (Comprehensive Features)

Features used: First 10 features

Accuracy: 0.9415

AUC: 0.9878

Lass uns die Konfusionsmatrix für jeden Fall aufzeichnen und vergleichen:

fig, axes = plt.subplots(1, 3, figsize=(20, 5))
fig.suptitle('Comparison of Model Performance (Confusion Matrices on Test Set)', fontsize=16)

# Model 1: Logistic Regression (Limited Features)
cm_lim = confusion_matrix(y_test, y_pred_lim)
disp_lim = ConfusionMatrixDisplay(confusion_matrix=cm_lim, display_labels=cancer.target_names)
disp_lim.plot(ax=axes[0], cmap='Blues')
axes[0].set_title(f'LogReg (Limited Features)\nAcc: {acc_lim:.2f}, AUC: {auc_lim:.2f}')

# Model 2: Logistic Regression (Comprehensive Features)
cm_comp_lr = confusion_matrix(y_test, y_pred_comp_lr)
disp_comp_lr = ConfusionMatrixDisplay(confusion_matrix=cm_comp_lr, display_labels=cancer.target_names)
disp_comp_lr.plot(ax=axes[1], cmap='Greens')
axes[1].set_title(f'LogReg (Comprehensive Features)\nAcc: {acc_comp_lr:.2f}, AUC: {auc_comp_lr:.2f}')

# Model 3: Random Forest (Comprehensive Features)
cm_comp_rf = confusion_matrix(y_test, y_pred_comp_rf)
disp_comp_rf = ConfusionMatrixDisplay(confusion_matrix=cm_comp_rf, display_labels=cancer.target_names)
disp_comp_rf.plot(ax=axes[2], cmap='Oranges')
axes[2].set_title(f'Random Forest (Comprehensive Features)\nAcc: {acc_comp_rf:.2f}, AUC: {auc_comp_rf:.2f}')

plt.tight_layout(rect=[0, 0, 1, 0.96]) # Adjust layout to make space for suptitle
plt.show()

Ausgabe:

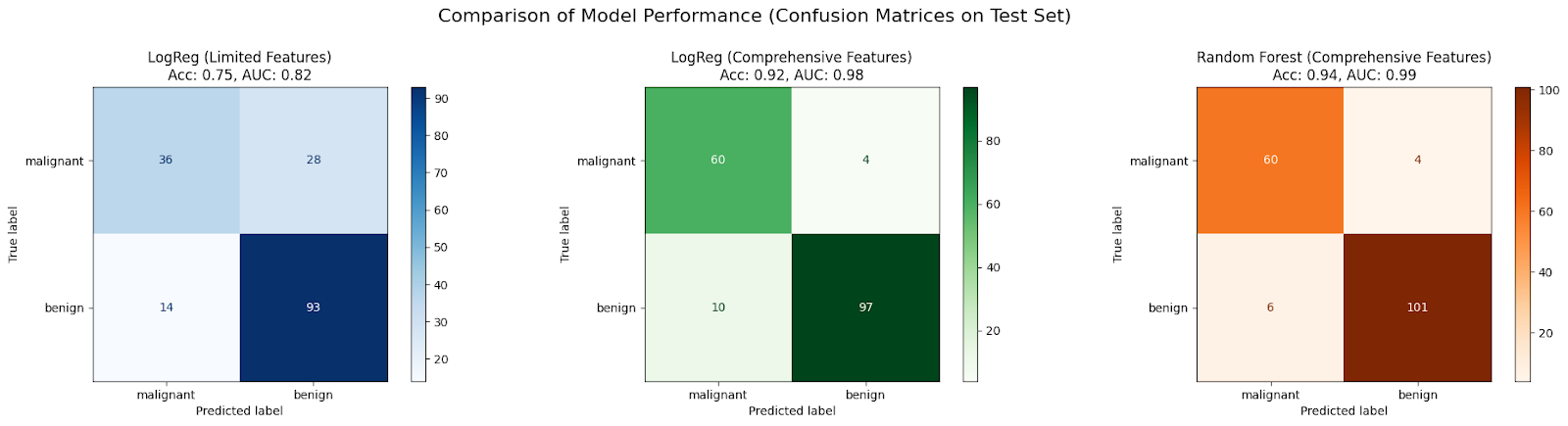
In dieser Fallstudie ist zu erwarten, dass ein anfängliches LogisticRegression Modell, das auf nur zwei Merkmalen (Szenario 1) trainiert wurde, aufgrund unzureichender Informationen zu wenig passt, was zu einer schlechten Genauigkeit und AUC führt.

Die Leistung verbessert sich in der Regel, wenn derselbe Algorithmus einen umfangreicheren Satz von Merkmalen erhält (Szenario 2), da er mehr Daten zum Lernen hat und dadurch weniger verzerrt wird.

Eine weitere Verbesserung wird oft durch die Verwendung eines komplexeren Algorithmus wie RandomForestClassifier mit dem umfassenden Merkmalssatz (Szenario 3) erzielt, da er Nichtlinearitäten und Wechselwirkungen zwischen Merkmalen effektiver erfassen kann, was die Verzerrungen weiter reduziert und die Anpassung des Modells an die Daten verbessert.

Fortgeschrittene Themen und zukünftige Richtungen

Obwohl wir die Grundlagen behandelt haben, entwickelt sich die Landschaft des maschinellen Lernens ständig weiter. Hier ist ein kurzer Blick darauf, wie sich die Unterversorgung auf fortgeschrittenere Bereiche auswirkt.

Die Rolle des Deep Learning

Deep-Learning-Modelle, insbesondere tiefe neuronale Netze mit vielen Schichten, sind für ihre hohe Kapazität bekannt, d.h. sie können theoretisch sehr komplexe Funktionen approximieren.

Aufgrund ihrer inhärenten Komplexität sind Deep-Learning-Modelle in der Regel weniger anfällig für Underfitting als einfachere Modelle, vorausgesetzt, sie werden mit ausreichend Daten richtig trainiert. Ihre Struktur ermöglicht es ihnen, automatisch komplizierte Merkmalsdarstellungen aus Rohdaten (wie Pixel in Bildern oder Wörter in Texten) zu lernen.

Deep Learning ist jedoch nicht immun gegen Probleme, die wie Underfittingaussehen. Wenn ein Netz schlecht konzipiert ist (z. B. unzureichende Tiefe/Breite für die Aufgabe), nicht lange genug trainiert wird oder ungeeignete Aktivierungsfunktionen oder Optimierungsalgorithmen verwendet, kann es trotzdem nicht konvergieren und einen hohen Trainingsfehler aufweisen.

Architektonische Innovationen wie Residualverbindungen (ResNets) und Normalisierungstechniken (Batch Normalization) helfen dabei, sehr tiefe Netze effektiv zu trainieren, indem sie Probleme mit verschwindenden/explodierenden Gradienten abmildern und es ihnen ermöglichen, ihre volle Kapazität zu erreichen, wodurch Konvergenzprobleme vermieden werden, die ein Underfitting imitieren.

Automatisiertes maschinelles Lernen (AutoML)

Die Suche nach dem richtigen Modell, den richtigen Merkmalen und Hyperparametern, um sowohl Underfitting als auch Overfitting zu vermeiden, kann zeitaufwändig sein. AutoML zielt darauf ab, diesen Prozess zu automatisieren.

AutoML-Frameworks können automatisch verschiedene Modelltypen untersuchen (von linearen Modellen bis hin zu komplexen Ensembles und neuronalen Netzen), Feature Engineering und Auswahl durchführen und Hyperparameter optimieren. Durch systematisches Durchsuchen eines riesigen Raums von Möglichkeiten kann AutoML Modellkonfigurationen identifizieren, die eine ausreichende Komplexität aufweisen, um eine Unteranpassung der Daten zu vermeiden.

Methoden wie Neural Architecture Search (NAS) entwerfen automatisch Netzwerkarchitekturen, während ausgefeilte Hyperparameter-Optimierungstechniken (z. B. Bayes'sche Optimierung) effizient gute Hyperparametereinstellungen finden. Diese Tools können den Prozess der Suche nach einem gut passenden Modell erheblich beschleunigen und den manuellen Aufwand für die Diagnose und Korrektur eines unzureichend passenden Modells verringern.

Fazit

Das Dilemma zwischen Underfitting und Overfitting zu verstehen, ist grundlegend für erfolgreiches maschinelles Lernen. Wir haben gesehen, dass Underfitting entsteht, wenn ein Modell zu einfach ist (hohe Verzerrung), um die zugrundeliegenden Trends in den Daten zu erfassen, was zu einer schlechten Leistung sowohl bei Trainings- als auch bei ungesehenen Daten führt. Zu den Hauptursachen gehören unzureichende Modellkomplexität, schlechte Merkmale, unzureichendes Training und übermäßige Regularisierung.

Zur Diagnose der Unteranpassung werden Leistungskennzahlen untersucht, Lernkurven gezeichnet und Modelle verglichen, oft mit Hilfe von Code. Glücklicherweise gibt es mehrere Strategien, um das Underfitting zu beheben: Erhöhung der Modellkomplexität (Auswahl besserer Algorithmen, Erweiterung der Merkmale, Abstimmung der Hyperparameter), Verbesserung der Merkmale (Feature Engineering, Datenanreicherung), Anpassung der Regularisierung und Einsatz leistungsfähiger Ensemble-Methoden, wie in unseren Codebeispielen gezeigt.

Um diese und weitere Techniken anhand praktischer Beispiele kennenzulernen, besuche unseren Grundlagen des maschinellen Lernens in Python Lernpfad.