Programa
Você já sonhou em executar seu próprio ChatGPT diretamente em seu laptop?
Com os rápidos avanços nos modelos de linguagem grande (LLMs), a possibilidade de trazer esses modelos avançados para o hardware do consumidor está se tornando uma realidade.
A chave para desbloquear esse potencial está na quantização, uma técnica que permite reduzir o tamanho desses modelos cada vez maiores para que sejam executados em dispositivos cotidianos com degradação mínima de desempenho- se implementada corretamente!
Neste guia, vamos nos aprofundar no conceito de quantização, explicando como ele funciona e as diferentes possibilidades de quantização de LLMs. Por fim, quantizaremos nosso modelo em duas etapas simples usando a biblioteca Quanto da Hugging Face.
Vamos nos aprofundar! Você pode acompanhar usando o DataCamp DataLab.
O crescimento cada vez maior de modelos de idiomas grandes
À medida que os LLMs evoluíram, sua complexidade cresceu exponencialmente, levando a um aumento significativo no número de parâmetros. Por exemplo, o primeiro modelo GPT, lançado em 2018, tinha 0,11 bilhão de parâmetros. No final de 2019, o GPT-2 expandiu esse número para 1,5 bilhão, e o GPT-3, lançado no final de 2020, disparou para 175 bilhões de parâmetros.
Atualmente, o GPT-4 conta com mais de 1 trilhão de parâmetros. Esse grande aumento representa um desafio: medida que os modelos crescem, também crescem seus requisitos de memória, muitas vezes ultrapassando a capacidade de aceleradores de hardware avançados, como as GPUs.
Essa demanda crescente por memória limita o treinamento e a hospedagem dos modelos para inferência, restringindo, consequentemente, a acessibilidade e a adoção de soluções baseadas em LLM.
Esse crescimento leva a uma necessidade urgente de tornar esses modelos mais acessíveis, reduzindo seu tamanho. Ao alterar a precisão de alguns componentes do modelo, a quantização reduz o espaço de memória do modelo, mantendo níveis de desempenho semelhantes.
O que é quantização?
A quantização é uma técnica de compactação de modelos que converte os pesos e as ativações em um modelo de linguagem grande de valores de alta precisão para valores de menor precisão. Isso significa alterar os dados de um tipo que pode conter mais informações para um que contém menos. Um exemplo típico é a conversão de dados de um número de ponto flutuante de 32 bits para um número inteiro de 8 bits.
A redução do número de bits necessários para cada um dos pesos ou ativações do modelo leva a uma diminuição significativa em seu tamanho total. Consequentemente, a quantização reduz os LLMs para consumir menos memória, exigir menos espaço de armazenamento e torná-los mais eficientes em termos de energia.
Uma analogia eficaz para entender a quantização é a compressão de imagens. As imagens de alta resolução geralmente são compactadas para uso em sites. Isso envolve a redução do tamanho da imagem por meio da remoção de alguns dados ou bits de informação. Embora isso normalmente reduza a qualidade da imagem até certo ponto, também diminui as dimensões da imagem e o tamanho do arquivo, fazendo com que as páginas da Web sejam carregadas mais rapidamente e, ao mesmo tempo, proporcionando uma experiência visual satisfatória.

Esquema de compactação de imagens para carregamento mais rápido em aplicativos como páginas da Web.
Da mesma forma, a quantização de um LLM reduz seus requisitos computacionais, permitindo que ele seja executado em um hardware menos potente e, ao mesmo tempo, ofereça um desempenho adequado. As imagens compactadas são mais fáceis de manusear, assim como os modelos quantizados são mais implementáveis em várias plataformas, embora haja uma pequena compensação em termos de detalhes ou precisão. Como veremos, o processo de quantização também introduz algum ruído.
Teoria da quantização
Normalmente, a quantização é aplicada aos pesos de um modelo de linguagem grande, embora também possa ser aplicada às ativações. Os pesos do modelo são parâmetros em uma rede neural que determinam a força das conexões entre os neurônios em diferentes camadas. Os pesos são essencialmente os coeficientes aprendidos que transformam os dados de entrada à medida que eles passam pela rede.
Os pesos são inicialmente definidos como valores aleatórios e sem significado e ajustados durante o treinamento com base no erro entre a saída prevista e os alvos reais. Esse processo de ajuste é orientado por algoritmos de otimização, como a descida de gradiente.
Se você quiser saber mais sobre os aspectos internos dos LLMs, o curso Desenvolvendo grandes modelos de linguagem é para você!
Uma opção para quantizar um modelo é reduzir a precisão de seus pesos de modelo. Para ilustrar isso, vamos nos concentrar na matriz à esquerda na imagem abaixo, que representa uma matriz 3x3 de pesos com precisão de quatro decimais:
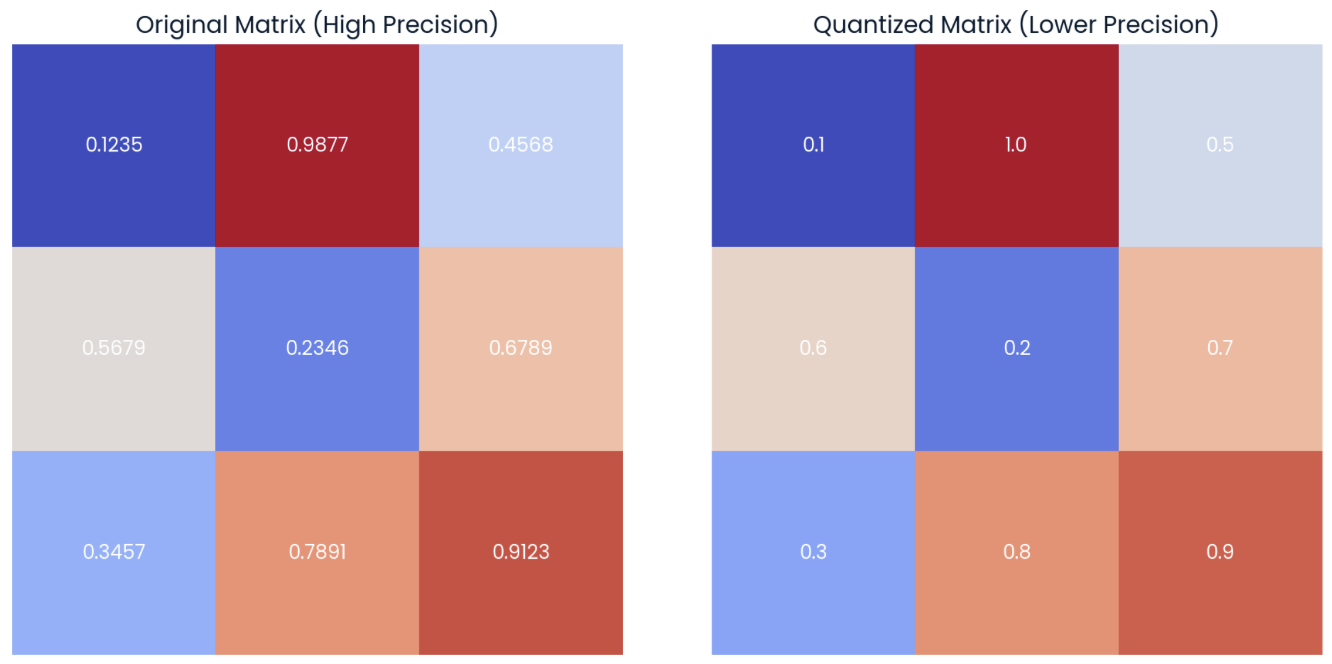
Exemplo de uma matriz aleatória de pesos com precisão de quatro decimais (esquerda) com sua forma quantizada (direita), aplicando o arredondamento para a precisão de uma decimal.
Na matriz à direita, podemos observar a versão quantizada da matriz original. Essa matriz "quantizada" é calculada arredondando os elementos da matriz original para uma casa decimal.
Podemos observar que as matrizes acima não são completamente iguais, mas são muito semelhantes. A diferença de valor por valor é conhecida como erro de quantização, que também pode ser representado em forma de matriz:
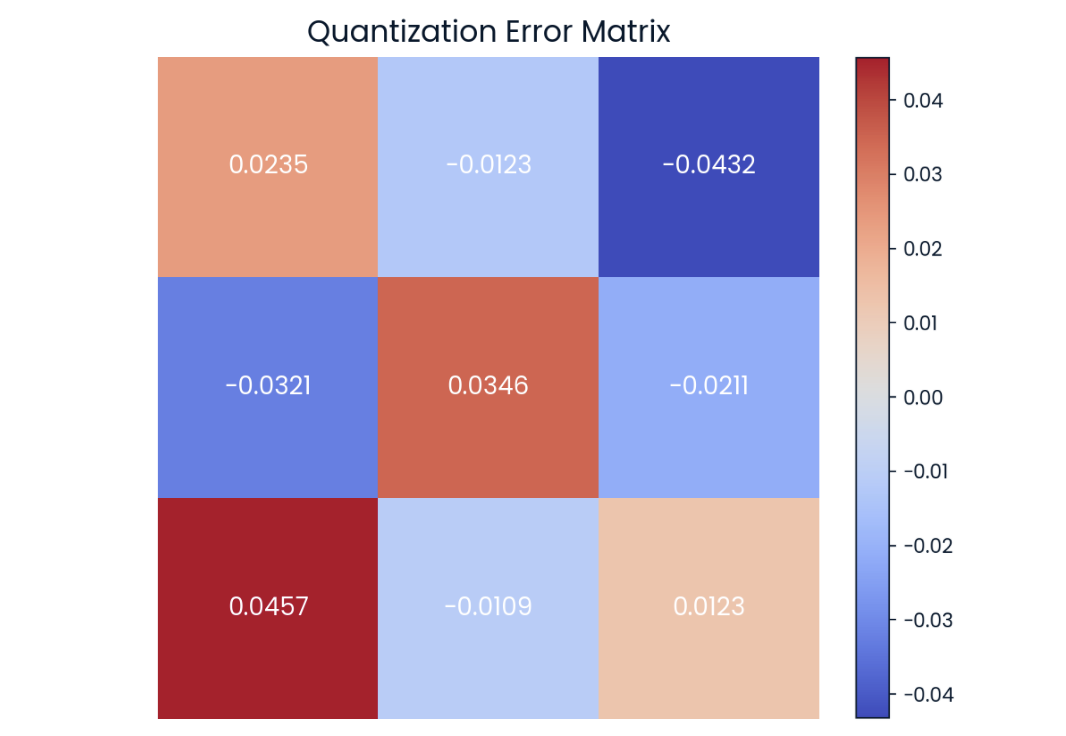
Erro de quantização na matriz de. Quanto mais escura for a cor, maior será o erro.
A pesquisa atual em quantização está concentrada na tentativa de reduzir essa diferença o máximo possível para evitar qualquer degradação do desempenho.
Neste exemplo simples, estamos apenas arredondando os elementos da matriz. Na prática, a quantização é realizada pela conversão de valores numéricos em um tipo de dados diferente, por exemplo, de um tipo de dados de maior precisão para um de menor precisão. Por exemplo, o tipo de dados de armazenamento padrão para a maioria dos modelos é float32.
Nesse caso, precisaríamos alocar 4 bytes por parâmetro (4 vezes a precisão de 8 bits). Portanto, para uma matriz 3x3 como a do exemplo, o espaço total de memória dessa matriz é de 36 bytes.
Se você alterar o tipo de dados - também conhecido como downcasting - para int8, precisaremos apenas de um byte por parâmetro. Portanto, o espaço total de memória da matriz é de 9 bytes.
Ponto flutuante do cérebro - BF16
O tipo de dados selecionado para os pesos do modelo determina o quanto podemos reduzir o modelo. Os tipos tradicionais de ponto flutuante, como float32 e float16, têm sido o padrão em muitos aplicativos de machine learning, proporcionando um equilíbrio entre precisão e eficiência computacional. Especificamente, embora o site float32 ofereça alta precisão e uma ampla faixa dinâmica, ele exige mais memória e potência computacional. Pelo contrário, o site float16 oferece precisão e alcance reduzidos, acelerando significativamente os cálculos.
- Em 2018, o Google reconheceu a necessidade de um formato de ponto flutuante que pudesse oferecer um ponto médio entre a ampla faixa dinâmica do
float32e a ampla faixa dinâmica do float16e a eficiência do float16.
Isso levou à criação do chamado Brain Floating Point (bfloat16), que mantém o intervalo dinâmico de float32 mas com precisão reduzida.
Rebaixamento
Downcasting é o termo formal para a conversão de um tipo de dados de maior precisão em um tipo de dados de menor precisão. Ao usar o downcasting, reduzimos o espaço ocupado na memória e aumentamos a velocidade, pois os cálculos que usam precisão menor também exigem menos memória.
Nesta seção, exploraremos como funciona o downcasting de float32- o tipo de dados de armazenamento padrão para a maioria dos modelos - para o tipo de dados do Google bfloat16do Google, e observaremos como isso normalmente resulta em alguma perda de dados.
Vamos começar definindo um tensor aleatório no PyTorch com elementos do tipo float32 e exibindo os primeiros cinco elementos:
import torch
# random pytorch tensor: float32, size=1000
tensor_fp32 = torch.rand(1000, dtype = torch.float32)
print(tensor_fp32[:5])
>> tensor([0.2257, 0.0480, 0.8520, 0.3115, 0.1373])Agora podemos reduzir o tensor para bfloat16 usando o método .to(dtype) e observar os primeiros 5 novos elementos:
# downcast the tensor to bfloat16 using the "to" method
tensor_fp32_to_bf16 = tensor_fp32.to(dtype = torch.bfloat16)
print(tensor_fp32_to_bf16[:5])
>> tensor([0.2256, 0.0481, 0.8516, 0.3105, 0.1377], dtype=torch.bfloat16)Como podemos ver, os valores são bem próximos, embora não sejam os mesmos. A diferença se torna mais perceptível quando começamos a realizar operações nos valores. Por exemplo, ao multiplicar o tensor original por ele mesmo:
# tensor_fp32 x tensor_fp32
m_float32 = torch.dot(tensor_fp32, tensor_fp32)
print(m_float32)
>> tensor(322.1082)Se fizermos o mesmo cálculo com o tensor quantizado, veremos que a diferença é maior:
# tensor_fp32_to_bf16 x tensor_fp32_to_bf16
m_bfloat16 = torch.dot(tensor_fp32_to_bf16, tensor_fp32_to_bf16)
print(m_bfloat16)
>> tensor(256., dtype=torch.bfloat16)Podemos observar uma clara diferença entre os resultados finais devido à propagação de erros.
O mesmo efeito de propagação de erros ao operar com tensores quantizados ocorre ao fazer o downcasting de LLMs, o que leva a uma perda de informações. Como vimos, o uso de menos memória implica que o cálculo pode ser menos preciso. O efeito da multiplicação é semelhante ao da propagação de erros reais camada por camada, que se acumula e acaba afetando algumas previsões de tokens.
Com o downcasting, o desempenho permanece aceitável ao usar o tipo bfloat16 mas isso não se aplica a tipos de dados menores.
O Downcasting não é comumente usado como uma técnica de quantização eficaz devido a essa restrição nos tipos de dados. Em vez disso, são usados outros métodos que mantêm o desempenho mais próximo do modelo original, convertendo-o de volta para float32 durante a inferência.
Tipos de quantização
Há vários tipos de quantização, e descrevemos cada um deles em detalhes a seguir:
Quantização linear
A quantização linear é um dos esquemas de quantização mais populares para LLMs. Em termos simples, isso envolve o mapeamento do intervalo de valores de ponto flutuante dos pesos originais para um intervalo de valores de ponto fixo uniformemente, usando o tipo de dados de alta precisão para inferência.
Para simplificar ao máximo, vamos analisar as etapas necessárias para aplicar a quantização linear a um modelo. Observe que as fórmulas reais são mostradas na imagem abaixo:
- Calcule os valores mínimo e máximo: Para cada tensor, precisamos obter os valores mínimo e máximo para definir o intervalo dos valores de ponto flutuante a serem quantizados. O tipo de dados para o qual você deseja converter fornecerá o mínimo e o máximo do intervalo quantizado. Por exemplo, no caso de um número inteiro sem sinal, o intervalo seria de 0 a 255 para 8 bits.
- Calcule a escala (
s) e o ponto zero (s): A escala ajusta o intervalo de valores de ponto flutuante para que se encaixem no intervalo de números inteiros. O ponto zero garante que zero no intervalo de ponto flutuante seja representado com precisão por um número inteiro, mantendo a precisão e a estabilidade numéricas, especialmente para valores próximos de zero. - Quantize os valores (
q): Essa etapa envolve o mapeamento de valores de ponto flutuante para um intervalo de inteiros de precisão inferior usando um fator de escala s e um ponto zero s calculado na etapa anterior. A operação de arredondamento garante que o resultado final seja um número inteiro discreto, adequado para armazenamento e computação em formatos de precisão inferior. - Desquantizar: Durante a inferência, os valores dequantizados são usados para cálculos a fim de obter maior precisão, embora apenas os pesos quantizados sejam armazenados. Essa etapa também permitirá que você calcule o erro de quantização.
Vamos associar cada uma das etapas descritas acima com sua fórmula correspondente:

Equações de quantização usadas para aplicar quantização linear a qualquer matriz de pesos.
É difícil para você imaginar como aplicar essas fórmulas? Vamos colocar a mão na massa!
Se aplicarmos essas fórmulas ao tensor de peso 3x3 à esquerda na imagem abaixo, obteremos a matriz quantizada mostrada à direita. Recomendo que você dedique alguns minutos para calcular os valores máximo e mínimo do intervalo quantizado e alguns dos valores quantizados:
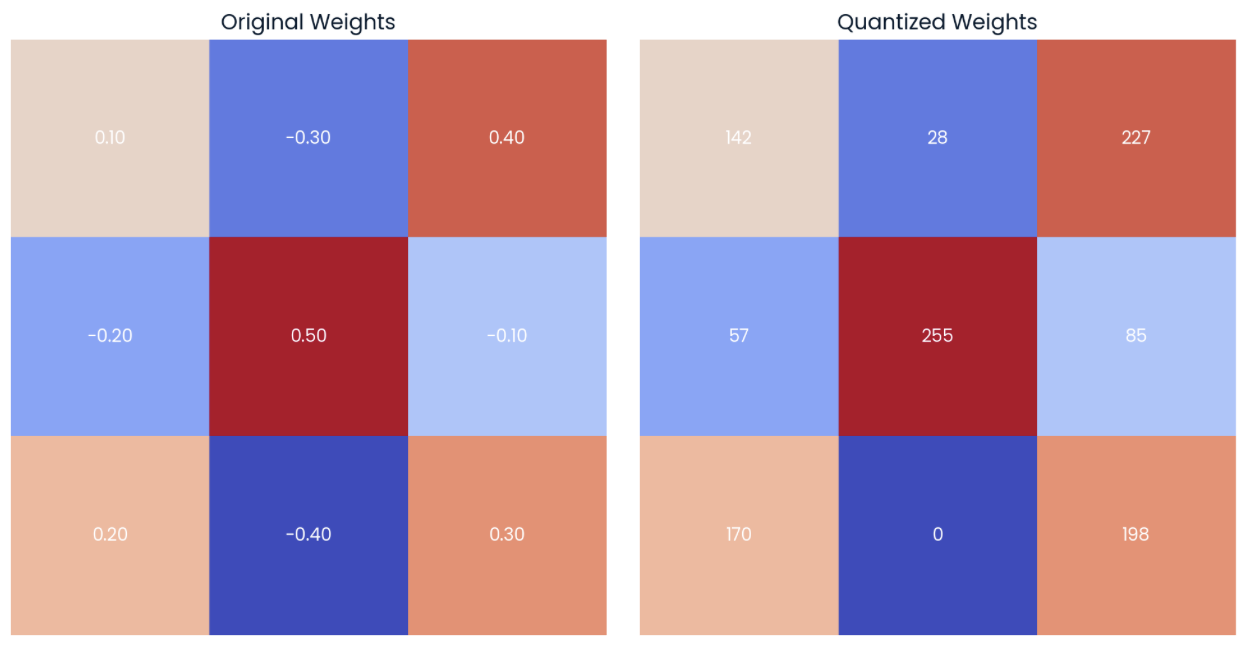
Exemplo de uma matriz aleatória de pesos com precisão de duas casas decimais (esquerda) com sua forma quantizada (direita) para int8 tipo de dados.
Podemos ver que o limite inferior do valor de int8 corresponde ao valor mais baixo do tensor original (-0.40 → 0), enquanto o limite superior corresponde ao valor mais alto do tensor original (0.50 → 255).
Se agora dequantizarmos os valores usando a fórmula (4), poderemos ver que os valores dequantizados estão próximos dos valores originais (matriz à esquerda). Podemos computar o erro de quantização calculando a diferença ponto a ponto (matriz à direita):
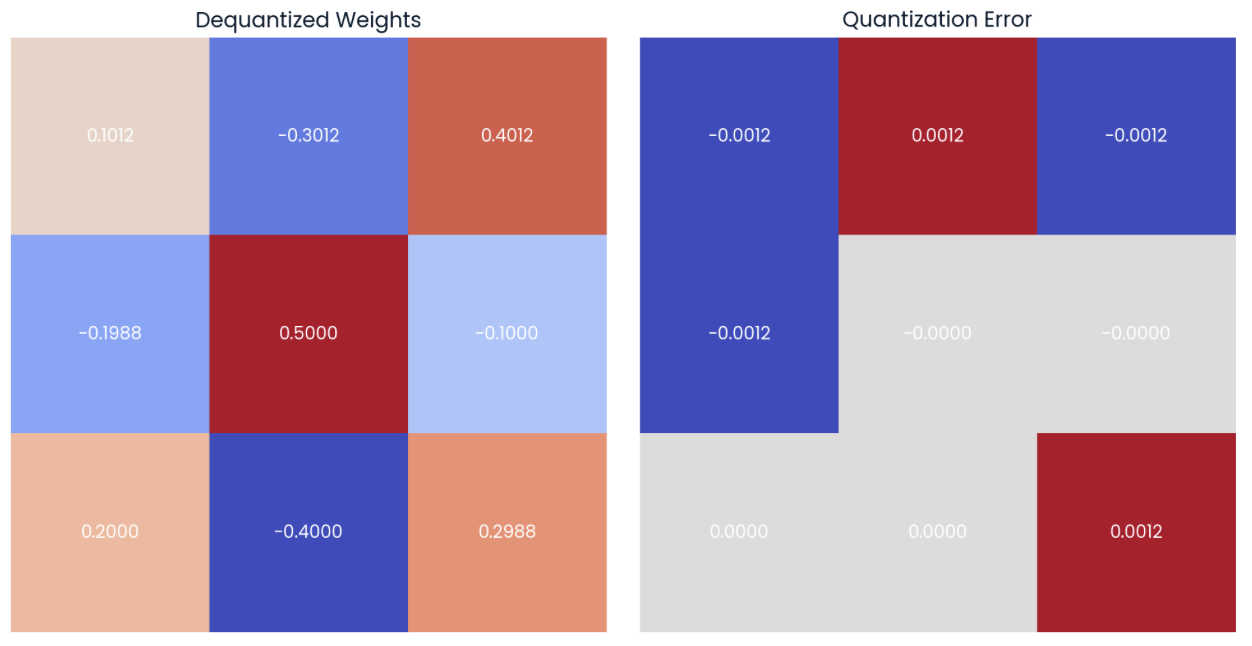
Os valores podem ser dequantizados usando os pesos quantizados e os valores de escala e de ponto zero (esquerda). A diferença ponto a ponto ou o erro de quantização pode ser calculado (à direita).
A quantização linear reduz o tamanho do modelo armazenando apenas os pesos quantizados e os valores de escala e de ponto zero na memória, enquanto os utiliza para calcular os pesos originais para inferência e manter o desempenho.
Quantização em sentido horário
A quantização linear é uma opção popular devido à sua simplicidade, mas há várias maneiras de criar um mapeamento. Outro método bastante popular atualmente é aquantização Blockwise, que é mais precisa do que a quantização linear para modelos com distribuições de peso não uniformes.
A quantização em sentido horário é um método mais sofisticado que envolve a quantização de pesos em blocos menores em vez de em todo o intervalo. Esse método se baseia em dois conceitos-chave:
- Quantização em sentido horário: Os pesos são divididos em blocos menores, e a quantização é aplicada a cada bloco separadamente. Isso permite um melhor tratamento das variações em diferentes partes do modelo.
- Blocos com reconhecimento de distribuição: O processo de quantização leva em conta a frequência relativa dos pesos dentro de cada bloco, criando blocos que estão cientes da distribuição dos pesos. Isso resulta em um mapeamento mais eficiente dos valores.
Quantização de peso vs. quantização de ativação
Em nossos exemplos de matriz, concentramo-nos principalmente no processo de quantização dos pesos de um modelo. Embora a quantização do peso seja uma etapa crucial para a otimização do modelo, também é importante considerar que as ativações de um modelo também podem ser quantizadas.
Quantização da ativação refere-se ao processo de redução da precisão das saídas intermediárias de cada camada da rede. Ao contrário dos pesos, que são estáticos (constantes) depois que o modelo é treinado, as ativações são dinâmicas. Isso significa queas ativações do mudam a cada entrada na rede, o que dificulta a previsão de seu alcance.
Em geral, a quantização de ativação é mais difícil de implementar do que a quantização de peso. Isso requer uma calibração cuidadosa para garantir que o intervalo dinâmico das ativações seja bem capturado.
A quantização de peso e a quantização de ativação são técnicas complementares. Ao aplicar as duas técnicas, podemos permitir melhorias significativas no tamanho do modelo sem comprometer muito o desempenho.
Quantização pós-treinamento (PTQ) vs. treinamento com reconhecimento de quantização (QAT)
A quantização também pode ser realizada em diferentes pontos no tempo. Se pegarmos um modelo pré-treinado e quantizarmos os parâmetros do modelo durante a fase de inferência, estaremos realizando a Quantização Pós-Treinamento (PTQ).
Esse método não envolve nenhuma alteração no processo de treinamento em si. A faixa dinâmica dos parâmetros é recalculada no tempo de execução, da mesma forma como trabalhamos com as matrizes de exemplo.
Por outro lado, há também a opção de aplicar o treinamento com reconhecimento de quantização (QAT). Essa abordagem envolve a modificação do processo de treinamento para simular os efeitos da quantização durante o treinamento. O modelo é treinado para ser resistente ao ruído de quantização, o que resulta em melhor precisão.
Durante o QAT, os estados intermediários do treinamento contêm uma versão quantizada dos pesos e os pesos originais não quantizados (também na memória!). Portanto, usamos a versão quantizada do modelo para inferência, mas a versão não quantizada dos pesos do modelo será atualizada durante a retropropagação.
Como esperado, embora mais complexo e demorado, o QAT geralmente resulta em maior precisão em comparação com o PTQ.
Técnicas de calibração
Alguns métodos de quantização exigem uma etapa de calibração. Por exemplo, precisamos determinar o intervalo de ativação original de um modelo antes da quantização. A calibração geral geralmente envolve a execução de inferência em um conjunto de dados representativo para otimizar os parâmetros de quantização e minimizar o erro de quantização.
Durante esse processo de calibração, o algoritmo de quantização coleta estatísticas sobre a distribuição e o intervalo das ativações e pesos do modelo. Essas estatísticas ajudam a determinar os melhores parâmetros de quantização. O cálculo da escala e do ponto zero ao quantificar os pesos também é um tipo de calibração, mas há outros tipos:
- Calibração de percentis: Concentra-se em um intervalo de percentil especificado dos pesos, ignorando os valores extremos, o que leva a uma quantização mais robusta.
- Calibração da média e do desvio padrão: Define o intervalo de quantização com base nas medidas estatísticas da média e do desvio padrão dos pesos.
No entanto, métodos de quantização como QLoRA podem ser usados sem nenhuma etapa de calibração.
Em geral, esses métodos substituem todas as camadas lineares do modelo por camadas lineares quantizadas (QLinear). As camadasQLinear são projetadas para lidar com a quantização internamente, eliminando assim a necessidade de uma etapa de calibração adicional. Isso torna o processo de quantização mais simples de implementar e, ao mesmo tempo, mantém o desempenho do modelo.
Ferramentas para quantificação
Várias ferramentas e bibliotecas em Python oferecem suporte à quantização, fornecendo ferramentas para PTQ e QAT. Por exemplo, pytorch e tensorflow fornecem métodos de quantização, embora a integração perfeita da quantização nos modelos existentes exija um conhecimento profundo das bibliotecas e dos elementos internos do modelo. Consulte opções de quantização na documentação oficial do PyTorch.
Se você estiver interessado em aprender essas estruturas avançadas, recomendo o curso Aprendizagem profunda em Python.
Até o momento, minha opção favorita para implementar a quantização em etapas fáceis é o Quanto da Hugging Face, que foi projetada para simplificar o processo de quantização dos modelos PyTorch.
Etapas práticas para quantificar um modelo
Um fluxo de trabalho de quantização típico usando a biblioteca Quanto da Hugging Face consistiria nas seguintes etapas:
1. Selecione e carregue um modelo pré-treinado e seu tokenizador correspondente. Nesse caso, usaremos o Pythia 410M da EuletherAI:
from transformers import AutoModelForCausalLM, AutoTokenizer
model_name = "EleutherAI/pythia-410m"
model = AutoModelForCausalLM.from_pretrained(model_name,
low_cpu_mem_usage=True)
tokenizer = AutoTokenizer.from_pretrained(model_name)O método model.gpt_neox pode ajudar você a visualizar as diferentes camadas do modelo carregado:
print(model.gpt_neox)
Esquema de camada por camada do modelo original. O modelo é composto de diferentes tipos de camadas, como camadas lineares e camadas de normalização.
Podemos verificar se o modelo funciona corretamente executando algumas inferências de teste. Por exemplo,
text = "Once upon a time, there was a"
inputs = tokenizer(text, return_tensors="pt")
outputs = model.generate(**inputs, max_new_tokens=10)
print(tokenizer.decode(outputs[0], skip_special_tokens=True))
Além disso, como a quantização do modelo nos permitirá reduzir seu tamanho, também é interessante verificar o tamanho do modelo original antes de iniciar o processo:
import torch
module_sizes = compute_module_sizes(model)
print(f"The model size is {module_sizes[''] * 1e-9} GB")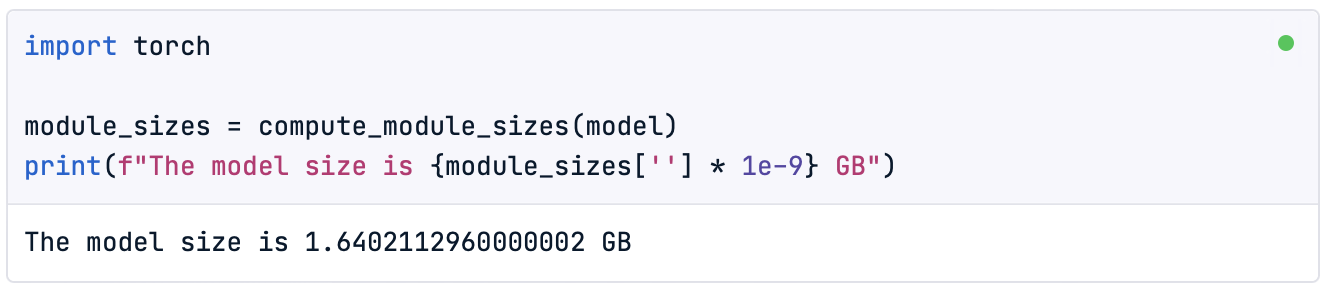
Observação: No DataCamp DataLab você pode encontrar o método implementado. você pode encontrar o método compute_module_sizes() implementado.
Por fim, também podemos visualizar os tensores densos do modelo original da seguinte forma:
print(model.gpt_neox.layers[0].attention.dense.weight)
Como podemos observar, ela se assemelha à matriz não quantizada com a qual trabalhamos neste artigo.
2. Quantizar. O método quantize() permite a conversão do modelo padrão de flutuação padrão em um modelo quantizado imediatamente.
from quanto import quantize, freeze
quantize(model, weights=torch.int8, activations=None)Nesse caso, estamos quantizando apenas os pesos do modelo para um tipo de dadosint8. Esse método converte o modelo para usar aritmética de precisão inferior, incluindo a etapa de calibração.
Se agora imprimirmos as camadas do modelo, veremos que as camadas lineares originais (Linear) foram substituídas por camadas lineares quantizadas (QLinear):
print(model)
Esquema de camada por camada do modelo quantizado. Observe como todas as camadas lineares originais se transformaram em camadas lineares quantizadas ( QLinear).
No entanto, se imprimirmos a matriz de pesos, veremos que eles não foram transformados:
print(model.gpt_neox.layers[0].attention.dense.weight)
3. Congelar. Para aplicar o efeito de quantização aos pesos, precisamos usar o método freeze().
freeze(model)Esse método incorpora os parâmetros de quantização no modelo, convertendo efetivamente os pesos para o tipo de dados de destino. Vamos observar agora os parâmetros do modelo quantizado:
print(model.gpt_neox.layers[0].attention.dense.weight)
Como você pode ver, os pesos agora estão dentro do intervalo do tipo de dados Pytorch int8 do Pytorch.
4. Verificações finais. Depois que o modelo é quantizado, podemos verificar o novo tamanho reduzido do modelo:
module_sizes = compute_module_sizes(model)
print(f"The model size is {module_sizes[''] * 1e-9} GB")
Conseguimos um modelo que tem apenas 35% do tamanho original!
Por fim, vamos verificar o novo desempenho do modelo com uma inferência simples:
outputs = model.generate(**inputs, max_new_tokens=10)
print(tokenizer.decode(outputs[0], skip_special_tokens=True))
É claro que verificar o desempenho com uma única inferência não é significativo, portanto, seria uma boa prática definir um método quantitativo para avaliá-lo.
Agora é a sua vez de experimentar!
Conclusão
As crescentes demandas de memória dos LLMs limitam seu treinamento e hospedagem para inferência, restringindo, consequentemente, a acessibilidade e a adoção de aplicativos baseados em LLM.
Neste artigo, apresentamos o conceito de quantização, que envolve a redução da precisão dos pesos e ativações do modelo para diminuir o espaço ocupado na memória e os requisitos computacionais. Esse processo ajuda a tornar os modelos mais eficientes e acessíveis, especialmente para implantação em dispositivos com recursos limitados.
Abordamos essa técnica usando alguns exemplos, arredondando os valores numéricos dos pesos. Em seguida, passamos para um tipo simples de quantização conhecido como downcasting. Ao fazer o downcasting de um modelo, os parâmetros são convertidos em um tipo de dados mais compacto, como bfloat16para inferência. Embora isso permita que o modelo execute cálculos e ativações nesse tipo de dados menor, o desempenho normalmente diminui com o tamanho do tipo de dados, sendo ineficaz com tipos inteiros como int8.
Para resolver isso, introduz imosa quantização linear, que mantém o desempenho mais próximo do modelo original, convertendo de volta para float32 durante a inferência. Isso permite o uso de tipos de dados ainda menores, como int8.
Percorremos as etapas numéricas da aplicação da quantização linear e implementamos nossa quantização de peso usando a bibliotecaQuanto da Hugging Face. Notavelmente, com a biblioteca Quanto, podemos quantizar qualquer modelo PyTorch, incluindo aqueles disponíveis no Hugging Face.
Para os interessados em experimentar modelos mais pesados, como o LLaMa 2 ou Mistralconsidere a possibilidade de atualizar seu espaço DataCamp para premium para obter mais poder de computação.
![]()
Para modelos maiores, talvez sejam necessários recursos adicionais que não podem ser acessados no Plano Premium da DataCamp.
Ao dominar as técnicas de quantização, podemos liberar todo o potencial dos modelos de linguagem grandes e, ao mesmo tempo, exigir menos recursostornando a IA avançada mais eficiente, acessível e versátil.
Espero que este artigo ajude você a colocar a mão na massa com a quantização para LLMs!
Perguntas frequentes sobre a quantização do LLM
O QAT é melhor do que o PTQ?
O QAT geralmente leva a um melhor desempenho, pois o modelo aprende a ser resistente ao ruído de quantização. No entanto, ele requer mais memória durante o treinamento porque mantém os pesos quantizados e não quantizados.
A biblioteca Quanto permite apenas a quantização pós-treinamento?
Não, a biblioteca Quanto também oferece suporte a métodos avançados para treinamento com reconhecimento de quantização.
A biblioteca Quanto evita a etapa de calibração?
Não, a funçãoquantize() executa uma etapa de calibração implícita. A biblioteca Quanto também oferece ummétodo calibration()para calibrações personalizadas.
Podemos quantizar modelos usando tipos de dados com precisão menor que int8?
Sim, existem modelos de desempenho quantizados para int4 ou até mesmo int2.
Como podemos acessar outros modelos no Hugging Face?
Para acessar outros modelos, basta alterar o nome do modelo para o desejado na página Hugging Face. Observe que você precisa aprovar os termos e condições na página do Hugging Face para acessar determinados modelos.

