Função Tanh: Por que os resultados centrados em zero são importantes para as redes neurais

Sua rede neural tá com 60% de precisão e você não consegue entender por quê?

Você ajustou a taxa de aprendizagem, adicionou mais camadas e brincou com o tamanho do lote. Nada funciona. A perda de treinamento quase não muda depois das primeiras épocas. Você começa a questionar toda a sua configuração. Talvez os dados estejam errados, talvez a arquitetura esteja errada. Mas o que realmente está acontecendo é que sua função de ativação está empurrando todas as saídas em uma direção, o que torna impossível para a rede aprender padrões equilibrados.

A tangente hiperbólica (Tanh) resolve isso centralizando os resultados em torno de zero, variando de -1 a 1. Isso ajuda seus modelos a convergirem mais rápido e mantém os gradientes fluindo simetricamente durante a retropropagação.

Neste artigo, você vai aprender o que é tanh, como funciona matematicamente, quando usá-la em vez de ReLU ou sigmoid e como implementá-la no PyTorch. Se você é novo no mundo do aprendizado profundo, dê uma olhada no nosso guia detalhado sobre funções de ativação em redes neurais.

O que é a função Tanh?

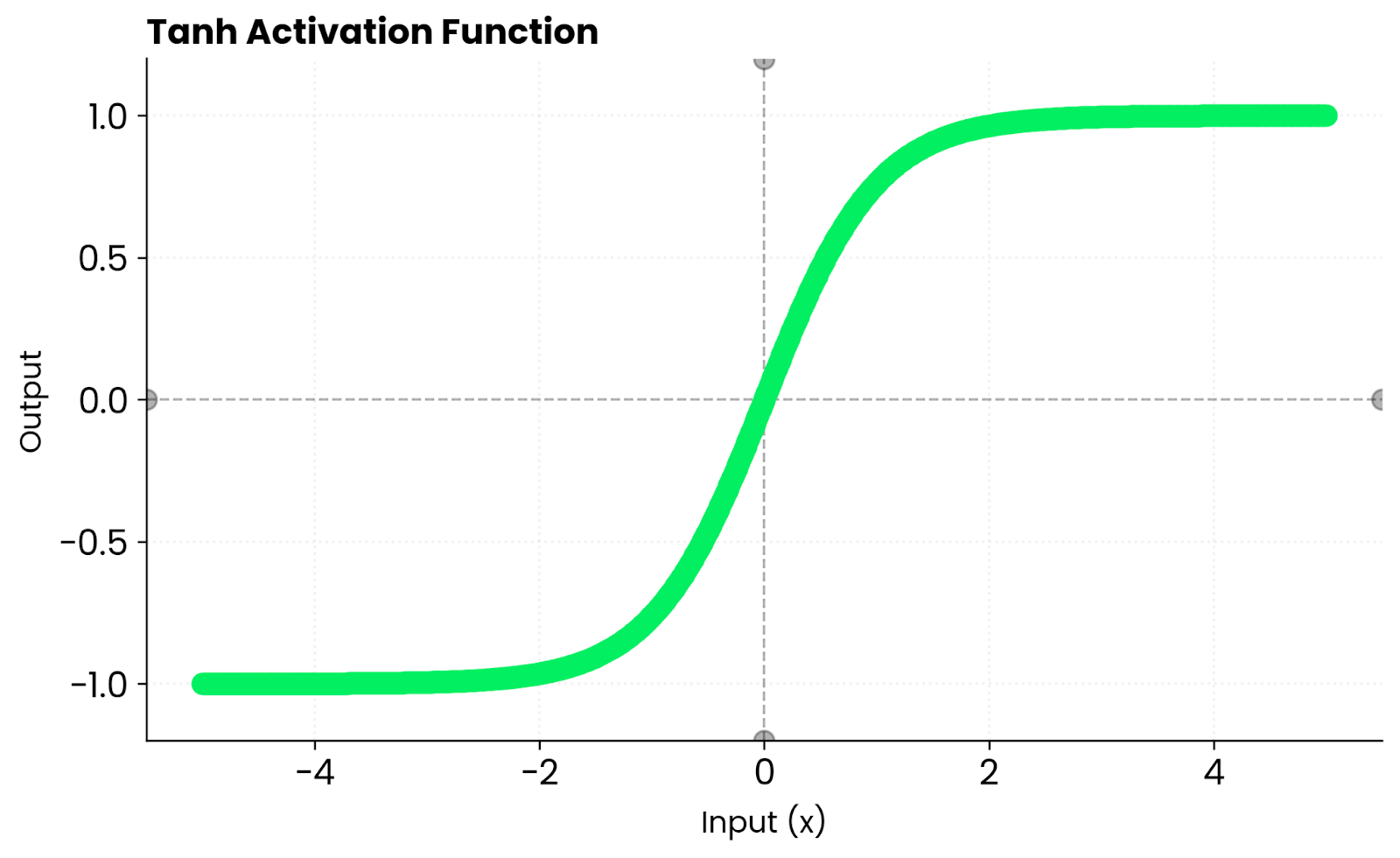
A função tanh transforma qualquer entrada num valor entre -1 e 1.

É uma curva suave em forma de S definida por esta fórmula:

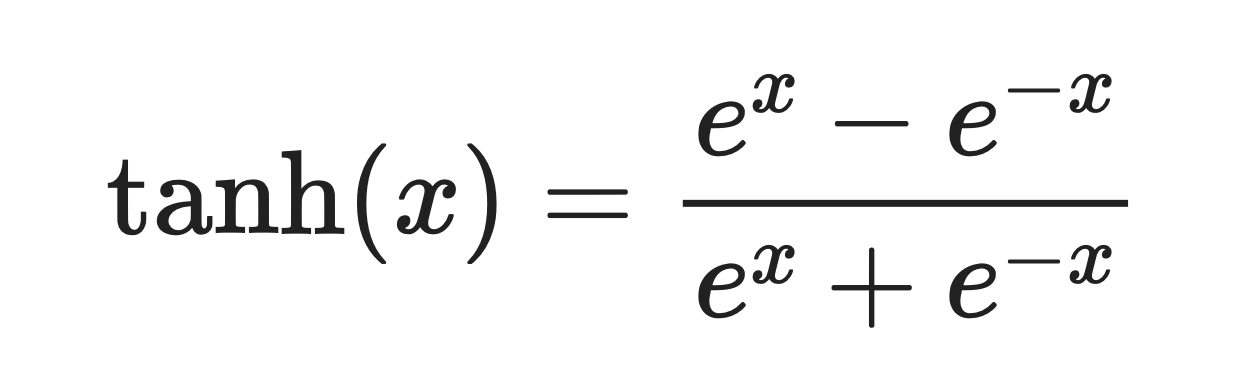
Função Tanh. Imagem do autor

A função se comporta de maneira previsível em situações extremas. Quando você coloca um número positivo grande, ele mostra algo perto de 1. Para um número negativo grande, você vai ter algo próximo de -1.

Perto de zero, a função tanh se comporta quase linearmente. Isso quer dizer que os gradientes fluem suavemente durante a retropropagação, em vez de ficarem comprimidos ou distorcidos.

Para comparar, a sigmoide só mostra valores positivos entre 0 e 1. O Tanh mostra números positivos e negativos. Ele mantém as ativações equilibradas em torno de zero, o que ajuda a otimização a convergir mais rápido em várias arquiteturas de rede.

Você vai ver o tanh sendo usado mais nas redes recorrentes e em qualquer lugar onde as ativações centradas melhoram a estabilidade.

Propriedades matemáticas e computacionais

O Tanh tem algumas propriedades matemáticas que todo aspirante a engenheiro de machine learning precisa saber.

Suave e diferenciável

Tanh é infinitamente diferenciável e suave em todos os lugares.

Isso é importante para a otimização baseada em gradiente. Você não vai encontrar cantos agudos como acontece com o ReLU, onde a derivada salta instantaneamente de 0 para 1. Gradientes suaves significam atualizações de peso mais previsíveis durante a retropropagação.

Saída centrada em zero

A sigmoide gera valores entre 0 e 1. O Tanh mostra valores entre -1 e 1.

Quando as ativações ficam equilibradas em torno de zero, sua rede converge mais rápido. As atualizações de peso não ficam tendenciosas em uma direção, e os gradientes fluem de forma mais uniforme pelas camadas.

Limitado e estável

A faixa de saída do Tanh está fixada entre -1 e 1.

Esses limites evitam a instabilidade numérica. Se você estiver trabalhando com redes que não conseguem lidar com ativações explosivas, o tanh mantém tudo sob controle sem recortes ou manuseio especial.

Comportamento em situações extremas

Para valores positivos grandes, tanh se aproxima de 1. Para valores negativos grandes, ele se aproxima de -1.

Essa simetria mantém as ativações centralizadas e evita a mudança de viés que você vê em funções não centralizadas em zero, como a sigmoidal. Em redes profundas, essa propriedade ajuda as atualizações de peso a se espalharem de forma mais uniforme pelas camadas — sua rede não desenvolve uma preferência por valores positivos ou negativos.

Derivada de tanh

A derivada de tanh é:

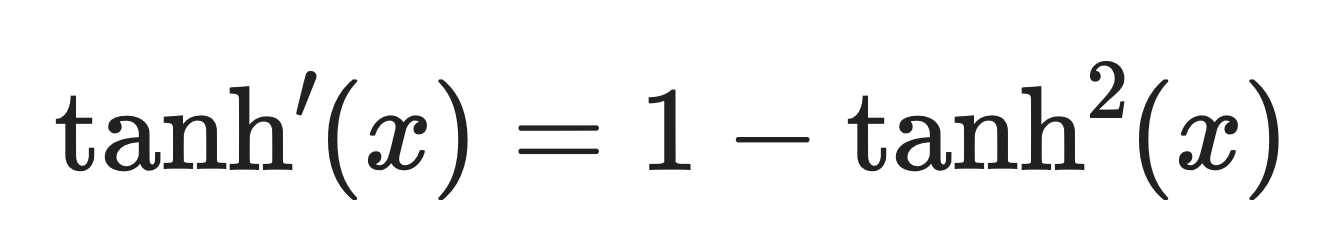
Derivado de Tanh. Imagem do autor.

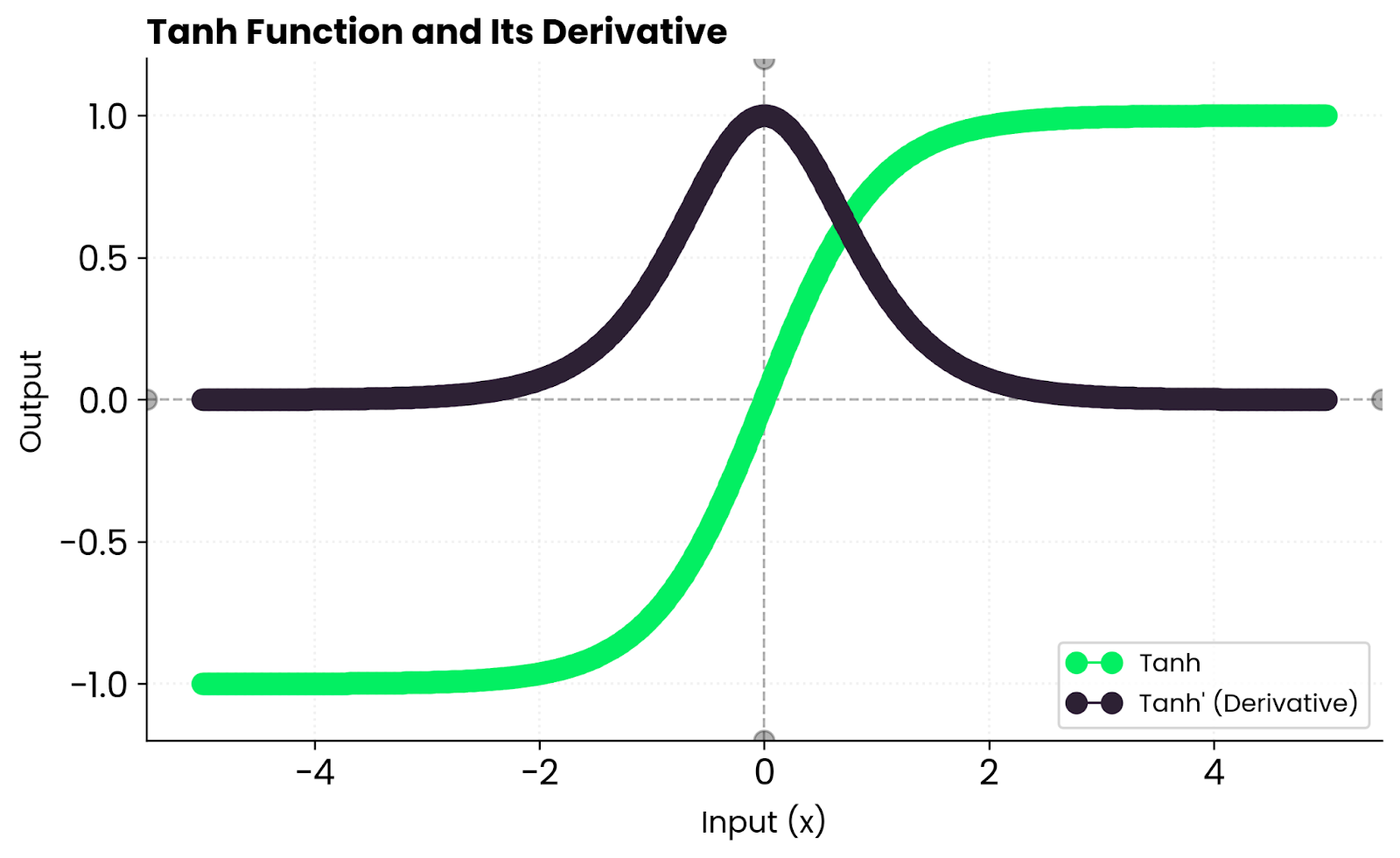
Isso quer dizer que os gradientes são fortes perto de zero, mas diminuem em direção às bordas à medida que a função fica saturada. Quando tanh(x) está perto de 1 ou -1, a derivada se aproxima de zero, o que diminui o aprendizado desses neurônios.

Na prática, você consegue um aprendizado estável para entradas moderadas, mas pode ter gradientes que desaparecem quando as entradas são muito grandes ou muito pequenas. É por isso que as redes profundas geralmente preferem ReLU - ele não fica saturado para valores positivos.

Tanh vs. Outras funções

A Tanh não é a única função de ativação que existe, e entender como ela se compara às alternativas ajuda você a escolher a mais adequada para sua rede.

Sigmoid é um parente próximo do tanh. Na verdade, tanh é só uma versão escalonada e deslocada da sigmoide:

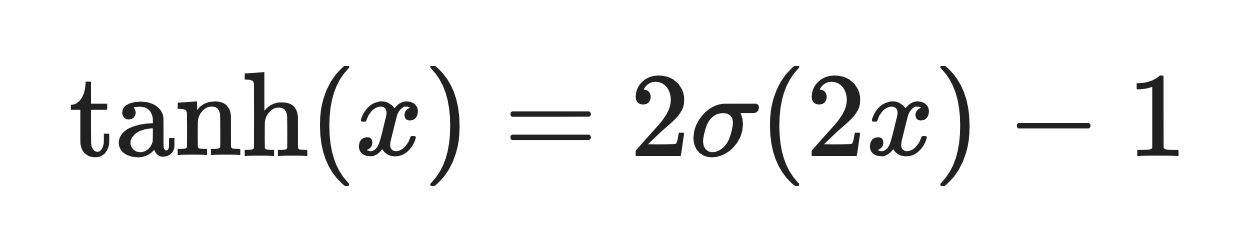
Onde σ(x) é a função sigmoide.

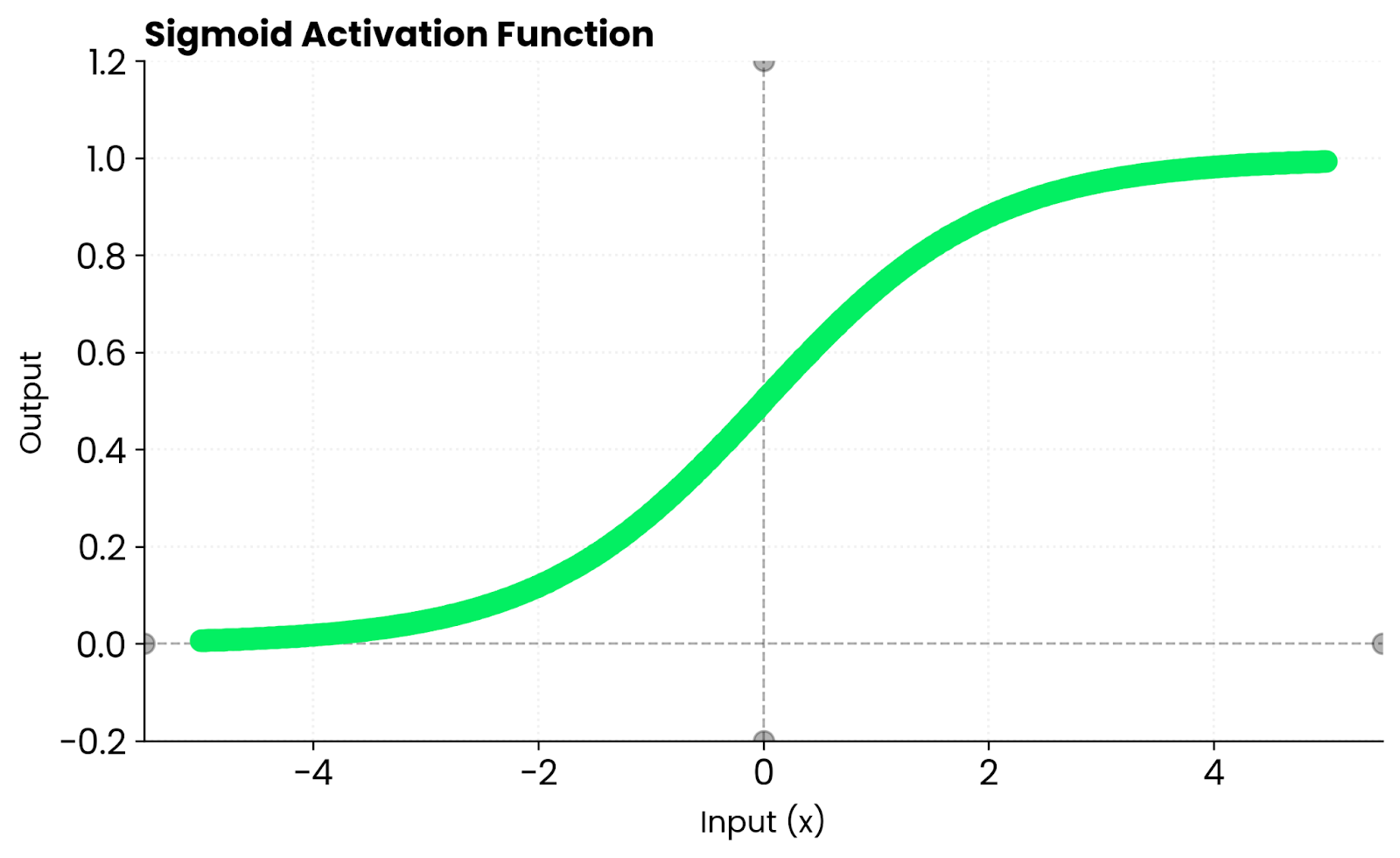
Função sigmoide. Imagem do autor

A principal diferença é que a função sigmoide gera valores entre 0 e 1, enquanto a função tanh gera valores entre -1 e 1. Essa centralização no zero faz com que a função tanh converja mais rápido na maioria dos casos.

O ReLU usa uma abordagem diferente. Ele gera zero para entradas negativas e passa entradas positivas sem alterações. Isso cria escassez, o que significa que muitos neurônios ficam inativos, o que acelera o treinamento. Mas o ReLU acaba com os gradientes para valores negativos. O Tanh não tem esse problema porque mantém gradientes diferentes de zero para entradas negativas. Ele fica saturado nos dois extremos, o que pode atrasar o aprendizado quando as entradas ficam muito grandes ou muito pequenas.

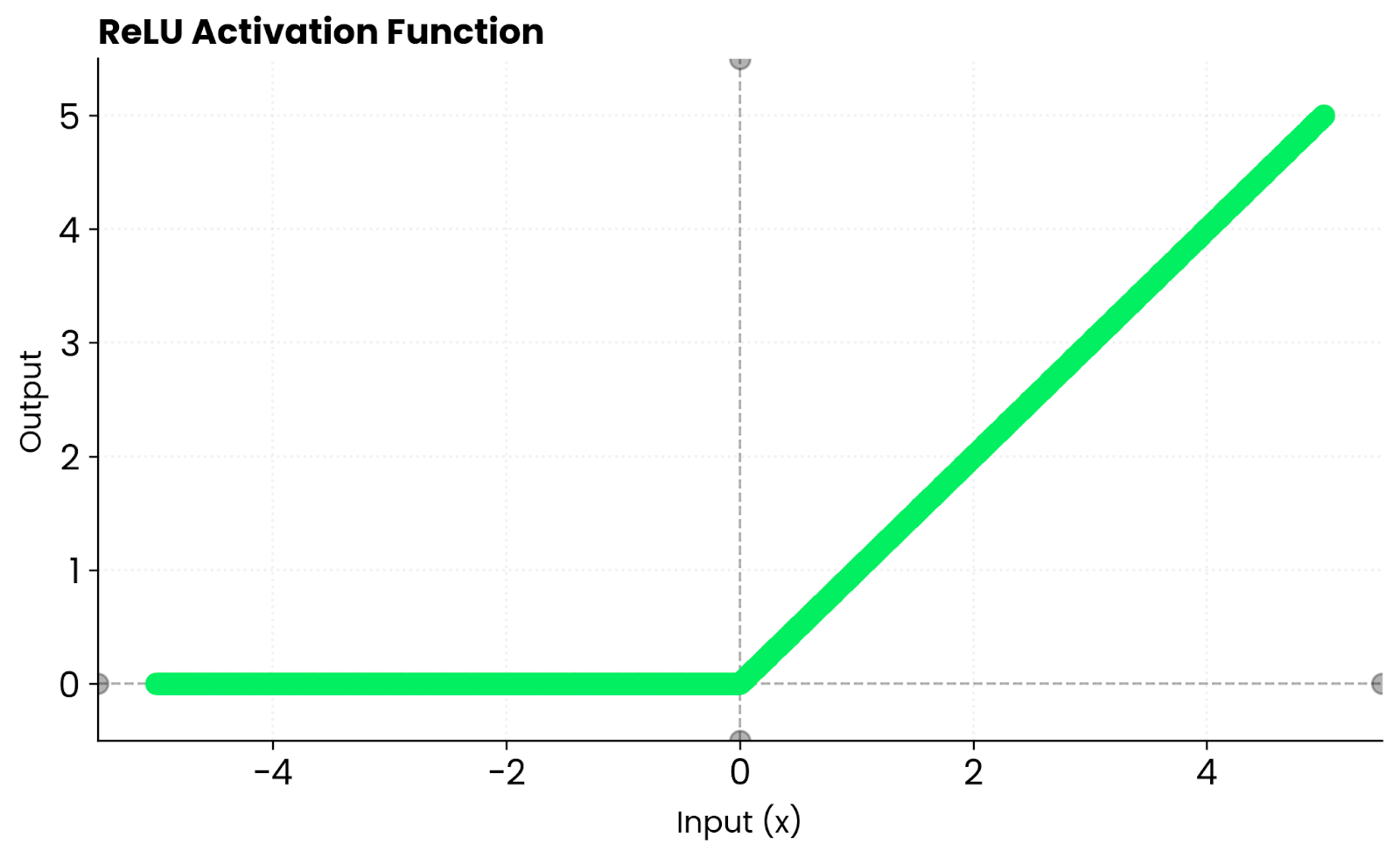
Função ReLU. Imagem do autor

O Softsign parece com o tanh. Ambas são curvas suaves em forma de S. Mas tanh converge mais rápido perto de zero porque sua inclinação é mais acentuada. Isso significa gradientes mais fortes durante as fases iniciais do treinamento, o que pode ajudar sua rede a aprender mais rápido antes que as entradas comecem a atingir as zonas de saturação.

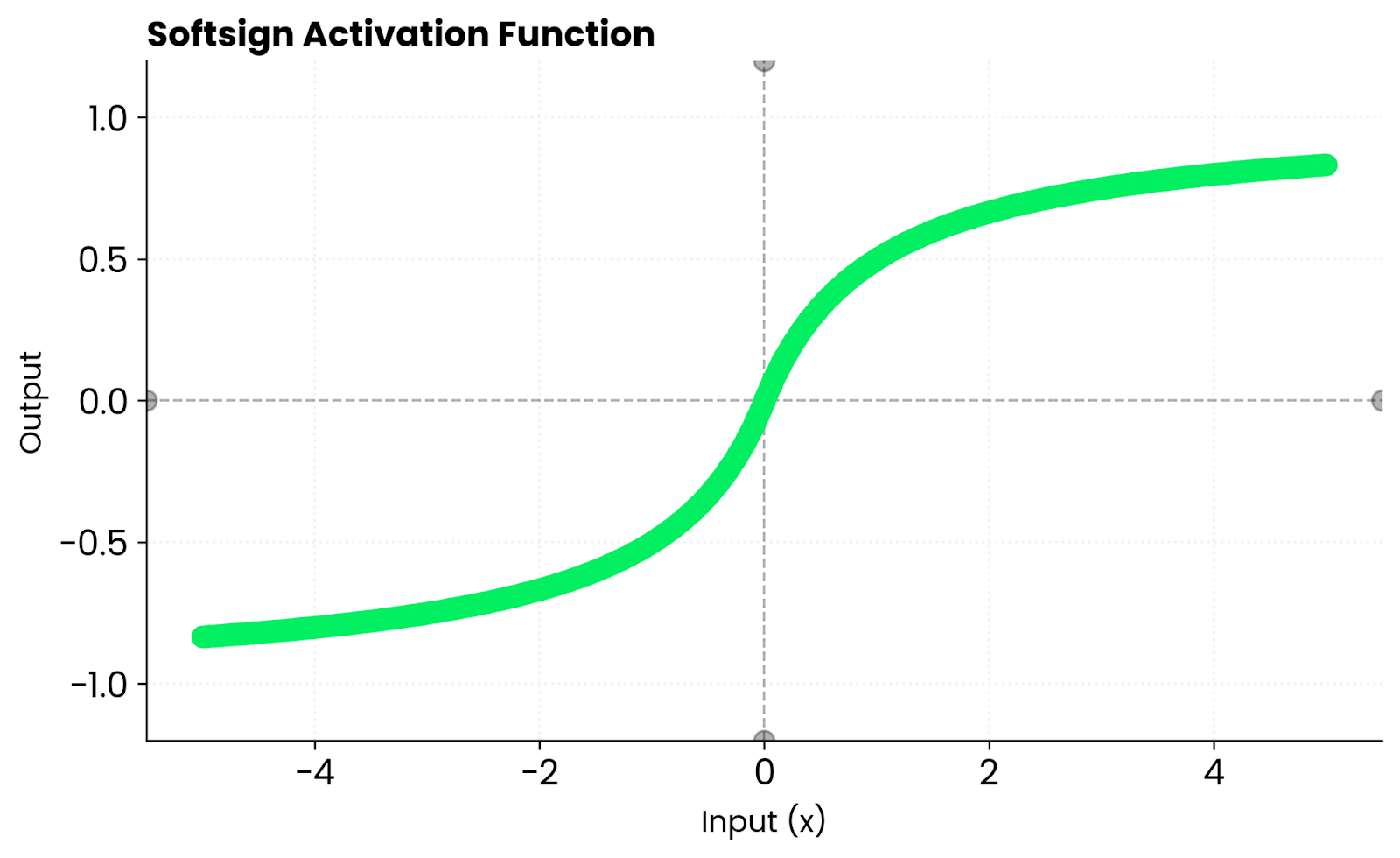
Função Softsign. Imagem do autor

Estou apenas arranhando a superfície com essas funções de ativação. Se você está interessado em alternativas para Tanh e ReLU, leia nosso guia detalhado “s to Softmax and Softplus”(Alternativas para Tanh e ReLU: Softmax e Softplus).

Vantagens do Tanh

Se você está pensando em experimentar o Tanh, aqui estão algumas vantagens a considerar que podem lhe proporcionar um modelo mais preciso no final.

Saída centrada em zero

O Tanh dá resultados equilibrados em torno de zero.

Isso diminui o viés nas atualizações de peso. Quando suas ativações ficam em torno de zero, em vez de serem positivas como a sigmoide, os gradientes não puxam os pesos mais para um lado do que para o outro. Tudo isso resulta em uma convergência mais rápida e um treinamento mais estável.

Gradientes mais fortes perto de zero

O Tanh tem uma inclinação bem íngreme perto de zero.

Isso significa gradientes mais fortes durante a retropropagação em comparação com a sigmoide. Sua rede aprende mais rápido nas primeiras etapas do treinamento, quando a maioria das ativações fica perto de zero. Por outro lado, a inclinação mais suave da Sigmoid faz com que essas atualizações iniciais sejam mais fracas e lentas.

Fluxo gradiente suave

Os derivados de Tanh são contínuos em todos os lugares.

Não tem saltos bruscos nem coisas meio estranhas. Isso te dá uma otimização mais estável em comparação com funções por partes, como ReLU, onde a derivada muda abruptamente de 0 para 1 no zero. Gradientes suaves significam atualizações de peso previsíveis durante todo o treinamento.

Ótimo para redes recorrentes

RNNs, LSTMs e GRUs usam a função tanh nas suas camadas ocultas.

Essas arquiteturas precisam manter estados internos estáveis ao longo dos intervalos de tempo. O Tanh deixa os sinais positivos e negativos passarem, mas mantém os valores dentro de um limite. Esse equilíbrio evita ativações explosivas e ajuda a rede a lembrar informações em sequências mais longas.

Limitações e Compromissos

Antes de mergulhar no código, vou falar sobre algumas áreas em que o Tanh pode não ser tão bom.

Gradientes de desaparecimento

Quando as entradas se afastam muito de zero, os gradientes se aproximam de zero.

Isso acontece porque a função tanh fica saturada em -1 e 1. Quando suas ativações atingem esses extremos, a derivada fica bem pequena e as atualizações de peso ficam bem lentas. Em redes muito profundas, esse problema se agrava porque os gradientes diminuem à medida que se propagam por cada camada até que o aprendizado praticamente pare.

Treino mais lento

O Tanh não cria dispersão.

Cada neurônio fica ativo até certo ponto, diferente do ReLU, onde entradas negativas não produzem saída. Isso quer dizer que sua rede processa mais informações por passagem, o que parece bom, mas na verdade deixa tudo mais lento. A dispersão da ReLU torna o treinamento mais rápido, pois os neurônios inativos ignoram completamente o cálculo.

Menos otimização de hardware

As estruturas modernas e os aceleradores de hardware favorecem o ReLU.

As operações Tanh envolvem exponenciais, que são mais caras de calcular do que a operação simples max(0, x) da ReLU. Os kernels da GPU e os chips de IA especializados são otimizados para ReLU porque ele se tornou o padrão na maioria das arquiteturas. Isso quer dizer que o tanh vai funcionar mais devagar no mesmo hardware, mesmo com arquiteturas de rede iguais.

Tanh no PyTorch

O PyTorch já vem com uma implementação da função Tanh, então você não precisa escrever do zero.

Veja como usá-la como função de ativação em uma rede neural simples:

import torch
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(10, 20),
    nn.Tanh(),
    nn.Linear(20, 1)
)

x = torch.randn(5, 10)
output = model(x)
print(output)

tensor([[ 0.0910],
               [-0.0994],
               [-0.0583],  
               [-0.2177],
               [-0.2546]], grad_fn=<AddmmBackward0>)

Você também pode aplicar tanh diretamente aos tensores:

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = torch.tanh(x)
print(output)

tensor([-0.9640, -0.7616, 0.0000, 0.7616, 0.9640])

Observe como os resultados são simétricos em torno de zero — entradas negativas produzem resultados negativos, e a função trata ambos os lados de forma igual. Essa distribuição equilibrada mantém sua rede estável durante o treinamento e evita a mudança de viés que você veria com funções como sigmoid.

Quando usar o Tanh

Escolha a função Tanh quando seu modelo se beneficiar de ativações centralizadas ou quando estiver trabalhando com redes menores ou recorrentes.

É especialmente eficaz quando:

• Você está treinando RNNs ou LSTMs que precisam de ativações equilibradas. Essas arquiteturas dependem do Tanh para manter estados internos suaves ao longo dos intervalos de tempo, permitindo que sinais positivos e negativos fluam.
• Você está modelando alvos contínuos ou suaves. O fluxo gradiente suave de Tanh funciona bem quando suas saídas precisam ser contínuas e limitadas, como prever valores que naturalmente caem dentro de um intervalo.
• Você quer gradientes estáveis e diferenciáveis, mas não precisa da dispersão do ReLU. Se a sua rede não for profunda o suficiente para aproveitar a vantagem de velocidade do ReLU, o Tanh oferece um comportamento de treinamento mais previsível.

Pelo contrário, evite Tanh em arquiteturas muito profundas, onde gradientes de desaparecimento são uma preocupação. ReLU ou GELU são mais adequados nesse caso porque não ficam saturados para valores positivos.

Conclusão

Resumindo, a função Tanh fica entre a simplicidade da Sigmoid e a velocidade da ReLU.

É suave, simétrico e ainda relevante no aprendizado profundo, especialmente onde as ativações equilibradas são o que mais importa. Você não vai encontrar isso em toda arquitetura moderna, mas tem seu lugar quando você precisa de saídas centralizadas e fluxo de gradiente estável.

Se você não tem certeza se deve usar o Tanh ou não, basta seguir estas orientações:

• Use ReLU para redes grandes e profundas. É mais rápido, funciona bem com hardware moderno e evita gradientes desaparecidos para valores positivos.
• Use Tanh quando precisar de estabilidade, simetria e um fluxo de gradiente mais suave. Isso significa redes recorrentes, arquiteturas menores e casos em que ativações centradas em zero melhoram a convergência.

Faça experimentos, compare os resultados e deixe seus dados decidirem qual ativação é mais adequada para sua tarefa. Quer saber mais? Inscreva-se no nosso programa de Machine Learning Scientist em Python para entender os detalhes do aprendizado supervisionado, não supervisionado e profundo.