Curso
Introdução ao aprendizado de máquina
2 h
260.6K
A ReLU tem sido a função de ativação padrão no aprendizado profundo há anos. E tem um bom motivo pra isso: é simples e funciona bem na maioria dos casos. Mas quando os neurônios começam a produzir zero durante o treinamento, eles param de aprender, seus gradientes se tornam zero e a retropropagação não consegue atualizar seus pesos. Em redes mais profundas, esse problema pode afetar vários neurônios e diminuir a capacidade do seu modelo de capturar padrões nos seus dados.
Em linguagem simples: sua rede para de aprender.
A Softplus oferece uma alternativa suave e diferenciada que resolve esse problema, mantendo a maioria dos benefícios da ReLU. Ele se aproxima do comportamento do ReLU para entradas positivas, mas fornece gradientes diferentes de zero para valores negativos. Isso mantém os neurônios ativos durante todo o treinamento.
Neste artigo, você vai aprender o que é Softplus, como ele se compara matematicamente ao ReLU e quando você deve escolhê-lo em vez de outras funções de ativação.
Se você é completamente novo no aprendizado profundo, confira nosso guia detalhado sobre funções de ativação em redes neurais.
O que é a função Softplus?
Softplus é uma função de ativação suave que funciona como uma aproximação diferenciável da ReLU.
A função pega qualquer número real como entrada e mostra um valor positivo. O Softplus não tem um canto acentuado em zero como o ReLU. Ele faz uma curva suave nesse ponto de transição.
Aqui está a definição matemática:
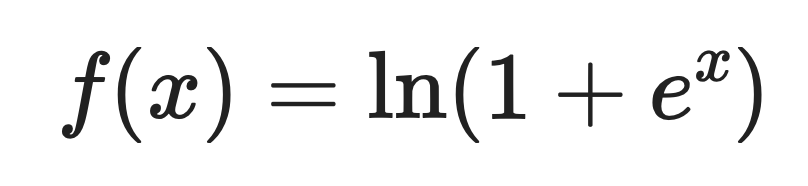
Onde:
- x é o valor de entrada
- e é o número de Euler (mais ou menos 2,718)
- ln é o logaritmo natural
Para entradas positivas grandes, o Softplus retorna valores próximos à própria entrada. Para entradas negativas, ele retorna pequenos valores positivos em vez de zero.
Derivado da Softplus
A derivada da Softplus é a função logística sigmoidal. sigmoide logística.
Isso quer dizer:
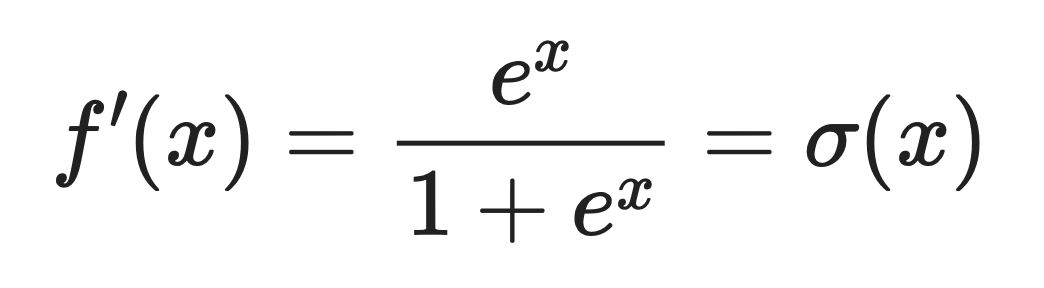
Onde σ(x) é a função sigmoide que você provavelmente já viu antes.
Essa propriedade derivada torna o Softplus útil quando você precisa de um fluxo de gradiente suave durante a retropropagação. Os gradientes nunca caem para zero. Isso quer dizer que os neurônios podem sempre atualizar seus pesos e continuar aprendendo.
Comportamento em situações extremas
O Softplus age de forma diferente dependendo se a entrada é grande e positiva ou grande e negativa.
Para valores positivos grandes:
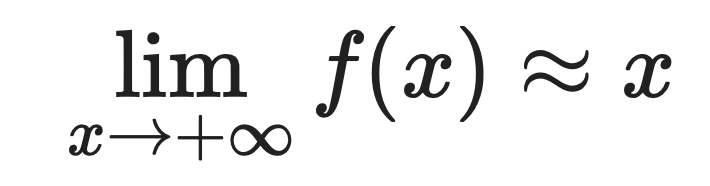
Para valores negativos grandes:
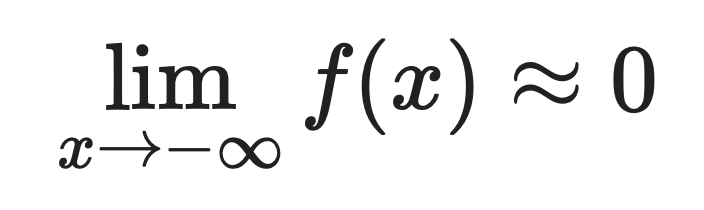
É por isso que o Softplus se aproxima tão bem do ReLU. Quando x é positivo e grande, as duas funções devolvem aproximadamente o mesmo valor.
A diferença é visível nas entradas negativas. A ReLU dá exatamente zero para entradas negativas, e a Softplus dá pequenos valores positivos.
Essa pequena diferença evita o problema da morte dos neurônios. Os neurônios que usam Softplus podem se recuperar de ativações negativas porque seus gradientes nunca desaparecem completamente.
Propriedades matemáticas e computacionais
O Softplus tem propriedades matemáticas que você precisa conhecer. Eles fazem disso mais do que só uma versão suave do ReLU.
Suavidade e diferenciabilidade
O Softplus é infinitamente diferenciável em todos os pontos.
Isso quer dizer que você pode derivar quantas vezes quiser, e a função continua suave. Em termos matemáticos, é uma função analítica.
Já a ReLU tem uma dobra no zero — um canto bem acentuado onde a derivada não existe. Esse ponto não diferenciável pode causar problemas em algoritmos de otimização que assumem gradientes suaves.
No aprendizado profundo, a otimização suave funciona melhor quando a superfície de perda é suave. Se você estiver usando métodos de otimização de segunda ordem ou qualquer algoritmo que dependa de transições suaves de gradiente, o Softplus oferece essa suavidade.
Estabilidade numérica
Calcular exponenciais pode causar problemas de estouro quando as entradas ficam grandes.
As estruturas de deep learning lidam com isso usando um parâmetro chamado “ threshold ”. Quando a entrada passa desse limite, a função deixa de calcular o logaritmo e passa a devolver uma saída linear.
Funciona assim:
- Para entradas pequenas: calcule o Softplus diretamente
- Para entradas grandes além do limite: devolva as entradas diretamente
Isso evita o estouro numérico, mantendo o comportamento que você precisa. Para grandes entradas positivas, o Softplus aproxima-se de uma função linear de qualquer maneira, então a mudança não afeta significativamente a saída.
Relação com outras funções
O Softplus conecta-se a algumas outras funções de ativação e probabilidade. Veja como:
-
e sigmoide: Como você viu antes, a derivada da Softplus é a função sigmoide. Isso quer dizer que Softplus é a integral da sigmoide, o que faz sentido quando você pensa nas formas delas.
-
LogSumExp: Softplus é, na verdade, um caso especial da função LogSumExp. Para duas entradas,
LogSumExp(0, x) = ln(1 + e^x) = Softplus(x). Isso conecta o Softplus às técnicas de estabilidade numérica usadas no machine learning. -
Softmax: LogSumExp é a base do Softmax, então o Softplus também vem dessa linhagem. Ambas as funções usam o truque log-exp para estabilidade numérica.
-
Função logit: O logit é o inverso do sigmoide. Como a sigmoide é a derivada da Softplus, essas três funções formam uma família conectada na teoria da probabilidade.
-
Conjugado convexo: Na análise convexa, o conjugado convexo de Softplus é a entropia binária negativa. Isso conecta o Softplus aos princípios de maximização da entropia usados na teoria da informação e na modelagem probabilística.
Se você está trabalhando com modelos probabilísticos ou estruturas bayesianas, essa conexão com a entropia faz do Softplus uma escolha natural para garantir que suas ativações estejam alinhadas com os princípios de entropia máxima.
Vantagens de usar o Softplus
O Softplus resolve problemas específicos que o ReLU não consegue lidar bem. Aqui estão quatro deles.
Suave e diferenciável
O Softplus é suave em todos os pontos da curva.
Isso quer dizer que os gradientes fluem sem parar durante a retropropagação, sem picos ou interrupções. Quando você está treinando uma rede, um fluxo de gradiente suave leva a atualizações de peso mais estáveis e um melhor comportamento de convergência.
O canto acentuado da ReLU em zero pode causar descontinuidades no gradiente. A Softplus não tem esse problema.
Impede a morte dos neurônios
O Softplus nunca mostra exatamente zero, mesmo com entradas negativas grandes.
Isso quer dizer que cada neurônio pode continuar aprendendo porque os gradientes nunca desaparecem completamente. Com o ReLU, um neurônio que começa a produzir zero pode ficar preso lá para sempre — seu gradiente é zero, então as atualizações de peso não o movem.
A Softplus te dá uma rede de segurança. Os neurônios podem se recuperar de ativações negativas e começar a contribuir para a rede novamente.
A saída é sempre positiva
O Softplus garante resultados não negativos para qualquer entrada.
Isso é importante quando você está criando modelos que precisam de previsões positivas. A regressão de Poisson modelam dados de contagem (clientes, eventos, cliques) onde valores negativos não fazem sentido. Os modelos generativos geralmente precisam de resultados positivos para mostrar probabilidades ou intensidades.
Mais adequado para certas tarefas
Algumas tarefas se beneficiam de um comportamento de ativação suave e contínuo.
Tarefas de regressão com funções-alvo suaves funcionam melhor com ativações suaves. Se você está prevendo valores contínuos, como temperatura, preço ou distância, o Softplus se alinha melhor com a suavidade subjacente dos seus dados.
Modelos bayesianos e estruturas probabilísticas também preferem funções suaves. Quando você está modelando incertezas ou trabalhando com distribuições de probabilidade, as derivadas contínuas do Softplus tornam as operações matemáticas mais claras e estáveis.
Se você trabalha nessas áreas, o Softplus oferece melhores garantias teóricas e resultados práticos do que as transições bruscas do ReLU.
Limitações e Compromissos
Tem algumas limitações que você precisa saber sobre o Softplus antes de abandonar o ReLU de vez. Aqui estão três deles.
Maior custo computacional
A ReLU usa uma operação máxima simples: max(0, x).
O Softplus calcula exponenciais e logaritmos: ln(1 + e^x). Essas operações são mais lentas, principalmente quando você as executa milhões de vezes em grandes redes com milhares de neurônios.
A diferença faz diferença. Essa sobrecarga computacional pode aumentar o tempo de treinamento.
Convergência mais lenta
O Softplus tem gradientes mais suaves, o que parece bom no papel.
Mas suave nem sempre quer dizer rápido. As transições bruscas da ReLU criam ativações esparsas — muitos neurônios produzem exatamente zero. Essa dispersão ajuda os gradientes a se espalharem mais rápido pela rede durante a retropropagação.
O Softplus não tem essa escassez. Cada neurônio gera um valor diferente de zero, o que significa mais cálculos e, potencialmente, uma convergência mais lenta em arquiteturas profundas.
Menos comum na prática
A ReLU tem dominado o aprendizado profundo há anos.
Isso quer dizer que tem mais documentação, problemas/soluções e recursos gerais sobre o assunto. A Softplus não recebe o mesmo tratamento. Menos gente usa, então tem menos conhecimento da comunidade, menos respostas no Stack Overflow e menos modelos pré-treinados usando isso.
Quando você escolhe o Softplus, tá optando por um caminho com menos suporte e, talvez, mais depuração por conta própria.
Softplus in PyTorch
O PyTorch facilita o uso do Softplus com suporte integrado e dois parâmetros que controlam seu comportamento.
Só pra você saber, essa é a versão do PyTorch que estou usando:
import torch
import torch.nn as nn
print(torch.__version__)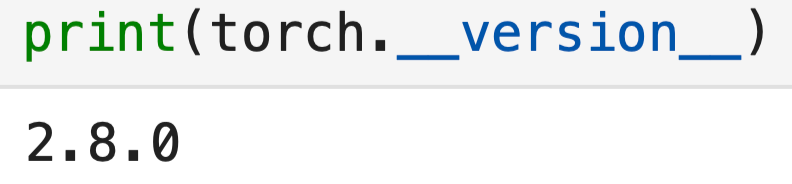
Aqui está a implementação básica:
# Create a Softplus activation function
softplus = nn.Softplus(beta=1, threshold=20)
# Apply it to some input
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = softplus(x)
print(output)
Simples assim. Mas esses dois parâmetros - beta e threshold - mudam como a função funciona. Vamos dar uma olhada neles com mais detalhes.
O parâmetro beta
O parâmetro “ beta ” controla a suavidade da curva Softplus.
Quando você aumenta beta, a função fica mais íngreme e mais parecida com ReLU. Quando você diminui, a função fica mais suave e gradual. Veja como funciona no código:
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
# Steeper activation (closer to ReLU)
softplus_steep = nn.Softplus(beta=2, threshold=20)
output_steep = softplus_steep(x)
# Smoother activation
softplus_smooth = nn.Softplus(beta=0.5, threshold=20)
output_smooth = softplus_smooth(x)
print("Softplus - Steeper activation")
print(output_steep)
print()
print("Softplus - Smoother activation")
print(output_smooth)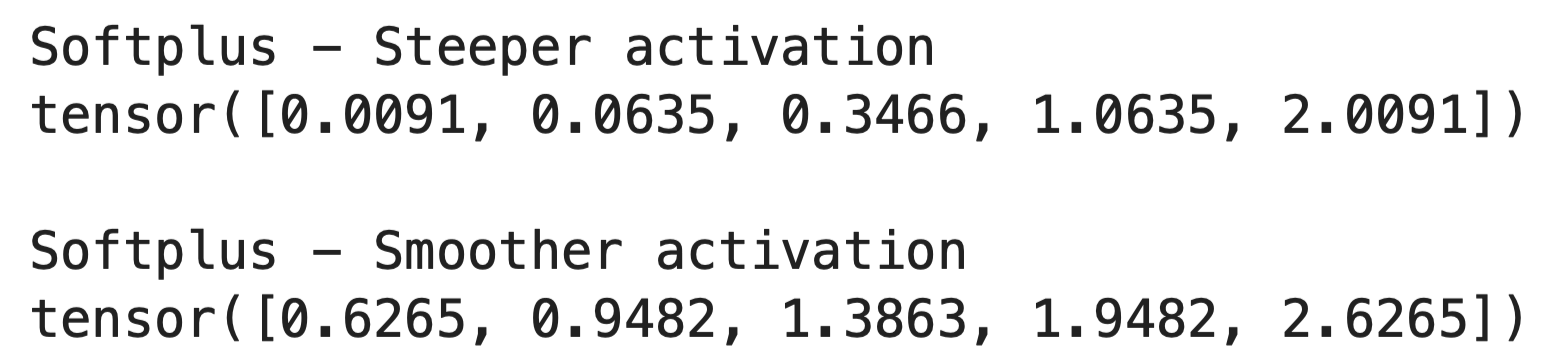
O padrão beta=1 funciona bem na maioria dos casos. Você só mudaria isso se precisasse ajustar a sensibilidade da ativação para tarefas específicas.
O parâmetro limite
O parâmetro ` threshold ` evita o estouro numérico para entradas grandes.
Lembra como o cálculo de e^x pode explodir para valores grandes de x? Quando a entrada passa do limite, o PyTorch deixa de calcular a fórmula Softplus completa e passa a só devolver a entrada diretamente:
softplus = nn.Softplus(beta=1, threshold=20)
# Large input bypasses the exponential
large_input = torch.tensor([25.0])
print(softplus(large_input))
O padrão threshold=20 funciona na maioria dos casos. Neste ponto, o Softplus já se aproxima de uma função linear, então a mudança não afeta os resultados.
Quando usar o Softplus
Escolha Softplus quando precisar de suavidade de gradiente e e para otimização. Se você estiver usando métodos de otimização de segunda ordem ou algoritmos que assumem superfícies de perda suaves, o Softplus fornece as derivadas contínuas nas quais esses métodos se baseiam.
Use isso quando seu modelo precisar de resultados não negativos. Os dados de contagem, os valores de intensidade e os parâmetros de probabilidade precisam permanecer positivos. O Softplus lida com isso naturalmente, sem restrições adicionais.
As redes superficiais aproveitam mais o Softplus do que as profundas. Quando você tem só algumas camadas, perder até mesmo um neurônio por causa do problema do ReLU moribundo prejudica o desempenho. O Softplus mantém todos os neurônios ativos e aprendendo.
Você também pode escolher o Softplus para modelos probabilísticos e estruturas bayesianas. Os gradientes suaves e as conexões de entropia tornam as operações matemáticas mais claras. Os modelos baseados em energia também se beneficiam da natureza contínua da Softplus.
Modelos em que você precisa interpretar gradientes contínuos funcionam melhor com o Softplus. Se você está analisando como sua rede responde a mudanças de entrada ou estudando o fluxo gradiente, as derivadas suaves oferecem insights mais claros do que as transições bruscas da ReLU.
Quando o ReLU ainda é melhor
Não mude para o Softplus só porque parece melhor no papel ou porque é uma novidade brilhante.
- Redes grandes e profundas treinam mais rápido com ReLU. A sobrecarga computacional do Softplus se acumula em centenas de camadas e milhões de parâmetros. A escassez do ReLU também ajuda com a memória e a velocidade.
- Os sistemas de produção geralmente preferem o ReLU porque as otimizações de hardware são feitas especialmente para ele. Seu treinamento pode ficar 10-20% mais lento com o Softplus no mesmo hardware.
- Tarefas padrão de visão computacional e NLP geralmente não se beneficiam do Softplus. A galera passou anos otimizando arquiteturas em torno do ReLU, e mudar as funções de ativação significa reconstruir todo esse conhecimento.
Comece com ReLU para a maioria dos projetos. Mude para o Softplus só quando você tiver problemas específicos que as propriedades dele resolvem.
Conclusão
Resumindo, o Softplus oferece uma alternativa suave ao ReLU quando você precisar.
Não vai substituir a ReLU como função de ativação padrão — e nem precisa. O Softplus resolve problemas específicos: neurônios morrendo em redes rasas, modelos que precisam de resultados não negativos e tarefas onde o fluxo suave do gradiente é importante para a otimização.
Você obtém melhores propriedades matemáticas em detrimento da velocidade computacional. Na maioria dos projetos de deep learning, a simplicidade e a velocidade do ReLU são os pontos fortes. Mas quando você está trabalhando com modelos probabilísticos, estruturas bayesianas ou tarefas de regressão com funções-alvo suaves, o Softplus se torna a melhor escolha.
Teste os dois. Faça experimentos. Deixa o teu problema específico guiar a decisão.
Quer saber mais? Dá uma olhada nos nossos recursos incríveis:
