Función Tanh: Por qué los resultados centrados en cero son importantes para las redes neuronales

¿Tu red neuronal se ha estancado en un 60 % de precisión y no sabes por qué?

Has ajustado la tasa de aprendizaje, añadido más capas y jugado con el tamaño del lote. Nada funciona. La pérdida de entrenamiento apenas varía después de las primeras épocas. Empiezas a cuestionar toda tu configuración. Quizás los datos sean incorrectos, quizás la arquitectura sea errónea. Pero lo que realmente está sucediendo es que tu función de activación está empujando todas las salidas en una sola dirección, lo que hace imposible que la red aprenda patrones equilibrados.

Tanh (tangente hiperbólica) resuelve esto centrando los resultados alrededor de cero, en un rango de -1 a 1. Esto ayuda a que tus modelos converjan más rápidamente y mantiene los gradientes fluyendo simétricamente durante la retropropagación.

En este artículo, aprenderás qué es tanh, cómo funciona matemáticamente, cuándo utilizarlo en lugar de ReLU o sigmoid, y cómo implementarlo en PyTorch. Si eres nuevo en el aprendizaje profundo, consulta nuestra guía detallada sobre las funciones de activación en las redes neuronales.

¿Qué es la función tanh?

La función tanh asigna cualquier entrada a un valor entre -1 y 1.

Es una curva suave en forma de S definida por esta fórmula:

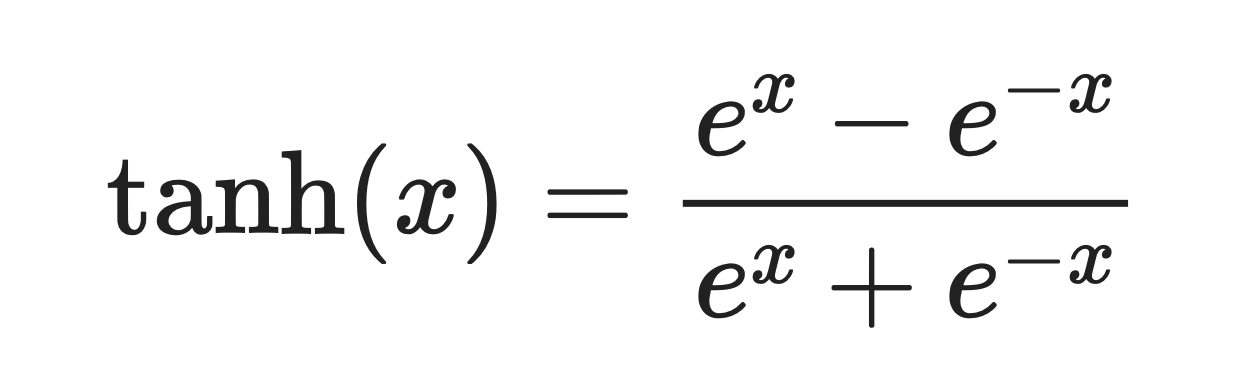
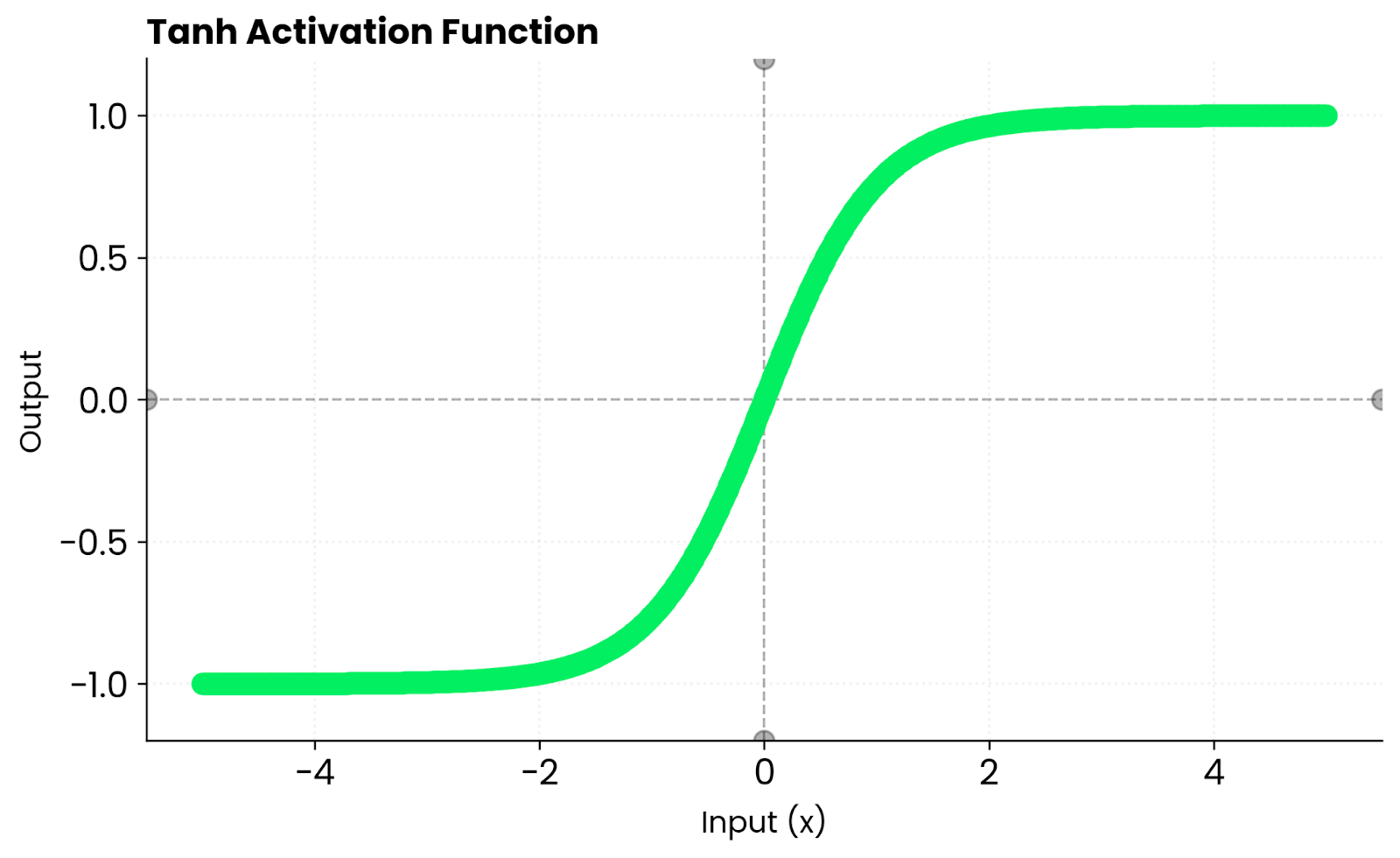
Función tanh. Imagen del autor

La función se comporta de manera predecible en situaciones extremas. Cuando le asignas un número positivo grande, el resultado es cercano a 1. Para un número negativo grande, obtendrás un resultado cercano a -1.

Alrededor de cero, tanh se comporta de forma casi lineal. Esto significa que los gradientes fluyen suavemente durante la retropropagación, en lugar de aplastarse o distorsionarse.

A modo de comparación, la sigmoide solo genera valores positivos entre 0 y 1. Tanh genera números tanto positivos como negativos. Mantiene las activaciones equilibradas en torno a cero, lo que ayuda a que la optimización converja más rápidamente en muchas arquitecturas de red.

Verás que tanh se utiliza con mayor frecuencia en redes recurrentes y en cualquier lugar donde las activaciones centradas mejoren la estabilidad.

Propiedades matemáticas y computacionales

Tanh tiene algunas propiedades matemáticas que todo aspirante a ingeniero de machine learning debe conocer.

Suave y diferenciable

Tanh es infinitamente diferenciable y suave en todas partes.

Esto es importante para la optimización basada en gradientes. No te encontrarás con esquinas pronunciadas como ocurre con ReLU, donde la derivada salta de 0 a 1 instantáneamente. Los gradientes suaves permiten actualizaciones de peso más predecibles durante la retropropagación.

Salida centrada en cero

La sigmoide genera valores entre 0 y 1. Tanh genera valores entre -1 y 1.

Cuando las activaciones se mantienen equilibradas en torno a cero, tu red converge más rápidamente. Las actualizaciones de peso no se sesgan en una dirección y los gradientes fluyen de manera más uniforme a través de las capas.

Limitado y estable

El rango de salida de Tanh está fijado entre -1 y 1.

Estos límites evitan la inestabilidad numérica. Si trabajas con redes que no pueden manejar activaciones explosivas, tanh mantiene todo bajo control sin recortes ni manejos especiales.

Comportamiento en situaciones extremas

Para valores positivos grandes, tanh se aproxima a 1. Para valores negativos grandes, se aproxima a -1.

Esta simetría mantiene las activaciones centradas y evita el desplazamiento del sesgo que se observa en funciones no centradas en cero, como la sigmoide. En las redes profundas, esa propiedad ayuda a que las actualizaciones de peso se propaguen de manera más uniforme a través de las capas: la red no desarrolla una preferencia por los valores positivos o negativos.

Derivada de tanh

La derivada de tanh es:

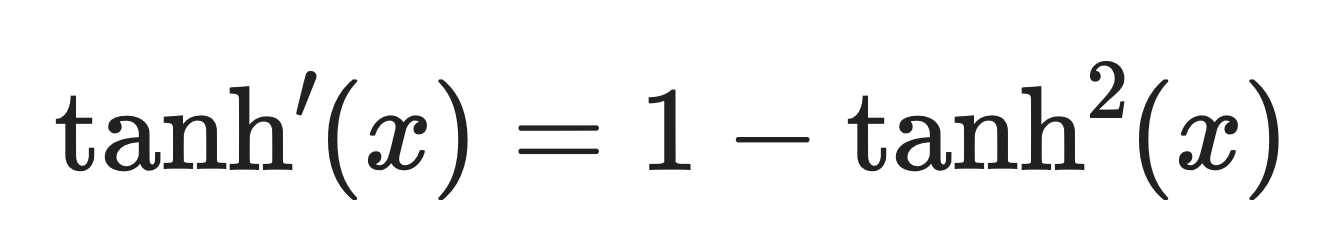
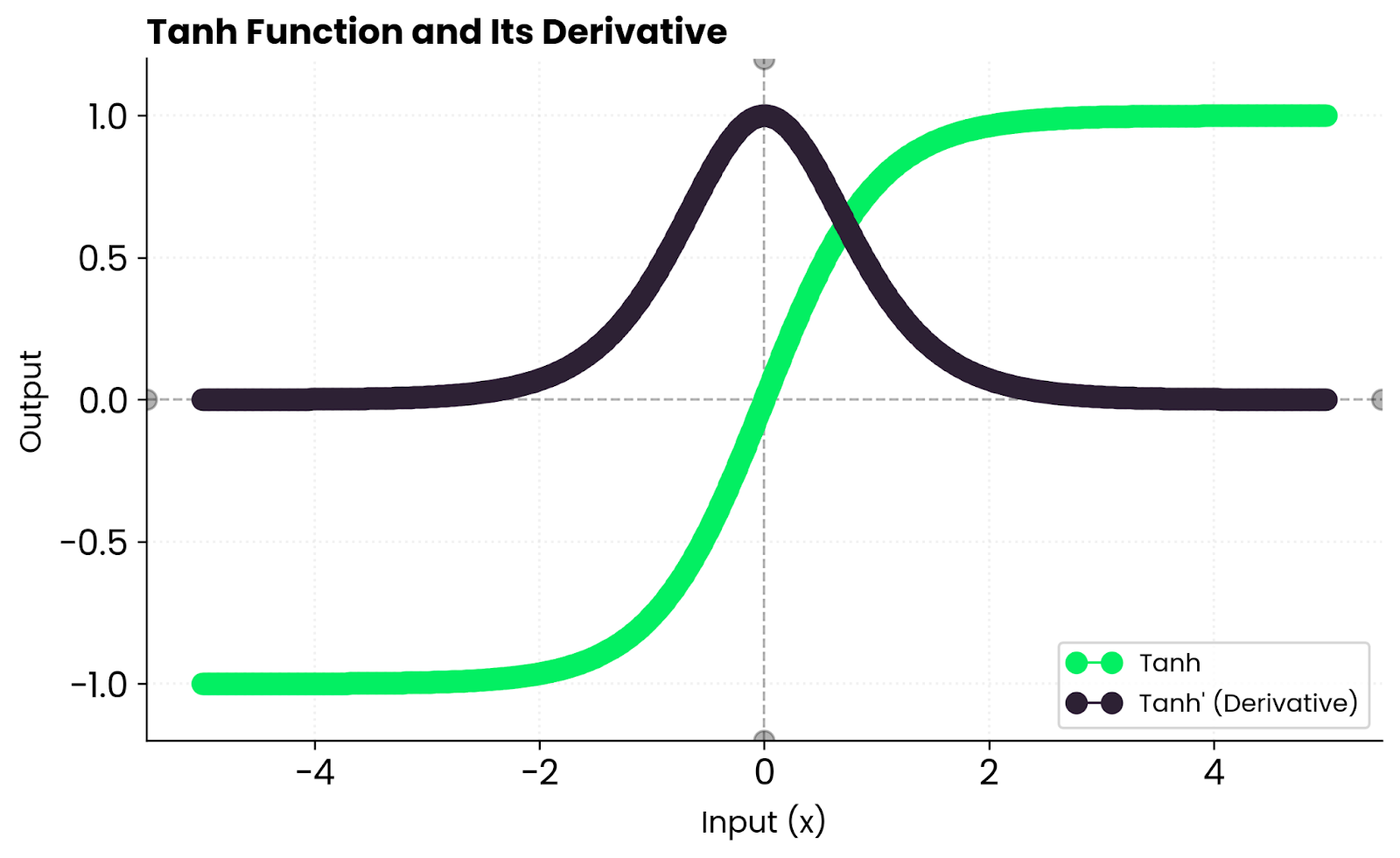
Derivada de Tanh. Imagen del autor.

Esto significa que los gradientes son fuertes cerca de cero, pero se reducen hacia los bordes a medida que la función se satura. Cuando tanh(x) se aproxima a 1 o -1, la derivada se aproxima a cero, lo que ralentiza el aprendizaje de esas neuronas.

En la práctica, se obtiene un aprendizaje estable con entradas moderadas, pero pueden aparecer gradientes que desaparecen cuando las entradas son demasiado grandes o demasiado pequeñas. Por eso las redes profundas suelen preferir ReLU: no se satura con valores positivos.

Tanh contra Otras funciones

Tanh no es la única función de activación que existe, y comprender cómo se compara con otras alternativas te ayudará a elegir la más adecuada para tu red.

Sigmoid es un pariente cercano de tanh. De hecho, tanh es solo una versión escalada y desplazada de sigmoid:

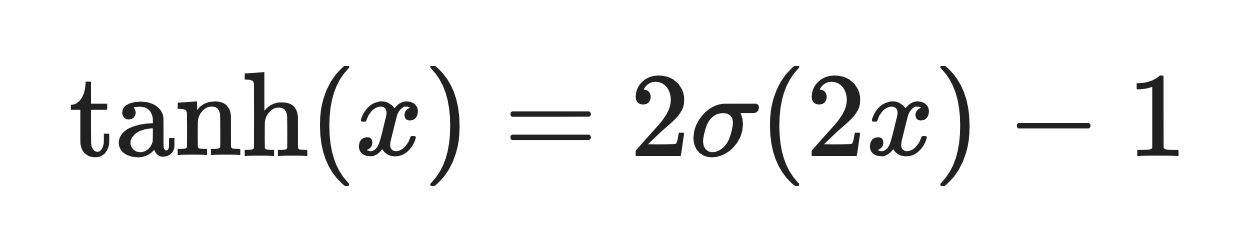
Donde σ(x) es la función sigmoide.

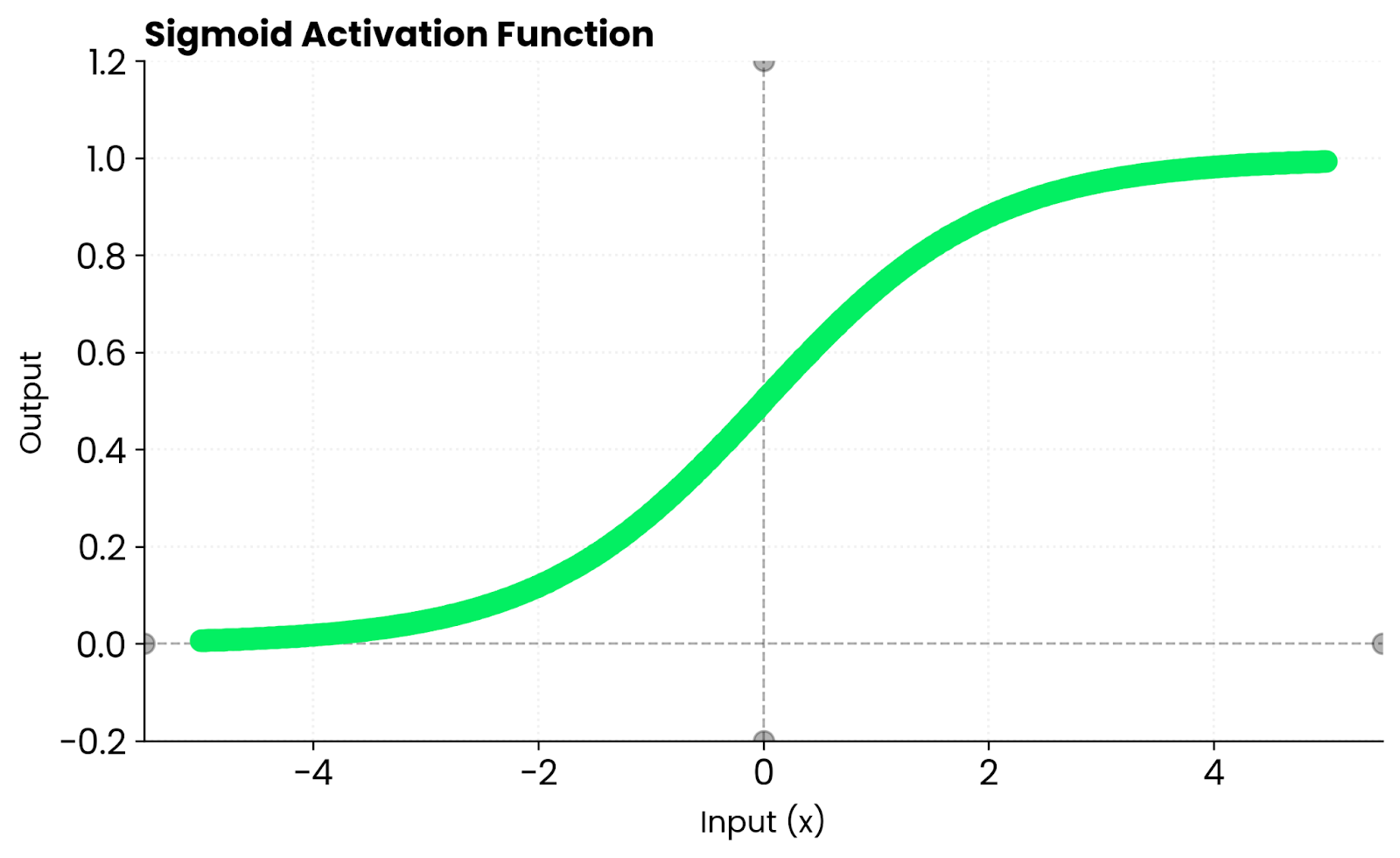
Función sigmoidea. Imagen del autor

La diferencia clave es que Sigmoid genera valores entre 0 y 1, mientras que tanh genera valores entre -1 y 1. Ese centrado en cero hace que tanh converja más rápidamente en la mayoría de los casos.

ReLU adopta un enfoque diferente. Devuelve cero para entradas negativas y pasa las entradas positivas sin cambios. Esto crea dispersión, lo que significa que muchas neuronas permanecen inactivas, lo que acelera el entrenamiento. Pero ReLU elimina los gradientes para los valores negativos. Tanh no tiene este problema porque mantiene gradientes distintos de cero para entradas negativas. Se satura en ambos extremos, lo que puede ralentizar el aprendizaje cuando las entradas son demasiado grandes o demasiado pequeñas.

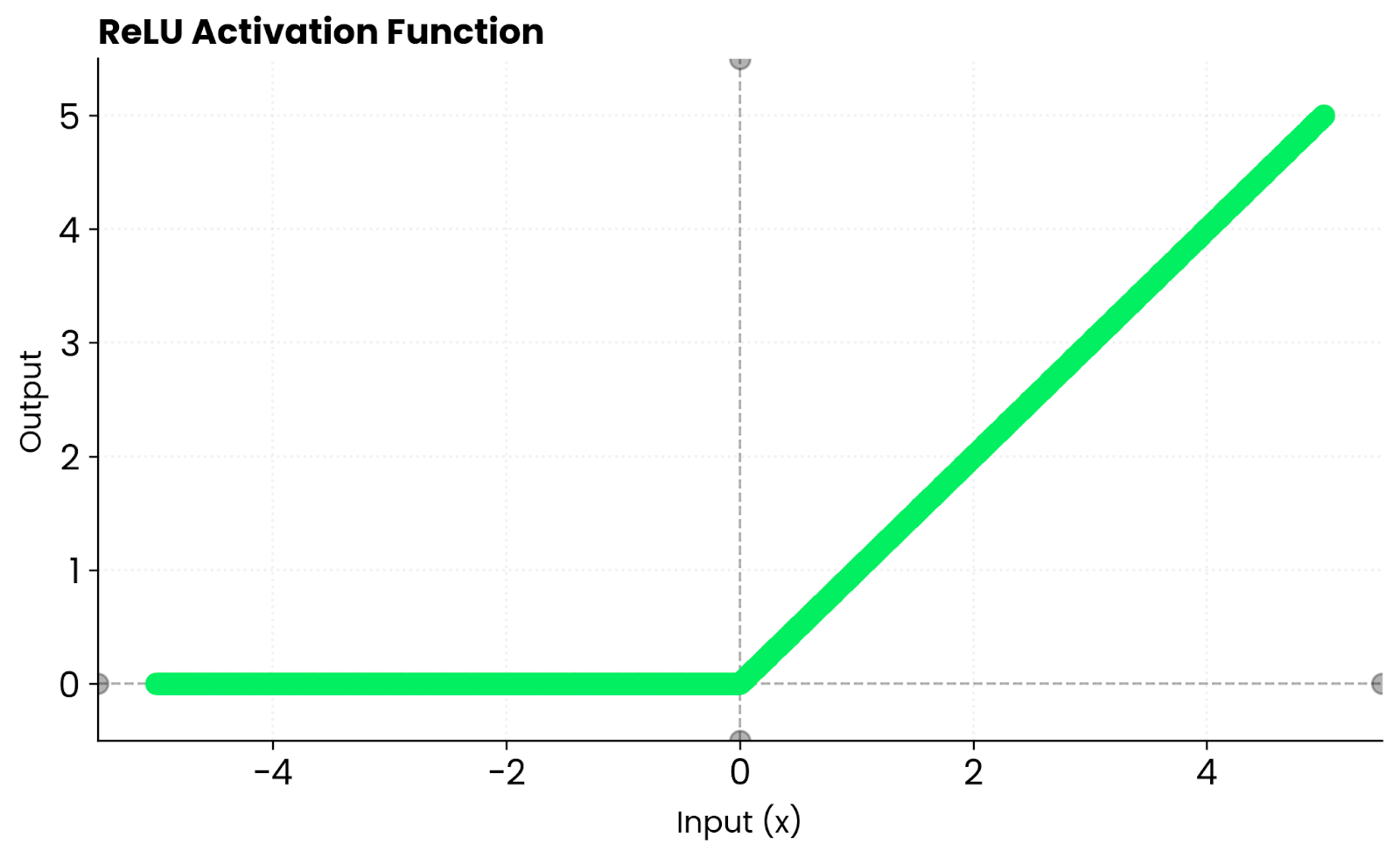
Función ReLU. Imagen del autor

Softsign es similar a tanh. Ambas son curvas suaves en forma de S. Pero tanh converge más rápido cerca de cero porque su pendiente es más pronunciada. Esto significa gradientes más fuertes durante las primeras etapas del entrenamiento, lo que puede ayudar a tu red a aprender más rápido antes de que las entradas comiencen a alcanzar las zonas de saturación.

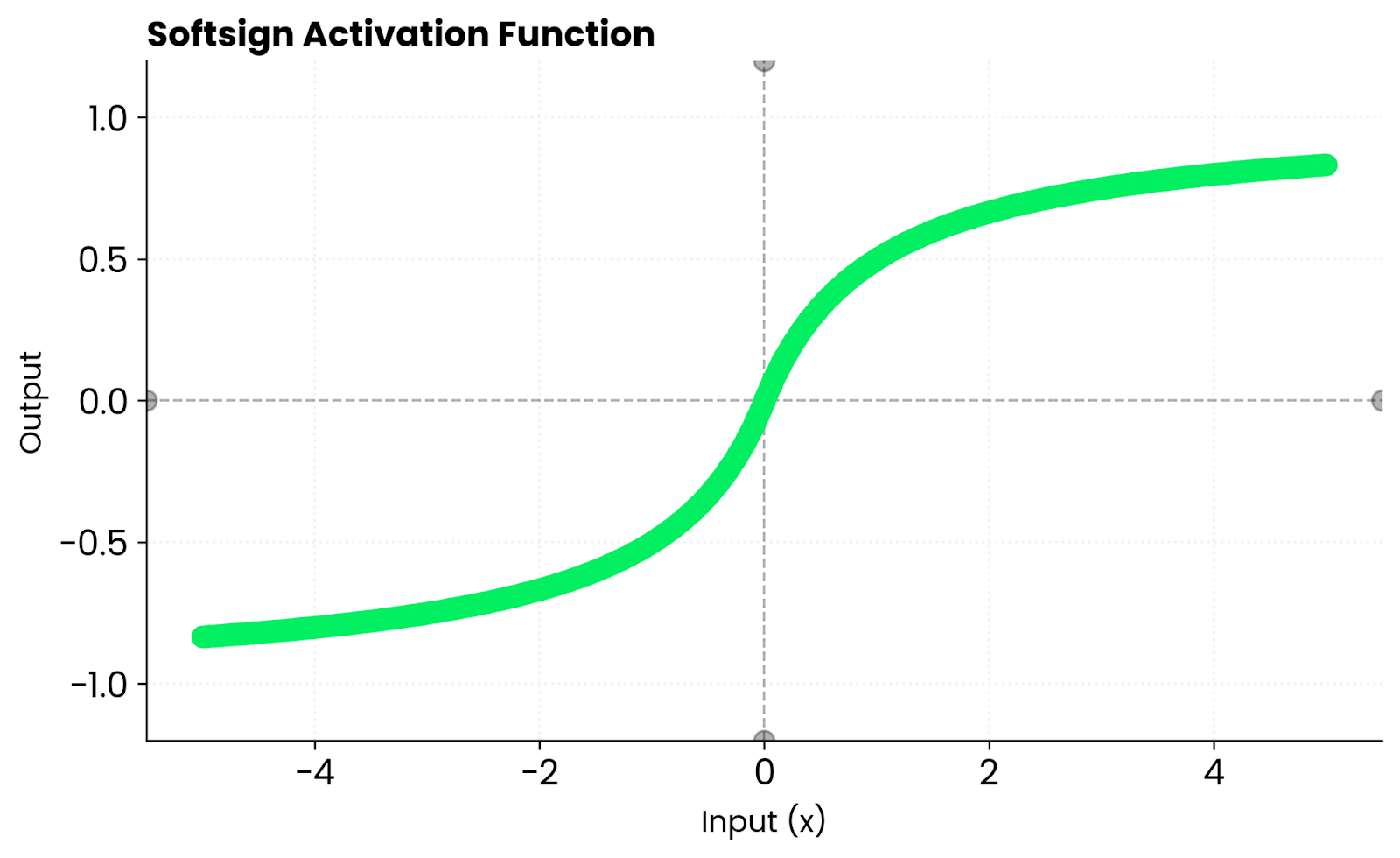
Función Softsign. Imagen del autor

Solo estoy rascando la superficie con estas funciones de activación. Si te interesan las alternativas a Tanh y ReLU, lee nuestra guía detallada «s to Softmax and Softplus»(Alternativas a Tanh y ReLU: una introducción a las funciones activadoras).

Ventajas de Tanh

Si estás decidiendo si vale la pena probar Tanh, aquí tienes algunas ventajas que debes tener en cuenta y que podrían proporcionarte un modelo más preciso al final.

Salida centrada en cero

Tanh produce resultados equilibrados alrededor de cero.

Esto reduce el sesgo en las actualizaciones de peso. Cuando tus activaciones se centran en torno al cero en lugar de estar sesgadas hacia el positivo como en el caso de la sigmoide, los gradientes no tiran de los pesos en una dirección más que en otra. Todo ello se traduce en una convergencia más rápida y un entrenamiento más estable.

Gradientes más fuertes cerca de cero

Tanh tiene una pendiente pronunciada cercana a cero.

Esto significa gradientes más fuertes durante la retropropagación en comparación con la sigmoide. Tu red aprende más rápido en las primeras etapas del entrenamiento, cuando la mayoría de las activaciones se sitúan cerca de cero. Por otro lado, la pendiente más suave de Sigmoid hace que esas actualizaciones iniciales sean más débiles y lentas.

Flujo de gradiente suave

Los derivados de Tanh son continuos en todas partes.

No hay saltos repentinos ni discontinuidades. Esto proporciona una optimización más estable en comparación con funciones por tramos como ReLU, en las que la derivada cambia bruscamente de 0 a 1 en cero. Los gradientes suaves permiten actualizaciones de peso predecibles a lo largo del entrenamiento.

Ideal para redes recurrentes

Las RNN, LSTM y GRU utilizan la función tanh en sus capas ocultas.

Estas arquitecturas deben mantener estados internos fluidos a lo largo de los intervalos de tiempo. Tanh permite que fluyan tanto las señales positivas como las negativas, al tiempo que mantiene los valores dentro de unos límites. Este equilibrio evita activaciones explosivas y ayuda a la red a recordar información durante secuencias más largas.

Limitaciones y compensaciones

Antes de profundizar en el código, voy a abordar un par de aspectos en los que Tanh podría quedarse corto.

Gradientes que desaparecen

Cuando las entradas se alejan de cero, los gradientes se acercan a cero.

Esto ocurre porque tanh se satura en -1 y 1. Una vez que tus activaciones alcanzan estos extremos, la derivada se vuelve minúscula y las actualizaciones de peso se ralentizan hasta casi detenerse. En redes muy profundas, este problema se agrava porque los gradientes se reducen a medida que se retropropagan a través de cada capa hasta que el aprendizaje prácticamente se detiene.

Entrenamiento más lento

Tanh no crea dispersión.

Todas las neuronas permanecen activas en cierta medida, a diferencia de ReLU, donde las entradas negativas producen una salida cero. Esto significa que tu red procesa más información por cada paso hacia adelante, lo que suena bien, pero en realidad ralentiza las cosas. La escasez de ReLU agiliza el entrenamiento, ya que las neuronas inactivas omiten por completo el cálculo.

Menos optimización del hardware

Los marcos modernos y los aceleradores de hardware favorecen a ReLU.

Las operaciones Tanh implican exponenciales, que son más costosas de calcular que la sencilla operación max(0, x) de ReLU. Los núcleos de GPU y los chips de IA especializados están optimizados para ReLU, ya que se ha convertido en el estándar predeterminado en la mayoría de las arquitecturas. Esto significa que tanh funcionará más lentamente en el mismo hardware, incluso con arquitecturas de red idénticas.

Tanh en PyTorch

PyTorch te ofrece de forma nativa una implementación de la función Tanh, lo que significa que no tienes que escribirla desde cero.

A continuación, se explica cómo utilizarlo como función de activación en una red neuronal simple:

import torch
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(10, 20),
    nn.Tanh(),
    nn.Linear(20, 1)
)

x = torch.randn(5, 10)
output = model(x)
print(output)

tensor([[ 0.0910],
               [-0.0994],
               [-0.0583],  
               [-0.2177],
               [-0.2546]], grad_fn=<AddmmBackward0>)

También puedes aplicar tanh directamente a tensores:

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = torch.tanh(x)
print(output)

tensor([-0.9640, -0.7616, 0.0000, 0.7616, 0.9640])

Observa cómo los resultados son simétricos alrededor de cero: las entradas negativas producen resultados negativos, y la función trata ambos lados por igual. Esta distribución equilibrada mantiene tu red estable durante el entrenamiento y evita el desplazamiento del sesgo que se observaría con funciones como la sigmoide.

Cuándo se utiliza Tanh

Elige la función Tanh cuando tu modelo se beneficie de activaciones centradas o cuando trabajes con redes más pequeñas o recurrentes.

Es especialmente eficaz cuando:

• Estás entrenando RNN o LSTM que necesitan activaciones equilibradas. Estas arquitecturas se basan en Tanh para mantener estados internos fluidos a lo largo de los intervalos de tiempo, al tiempo que permiten el flujo de señales positivas y negativas.
• Estás modelando objetivos continuos o suaves. El flujo de gradiente suave de Tanh funciona bien cuando tus resultados deben ser continuos y limitados, como la predicción de valores que se encuentran naturalmente dentro de un rango.
• Quieres gradientes estables y diferenciables, pero no necesitas la dispersión de ReLU. Si tu red no es lo suficientemente profunda como para beneficiarse de la ventaja de velocidad de ReLU, Tanh te ofrece un comportamiento de entrenamiento más predecible.

Por el contrario, evita Tanh en arquitecturas muy profundas en las que los gradientes desaparecidos sean un problema. ReLU o GELU son más adecuados en este caso porque no se saturan con valores positivos.

Conclusión

En resumen, la función Tanh se sitúa entre la simplicidad de Sigmoid y la velocidad de ReLU.

Es suave, simétrico y sigue siendo relevante en el aprendizaje profundo, especialmente cuando lo que más importa son las activaciones equilibradas. No lo encontrarás en todas las arquitecturas modernas, pero tiene su lugar cuando necesitas salidas centradas y un flujo de gradiente estable.

Si no estás seguro de si utilizar Tanh o no, solo tienes que seguir estas pautas:

• Utiliza ReLU para redes grandes y profundas. Es más rápido, funciona bien con el hardware moderno y evita los gradientes que desaparecen para los valores positivos.
• Utiliza Tanh cuando necesites estabilidad, simetría y un flujo de degradado más suave. Esto significa redes recurrentes, arquitecturas más pequeñas y casos en los que las activaciones centradas en cero mejoran la convergencia.

Realiza experimentos, compara resultados y deja que tus datos decidan qué activación se adapta mejor a tu tarea. ¿Quieres saber más? Inscríbete en nuestro programa de Científico de machine learning en Python para comprender los entresijos del aprendizaje supervisado, no supervisado y profundo.