Tanh Function: Why Zero-Centered Outputs Matter for Neural Networks

Is your neural network stuck at 60% accuracy, and you can't figure out why?

You've tweaked the learning rate, added more layers, and played with the batch size. Nothing works. The training loss barely budges after the first few epochs. You start questioning your entire setup. Maybe the data's bad, maybe the architecture's wrong. But what’s really happening is your activation function is pushing all outputs in one direction, which makes it impossible for the network to learn balanced patterns.

Tanh (hyperbolic tangent) solves this by centering outputs around zero, ranging from -1 to 1. This helps your models converge faster and keeps gradients flowing symmetrically during backpropagation.

In this article, you'll learn what tanh is, how it works mathematically, when to use it over ReLU or sigmoid, and how to implement it in PyTorch. If you're new to deep learning, check out our in-depth guide to activation functions in neural networks.

What Is the Tanh Function?

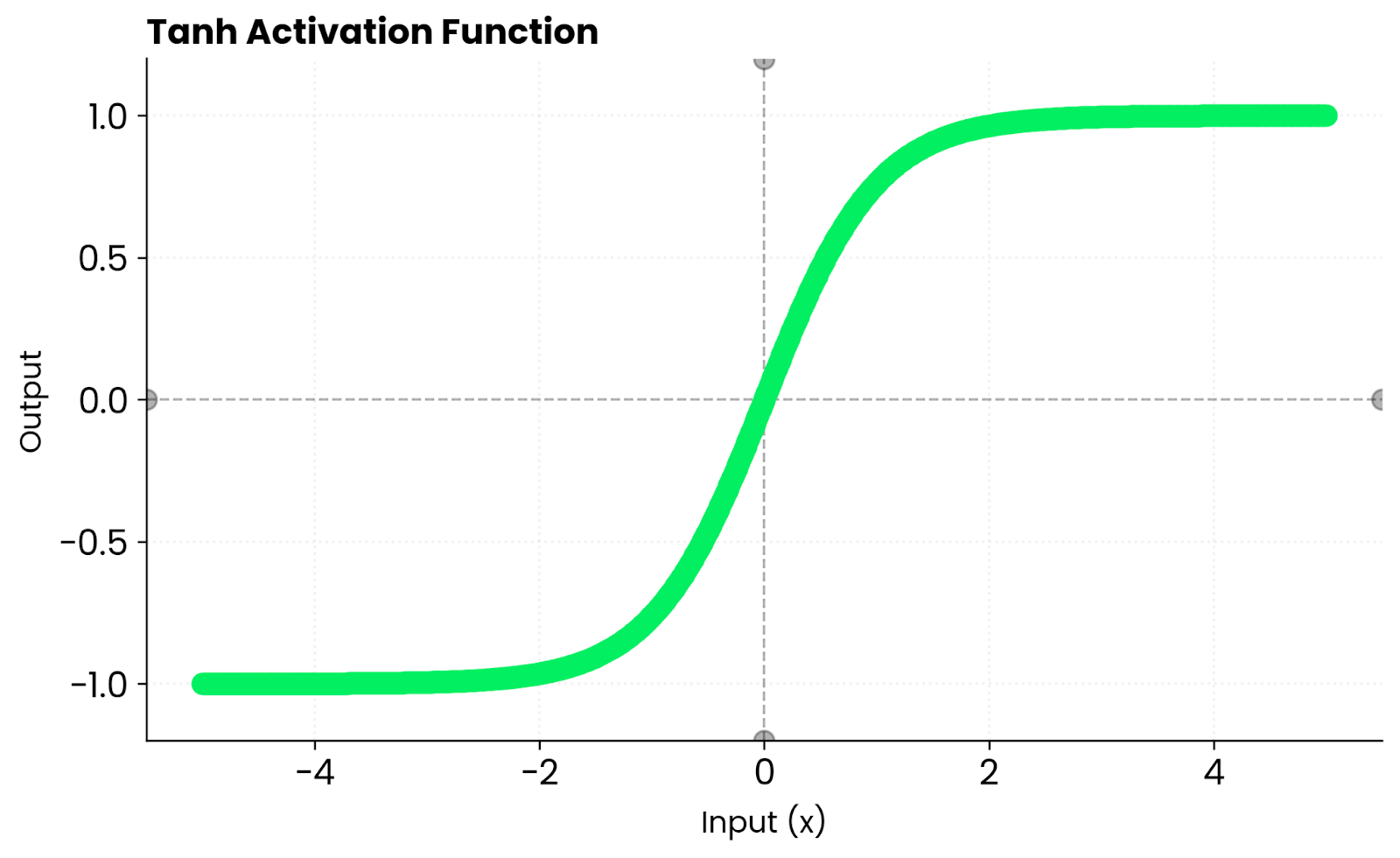
The tanh function maps any input to a value between -1 and 1.

It's a smooth, S-shaped curve defined by this formula:

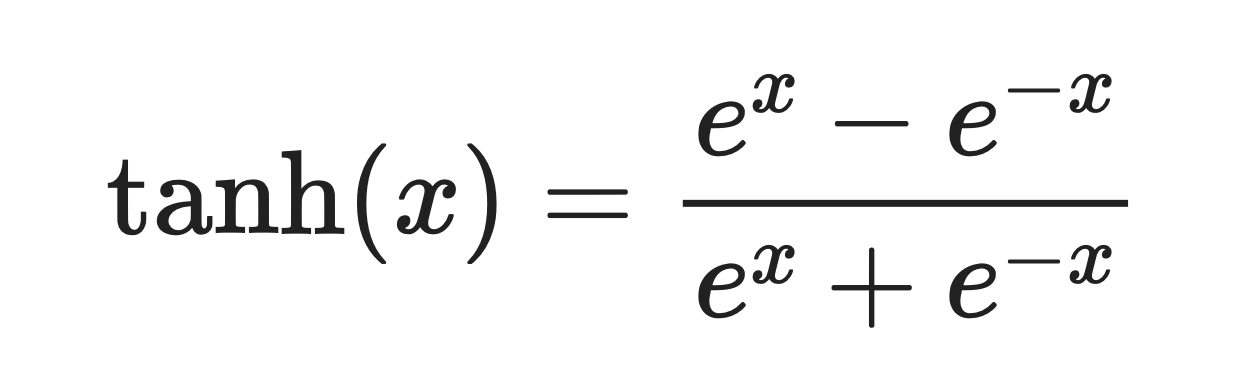
Tanh function. Image by Author

The function behaves predictably at extremes. When you give it a large positive number, it outputs something close to 1. For a large negative number, you’ll get something close to -1.

Around zero, tanh behaves almost linearly. This means gradients flow smoothly during backpropagation instead of getting squashed or distorted.

For comparison, sigmoid only outputs positive values between 0 and 1. Tanh outputs both positive and negative numbers. It keeps activations balanced around zero, which helps optimization converge faster in many network architectures.

You'll see tanh used most often in recurrent networks and anywhere centered activations improve stability.

Mathematical and Computational Properties

Tanh has a few mathematical properties every aspiring machine learning engineer must know.

Smooth and differentiable

Tanh is infinitely differentiable and smooth everywhere.

This matters for gradient-based optimization. You won't hit sharp corners like you do with ReLU, where the derivative jumps from 0 to 1 instantly. Smooth gradients mean more predictable weight updates during backpropagation.

Zero-centered output

Sigmoid outputs values between 0 and 1. Tanh outputs values between -1 and 1.

When activations stay balanced around zero, your network converges faster. Weight updates don't get biased in one direction, and gradients flow more evenly through layers.

Bounded and stable

Tanh's output range is fixed between -1 and 1.

These bounds prevent numerical instability. If you're working with networks that can't handle exploding activations, tanh keeps things under control without clipping or special handling.

Behavior at extremes

For large positive values, tanh approaches 1. For large negative values, it approaches -1.

This symmetry keeps activations centered and prevents the bias shift you see with non-zero-centered functions like sigmoid. In deep networks, that property helps weight updates propagate more evenly through layers - your network doesn't develop a preference for positive or negative values.

Derivative of tanh

The derivative of tanh is:

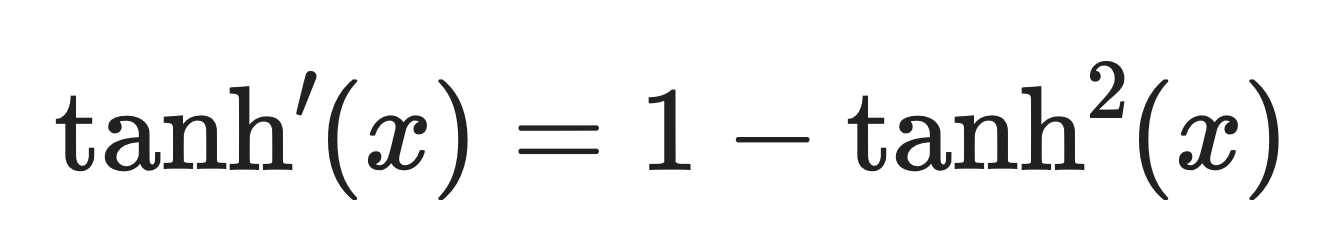
Tanh derivative. Image by Author.

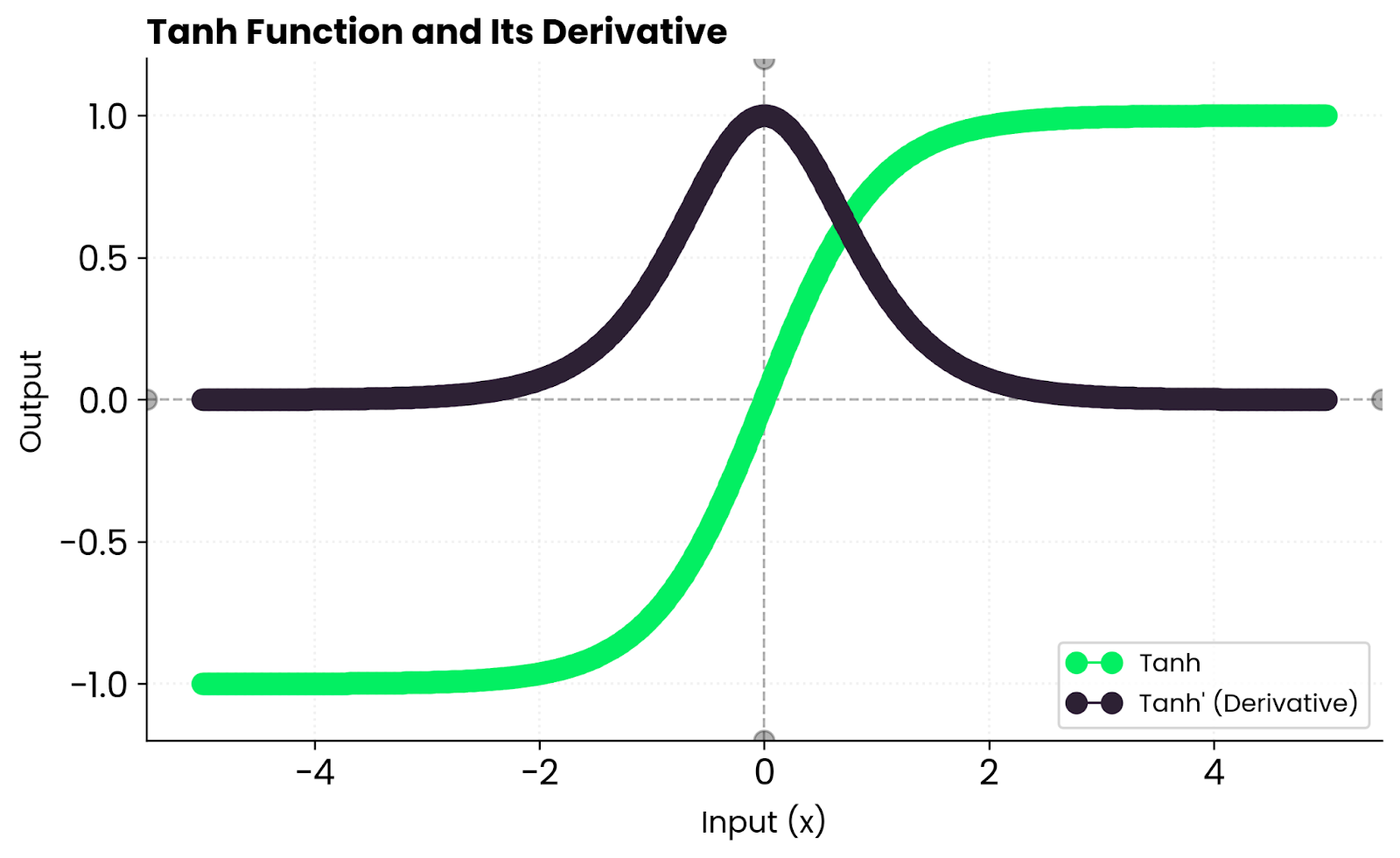
This means gradients are strong near zero but shrink toward the edges as the function saturates. When tanh(x) is close to 1 or -1, the derivative approaches zero, which slows down learning for those neurons.

In practice, you get stable learning for moderate inputs but potential vanishing gradients when inputs are too large or too small. This is why deep networks often prefer ReLU - it doesn't saturate for positive values.

Tanh vs. Other Functions

Tanh isn't the only activation function out there, and understanding how it compares to alternatives helps you pick the right one for your network.

Sigmoid is tanh's close relative. In fact, tanh is just a scaled and shifted version of sigmoid:

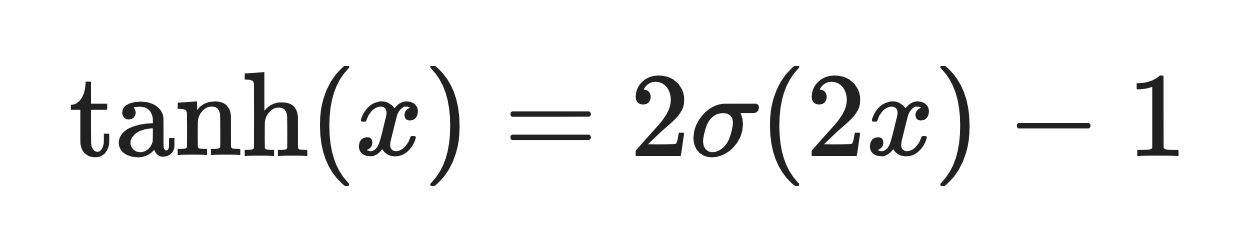
Where σ(x) is the sigmoid function.

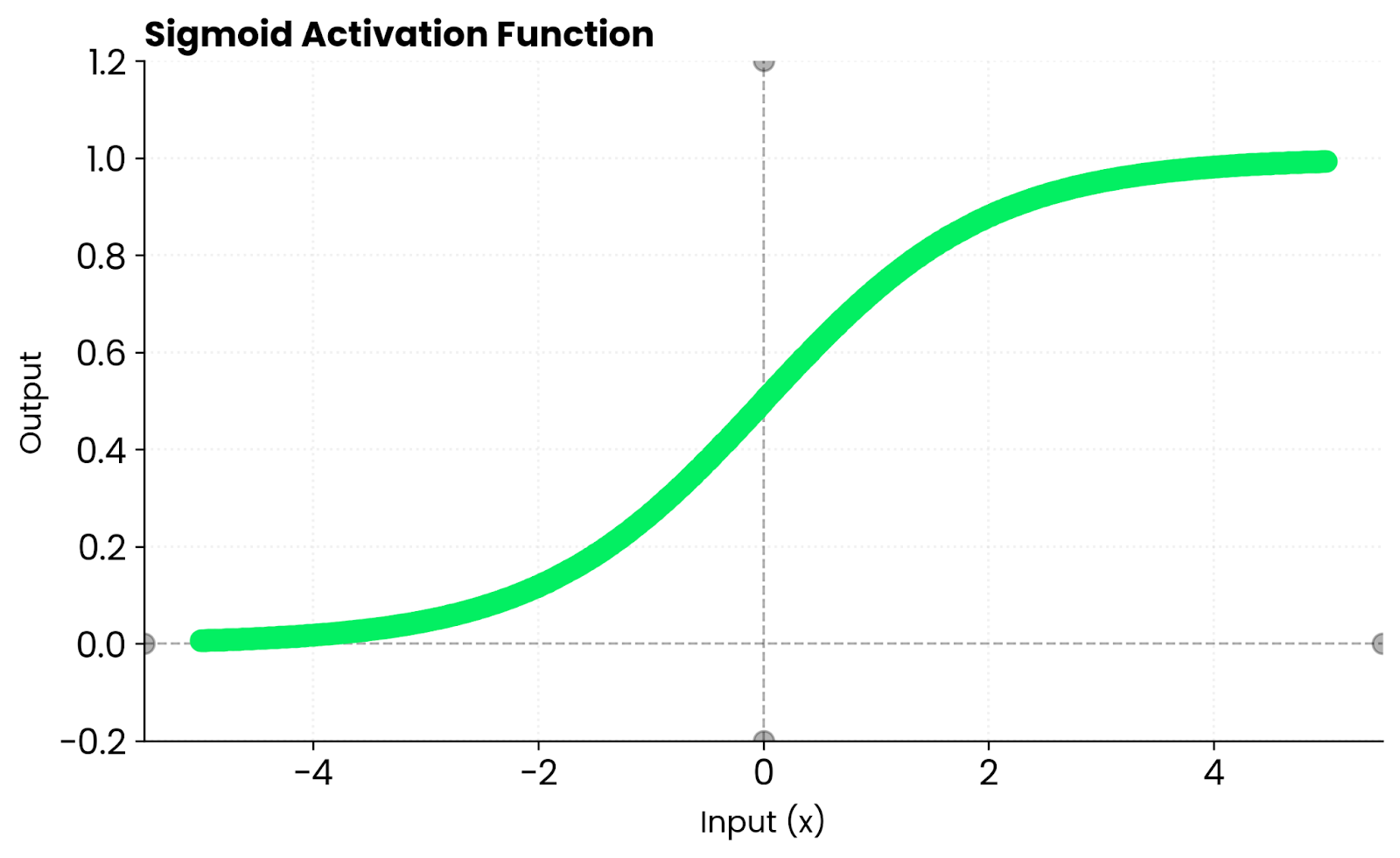
Sigmoid function. Image by Author

The key difference is that Sigmoid outputs values between 0 and 1, while tanh outputs values between -1 and 1. That zero-centering makes tanh converge faster in most cases.

ReLU takes a different approach. It outputs zero for negative inputs and passes positive inputs unchanged. This creates sparsity, meaning many neurons stay inactive, which speeds up training. But ReLU kills gradients for negative values. Tanh doesn't have this issue because it maintains non-zero gradients for negative inputs. It saturates at both extremes, which can slow learning when inputs get too large or too small.

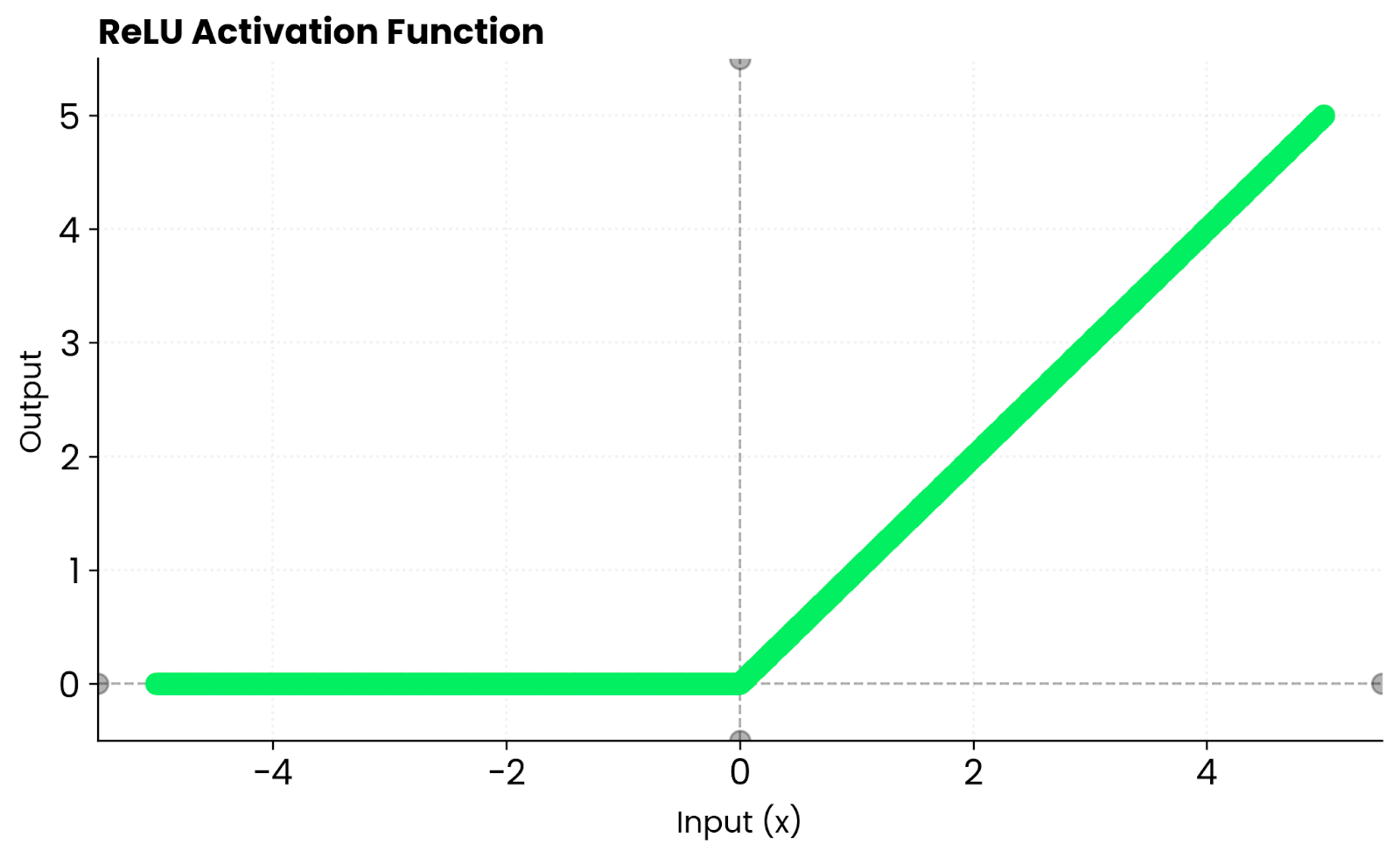
ReLU function. Image by Author

Softsign looks similar to tanh. Both are smooth, S-shaped curves. But tanh converges faster near zero because its slope is steeper. This means stronger gradients during the early stages of training, which can help your network learn faster before inputs start hitting the saturation zones.

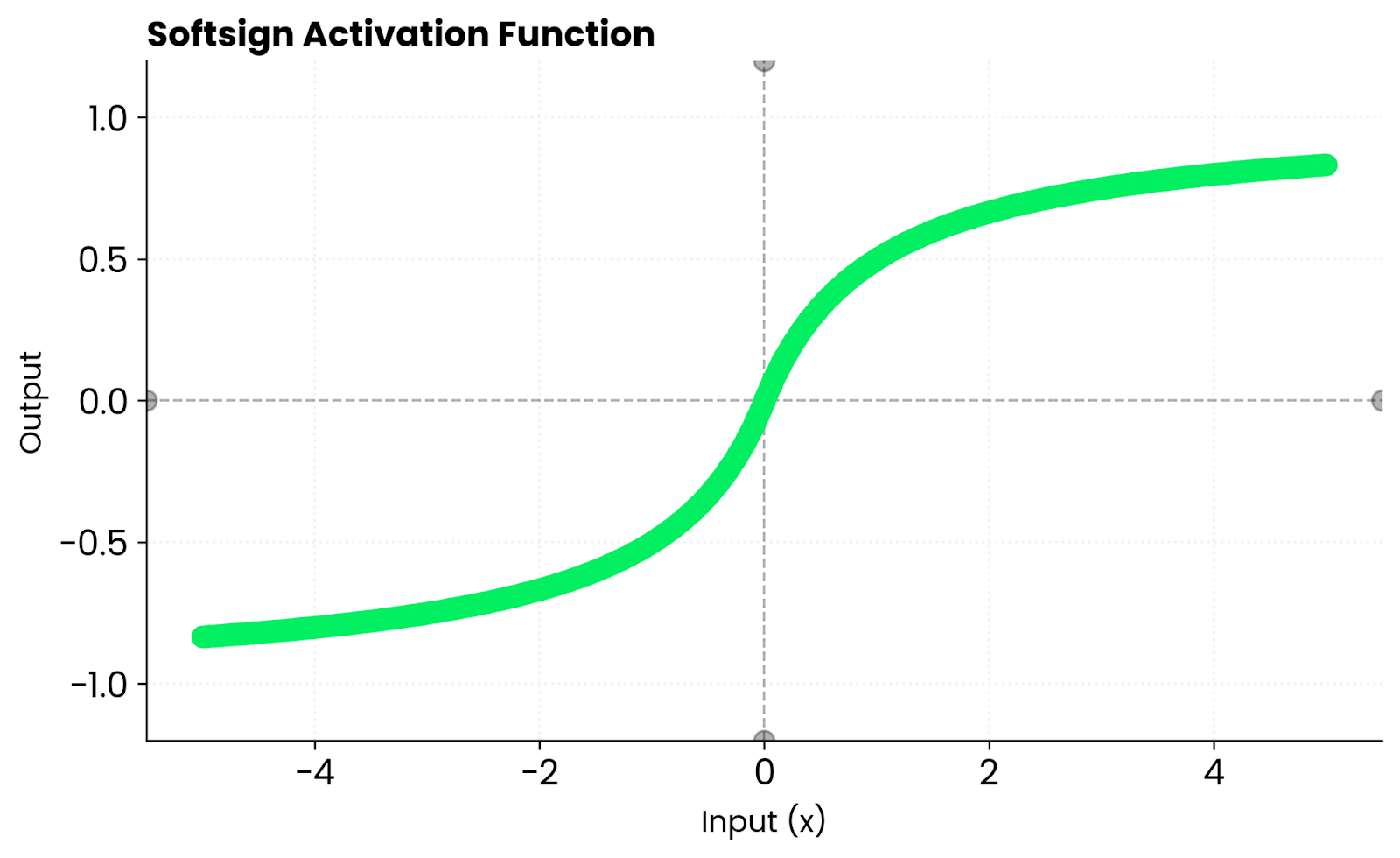
Softsign function. Image by Author

I’m only scratching the surface with these activation functions. If you’re interested in alternatives to Tanh and ReLU, read our in-depth guides to Softmax and Softplus.

Advantages of Tanh

If you’re deciding if Tanh is worth trying out, here are some advantages to consider that might give you a more accurate model in the end.

Zero-centered output

Tanh produces balanced outputs around zero.

This reduces bias in weight updates. When your activations center around zero instead of being skewed positive like sigmoid, gradients don't pull weights in one direction more than the other. It all ends up with faster convergence and more stable training.

Stronger gradients near zero

Tanh has a steep slope near zero.

This means stronger gradients during backpropagation compared to the sigmoid. Your network learns faster in the early stages of training when most activations sit near zero. On the other hand, Sigmoid's gentler slope makes those initial updates weaker and slower.

Smooth gradient flow

Tanh's derivatives are continuous everywhere.

There are no sudden jumps or discontinuities. This gives you a more stable optimization compared to piecewise functions like ReLU, where the derivative switches abruptly from 0 to 1 at zero. Smooth gradients mean predictable weight updates throughout training.

Ideal for recurrent networks

RNNs, LSTMs, and GRUs rely on tanh in their hidden layers.

These architectures need to maintain smooth internal states across time steps. Tanh lets both positive and negative signals flow through while keeping values bounded. This balance prevents exploding activations and helps the network remember information over longer sequences.

Limitations and Trade-Offs

Before diving into the code, I’ll cover a couple of areas where Tanh might fall short.

Vanishing gradients

When inputs move far from zero, gradients approach zero.

This happens because tanh saturates at -1 and 1. Once your activations hit these extremes, the derivative becomes tiny, and weight updates slow to a crawl. In very deep networks, this problem compounds because gradients shrink as they backpropagate through each layer until learning practically stops.

Slower training

Tanh doesn't create sparsity.

Every neuron stays active to some degree, unlike ReLU where negative inputs produce zero output. This means your network processes more information per forward pass, which sounds good but actually slows things down. ReLU's sparsity makes training faster because inactive neurons entirely skip the computation.

Less hardware optimization

Modern frameworks and hardware accelerators favor ReLU.

Tanh operations involve exponentials, which are more expensive to compute than ReLU's simple max(0, x) operation. GPU kernels and specialized AI chips are optimized for ReLU because it's become the default in most architectures. This means tanh will run slower on the same hardware, even with identical network architectures.

Tanh in PyTorch

PyTorch natively gives you an implementation of the Tanh function, meaning you don’t have to write it from scratch.

Here's how to use it as an activation function in a simple neural network:

import torch
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(10, 20),
    nn.Tanh(),
    nn.Linear(20, 1)
)

x = torch.randn(5, 10)
output = model(x)
print(output)

tensor([[ 0.0910],
               [-0.0994],
               [-0.0583],  
               [-0.2177],
               [-0.2546]], grad_fn=<AddmmBackward0>)

You can also apply tanh directly to tensors:

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = torch.tanh(x)
print(output)

tensor([-0.9640, -0.7616, 0.0000, 0.7616, 0.9640])

Notice how the outputs are symmetric around zero - negative inputs produce negative outputs, and the function treats both sides equally. This balanced distribution keeps your network stable during training and prevents the bias shift you'd see with functions like sigmoid.

When Tanh is Used

Choose the Tanh function when your model benefits from centered activations or when working with smaller or recurrent networks.

It's especially effective when:

• You're training RNNs or LSTMs that need balanced activations. These architectures rely on Tanh to maintain smooth internal states across time steps while allowing both positive and negative signals to flow through.
• You're modeling continuous or smooth targets. Tanh's smooth gradient flow works well when your outputs need to be continuous and bounded, like predicting values that naturally fall within a range.
• You want stable, differentiable gradients but don't need the sparsity of ReLU. If your network isn't deep enough to benefit from ReLU's speed advantage, Tanh gives you more predictable training behavior.

On the contrary, avoid Tanh in very deep architectures where vanishing gradients are a concern. ReLU or GELU are better fits there because they don't saturate for positive values.

Conclusion

To summarize, the Tanh function sits between Sigmoid's simplicity and ReLU's speed.

It's smooth, symmetric, and still relevant in deep learning, especially where balanced activations are what matter most. You won't find it in every modern architecture, but it has its place when you need centered outputs and stable gradient flow.

If you’re unsure whether to use Tanh or not, just follow these guidelines:

• Use ReLU for large, deep networks. It's faster, works well with modern hardware, and avoids vanishing gradients for positive values.
• Use Tanh when you need stability, symmetry, and smoother gradient flow. This means recurrent networks, smaller architectures, and cases where zero-centered activations improve convergence.

Run experiments, compare results, and let your data decide which activation suits your task best. Want to learn more? Enroll in our Machine Learning Scientist in Python track to grasp the ins and outs of supervised, unsupervised, and deep learning.