Fonction Tanh : Pourquoi les sorties centrées sur zéro sont importantes pour les réseaux neuronaux

Votre réseau neuronal est-il bloqué à 60 % de précision et vous ne comprenez pas pourquoi ?

Vous avez ajusté le taux d'apprentissage, ajouté des couches supplémentaires et modifié la taille des lots. Rien ne fonctionne. La perte d'entraînement ne varie pratiquement pas après les premières époques. Vous commencez à remettre en question l'ensemble de votre configuration. Il se peut que les données soient incorrectes ou que l'architecture soit inadéquate. Cependant, ce qui se produit réellement, c'est que votre fonction d'activation oriente toutes les sorties dans une seule direction, ce qui empêche le réseau d'apprendre des modèles équilibrés.

La tangente hyperbolique (Tanh) résout ce problème en centrant les résultats autour de zéro, dans une plage comprise entre -1 et 1. Cela permet à vos modèles de converger plus rapidement et maintient la symétrie des gradients pendant la rétropropagation.

Dans cet article, vous découvrirez ce qu'est la fonction tanh, son fonctionnement mathématique, quand l'utiliser plutôt que ReLU ou sigmoid, et comment l'implémenter dans PyTorch. Si vous débutez dans le domaine du deep learning, nous vous invitons à consulter notre guide détaillé sur les fonctions d'activation dans les réseaux neuronaux.

Qu'est-ce que la fonction tanh ?

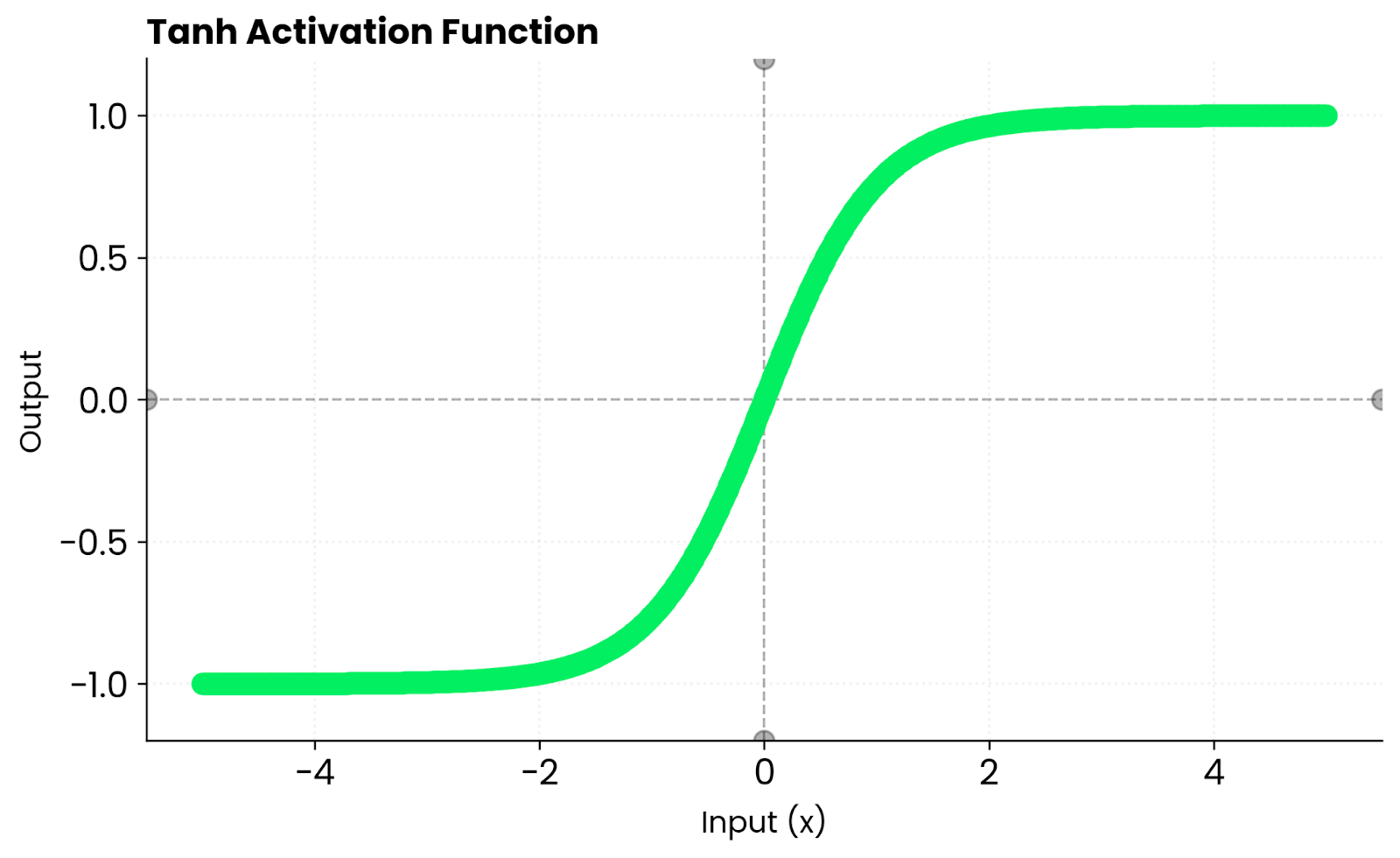
La fonction tanh transforme toute entrée en une valeur comprise entre -1 et 1.

Il s'agit d'une courbe lisse en forme de S définie par la formule suivante :

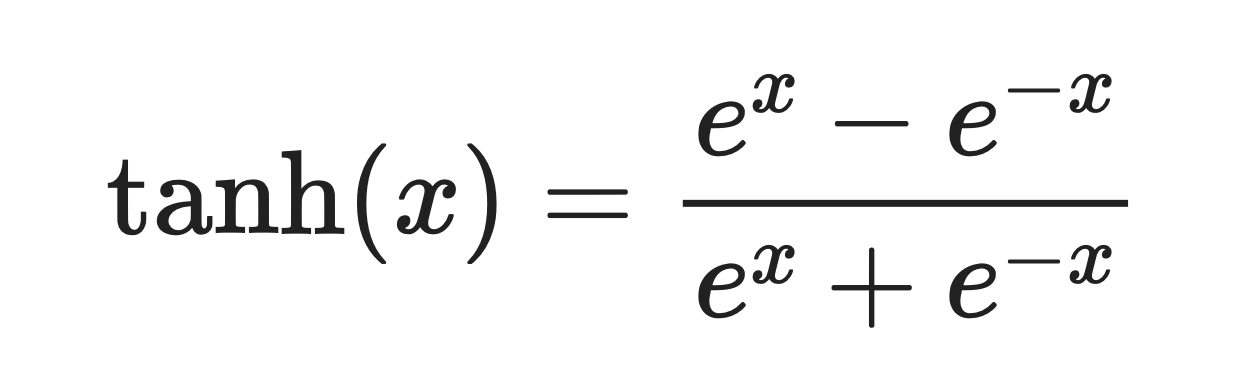
Fonction tanh. Image par l'auteur

La fonction se comporte de manière prévisible dans les cas extrêmes. Lorsque vous lui attribuez un grand nombre positif, il affiche une valeur proche de 1. Pour un grand nombre négatif, vous obtiendrez un résultat proche de -1.

Autour de zéro, la fonction tanh se comporte de manière presque linéaire. Cela signifie que les gradients s'écoulent de manière fluide pendant la rétropropagation au lieu d'être écrasés ou déformés.

À titre de comparaison, la fonction sigmoïde ne produit que des valeurs positives comprises entre 0 et 1. Tanh génère à la fois des nombres positifs et négatifs. Il maintient les activations équilibrées autour de zéro, ce qui contribue à accélérer la convergence de l'optimisation dans de nombreuses architectures réseau.

Vous constaterez que la fonction tanh est le plus souvent utilisée dans les réseaux récurrents et partout où les activations centrées améliorent la stabilité.

Propriétés mathématiques et informatiques

Tanh possède certaines propriétés mathématiques que tout ingénieur en apprentissage automatique en devenir doit connaître.

Lisse et différentiable

Tanh est infiniment dérivable et régulière partout.

Ceci est pertinent pour l'optimisation basée sur le gradient. Vous ne rencontrerez pas de coins pointus comme avec ReLU, où la dérivée passe instantanément de 0 à 1. Des gradients réguliers permettent des mises à jour plus prévisibles du poids lors de la rétropropagation.

Sortie centrée sur zéro

La fonction sigmoïde génère des valeurs comprises entre 0 et 1. Tanh génère des valeurs comprises entre -1 et 1.

Lorsque les activations restent équilibrées autour de zéro, votre réseau converge plus rapidement. Les mises à jour de poids ne sont pas biaisées dans une seule direction, et les gradients s'écoulent de manière plus uniforme à travers les couches.

Limité et stable

La plage de sortie de Tanh est comprise entre -1 et 1.

Ces limites permettent d'éviter l'instabilité numérique. Si vous travaillez avec des réseaux qui ne peuvent pas gérer les activations explosives, tanh permet de garder le contrôle sans écrêtage ni traitement particulier.

Comportement dans des situations extrêmes

Pour les grandes valeurs positives, tanh tend vers 1. Pour les grandes valeurs négatives, il tend vers -1.

Cette symétrie maintient les activations centrées et empêche le décalage de biais que l'on observe avec les fonctions non centrées sur zéro, telles que la fonction sigmoïde. Dans les réseaux profonds, cette propriété contribue à une propagation plus uniforme des mises à jour de poids à travers les couches - votre réseau ne développe pas de préférence pour les valeurs positives ou négatives.

Dérivée de tanh

La dérivée de tanh est :

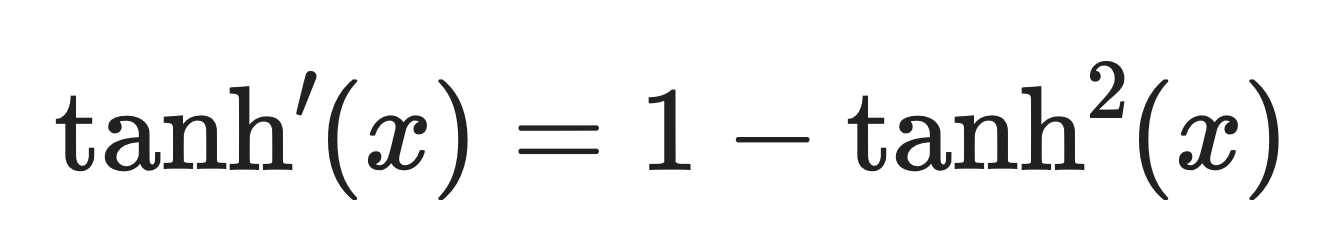
Dérivé de Tanh. Image fournie par l'auteur.

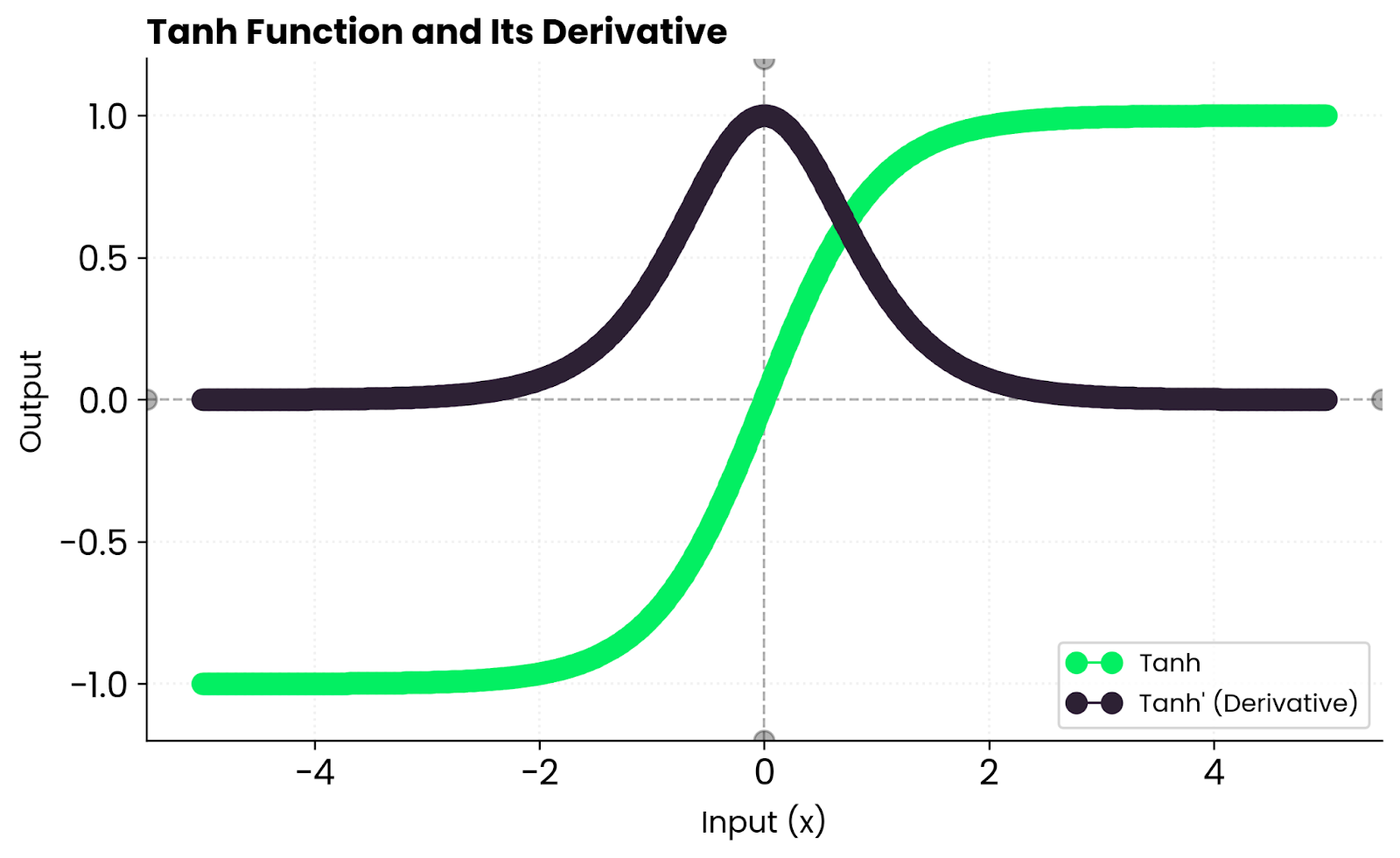
Cela signifie que les gradients sont importants près de zéro, mais diminuent vers les bords à mesure que la fonction atteint sa saturation. Lorsque tanh(x) est proche de 1 ou -1, la dérivée tend vers zéro, ce qui ralentit l'apprentissage de ces neurones.

En pratique, vous obtenez un apprentissage stable pour des entrées modérées, mais des gradients potentiellement nuls lorsque les entrées sont trop grandes ou trop petites. C'est pourquoi les réseaux profonds privilégient souvent la fonction ReLU, car elle ne sature pas pour les valeurs positives.

Tanh contre. Autres fonctions

Tanh n'est pas la seule fonction d'activation existante, et comprendre comment elle se compare aux autres vous aidera à choisir celle qui convient le mieux à votre réseau.

Sigmoid est étroitement lié à tanh. En réalité, la fonction tanh est simplement une version mise à l'échelle et décalée de la fonction sigmoïde :

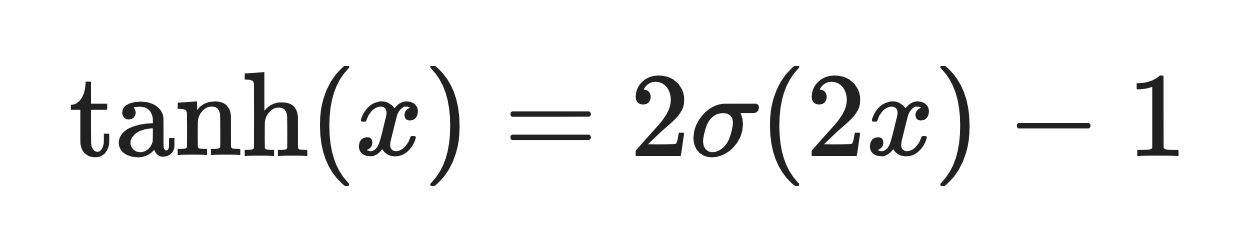
Où σ(x) est la fonction sigmoïde.

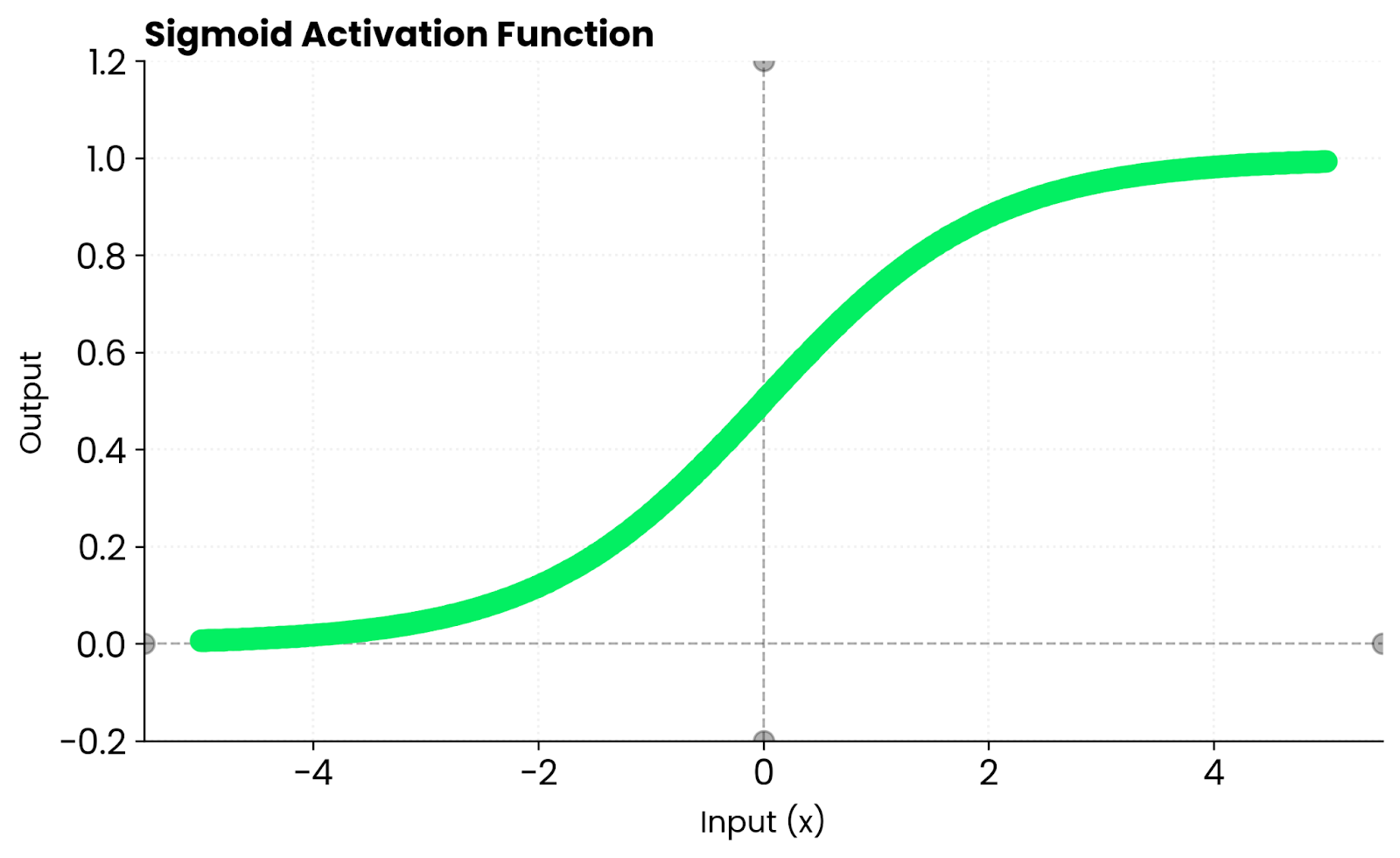
Fonction sigmoïde. Image par l'auteur

La principale différence réside dans le fait que la fonction sigmoïde génère des valeurs comprises entre 0 et 1, tandis que la fonction tanh génère des valeurs comprises entre -1 et 1. Ce centrage sur zéro permet à la fonction tanh de converger plus rapidement dans la plupart des cas.

ReLU adopte une approche différente. Il renvoie zéro pour les entrées négatives et transmet les entrées positives sans modification. Cela crée une parcimonie, ce qui signifie que de nombreux neurones restent inactifs, ce qui accélère l'entraînement. Cependant, ReLU élimine les gradients pour les valeurs négatives. Tanh ne présente pas ce problème, car il conserve des gradients non nuls pour les entrées négatives. Il atteint sa saturation aux deux extrêmes, ce qui peut ralentir l'apprentissage lorsque les entrées deviennent trop importantes ou trop faibles.

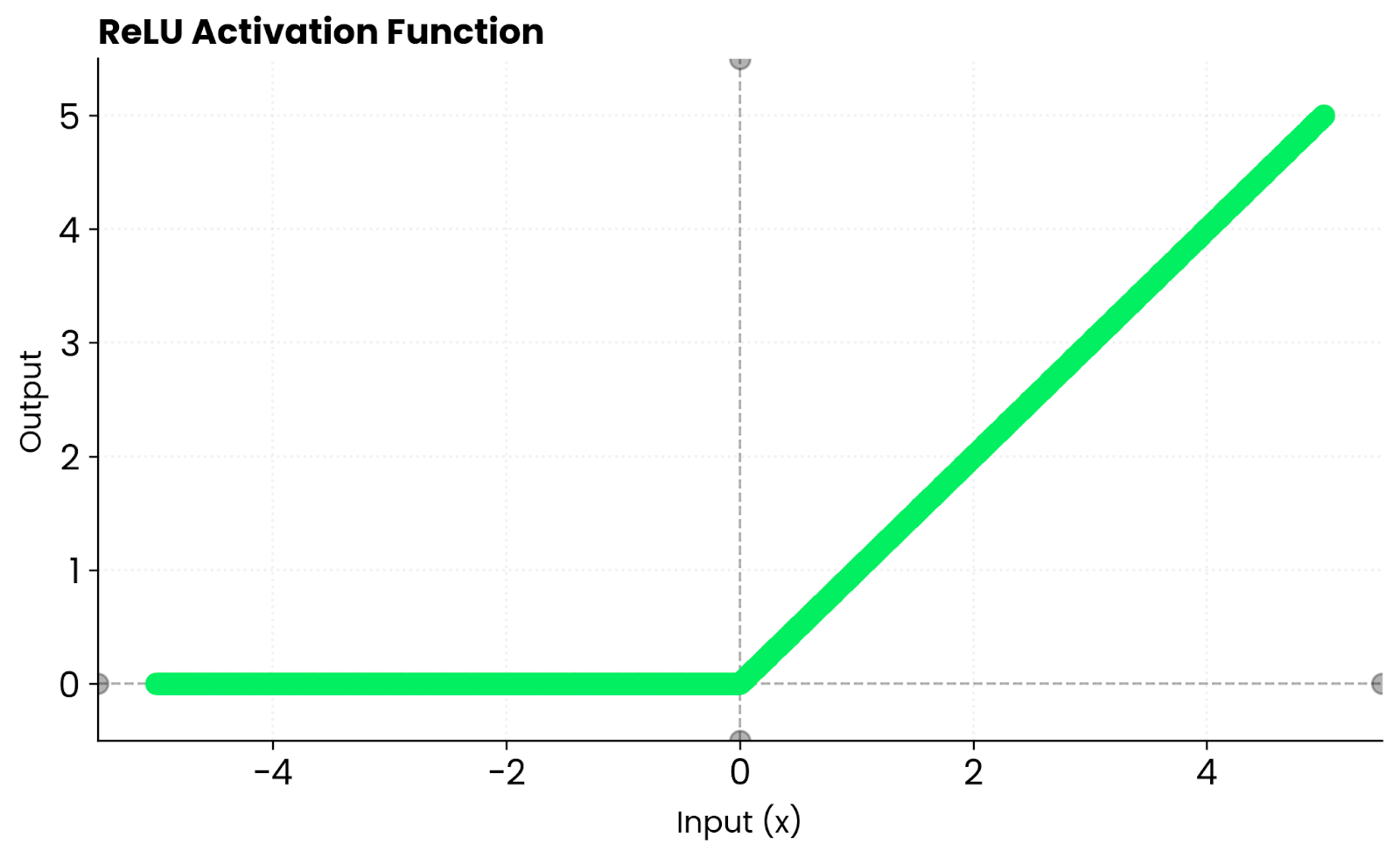
Fonction ReLU. Image par l'auteur

Softsign est similaire à tanh. Les deux sont des courbes lisses en forme de S. Cependant, tanh converge plus rapidement près de zéro, car sa pente est plus raide. Cela implique des gradients plus importants au cours des premières étapes de l'entraînement, ce qui peut aider votre réseau à apprendre plus rapidement avant que les entrées n'atteignent les zones de saturation.

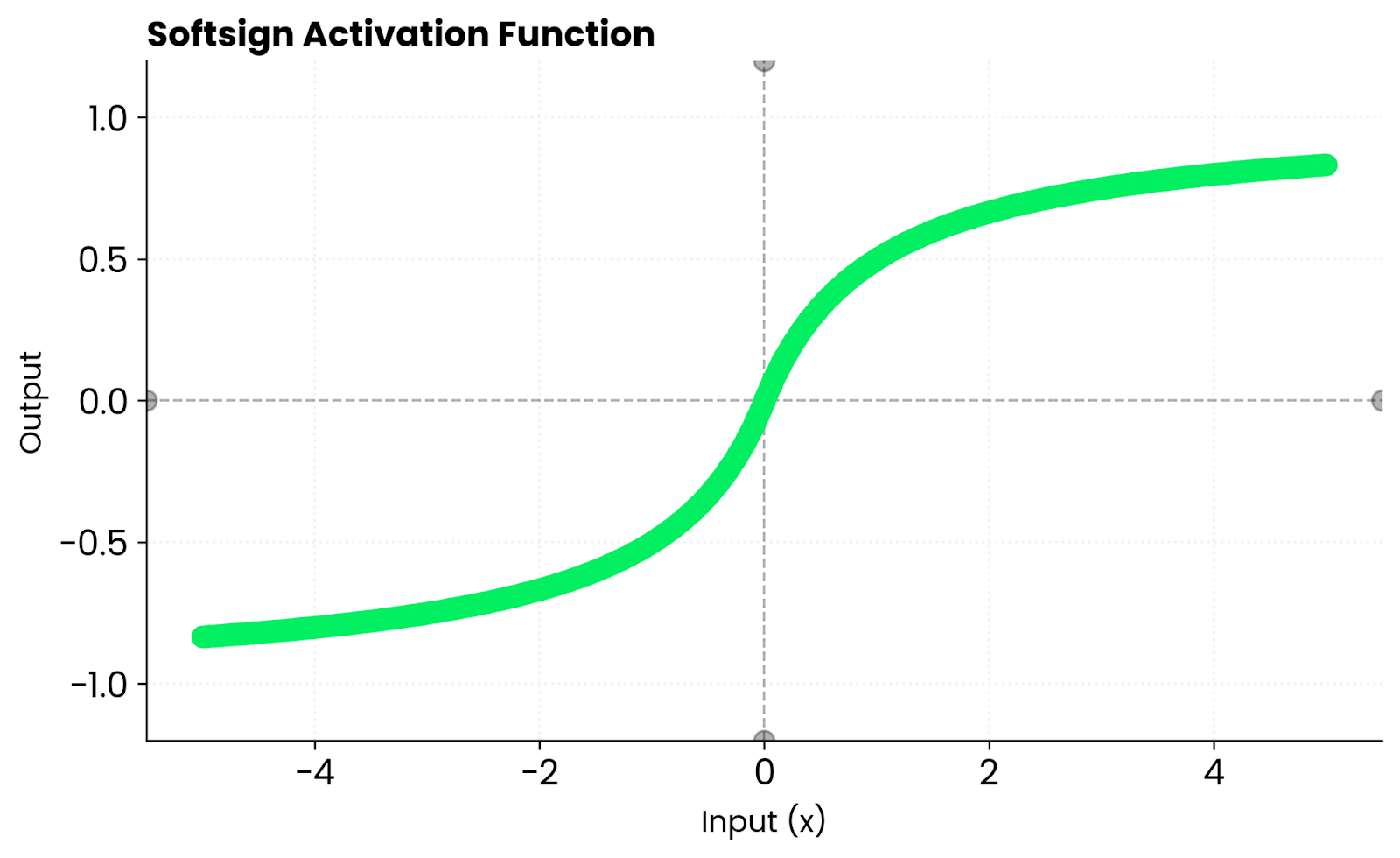
Fonction Softsign. Image par l'auteur

Je ne fais qu'effleurer le sujet avec ces fonctions d'activation. Si vous êtes intéressé par des alternatives à Tanh et ReLU, veuillez consulter notre guide détaillé intitulé « Alternatives à Softmax et Softplus ».

Avantages de Tanh

Si vous vous demandez si Tanh vaut la peine d'être essayé, voici quelques avantages à prendre en considération qui pourraient vous aider à vous faire une idée plus précise.

Sortie centrée sur zéro

Tanh produit des résultats équilibrés autour de zéro.

Cela permet de réduire les biais dans les mises à jour du poids. Lorsque vos activations sont centrées autour de zéro au lieu d'être biaisées vers le positif comme dans le cas de la fonction sigmoïde, les gradients n'influencent pas les poids dans une direction plus que dans l'autre. Tout cela aboutit à une convergence plus rapide et à un apprentissage plus stable.

Gradients plus forts proches de zéro

Tanh présente une pente abrupte proche de zéro.

Cela implique des gradients plus importants lors de la rétropropagation par rapport à la fonction sigmoïde. Votre réseau apprend plus rapidement au début de l'entraînement, lorsque la plupart des activations sont proches de zéro. D'un autre côté, la pente plus douce de Sigmoid rend ces mises à jour initiales plus faibles et plus lentes.

Flux de gradient régulier

Les dérivées de Tanh sont continues partout.

Il n'y a pas de sauts brusques ni de discontinuités. Cela vous offre une optimisation plus stable par rapport aux fonctions par morceaux telles que ReLU, où la dérivée passe brusquement de 0 à 1 à zéro. Des gradients réguliers garantissent des mises à jour prévisibles du poids tout au long de l'entraînement.

Idéal pour les réseaux récurrents

Les RNN, LSTM et GRU utilisent la fonction tanh dans leurs couches cachées.

Ces architectures doivent maintenir des états internes stables au fil des étapes temporelles. Tanh permet aux signaux positifs et négatifs de circuler tout en maintenant les valeurs dans des limites définies. Cet équilibre empêche les activations excessives et aide le réseau à mémoriser les informations sur des séquences plus longues.

Limites et compromis

Avant d'entrer dans le vif du sujet, je vais aborder quelques domaines dans lesquels Tanh pourrait présenter certaines limites.

Gradients de disparition

Lorsque les entrées s'éloignent de zéro, les gradients tendent vers zéro.

Cela se produit parce que tanh sature à -1 et 1. Une fois que vos activations atteignent ces extrêmes, la dérivée devient minime et les mises à jour de poids ralentissent considérablement. Dans les réseaux très profonds, ce problème s'aggrave car les gradients diminuent à mesure qu'ils se propagent à travers chaque couche jusqu'à ce que l'apprentissage s'arrête pratiquement.

Entraînement plus lent

Tanh ne crée pas de parcimonie.

Chaque neurone reste actif dans une certaine mesure, contrairement à ReLU où les entrées négatives produisent une sortie nulle. Cela signifie que votre réseau traite davantage d'informations par passe avant, ce qui peut sembler avantageux, mais ralentit en réalité le processus. La rareté de ReLU accélère l'entraînement, car les neurones inactifs ignorent complètement le calcul.

Moins d'optimisation matérielle

Les frameworks modernes et les accélérateurs matériels privilégient ReLU.

Les opérations Tanh impliquent des exponentielles, qui sont plus coûteuses à calculer que la simple opération max(0, x) de ReLU. Les noyaux GPU et les puces IA spécialisées sont optimisés pour ReLU, car cette fonction est devenue la norme dans la plupart des architectures. Cela signifie que tanh fonctionnera plus lentement sur le même matériel, même avec des architectures réseau identiques.

Tanh dans PyTorch

PyTorch fournit nativement une implémentation de la fonction Tanh, ce qui signifie que vous n'avez pas besoin de la créer à partir de zéro.

Voici comment l'utiliser comme fonction d'activation dans un réseau neuronal simple :

import torch
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(10, 20),
    nn.Tanh(),
    nn.Linear(20, 1)
)

x = torch.randn(5, 10)
output = model(x)
print(output)

tensor([[ 0.0910],
               [-0.0994],
               [-0.0583],  
               [-0.2177],
               [-0.2546]], grad_fn=<AddmmBackward0>)

Vous pouvez également appliquer tanh directement aux tenseurs :

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = torch.tanh(x)
print(output)

tensor([-0.9640, -0.7616, 0.0000, 0.7616, 0.9640])

Veuillez noter que les sorties sont symétriques autour de zéro : les entrées négatives produisent des sorties négatives, et la fonction traite les deux côtés de manière égale. Cette répartition équilibrée assure la stabilité de votre réseau pendant l'entraînement et empêche le décalage de biais que l'on observe avec des fonctions telles que sigmoid.

Quand utiliser Tanh

Veuillez sélectionner la fonction Tanh lorsque votre modèle bénéficie d'activations centrées ou lorsque vous travaillez avec des réseaux plus petits ou récurrents.

Il est particulièrement efficace lorsque :

• Vous entraînez des RNN ou des LSTM qui nécessitent des activations équilibrées. Ces architectures s'appuient sur Tanh pour maintenir des états internes stables au fil du temps tout en permettant aux signaux positifs et négatifs de circuler.
• Vous modélisez des cibles continues ou lisses. Le flux de gradient lisse de Tanh est particulièrement efficace lorsque vos résultats doivent être continus et limités, comme pour prédire des valeurs qui se situent naturellement dans une certaine plage.
• Vous recherchez des gradients stables et différentiables, mais vous n'avez pas besoin de la parcimonie de ReLU. Si votre réseau n'est pas suffisamment profond pour tirer parti de l'avantage de vitesse de ReLU, Tanh vous offre un comportement d'entraînement plus prévisible.

Au contraire, il est recommandé d'éviter Tanh dans les architectures très profondes où la disparition des gradients est un problème. Les fonctions ReLU ou GELU sont plus adaptées dans ce cas, car elles ne saturent pas pour les valeurs positives.

Conclusion

En résumé, la fonction Tanh se situe entre la simplicité de Sigmoid et la rapidité de ReLU.

Il est fluide, symétrique et toujours pertinent dans l'apprentissage profond, en particulier lorsque les activations équilibrées sont primordiales. Vous ne le trouverez pas dans toutes les architectures modernes, mais il est utile lorsque vous avez besoin de sorties centrées et d'un flux de gradient stable.

Si vous hésitez à utiliser Tanh, veuillez suivre ces directives :

• Veuillez utiliser ReLU pour les réseaux volumineux et profonds. Il est plus rapide, fonctionne bien avec le matériel moderne et évite les gradients de disparition pour les valeurs positives.
• Veuillez utiliser Tanh lorsque vous avez besoin de stabilité, de symétrie et d'un dégradé plus fluide. Cela implique des réseaux récurrents, des architectures plus petites et des cas où les activations centrées sur zéro améliorent la convergence.

Effectuez des essais, comparez les résultats et laissez vos données déterminer quelle activation convient le mieux à votre tâche. Souhaitez-vous en savoir davantage ? Inscrivez-vous à notre cursus Machine Learning Scientist in Python pour acquérir une compréhension approfondie de l'apprentissage supervisé, non supervisé et profond.