Tanh-Funktion: Warum nullzentrierte Ausgaben für neuronale Netze wichtig sind

Steckt dein neuronales Netzwerk bei einer Genauigkeit von 60 % fest und du weißt nicht, warum?

Du hast die Lernrate angepasst, mehr Schichten hinzugefügt und mit der Batchgröße rumgespielt. Nichts klappt. Der Trainingsverlust ändert sich nach den ersten paar Epochen kaum. Du fängst an, dein ganzes Setup in Frage zu stellen. Vielleicht sind die Daten schlecht, vielleicht stimmt die Architektur nicht. Aber eigentlich passiert Folgendes: Deine Aktivierungsfunktion schiebt alle Ausgaben in eine Richtung, was es dem Netzwerk unmöglich macht, ausgewogene Muster zu lernen.

Tanh (hyperbolische Tangente) macht das, indem es die Werte um Null herum zentriert, also von -1 bis 1. Das hilft deinen Modellen, schneller zu konvergieren, und sorgt dafür, dass die Gradienten während der Rückpropagation symmetrisch fließen.

In diesem Artikel erfährst du, was tanh ist, wie es mathematisch funktioniert, wann du es anstelle von ReLU oder Sigmoid verwenden solltest und wie du es in PyTorch umsetzen kannst. Wenn du dich noch nicht so gut mit Deep Learning auskennst, schau dir mal unseren ausführlichen Leitfaden zu Aktivierungsfunktionen in neuronalen Netzen an.

Was ist die Tanh-Funktion?

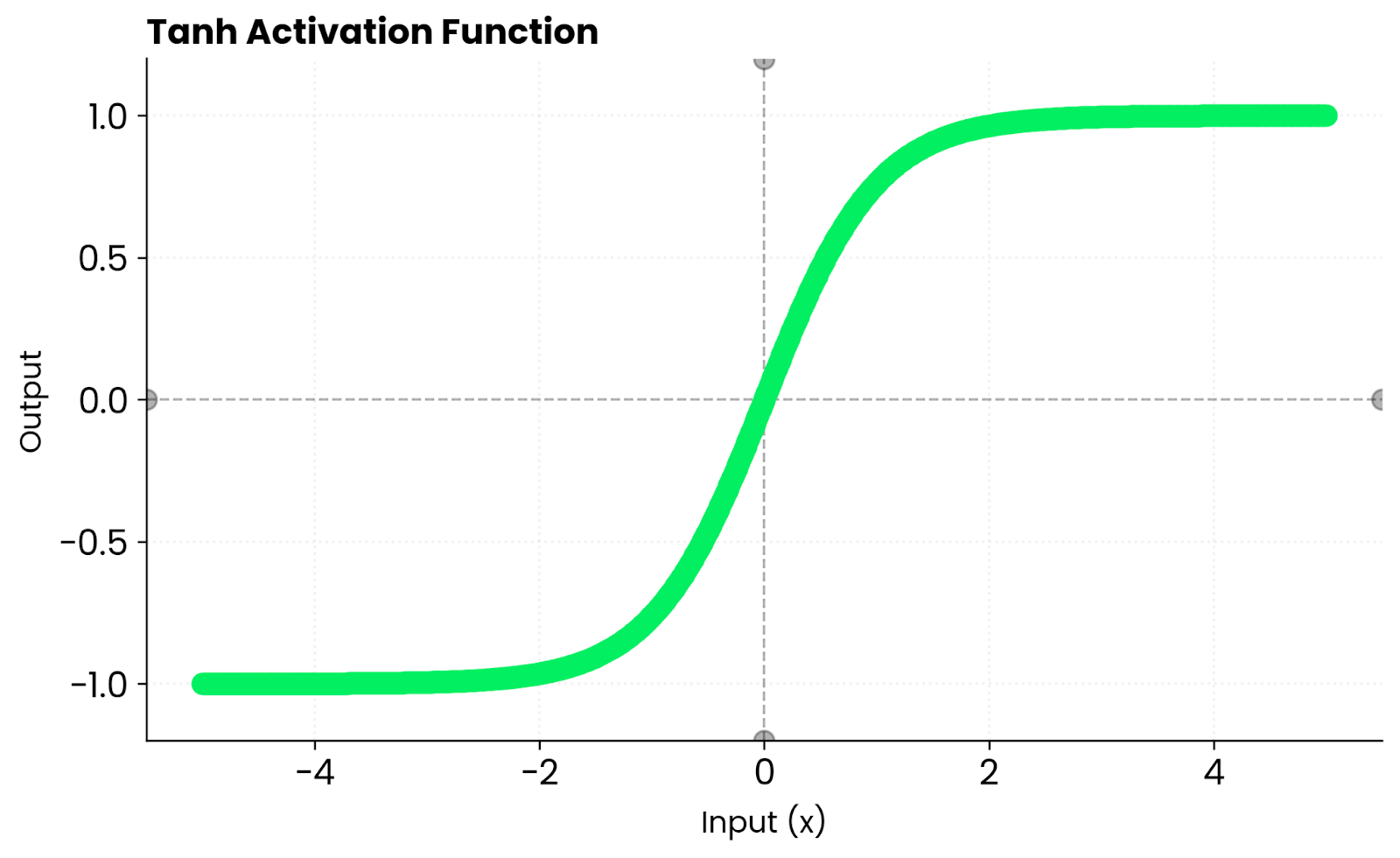
Die tanh-Funktion macht aus jedem Eingabewert einen Wert zwischen -1 und 1.

Es ist eine glatte, S-förmige Kurve, die durch diese Formel definiert ist:

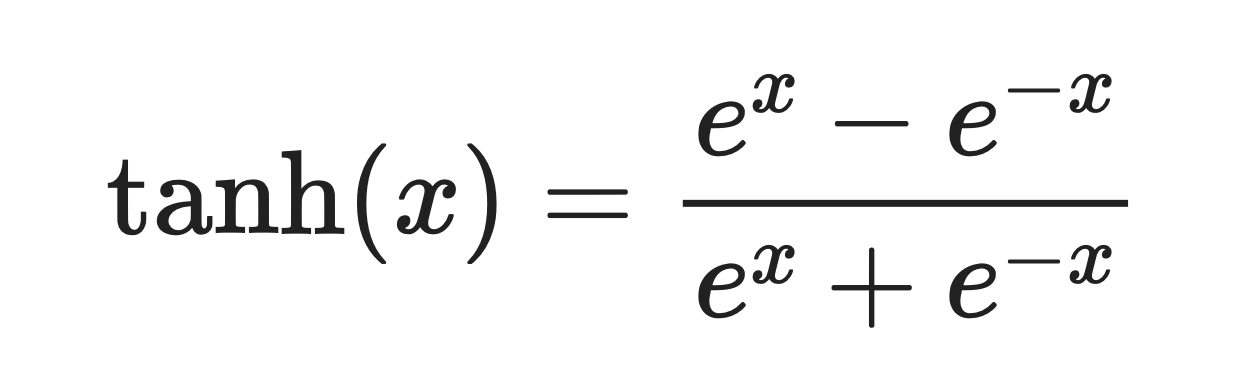
Tanh-Funktion. Bild vom Autor

Die Funktion verhält sich in Extremsituationen vorhersehbar. Wenn du eine große positive Zahl eingibst, gibt es was aus, das fast 1 ist. Bei einer großen negativen Zahl bekommst du einen Wert, der nahe bei -1 liegt.

Um den Nullpunkt herum verhält sich tanh fast linear. Das heißt, dass die Gradienten während der Rückpropagation flüssig fließen, anstatt gequetscht oder verzerrt zu werden.

Zum Vergleich: Sigmoid gibt nur positive Werte zwischen 0 und 1 raus. Tanh gibt sowohl positive als auch negative Zahlen aus. Es hält die Aktivierungen um den Nullpunkt herum ausgeglichen, was in vielen Netzwerkarchitekturen zu einer schnelleren Konvergenz der Optimierung beiträgt.

Du wirst sehen, dass tanh meistens in rekurrenten Netzen und überall dort verwendet wird, wo zentrierte Aktivierungen die Stabilität verbessern.

Mathematische und rechnerische Eigenschaften

Tanh hat ein paar mathematische Eigenschaften, die jeder angehende Machine-Learning-Ingenieur kennen sollte.

Glatt und differenzierbar

Tanh ist überall unendlich oft differenzierbar und glatt.

Das ist wichtig für die gradientenbasierte Optimierung. Du stößt nicht auf scharfe Ecken wie bei ReLU, wo die Ableitung sofort von 0 auf 1 springt. Glatte Gradienten bedeuten, dass die Gewichtsaktualisierungen während der Rückpropagation besser vorhersehbar sind.

Nullzentrierte Ausgabe

Sigmoid gibt Werte zwischen 0 und 1 aus. Tanh gibt Werte zwischen -1 und 1 aus.

Wenn die Aktivierungen um den Nullpunkt herum ausgeglichen bleiben, läuft dein Netzwerk schneller zusammen. Gewichtsaktualisierungen sind nicht einseitig verzerrt, und Gradienten fließen gleichmäßiger durch die Ebenen.

Begrenzt und stabil

Der Ausgangsbereich von Tanh liegt zwischen -1 und 1.

Diese Grenzen verhindern numerische Instabilität. Wenn du mit Netzwerken arbeitest, die mit explodierenden Aktivierungen nicht klarkommen, sorgt tanh dafür, dass alles unter Kontrolle bleibt, ohne dass es zu Clipping oder Sonderbehandlungen kommt.

Verhalten in Extremsituationen

Bei großen positiven Werten geht tanh gegen 1. Bei großen negativen Werten geht es gegen -1.

Diese Symmetrie hält die Aktivierungen in der Mitte und verhindert die Verschiebung der Verzerrung, die man bei Funktionen sieht, die nicht auf Null zentriert sind, wie zum Beispiel Sigmoid. In tiefen Netzwerken sorgt diese Eigenschaft dafür, dass sich Gewichtsaktualisierungen gleichmäßiger über die Schichten verteilen – dein Netzwerk entwickelt keine Vorliebe für positive oder negative Werte.

Ableitung von tanh

Die Ableitung von tanh ist:

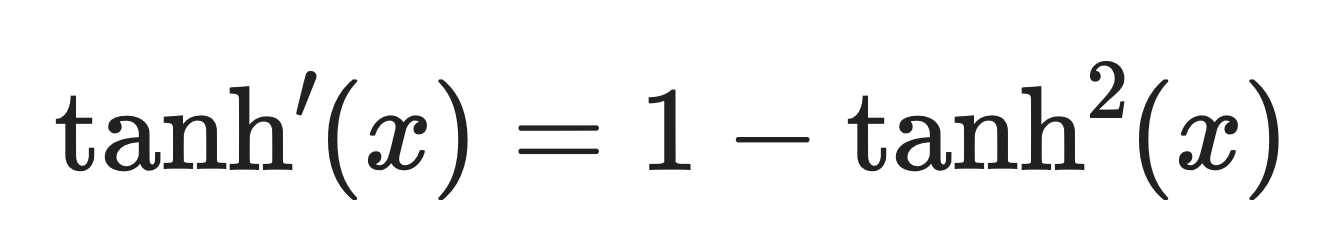
Tanh-Ableitung. Bild vom Autor.

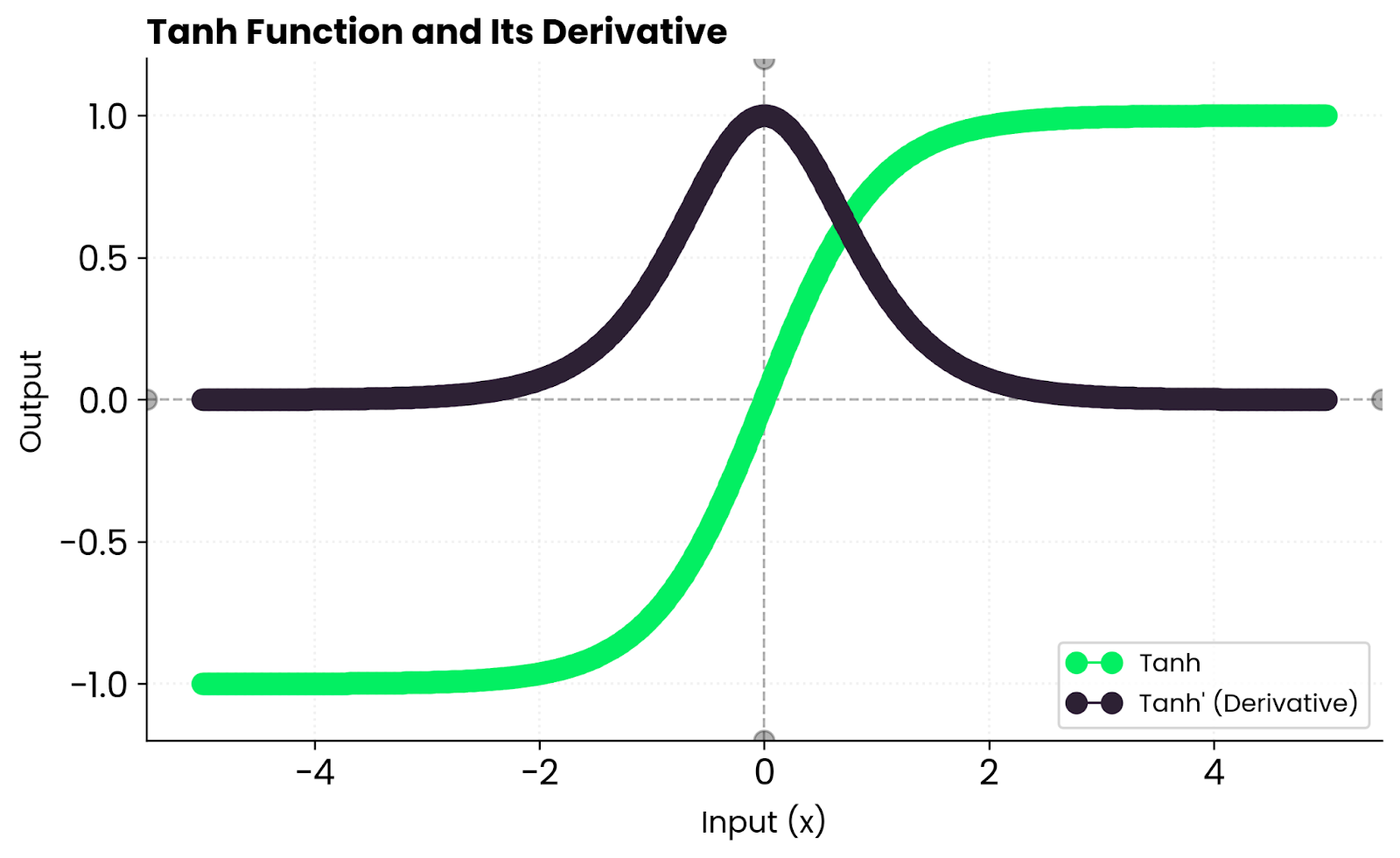
Das heißt, die Steigungen sind in der Nähe von Null ziemlich stark, werden aber zu den Rändern hin schwächer, wenn die Funktion sich sättigt. Wenn tanh(x) nahe bei 1 oder -1 liegt, geht die Ableitung gegen Null, was das Lernen für diese Neuronen verlangsamt.

In der Praxis kriegst du stabiles Lernen bei moderaten Eingaben, aber möglicherweise verschwindende Gradienten, wenn die Eingaben zu groß oder zu klein sind. Deshalb nehmen tiefe Netzwerke oft ReLU – es wird bei positiven Werten nicht gesättigt.

Tanh gegen Andere Funktionen

Tanh ist nicht die einzige Aktivierungsfunktion, die es gibt. Wenn du weißt, wie sie im Vergleich zu anderen Alternativen abschneidet, kannst du die richtige für dein Netzwerk auswählen.

Sigmoid ist eng mit tanh verbunden.ve. Eigentlich ist tanh nur eine skalierte und verschobene Version von sigmoid:

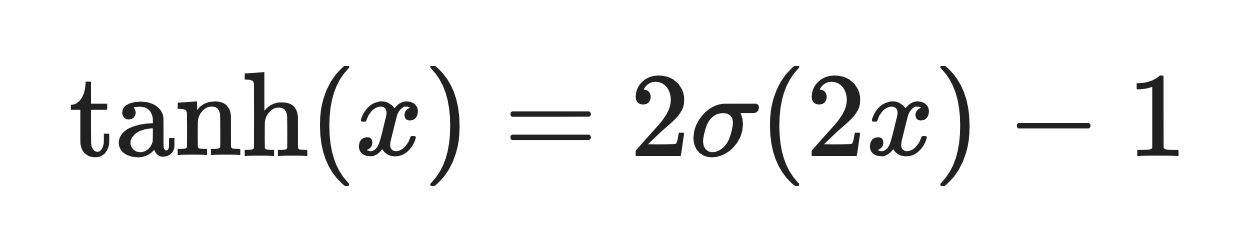
Wobei σ(x) die Sigmoid-Funktion ist.

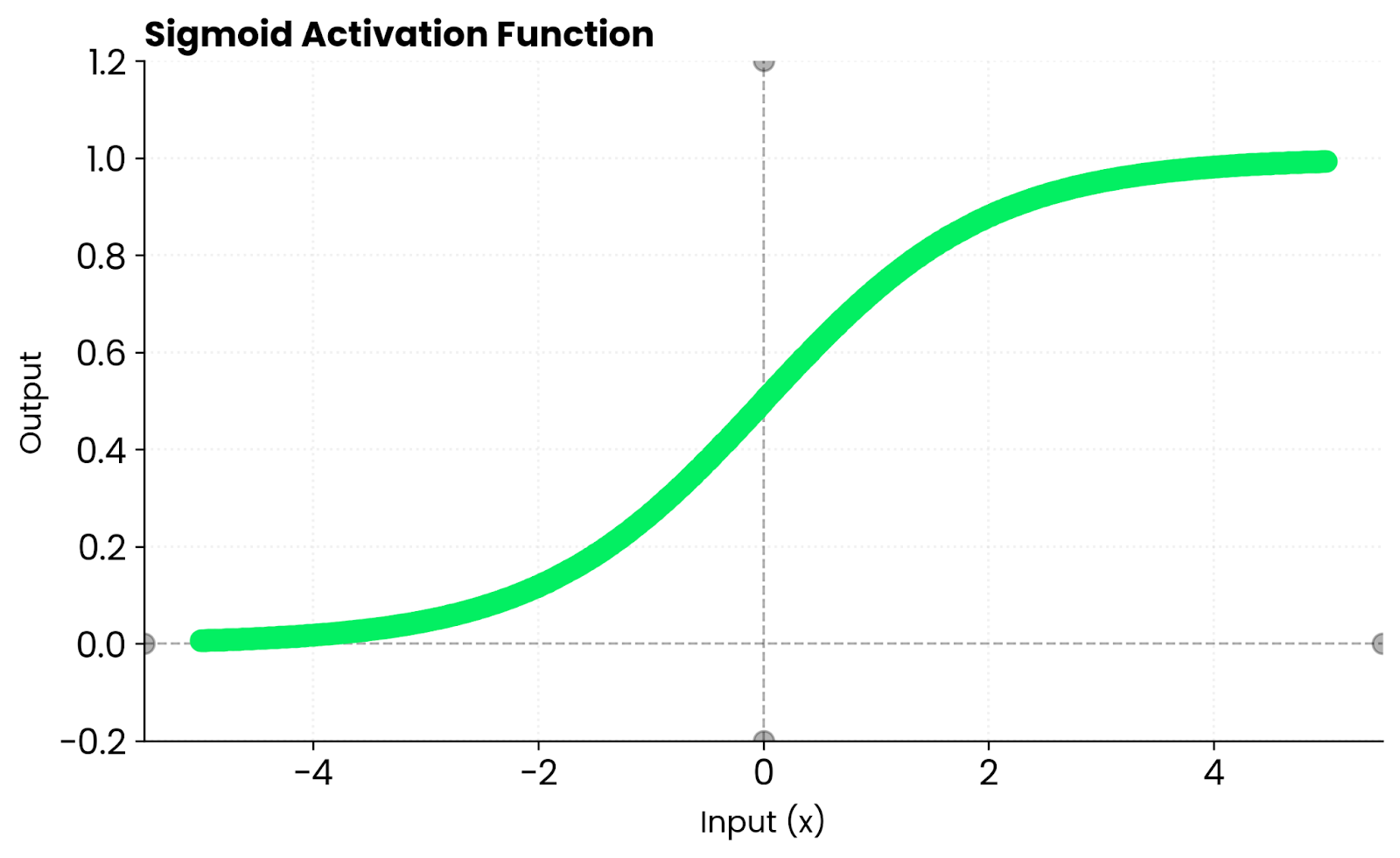
Sigmoidfunktion. Bild vom Autor

Der Hauptunterschied ist, dass Sigmoid Werte zwischen 0 und 1 gibt, während tanh Werte zwischen -1 und 1 gibt. Durch diese Nullzentrierung läuft tanh in den meisten Fällen schneller zusammen.

ReLU geht anders ran: Bei negativen Eingaben gibt's null raus und positive Eingaben bleiben so, wie sie sind. Das führt zu einer gewissen „Sparsamkeit“, was bedeutet, dass viele Neuronen inaktiv bleiben, was das Training beschleunigt. Aber ReLU macht Gradienten für negative Werte kaputt. Tanh hat dieses Problem nicht, weil es bei negativen Eingaben Gradienten ungleich Null beibehält. Es wird an beiden Enden gesättigt, was das Lernen verlangsamen kann, wenn die Eingaben zu groß oder zu klein werden.

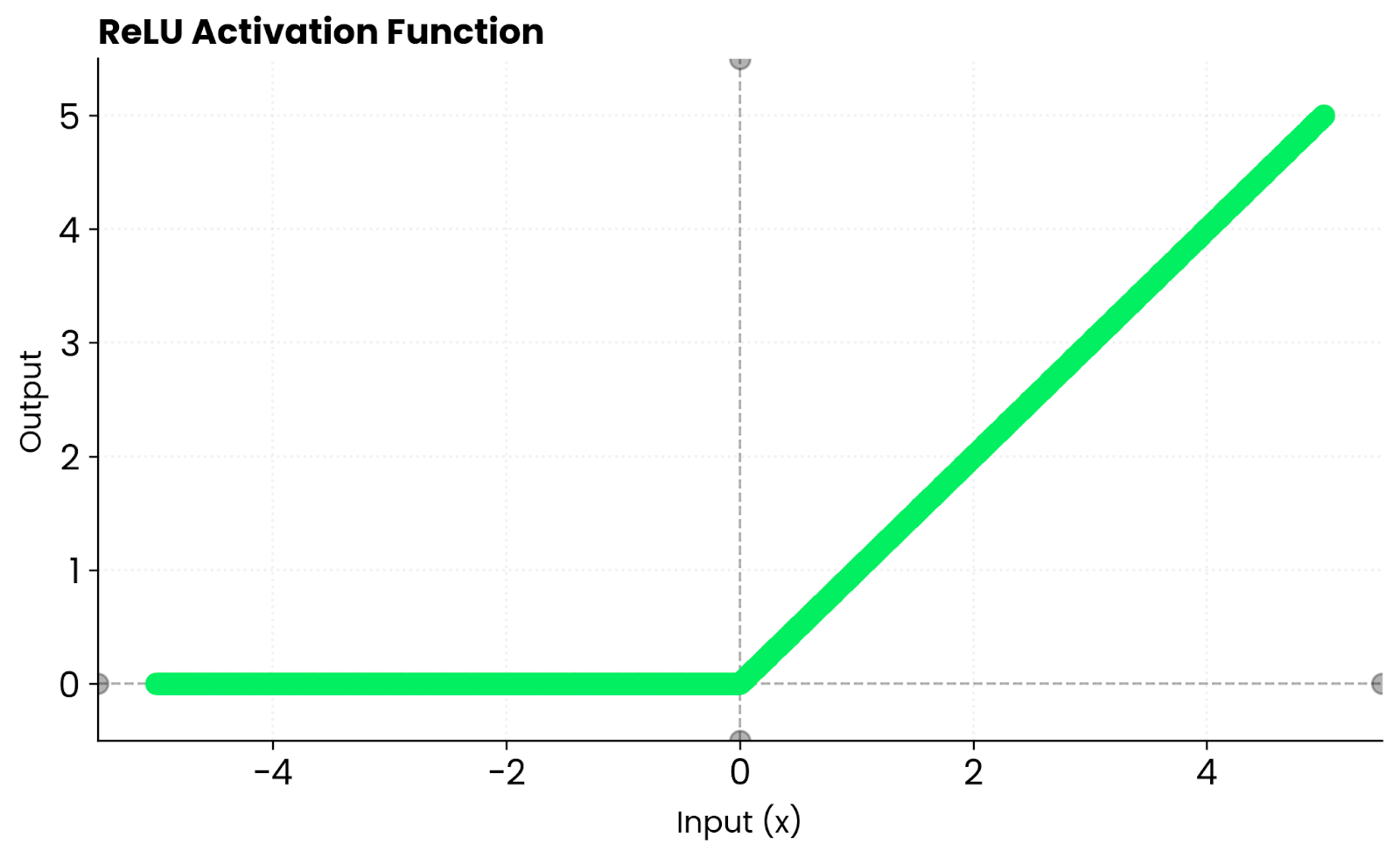
ReLU-Funktion. Bild vom Autor

Softsign sieht ähnlich aus wie tanh. Beide sind glatte, S-förmige Kurven. Aber tanh läuft schneller gegen Null, weil seine Steigung steiler ist. Das heißt, dass die Steigungen in den ersten Trainingsphasen stärker sind, was deinem Netzwerk helfen kann, schneller zu lernen, bevor die Eingaben die Sättigungszonen erreichen.

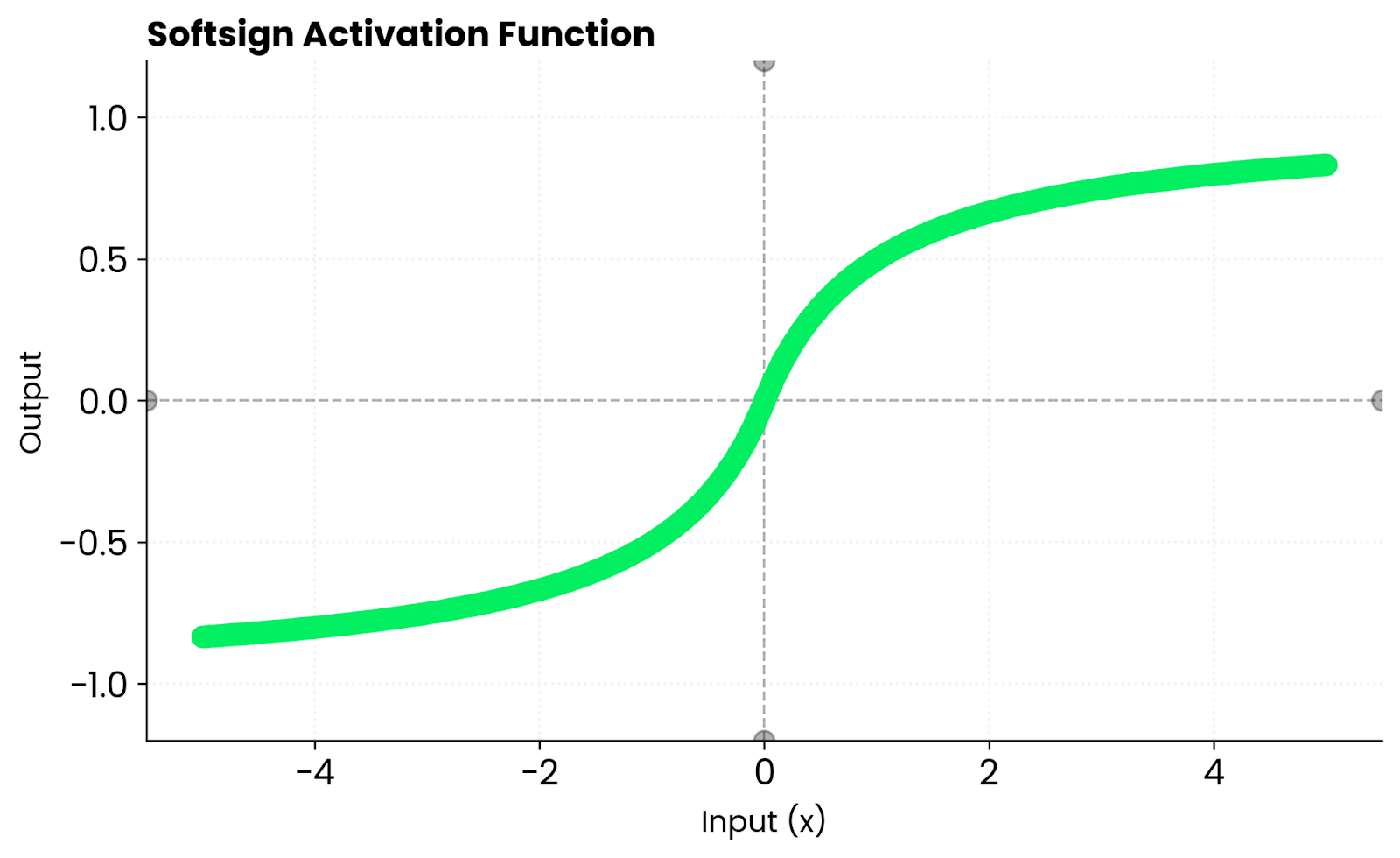
Softsign-Funktion. Bild vom Autor

Ich kratze mit diesen Aktivierungsfunktionen nur an der Oberfläche. Wenn du Alternativen zu Tanh und ReLU suchst, schau dir unseren ausführlichen Leitfaden „s to Softmax and Softplus” an.

Vorteile von Tanh

Wenn du überlegst, ob Tanh einen Versuch wert ist, findest du hier einige Vorteile, die dir am Ende vielleicht ein genaueres Bild vermitteln.

Nullzentrierte Ausgabe

Tanh gibt Werte um Null herum aus.

Das verringert Verzerrungen bei der Gewichtsaktualisierung. Wenn deine Aktivierungen um den Nullpunkt herum liegen und nicht wie bei Sigmoid positiv verzerrt sind, ziehen die Gradienten die Gewichte nicht stärker in eine Richtung als in die andere. Das Ergebnis ist eine schnellere Konvergenz und ein stabileres Training.

Stärkere Steigungen nahe Null

Tanh hat eine steile Steigung nahe Null.

Das heißt, dass die Steigungen bei der Rückpropagation stärker sind als beim Sigmoid. Dein Netzwerk lernt in den ersten Trainingsphasen schneller, wenn die meisten Aktivierungen bei fast Null liegen. Andererseits macht die sanftere Steigung von Sigmoid diese ersten Aktualisierungen schwächer und langsamer.

Gleichmäßiger Gradientenfluss

Die Ableitungen von Tanh sind überall stetig.

Es gibt keine plötzlichen Sprünge oder Unterbrechungen. Das sorgt für eine stabilere Optimierung im Vergleich zu stückweisen Funktionen wie ReLU, bei denen die Ableitung bei Null plötzlich von 0 auf 1 springt. Glatte Gradienten bedeuten vorhersehbare Gewichtsaktualisierungen während des Trainings.

Perfekt für wiederkehrende Netzwerke

RNNs, LSTMs und GRUs nutzen tanh in ihren versteckten Schichten.

Diese Architekturen müssen über alle Zeitschritte hinweg einen reibungslosen internen Zustand aufrechterhalten. Tanh lässt sowohl positive als auch negative Signale durch, während die Werte begrenzt bleiben. Diese Balance verhindert, dass es zu vielen Aktivierungen kommt, und hilft dem Netzwerk, Infos über längere Zeiträume zu behalten.

Einschränkungen und Kompromisse

Bevor ich mich mit dem Code beschäftige, möchte ich ein paar Bereiche ansprechen, in denen Tanh vielleicht nicht so gut ist.

Verschwindende Gradienten

Wenn sich die Eingaben weit von Null entfernen, nähern sich die Gradienten Null.

Das passiert, weil tanh bei -1 und 1 gesättigt ist. Sobald deine Aktivierungen diese Extreme erreichen, wird die Ableitung winzig und die Gewichtsaktualisierungen werden extrem langsam. In sehr tiefen Netzwerken wird dieses Problem noch schlimmer, weil die Gradienten kleiner werden, wenn sie durch jede Schicht zurückpropagiert werden, bis das Lernen praktisch aufhört.

Langsameres Training

Tanh macht nichts spärlich.

Jedes Neuron bleibt ein bisschen aktiv, anders als bei ReLU, wo negative Eingaben null Output bringen. Das heißt, dein Netzwerk verarbeitet mehr Infos pro Vorwärtsdurchlauf, was sich gut anhört, aber eigentlich alles verlangsamt. Die Sparsamkeit von ReLU macht das Training schneller, weil inaktive Neuronen die Berechnung komplett überspringen.

Weniger Hardware-Optimierung

Moderne Frameworks und Hardwarebeschleuniger setzen auf ReLU.

Tanh-Operationen beinhalten Exponentialfunktionen, die aufwendiger zu berechnen sind als die einfache max(0, x)-Operation von ReLU. GPU-Kernel und spezielle KI-Chips sind für ReLU optimiert, weil es in den meisten Architekturen zum Standard geworden ist. Das heißt, tanh läuft auf derselben Hardware langsamer, selbst wenn die Netzwerkarchitekturen gleich sind.

Tanh in PyTorch

PyTorch hat die Tanh-Funktion schon eingebaut, du musst sie also nicht selbst programmieren.

So benutzt man sie als Aktivierungsfunktion in einem einfachen neuronalen Netzwerk:

import torch
import torch.nn as nn

model = nn.Sequential(
    nn.Linear(10, 20),
    nn.Tanh(),
    nn.Linear(20, 1)
)

x = torch.randn(5, 10)
output = model(x)
print(output)

tensor([[ 0.0910],
               [-0.0994],
               [-0.0583],  
               [-0.2177],
               [-0.2546]], grad_fn=<AddmmBackward0>)

Du kannst tanh auch direkt auf Tensoren anwenden:

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = torch.tanh(x)
print(output)

tensor([-0.9640, -0.7616, 0.0000, 0.7616, 0.9640])

Schau mal, wie die Ausgänge um Null symmetrisch sind – negative Eingänge ergeben negative Ausgänge, und die Funktion behandelt beide Seiten gleich. Diese ausgewogene Verteilung sorgt dafür, dass dein Netzwerk während des Trainings stabil bleibt, und verhindert die Verzerrung, die man bei Funktionen wie Sigmoid sehen würde.

Wann Tanh benutzt wird

Wähle die Tanh-Funktion, wenn dein Modell von zentrierten Aktivierungen profitiert oder wenn du mit kleineren oder rekurrenten Netzwerken arbeitest.

Es ist besonders effektiv, wenn:

• Du trainierst RNNs oder LSTMs, die ausgewogene Aktivierungen brauchen. Diese Architekturen nutzen Tanh, um über Zeitabschnitte hinweg einen reibungslosen internen Zustand zu halten und gleichzeitig sowohl positive als auch negative Signale durchzulassen.
• Du modellierst kontinuierliche oder glatte Ziele. Der glatte Gradientenfluss von Tanh ist super, wenn deine Ergebnisse kontinuierlich und begrenzt sein müssen, wie zum Beispiel bei der Vorhersage von Werten, die natürlich in einen bestimmten Bereich fallen.
• Du willst stabile, differenzierbare Gradienten, brauchst aber nicht die Sparsamkeit von ReLU. Wenn dein Netzwerk nicht tief genug ist, um von ReLUs Geschwindigkeitsvorteil zu profitieren, bietet Tanh dir ein besser vorhersehbares Trainingsverhalten.

Vermeide Tanh lieber in sehr tiefen Architekturen, wo Gradientenverschwinden ein Problem sein kann. ReLU oder GELU passen da besser, weil sie bei positiven Werten nicht gesättigt sind.

Fazit

Zusammengefasst liegt die Tanh-Funktion zwischen der Einfachheit von Sigmoid und der Geschwindigkeit von ReLU.

Es ist glatt, symmetrisch und immer noch wichtig beim Deep Learning, vor allem wenn es auf ausgewogene Aktivierungen ankommt. Man findet es nicht in jeder modernen Architektur, aber es hat seine Berechtigung, wenn man zentrierte Ausgänge und einen stabilen Gradientenfluss braucht.

Wenn du dir nicht sicher bist, ob du Tanh verwenden sollst oder nicht, halte dich einfach an diese Richtlinien:

• Verwende ReLU für große, tiefe Netzwerke. Es ist schneller, läuft gut auf neuer Hardware und verhindert, dass Gradienten für positive Werte verschwinden.
• Benutz Tanh, wenn du Stabilität, Symmetrie und einen gleichmäßigeren Farbverlauf brauchst. Das heißt, man braucht wiederkehrende Netzwerke, kleinere Architekturen und Fälle, in denen nullzentrierte Aktivierungen die Konvergenz verbessern.

Mach ein paar Tests, schau dir die Ergebnisse an und lass deine Daten entscheiden, welche Aktivierung am besten zu deiner Aufgabe passt. Willst du mehr erfahren? Mach bei unserem Lernpfad „Machine Learning Scientist in Python” mit, um alles über überwachtes, unüberwachtes und Deep Learning zu lernen.