Was ist Kausale KI? Ursachen und Auswirkungen verstehen

Hast du schon einmal davon gehört, dass der Konsum von Eiscreme nach Daten aus den USA mit Hai-Angriffen in Verbindung gebracht wird?

So verrückt es auch klingen mag, diese Art von Korrelation tritt auf, wenn zwei Variablen scheinbar zusammenhängen, in Wirklichkeit aber beide von einer dritten Variable beeinflusst werden. In diesem Fall ist die Temperatur der wahrscheinliche Faktor. Im Sommer steigt der Eiskonsum wegen der Hitze. Gleichzeitig nehmen die Haiangriffe auch zu, weil mehr Menschen im Meer schwimmen.

Obwohl dieses Muster eine Korrelation in den Daten zeigt, bedeutet es nicht, dass das eine das andere verursacht. Hier kommt CausalAI ins Spiel. hilft dabei, echte Ursache-Wirkungs-Beziehungen in den Daten zu erkennen und falsche Korrelationen zu vermeiden.

In diesem Artikel werden wir das Konzept der Kausalen KI, seine Bedeutung und seine Anwendung in der Praxis untersuchen.

Was ist Kausale KI?

Kausale KI ist ein Teilgebiet der Künstlichen Intelligenz (KI), das sich mit Verstehen und Modellieren von Ursache-Wirkungs-Beziehungenund nicht nur auf das Erkennen von Mustern oder Korrelationen, wie es andere traditionelle Machine Learning Systeme tun.

Kausale KI hilft dabei, die Zuverlässigkeit, Erklärbarkeit und Robustheit von KI-Systemen zu verbessern, insbesondere in realen Szenarien wie dem Gesundheitswesen und der Wirtschaft, die von Natur aus komplexer sind.

An dieser Stelle fragst du dich vielleicht:

Warum berücksichtigen traditionelle KI-Methoden die Kausalität nicht?

Kausale KI vs. traditionelle KI: Wichtige Unterschiede

Traditionelle KI-Systeme konzentrieren sich darauf, Muster und Zusammenhänge zu erkennen und Vorhersagen auf der Grundlage von Daten zu treffen. Dabei stützen sie sich auf statistische und maschinelle Lernverfahren (ML), um Zusammenhänge in den Daten zu finden. 

Während des Trainings sind sie nämlich darauf ausgelegt, die Vorhersagegenauigkeit durch die Verwendung großer Datensätze zu optimieren. Diese Datensätze enthalten Korrelationen und die Algorithmen werden diese Korrelationen bemerken, aber explizite kausale Informationen sind möglicherweise nicht vorhanden. 

Darüber hinaus werden herkömmliche KI-Systeme oft für ihre begrenzte Erklärbarkeit kritisiert und häufig als "Black Box" bezeichnet . In diesem Zusammenhanghilft KausaleKI dabei, transparentere und interpretierbare Modelle zu erstellen, indem sie explizit über Ursachen und Wirkungen nachdenkt.

Auch wenn es für traditionelle (nicht-kausale) KI-Methoden viele Anwendungsmöglichkeiten gibt, ist die wichtigste Erkenntnis aus diesem Abschnitt:  Korrelation bedeutet nicht gleich Kausalität.

• Korrelation tritt auf, wenn sich zwei Variablen gemeinsam bewegen, aber das beweist nicht, dass die eine die andere verursacht.
• Verursachung bedeutet, dass eine Variable die andere direkt beeinflusst.

Um auf das Beispiel von Eiscreme und Haiangriffen aus der Einleitung zurückzukommen, können wir sehen, dass Eiscremeverkäufe und Haiangriffe korreliert sind (beide steigen im Sommer), aber Eiscreme verursacht keine Haiangriffe.

Grundlagen der kausalen KI

Wie wir gesehen haben, ist der Kern der Kausalen KI das Ziel, Ursache-Wirkungs-Beziehungen zwischen Variablen herzustellen. Es gibt jedoch auch zwei grundlegende Konzepte, die für das Verständnis und die Beeinflussung dieser Beziehungen innerhalb eines Systems wichtig sind:

Kontrafaktische Argumentation

Bei der kontrafaktischen Argumentation werden hypothetische Szenarien betrachtet, um zu verstehen wie Veränderungen bestimmter Variablen das Ergebnis verändern können.

Ich sehe Counterfactual Reasoning gerne als Fragen wie diese: "Was wäre passiert, wenn die Variable X einen anderen Wert angenommen hätte?". Das ist ein "Was wäre wenn" Frage.

In unserem Beispiel von Eiscreme und Hai-Attacken könnten wir uns fragen:"Was wäre, wenn der Umsatz von Eiscreme geringer gewesen wäre? Hätte es dann weniger Hai-Angriffe gegeben?"

In diesem kontrafaktischen Szenario stellen wir uns eine alternative Version der Realität vor, in der der Verkauf von Eiscreme zurückgeht, während alles andere gleich bleibt. Da sowohl der Eisverkauf als auch die Haiangriffe im Sommer aufgrund des wärmeren Wetters zunehmen (eine gemeinsame Ursache), würde eine Verringerung des Eisverkaufs die Haiangriffe nicht beeinflussen. Das zeigt eine Korrelation, keine Kausalität.

Interventionen

Interventionen beziehen sich auf die absichtliche Manipulation von Variablen innerhalb eines Systems, um Veränderungen in anderen Variablen zu beobachten. In diesem Fall besteht die Intervention darin, eine Variable aktiv auf einen bestimmten Wert zu verändern, so dass wir ihre direkten Auswirkungen auf das System untersuchen können.

In unserem Beispiel könnte eine Intervention sein: 

"Lasst uns den Eisverkauf an heißen Tagen verbieten (den Eisverkauf auf 0 setzen). Wird das die Zahl der Hai-Angriffe verringern?"

Hier ändern wir das System absichtlich, indem wir den Eisverkauf herausnehmen. Das wahrscheinlichste Ergebnis ist, dass sich die Zahl der Haiangriffe nicht ändert, da ein Verbot von Speiseeis die Menschen nicht vom Schwimmen abhält. Dieses einfache Beispiel zeigt, dass ein Eingriff in den Eisverkauf keine kausale Wirkung auf Hai-Angriffe hat.

Wenn du an grundlegenden Aspekten der Künstlichen Intelligenz interessiert bist, solltest du dir den Lernpfad KI-Grundlagen ist für dich!

Kausale KI-Modelle

In diesem Abschnitt werden wir drei kausale KI-Modelle untersuchen, die uns helfen zu verstehen, wie wir mit Kausalität arbeiten können.

Beginnen wir mit dem einfachsten Modell und gehen dann zu komplexeren Modellen über.

Gerichtet azyklische Graphen

Gerichtet azyklische Graphen (DAGs) kodieren die gerichteten Beziehungen zwischen Variablen ohne Zyklen, was bedeutet, dass es keine Schleifen gibt, in denen sich eine Variable indirekt selbst verursachen kann. Sie werden verwendet, um kausale Beziehungen auf binäre Weise darzustellen: Entweder gibt es eine Ursache-Wirkung-Beziehung zwischen zwei Variablen, dann gibt es eine gerichtete Kante von der Ursache zur Wirkung im Graphen, oder es gibt keine, und deshalb gibt es auch keine Kante.

Das DAG unseres ursprünglichen Beispiels von Eiscremekonsum und Haiangriffen zeigt zum Beispiel die folgenden Kausalpfade:

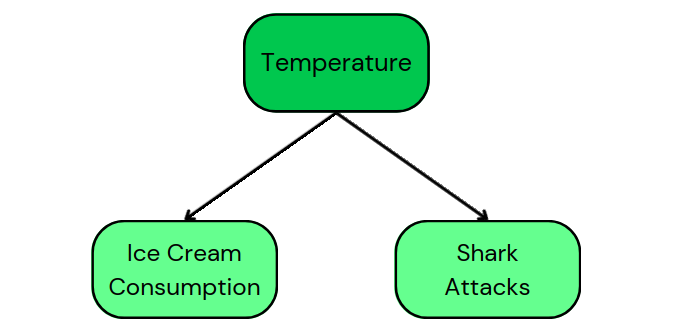
Diese DAG sagt uns, dass die Temperatur eine häufige Ursache für den Verzehr von Eiscreme und für Hai-Angriffe ist. Außerdem zeigt sie, dass es keinen kausalen Zusammenhang zwischen dem Konsum von Eiscreme und Hai-Angriffen gibt.

DAGs sind einfache Darstellungen, aber sie können komplexer werden, wenn man mehr Informationen zu den Pfaden hinzufügt, wie wir in den folgenden Abschnitten sehen werden.

Strukturelle Kausalmodelle

Strukturelle Kausalmodelle (SCMs) beinhalten Gleichungen, die modellieren, wie Variablen von anderen beeinflusst werden. Um von einem DAG zu einem SKM zu gelangen, müssen wir unter ein System von Strukturgleichungen aufstellen, die quantitativ beschreiben, wie jede Variable erzeugt wird.

Konkret ist eine Strukturgleichung in diesem Zusammenhang eine mathematische Gleichung, die eine Variable (Ergebnis) als Funktion einer oder mehrerer anderer Variablen (Ursachen) plus einem Störungsterm ausdrückt, der alle anderen Einflüsse auf dieses Ergebnis darstellt. In unserem Beispiel:

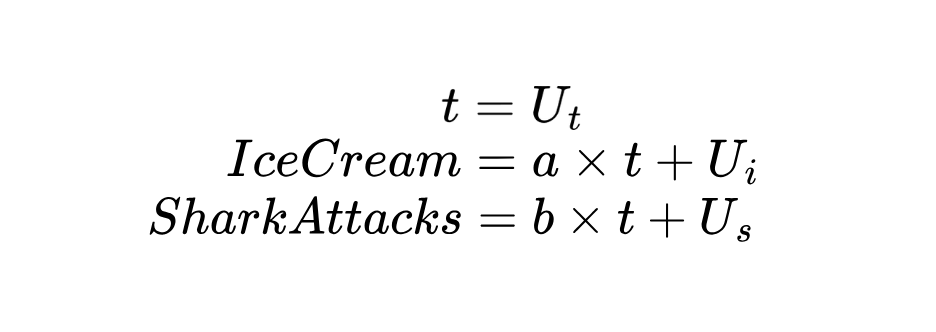
Da die Temperatur (t) eine exogene Variable ist, was bedeutet, dass sie nicht durch die beiden anderen Variablen verursacht wird, gehen wir davon aus, dass sie durch externe Faktoren bestimmt wird.

In den obigen Gleichungen folgen sowohl der Eiscremekonsum als auch die Hai-Attacken einem linearen Modell für die Temperatur, was zeigt, wie sich eine Temperaturänderung auf beide Ergebnisse auswirkt.

Wir können sogar noch einen Schritt weiter gehen und dem Spiel Wahrscheinlichkeiten hinzufügen!

Bayes'sche Netze

Bayes'sche Netze (BNs) können als eine besondere Ausprägung von SCMs betrachtet werden, bei denen die Strukturgleichungen probabilistisch ausgedrückt werden.

Ein BN verwendet die gleiche Ursache-Wirkungs-Struktur, aber anstatt exakte Formeln aufzuschreiben (wie ein lineares Modell), beschreibt es die Wahrscheinlichkeiten oder Chancen verschiedener Ergebnisse. Mit anderen Worten: Anstelle einer Gleichung drücken wir die Wahrscheinlichkeit aus, dass Y eintritt, wenn X einen bestimmten Wert hat: P(Y | X). Diese bedingte Wahrscheinlichkeit ersetzt eine feste Gleichung in einem SKM durch eine Beschreibung der Unsicherheit.

Kausaler Rückschluss

Im Kontext der Kausalen KI bezieht sich Kausal Inferenz auf die Techniken, mit denen man Ursache-Wirkungs-Beziehungen aus Daten herausfinden kann. In diesem Fall konzentrieren wir uns nicht auf die Modelle, um die Zusammenhänge zu verstehen, sondern wir beginnen bereits mit einer Reihe von Daten und wenden verschiedene Methoden an, um diese Zusammenhänge zu erkennen. Wir werden sie überprüfen, indem wir jede Methode auf unser ursprüngliches Beispiel anwenden:

Randomisierte, kontrollierte Studien

Randomisierte kontrollierte Studien (RCTs) helfen dabei, kausale Zusammenhänge zu ermitteln, indem die Teilnehmer nach dem Zufallsprinzip verschiedenen Gruppen zugewiesen werden und die Ergebnisse verglichen werden.

Zum Beispiel bei der Beantwortung unserer Frage, "Verursacht das Essen von Eiscreme mehr Haiangriffe?" würden wir die Menschen nach dem Zufallsprinzip in zwei Gruppen einteilen:

• Gruppe A: Isst Eiscreme.
• Gruppe B: Er isst kein Eis.

Dann würden wir die Hai-Angriffsraten zwischen den Gruppen vergleichen. Im Idealfall sollten wir keinen signifikanten Unterschied bei den Hai-Angriffsraten feststellen, weil der Konsum von Eiscreme keine Hai-Angriffe verursacht. Die eigentliche Ursache ist in diesem Fall wahrscheinlich die Temperatur, die in dem Experiment nicht manipuliert wurde.

Formaler ausgedrückt, würden wir sagen, dass die Randomisierung den Effekt des Eiskremkonsums isoliertDa kein kausaler Zusammenhang gefunden wird, deutet dies darauf hin, dass der Verzehr von Speiseeis keine direkte Ursache für Hai-Angriffe ist.

Propensity Score Matching

In Szenarien, in denen eine Randomisierung nicht möglich ist, können wir uns auf Beobachtungsdaten verlassen und Propensity Score Matching (PSM) anwenden.

Tatsächlich können wir in der realen Welt keine RCTs anwenden und den Eiskonsum randomisieren, weil die Menschen entscheiden, ob sie es essen oder nicht. Unter können wir jedochBeobachtungsdaten verwenden, um nach den PSM-Schrittenauf kausale Zusammenhänge zu schließen :

1. Berechne den Propensity Score: Das ist die Wahrscheinlichkeit, dass jemand Eiscreme isst, basierend auf Faktoren wie Temperatur, Alter und anderen relevanten Variablen.
2. Vergleiche Eiscreme-Esser mit Nicht-Essern die ähnliche Propensity Scores haben, d.h. sie sind vergleichbar.
3. Schätze die Hai-Angriffsraten für beide Gruppen (Eiscreme-Esser und Nicht-Esser).

Im Idealfall sollten die Hai-Angriffsraten in beiden Gruppen ähnlichsein , was darauf hindeuten würde, dass der Konsum von Eiscreme nicht die Ursache für Hai-Angriffe ist. Jeder beobachtete Unterschied ist wahrscheinlich auf andere Faktoren zurückzuführen, wie z. B. die Temperatur.

Instrumentelle Variablen

Nehmen wir an, wir vermuten, dass die Temperatur eine versteckte Variable (ein Confounder) ist, die sowohl den Eiscremekonsum als auch die Haiattacken beeinflusst. Die Instrumentalvariablen-Technik (IV) hilft, dieses Problem zu lösen, indem eine zusätzliche Variable (ein Instrument)verwendet - wie z. B. den Fahrplan des Eiswagens -, die den Eiscremekonsum beeinflusst, aber nichts mit den Hai-Angriffen zu tun hat.

Wenn der Fahrplan des Lastwagens nur den Eisverkauf und nicht das Schwimmverhalten der Menschen beeinflusst, können wir ihn als Instrument verwenden, um den kausalen Effekt des Eiskremkonsums auf Haiangriffe zu isolieren. Wenn wir die IV-Methode anwenden, würden wir wahrscheinlich feststellen, dass der Konsum von Eiscreme nach Berücksichtigung dieses Instruments keine Haiattacken verursacht und die beobachtete Korrelation auf den versteckten Störfaktor zurückzuführen ist: die Temperatur.

Wenn du dich für andere Arten von Schlussfolgerungen interessierst, solltest du dir den Artikel "Was ist Machine Learning Inference? Eine Einführung in Inferenzansätze".

Rahmenwerke für die Implementierung von Kausaler KI

In diesem Abschnitt werden wir zwei verschiedene Frameworks für die Arbeit mit kausaler KI in der Praxis mit Python untersuchen.

DoWhy Python Bibliothek

DoWhy ist ein sehr interessantes Tool, weil es einen durchgängigen Rahmen für kausale Schlussfolgerungen bietet und dabei Transparenz und Interpretierbarkeit in den Vordergrund stellt.

Es ist sehr umfangreich und bietet eine Vielzahl von Algorithmen für Effektschätzungen, Ursachenanalysen, Interventionen und Kontrafakturen. Sie ist besonders nützlich für graphenbasierte Kausalschlüsse. Ich werde nicht zu sehr ins Detail gehen, denn auf DataCamp gibt es bereits ein komplettes Tutorial zu diesem Tool: Einführung in Kausale KI mit der DoWhy-Bibliothek.

Pyro PyTorch Rahmenwerk

Pyro ist ein probabilistisches Programmierframework, dessen Schwerpunkt auf der strukturellen und Bayes'schen Modellierung liegt. Einer der wichtigsten Vorteile von Pyro ist die nahtlose Integration mit PyTorch für GPU-Beschleunigung und Deep Learning-Anwendungen.

Wenn du interessiert bist, hat Pyro eine umfangreiche Dokumentation mit vielen Beispielen zur Verfügung.

Wenn du mit der Nutzung von KI-Frameworks wie den in diesem Abschnitt besprochenen beginnen möchtest, empfehle ich dir den DataCamp-Kurs über Entwicklung von KI-Anwendungen.

Technische Umsetzung der kausalen KI

Bisher haben wir die Grundlagen der kausalen KI, die dahinter stehenden Modelle, verschiedene Ansätze für kausale Inferenz und zwei Python-Frameworks für die Arbeit damit besprochen. Trotzdem wissen wir alle, dass der Einstieg in eine neue Disziplin schwierig sein kann. Deshalb werden wir in diesem Abschnitt die fünf wichtigsten Schritte zur Umsetzung von Kausalanalyse erläutern:

1. Datenprüfung

Die Qualität der Daten, über die wir verfügen, ist von entscheidender Bedeutung, da kausale Schlussfolgerungen in hohem Maße von Daten abhängen, die das untersuchte System genau repräsentieren. Es ist wichtig zu bedenken, dass jede Art von Fehler, fehlendem Wert oder Verzerrung kausale Beziehungen verzerren kann.

Kausalschlüsse erfordern auch reichhaltige Daten, z. B. um sicherzustellen, dass alle relevanten Störfaktoren beobachtet und in die Daten aufgenommen werden, dass die Interventionen gut definiert und über die Beobachtungen hinweg konsistent sind und dass die Gruppen vergleichbar sind, wenn Techniken angewendet werden, die diese Unterteilung erfordern. 

Ein letzter Ratschlag: Wenn du deine Daten selbst auswählen kannst, sind zeitliche Daten (Zeitreihen oder Längsschnittdaten) oft sehr nützlich für den Nachweis von Kausalität, da sie helfen, die Reihenfolge der Ereignisse zu bestimmen.

2. Modellauswahl

In diesem Schritt wird ein konzeptionelles Modell erstellt, das die Beziehungen zwischen den Variablen darstellt. Werkzeuge wie DAGs oder SCMs werden an dieser Stelle oft eingesetzt, um Annahmen über Kausalität zu formalisieren.

Wir haben gesehen, dass Confounder mögliche versteckte Variablen sind, die unsere beobachteten Variablen beeinflussen könnten. Es gibt noch zwei weitere Arten von Variablen:

• Vermittler: Variablen, die auf dem Kausalpfad liegen.
• Collider: Variablen, die von zwei anderen Variablen beeinflusst werden.

Es ist interessant, diese drei Variablentypen und ihre potenziellen Wechselwirkungen während der Modellierung zu identifizieren und die Richtung der Kausalität klar zu definieren.

3. Identifizierung

Das Ziel der Identifizierung ist es, festzustellen, ob der interessierende kausale Effekt anhand der beobachteten Daten geschätzt werden kann, wenn das Modell vorliegt. Deshalb wird in diesem Schritt geprüft, ob der kausale Effekt mit Methoden der Kausalitätsinferenz wie der Variablenidentifikation identifizierbar ist.

4. Schätzung

Sobald der kausale Effekt identifiziert ist, konzentriert sich dieser Schritt auf die Quantifizierung des kausalen Effekts mithilfe statistischer Methoden. Dies ist ein guter Zeitpunkt, um z.B. Propensity Score Matching anzuwenden.

5. Widerlegung

In dieser Phase wird geprüft, ob deine kausalen Schlussfolgerungen zutreffen, indem du Annahmen in Frage stellst und alternative Erklärungen untersuchst. Zu den Methoden in diesem Schritt gehören kontrafaktische Überlegungen und Interventionen. Während kontrafaktische Studien untersuchen, ob sich das Ergebnis unter anderen Bedingungen ändern würde, testen Interventionen die Robustheit von Kausalzusammenhängen, indem sie aktiv Variablen verändern und die Auswirkungen beobachten.

Kausale KI-Anwendungen

Nachdem wir nun wissen, wie kausale KI funktioniert, wollen wir uns einige Beispiele für Bereiche ansehen, in denen wir sie anwenden können.

Ein gutes Beispiel für ein kausales KI-System in der realen Welt ist das Gesundheitswesen, wo es eingesetzt wird, um die Wirksamkeit von Behandlungen zu bestimmen , indem es z. B. die kausalen Auswirkungen medizinischer Eingriffe abschätzt. Außerdem werden kausale Zusammenhänge genutzt, um die Behandlungen an die spezifische Situation der einzelnen Patienten anzupassen.

Das Marketing ist ein weiterer Bereich, der von Causal AI profitiert. Causal AI hilft zum Beispiel dabei, die tatsächliche Wirkung von Marketingkampagnen zu messen, indem es zwischen Korrelation und Kausalität unterscheidet. Sie liefert tiefere Einblicke in die Entscheidungen der Kunden und ermöglicht so gezieltere und effektivere Marketingstrategien. Ähnlich verhält es sich mit Bereichen wie Wirtschaft, Wirtschaftund Supply Chain Management ebenfalls auf das Verständnis von Kausalität angewiesen.

Schlussgedanken

In diesem Artikel haben wir untersucht, wie kausale KI uns hilft, über einfache Korrelationen in Daten hinauszugehen und echte Ursache-Wirkungs-Beziehungen aufzudecken. Wir haben untersucht, wie gerichtete azyklische Graphen, strukturelle Kausalmodelle und Bayes'sche Netze als kausale Modellierungswerkzeuge dienen, um komplexe Systeme darzustellen und zu verstehen. 

Außerdem haben wir besprochen, wie man kausale KI auf Daten anwendet, wobei Randomized Controlled Trials und Propensity Score Matching bei der Schätzung kausaler Effekte helfen. Wenn der Verdacht besteht, dass nicht gemessene Einflüsse die Ergebnisse verfälschen, helfen Instrumentalvariablen dabei, versteckte Einflüsse zu identifizieren.

Abschließend haben wir die Schritte zur Umsetzung von kausaler KI in der Praxis skizziert, wobei wir den Schwerpunkt auf kontrafaktische Schlussfolgerungen und Interventionen als Schlüsselinstrumente in der Widerlegungsphase der Kausalanalyse gelegt haben.

Mit der Weiterentwicklung der kausalen KI wird sie eine immer wichtigere Rolle spielen nicht nur bei der Unterscheidung zwischen einfacher Korrelation und Kausalität, sondern auch bei der Nutzung von Kausalität für bessere Entscheidungen.

Wenn du mehr über kausale KI erfahren möchtest und darüber, wie sie Unternehmen hilft, bessere Entscheidungen zu treffen, dann schau dir unsere DataFramed-Folge über kausale KI in der Wirtschaft. Du kannst auch unseren Leitfaden für Praktika lesen Kausale KI mit der DoWhy-Bibliothek lesen, um ein praktisches Beispiel zu erhalten.