Empfindlichkeit und Spezifität: Ein kompletter Leitfaden

Machine-Learning-Anwender müssen sowohl die Qualität ihrer Daten als auch die Leistung ihrer Vorhersagemodelle bewerten.

Verschiedene Metriken können dabei helfen, vor allem bei binären Klassifizierungsaufgaben. Klassifizierungsaufgaben, bei denen jeder Datenpunkt einer von zwei möglichen Kategorien zugeordnet werden soll. Beispiele sind Kreditgenehmigung (genehmigen/nicht genehmigen), Malware-Klassifizierung (bösartig/nicht bösartig), Lebenslauf-Prüfung (in die engere Wahl nehmen/nicht in die engere Wahl nehmen) und Krankheitsdiagnose (ist krank/ist nicht krank). Sogar A/B-Tests sind eng miteinander verbunden und stellen im Wesentlichen die Frage: „Ist Version B besser als Version A?“ (Ja/Nein).

Genauigkeit gibt zwar schnell einen Überblick über die Leistung, kann aber wichtige Infos über die Fehler eines Modells verschleiern. Ein Kreditbetrugserkennungssystem, das jede Transaktion als legitim einstuft, könnte zum Beispiel eine Genauigkeit von 99 % erreichen, aber keinen einzigen echten Betrug erkennen. Sensitivität und Spezifität bieten genauere Einblicke und helfen dir nicht nur zu verstehen, wie oft ein Modell richtig liegt, sondern auch, welche Arten von Fehlern es macht und ob diese Fehler im Kontext akzeptabel sind.

In diesem Leitfaden erfährst du, was Sensitivität und Spezifität wirklich bedeuten, wann welche Kennzahl am besten passt, wie sie berechnet werden und wie du sie in deiner Arbeit mit klaren Beispielen aus der Praxis anwenden kannst.

Diagnostische Tests und klinische Entscheidungen

Sensitivität und Spezifität kommen ursprünglich aus der Medizin. Wenn man diese Kennzahlen durch die Brille von Diagnosetests und klinischen Entscheidungen betrachtet, werden viele der in diesem Artikel beschriebenen Konzepte klarer. Zur Veranschaulichung nehmen wir zwei Beispiele: die Erkennung von Krankheiten und Kreditkartenbetrug.

• Diagnostische Tests sind medizinische Verfahren, mit denen man eine Krankheit bestätigen oder ausschließen kann.
• Assay-Tests misst, ob eine bestimmte Substanz in einer Probe vorhanden ist.
• Klinische Entscheidungsfindung ist der Prozess, bei dem medizinische Fachkräfte Infos über einen Patienten sammeln, Diagnose- und Behandlungsmöglichkeiten abwägen und dann auf der Grundlage von Beweisen fundierte Entscheidungen treffen.

Zielgruppe

Dieser Artikel ist für Leute gedacht, die mit Daten arbeiten und statistische Inferenz und für bessere Entscheidungen genauere Metriken als nur die Genauigkeit brauchen. Diese Metriken helfen dabei, zu beurteilen, welche Arten von Fehlern ein Modell macht und ob diese Fehler im Kontext akzeptabel sind. Anwendungen sind, wie wir gesehen haben, die medizinische Diagnostik und die Betrugsaufdeckung. Andere Anwendungsbereiche sind Einbruchserkennung, Qualitätskontrolle in der Fertigung und Spam-Filterung.

Grundlegende Konzepte von Sensitivität und Spezifität

Bevor man Sensitivität und Spezifität interpretiert oder anwendet, muss man die grundlegenden Konzepte dahinter verstehen. In diesem Abschnitt geht's um die historischen Ursprünge, die wichtigsten Definitionen, Ableitungen und Berechnungen.

Geschichte

Die Begriffe Sensitivität und Spezifität kommen eigentlich aus der Biostatistik. Obwohl der Begriff schon früher in der medizinischen Literatur auftauchte, hat der Biostatistiker Jacob Yerushlamy ihn in seiner Artikel „Statistical Problems in Assessing Methods of Medical Diagnosis, with Special Reference to X-Ray Techniques” (Statistische Probleme bei der Bewertung medizinischer Diagnosemethoden unter besonderer Berücksichtigung von Röntgentechniken).

In den 1970ern wurde die Empfänger-Operationscharakteristik-Kurve (ROC-Kurve, wird später erklärt) zu einem Tool, um die Sensitivität und Spezifität in klinischen Tests zu analysieren. In den 1990ern hat das maschinelle Lernen diese Ideen übernommen. Heute werden diese Begriffe häufig im Gesundheitswesen und im maschinellen Lernen verwendet, um zu messen, wie gut Systeme echte Positive und echte Negative erkennen.

Verwechslungsmatrix

Angenommen, ein maschinelles Lernmodell wird verwendet, um betrügerische Kreditkartentransaktionen zu erkennen. Von 10.000 Transaktionen sind 9800 echt und 200 sind Betrug. 

Da wir uns hauptsächlich für Betrugsfälle interessieren, bezeichnen wir betrügerische Fälle als positiv und nicht betrügerische Fälle als negativ. (Welche Fälle als „positiv“ und welche als „negativ“ eingestuft werden, ist ein bisschen willkürlich; meistens gibt es aber eine klare Möglichkeit, die Fälle zu kennzeichnen.) 

Nachdem wir das Modell getestet und die vorhergesagten Betrugsfälle mit den echten verglichen haben, haben wir festgestellt, dass 160 Betrugsfälle richtig erkannt wurden, 9500 legitime Transaktionen richtig identifiziert wurden, 300 legitime Transaktionen fälschlicherweise als Betrug markiert wurden und 40 Betrugsfälle vom Modell übersehen wurden.

Um den Überblick zu behalten, wird normalerweise die folgende Bezeichnung benutzt. 

• Echte Positive (TP): 160 Betrugsfälle wurden richtig gemeldet.
• Echte Negativbefunde (TN): 9500 legitime Transaktionen werden richtig erkannt,
• Falsch positive Ergebnisse (FP): 300 legitime Transaktionen werden fälschlicherweise als Betrug markiert, und
• Falsch negative Ergebnisse (FN): Das Modell übersieht 40 Betrugsfälle.

Der zweite Buchstabe (P oder N) zeigt an, ob der Fall als positiv oder negativ vorhergesagt wurde, und der erste Buchstabe, ob die Vorhersage richtig (T) oder falsch (F) war. 

Ein „falsch positives Ergebnis“ bedeutet also, dass der Fall als positiv vorhergesagt wurde, diese Vorhersage aber falsch war, oder anders gesagt, dass der Fall als positiv vorhergesagt wurde, aber tatsächlich negativ war. Ebenso ist ein falsch negatives Ergebnis ein Fall, der als negativ vorhergesagt wurde, aber tatsächlich positiv ist.

Um diese Infos anzuzeigen, benutzen wir normalerweise eine „Verwechslungsmatrix, weil sie den Lernpfad des Modells aufzeichnet und anzeigt, wie oft das Modell falsche Vorhersagen mit tatsächlichen Ergebnissen verwechselt (FN, FP). Hier ein Beispiel: 

Schauen wir uns jetzt mal die Summen der Zeilen und Spalten an. Die Zeilensummen zeigen die Gesamtzahl der vorhergesagten Fälle an, die Spaltensummen die Gesamtzahl der tatsächlichen Fälle.

Was bedeuten diese Gesamtzahlen?

• Die Summe der ersten Zeile (460) ist die Gesamtzahl der vorhergesagten Betrugsfälle (TP + FP).
• Die Summe der zweiten Zeile (9540) ist die Gesamtzahl der vorhergesagten echten Fälle (FN + TN).
• Die Summe der ersten Spalte (200) zeigt die Gesamtzahl der echten Betrugsfälle (TP + FN).
• Die Summe der zweiten Spalte (9800) ist die Gesamtzahl der echten Fälle (FP + TN).
• Die Gesamtzahl (10.000) entspricht der Gesamtgröße unserer Stichprobe.

Definitionen

Die Sensitivität (auch als „True Positive Rate“ oder „Recall“ bezeichnet) zeigt, wie gut das Modell echte positive Fälle erkennt. Genauer gesagt ist die Sensitivität der Anteil der echten positiven Ergebnisse an den tatsächlichen positiven Ergebnissen, TP / (TP + FN). 

Genauso misstdie Spezifität (True Negative Rate) wie gut das Modell echte Negativfälle erkennen kann. Das ist der Anteil der echten Negativen an den tatsächlichen Negativen, TN / (FP + TN).

Aus statistischer Sicht ist die Sensitivität die Wahrscheinlichkeit, dass ein Test positiv ist, wenn der Patient die Krankheit hat, und die Spezifität ist die Wahrscheinlichkeit, dass ein Test negativ ist, wenn der Patient die Krankheit nicht hat.

Berechnung von Sensitivität und Spezifität

In unserem Betrugsfalle bedeutet Sensitivität = TP / (TP + FN) = 160/200 oder 80 %. Die Spezifität liegt bei 9500/9800, also ungefähr bei 97 %.

Der Kompromiss zwischen Sensitivität und Spezifität und die ROC-Analyse

Wenn sich die Schwellenwerte eines Modells ändern, ändern sich die Sensitivität und Spezifität oft in die entgegengesetzte Richtung. Eine höhere Empfindlichkeit verringert normalerweise die Spezifität und umgekehrt. In diesem Abschnitt schauen wir uns diesen Kompromiss genauer an und erklären, wie die Empfänger-Operations-Charakteristik (ROC)-Analyse einen visuellen und quantitativen Ansatz bietet, um die Modellleistung über verschiedene Schwellenwerte hinweg zu bewerten.

Kompromisse

Lass uns das Betrugseispiel so anpassen, dass es 20 weitere falsche Negativfälle gibt, FN = 60. Da die Gesamtzahl der echten Betrugsfälle immer noch bei 200 liegt, müssen jetzt 20 weniger echte Treffer (TP = 140) da sein. 

Die Empfindlichkeit ist von 80 % auf 140/200 = 70 % gesunken. Je mehr falsche Negativbefunde es gibt, desto weniger genau ist der Test, und umgekehrt. Das heißt, eine hohe Sensitivität zeigt an, dass es nur wenige falsche negative Ergebnisse gibt.

In der Medizin bedeutet das, dass ein Test mit hoher Spezifität die meisten Leute, die die Krankheit nicht haben, richtig erkennt. In unserem Beispiel zur Krebsvorsorge sorgt ein Test mit hoher Spezifität dafür, dass Leute, die keinen Krebs haben, nicht fälschlicherweise gesagt wird, dass sie Krebs haben. 

Das zeigt, wie man zwischen Sensitivität und Spezifität abwägt. Ein paar Leute könnten sich Sorgen machen, wenn sie erfahren, dass sie Krebs haben, obwohl das nicht stimmt. Aber diejenigen, die wirklich die Krankheit haben, werden richtig erkannt. In diesem Fall ist eine hohe Spezifität besser. In einer nicht perfekten Welt müssen wir gute Entscheidungen treffen, indem wir die Vor- und Nachteile verschiedener Optionen abwägen.

Schwellenwertdynamik

Ein diagnostischer Schwellenwert legt fest, ab wann ein Testergebnis als positiv oder negativ gilt. Es wandelt einen stufenlosen Wert, wie zum Beispiel eine Wahrscheinlichkeit, in einen Ja/Nein-Grenzwert um. Im Alltag entscheidet es, wo man die Grenze zwischen positiven und negativen Ergebnissen zieht.

Der Schwellenwert liegt oft bei 50 % oder 0,50. Eine Wahrscheinlichkeit von über 50 % gilt als positiv, eine Wahrscheinlichkeit von unter 50 % als negativ.

Durch das Ändern der Schwellenwerte wird festgelegt, welche Fälle als positiv und welche als negativ gelten. Diese Änderung beeinflusst das Gleichgewicht zwischen dem Erkennen echter positiver Fälle und dem Vermeiden falscher negativer Ergebnisse. 

Nimm zum Beispiel ein Modell, das die Wahrscheinlichkeit einer Krebserkrankung angibt. Wenn der Schwellenwert auf 0,3 gesetzt ist, stuft das Modell viele Leute als positiv ein. Dieser Ansatz eignet sich gut für das Screening, weil er das Risiko verringert, Fälle zu übersehen. 

Allerdings steigt dadurch das Risiko von falschen Positiven. Wenn der Schwellenwert 0,8 ist, stuft das Modell weniger Leute als positiv ein. Dieser Ansatz reduziert Fehlalarme, erhöht aber das Risiko, dass tatsächliche Fälle übersehen werden.

Wenn sich der Schwellenwert ändert, passt das Modell an, wie oft es echte Treffer findet und wie oft es falsche Treffer vermeidet. Niedrigere Schwellenwerte machen das System empfindlicher, aber weniger genau; höhere Schwellenwerte machen das System weniger empfindlich, aber genauer. 

Interpretation der ROC-Kurve

Eine Empfänger-Betriebskennlinie (ROC-Kurve) ist eine gängige grafische Darstellung, um Klassifizierungsschwellenwerte über Sensitivitäts- und Spezifitätswerte hinweg zu vergleichen. Die ROC-Kurve zeigt die Sensitivität gegen 1 - Spezifität. Jeder Punkt auf der Kurve steht für einen bestimmten Schwellenwert. Wenn sich der Schwellenwert ändert, passen sich die Sensitivität und Spezifität des Modells entsprechend an und folgen der ROC-Kurve. 

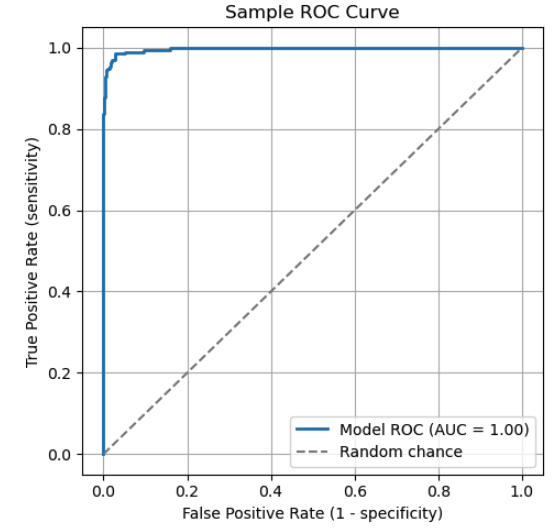
Die ROC-Kurve zeigt, wie Sensitivität und Spezifität zusammenhängen. Wichtige Punkte auf der Kurve: 

• (0,1): Ein super Klassifikator, der alle echten Treffer findet, ohne was zu übersehen.
• (0,0): Ein extremes Modell, das alles negativ vorhersagt und alle positiven Fälle falsch klassifiziert.
• (1,1): Ein extremes Modell, das alles als positiv vorhersagt und alle negativen Fälle falsch klassifiziert.

Die diagonale gestrichelte Linie steht für Zufall. Ein Modell, das so funktioniert, hat keine wirkliche Unterscheidungskraft. 

Um ein Modell mit einer ROC-Kurve zu checken, schau dir die „Fläche unter der Kurve“ (AUC) an. Der AUC ist die Gesamtfläche (Integral) unter der Kurve, die einen gewichteten Durchschnitt der Leistung über alle Schwellenwerte hinweg darstellt. Ein höherer AUC-Wert zeigt, dass positive und negative Klassen insgesamt besser voneinander unterschieden werden können.

Vorhersagewerte und Wahrscheinlichkeitsverhältnisse

In diesem Abschnitt schauen wir uns an, wie die Häufigkeit die Zuverlässigkeit von Testergebnissen beeinflusst. Wir schauen uns auch an, wie Wahrscheinlichkeitsverhältnisse Sensitivität und Spezifität in einer einzigen Zahl zusammenfassen, damit Ärzte die Diagnosewahrscheinlichkeit nach Tests anpassen können. 

Prävalenzabhängige Kennzahlen

Der positive prädiktive Wert (PPV) ist wie die Genauigkeit beim maschinellen Lernen und zeigt, wie wahrscheinlich es ist, dass eine positive Vorhersage stimmt. Es misst den Anteil der vorhergesagten positiven Ergebnisse, die auch wirklich positiv sind: PPV = TP / (TP + FP). 

Der negative prädiktive Wert (NPV) zeigt, wie zuverlässig ein negatives Ergebnis ist. Es misst den Anteil der negativen Testergebnisse, die auch wirklich negativ sind. Die Formel dafür ist NPV = TN / (TN + FN).

Nehmen wir mal an, wir testen 1000 Leute mit dieser Verwechslungsmatrix auf eine Krankheit.

• PPV = TP / (TP + FP) = 80/100 = 80%.
• NPV = TN / (FN + TN) = 890 / 900 = 98,9 %. 

Zum Vergleich nehmen wir mal an, dass mehr Leute krank sind (300 statt 90) und passen die Verwechslungsmatrix entsprechend an.

Mit steigender Prävalenz steigt auch die Anzahl der echten positiven Fälle. 

• Höhere PPV-. Ein positives Ergebnis spiegelt jetzt eher die tatsächliche Erkrankung wider. Tatsächlich beträgt die PPV 270 / 300 = 90 %, verglichen mit vorher 80 %, was einer Steigerung von 10 % entspricht.
• Niedrigerer Barwert. Ein negatives Ergebnis wird etwas weniger zuverlässig, weil es mehr Möglichkeiten gibt, echte Fälle zu übersehen. Wir sehen, dass der NPV = 630 / 700 = 90 % ist, was einem Rückgang von 8,9 % entspricht.

Wahrscheinlichkeitsverhältnisse

Wahrscheinlichkeitsverhältnisse kombinieren Sensitivität und Spezifität in einer einzigen Zahl, die Ärzten hilft, ihre Diagnose anhand der Testergebnisse besser einzuschätzen.

Wahrscheinlichkeit versus Chancen

Bevor man Wahrscheinlichkeitsverhältnisse anwendet, muss man zwischen Wahrscheinlichkeit und Oddsunterscheiden . Die Wahrscheinlichkeit ist die Chance, dass etwas passiert, ausgedrückt als Wert zwischen 0 und 1. Quoten zeigen, wie wahrscheinlich es ist, dass etwas passiert, im Vergleich dazu, dass es nicht passiert. 

Eine Wahrscheinlichkeit von 75 % heißt, dass das Ereignis in 75 von 100 Fällen passiert. Die entsprechendenQuoten von für dieses Ereignis sind 0,75 / (1 - 0,75) = 0,75 / 0,025 = 3. Das heißt, die Chancen stehen 3 zu 1, dass das Ereignis eintritt.

Allgemeiner gesagt: Wenn p die Wahrscheinlichkeit eines Ereignisses ist, dann ist die Wahrscheinlichkeit = p / (1 - p). Umrechnung von Quoten in Wahrscheinlichkeiten: p = Quote / (1 + Quote).

Wahrscheinlichkeitsverhältnisse

Die positive Wahrscheinlichkeitsquote (LR+) zeigt dir, um wie viel ein positives Ergebnis die Wahrscheinlichkeit erhöht, dass jemand die Erkrankung hat, im Vergleich zu jemandem, der sie nicht hat. Höhere Werte (>10) deuten darauf hin, dass der Test sehr gut geeignet ist, um die Erkrankung festzustellen. Die Formel lautet LR+ = Sensitivität / (1 - Spezifität). 

Der negative Likelihood Ratio (LR-) sagt dir, um wie viel ein negatives Ergebnis die Wahrscheinlichkeit, dass jemand die Erkrankung hat, im Vergleich zu jemandem ohne diese Erkrankung verringert. Niedrigere Werte (< 0,1) deuten darauf hin, dass der Test sehr gut geeignet ist, eine Erkrankung auszuschließen. Die Formel lautet LR- = (1 - Sensitivität) / Spezifität.

Wahrscheinlichkeit nach dem Test

Um Entscheidungen zu treffen, schauen Ärzte erst mal auf die Wahrscheinlichkeit vor dem Test, die sie anhand von Sachen wie den Symptomen und der Vorgeschichte des Patienten einschätzen. Diese Schätzung wird mit dem Wahrscheinlichkeitsverhältnis kombiniert, um die Wahrscheinlichkeit nach dem Test zu berechnen.

So geht's:

1. Beginne mit einer Vor-Test-Wahrscheinlichkeit p.
2. In Quoten umrechnen. Vorversuchswahrscheinlichkeit = p / (1 - p).
3. Wende das Wahrscheinlichkeitsverhältnis an. Wenn der Test positiv ist, multipliziere die Vor-Test-Wahrscheinlichkeit mit LR+, wenn er negativ ist, mit LR-. Post-Test-Wahrscheinlichkeit = Pre-Test-Wahrscheinlichkeit x LR.
4. Konvertiere die Post-Test-Wahrscheinlichkeiten wieder in Wahrscheinlichkeiten. Wahrscheinlichkeit nach dem Test = Chancen nach dem Test / (1 + Chancen nach dem Test).

Nehmen wir mal an, die Wahrscheinlichkeit, dass jemand krank ist, liegt bei 30 % und LR+ = 10. Wie hoch ist die Wahrscheinlichkeit nach dem Test? 

1. p = 0,3
2. Vorversuchswahrscheinlichkeit = 0,3/0,7 = 0,43. 
3. Wahrscheinlichkeit nach dem Test = 0,43 * 10 = 4,3
4. Wahrscheinlichkeit nach dem Test = 4,3 / (1 + 4,3) = 81 %.

Wir sehen, dass LR+ die Wahrscheinlichkeit und die Zuverlässigkeit einer Diagnose deutlich verändert hat.

Fortgeschrittene Methoden und Zukunftsperspektiven

Da Diagnosetests und Klassifizierungssysteme immer komplexer werden, gibt's neue Methoden, um die bisherigen Leistungsgrenzen zu sprengen. In diesem Abschnitt schauen wir uns an, wie Bayes'sche Ansätze personalisierte Entscheidungsschwellen ermöglichen und wie neue Technologien wie CRISPR-basierte Diagnostik die Grenzen der analytischen Sensitivität und Spezifität erweitern.

Bayesianische Ansätze

Die Idee, mit einer Vorannahme zu starten und diese anhand neuer Infos zu aktualisieren, ist das Herzstück der Bayesschen Statistik. Es gibt eine richtige Art, Wahrscheinlichkeiten zu überdenken, wenn neue Infos reinkommen. 

Das Bayes'sche Denken basiert auf drei Hauptkomponenten.

• Vorherige Wahrscheinlichkeit. Das ist die erste Meinung, bevor man neue Infos hat. („Die Vorhersage sagt, dass es zu 60 % regnen wird.“)
• Die Wahrscheinlichkeit. So wahrscheinlich sind die neuen Beweise, wenn die Überzeugung stimmt. („Ich habe Regen gehört, also ist die Wahrscheinlichkeit einer richtigen Vorhersage hoch.“)
• A-posteriori-Wahrscheinlichkeit. Das ist die überarbeitete Meinung, nachdem neue Beweise berücksichtigt wurden. Man findet es, indem man die vorherige Wahrscheinlichkeit mit der Wahrscheinlichkeit multipliziert. 

Das lässt sich mathematisch so ausdrücken: Bayes'schem Theorem.

P(A|B) = P(B|A) x P(A) / P(B)

wobei P(A|B) die A-posteriori-Wahrscheinlichkeit (die Wahrscheinlichkeit von A unter der Bedingung B) ist, P(B|A) die A-posteriori-Wahrscheinlichkeit (die Wahrscheinlichkeit von B unter der Bedingung, dass A wahr ist), P(A) die A-priori-Wahrscheinlichkeit und P(B) die Evidenz.

Schwellenwerte mit Bayes'schen Ansätzen optimieren

Wie wir gesehen haben, benutzen klassische Klassifizierungsmodelle oft einen festen Schwellenwert, wie zum Beispiel 0,5, um zu entscheiden, ob eine Ausgabe als positiv oder negativ gekennzeichnet werden soll. Bayesianische Ansätze hingegen ermöglichen es, diese Schwellenwerte je nach Kontext anzupassen, zum Beispiel anhand von individuellen Risikofaktoren, demografischen Merkmalen, Verhaltensmustern oder Echtzeitdaten. Dank dieser Flexibilität können Systeme Schwellenwerte dynamisch anpassen, anstatt sich auf einen statischen Schwellenwert für alle Fälle zu verlassen.

Stell dir ein Modell vor, das die Wahrscheinlichkeit einer Herzerkrankung vorhersagt. Ein traditionelles Modell könnte einen Schwellenwert von 0,5 verwenden. Patienten mit einer Wahrscheinlichkeit von über 50 % gelten als positiv, alle anderen als negativ.

Betrachten wir jetzt mal einen Bayes'schen Ansatz mit zwei hypothetischen Patienten:

• Patient A ist ein 68-jähriger Mann, der schon immer geraucht hat, in der Familie gibt's Herzkrankheiten und er hatte kürzlich Schmerzen in der Brust.
• Patient B ist ein 25-jähriger Nichtraucher ohne Symptome oder relevante Vorgeschichte.

Beide Patienten kriegen eine vom Test ermittelte Wahrscheinlichkeit von 0,45. Ein festes Schwellenwertmodell mit einem Schwellenwert von 0,5 würde beide Patienten als negativ einstufen. 

Ein Bayes'sches Modell berücksichtigt aber auch vorherige Risikoinfos und kann zusammen mit Vorhersageintervallen. Bei Patient A könnte das System die Entscheidungsschwelle senken und den Fall zur weiteren Untersuchung markieren. Bei Patient B kann der Schwellenwert beibehalten werden, und es wird keine weitere Behandlung empfohlen.

So passen Bayes'sche Methoden die Klassifizierungsschwelle an die Situation jedes Patienten an, was zu klinisch passenderen Entscheidungen führt.

Hochsensible/spezifische Assays

Eine neue Technologie, die die Grenzen der analytischen Empfindlichkeit und Spezifität erweitert, ist die CRISPR-basierte Diagnostik. CRISPR-basierte Diagnostik. Wissenschaftler haben CRISPR (Clustered Regularly Interspaced Short Palindromic Repeats), ein Tool zur Genbearbeitung, angepasst, um genetisches Material zu erkennen. Es nutzt Cas-Proteine, um bestimmte Nukleinsäuresequenzen mit hoher Empfindlichkeit zu erkennen.

CRISPR-basierte Tests werden schon für die Früherkennung von Krebs eingesetzt. Es werden tragbare Krebsdiagnosegeräte für den Einsatz in Kliniken entwickelt. Zwei wichtige Diagnose-Plattformen sind SHERLOCK und DETECTR. 

CRISPR-basierte Assays haben echt viele Vorteile. Sie sind super empfindlich und können deshalb winzige Mengen an DNA oder RNA erkennen. 

Das macht sie super, um Infektionen, Krebs oder seltene Mutationen früh zu erkennen. Außerdem sind sie super spezifisch, sodass sie auch bei sehr ähnlichen Gensequenzen unterscheiden können, um falsche positive Ergebnisse zu vermeiden. Weitere Vorteile sind schnelle Ergebnisse und günstige, tragbare Geräte. 

Diese Tests sind für viele verschiedene Anwendungen super, zum Beispiel zum Nachweis von Infektionskrankheiten, in der Krebsdiagnostik und beim Screening auf genetische Erkrankungen. Forscher können maschinelles Lernen nutzen, um das Design von Leit-RNA zu optimieren und die Diagnosegenauigkeit zu verbessern.

CRISPR-basierte Assays haben auch mit Herausforderungen zu kämpfen. Die meisten liefern nur ein binäres Ergebnis (positiv oder negativ). Standardisierung und Reproduzierbarkeit sind immer noch ein Thema, weil die Ergebnisse je nach Labor und Testbedingungen unterschiedlich ausfallen. 

Außerdem müssen diese Tests die gesetzlichen Anforderungen erfüllen, wie die Zulassung durch die FDA und CLIA, was eine umfassende Validierung, Dokumentation und Überprüfung erfordert. Und schließlich machen Probleme mit dem geistigen Eigentum die Lizenzierung kompliziert und verzögern die Vermarktung.

Fazit

Sensitivität und Spezifität sind echt wichtig bei der Bewertung von Diagnosetests und Klassifizierungsmodellen. Sie können aufschlussreicher sein als Genauigkeit, vor allem bei unausgewogenen Datensätzen oder wenn falsche positive oder falsche negative Ergebnisse unterschiedliche Kosten verursachen. Zusammen mit Tools wie Wahrscheinlichkeitsverhältnissen und ROC-Analysen helfen sie dabei, Dinge besser zu verstehen und bessere Entscheidungen zu treffen.

Willst du deine praktischen Fähigkeiten bei der Bewertung der Modellleistung verbessern? Schau dir auf jeden Fall diese DataCamp-Ressourcen an:

• Grundlagen des maschinellen Lernens in Python: Lerne grundlegende Konzepte und Techniken.
• Modellvalidierung in Python: Sammle praktische Erfahrungen mit Sensitivität, Spezifität, ROC-Kurven und vielem mehr.
• Biomedizinische Bildanalyse in Python: Probier diese Ideen direkt in der Gesundheitsdiagnostik aus.