Sensibilidad y especificidad: Una guía completa

Los profesionales del machine learning deben evaluar tanto la calidad de sus datos como el rendimiento de tus modelos predictivos.

Existen diversas métricas que pueden resultar útiles, especialmente cuando se trata de tareas de clasificación binaria tareas de clasificación, aquellas en las que se predice que cada punto de datos pertenece a una de dos categorías posibles. Algunos ejemplos son la aprobación de créditos (aprobar/no aprobar), la clasificación de malware (malicioso/no malicioso), la selección de currículos (preseleccionar/no preseleccionar) y el diagnóstico de enfermedades (tiene la enfermedad/no tiene la enfermedad). Incluso las pruebas A/B están estrechamente relacionadas, ya que básicamente plantean la pregunta «¿Es la versión B mejor que la versión A?» (sí/no).

Aunque la precisión ofrece un resumen rápido del rendimiento, puede ocultar información crucial sobre la naturaleza de los errores de un modelo. Por ejemplo, un detector de fraude crediticio que clasifique todas las transacciones como legítimas podría alcanzar una precisión del 99 %, pero no detectar ningún fraude real. La sensibilidad y la especificidad ofrecen información más detallada, lo que te ayuda a comprender no solo la frecuencia con la que un modelo es correcto, sino también qué tipos de errores comete y si esos errores son aceptables en el contexto.

En esta guía, aprenderás qué significan realmente la sensibilidad y la especificidad, cuándo es más adecuado utilizar cada métrica, cómo se calculan y cómo aplicarlas de forma práctica en tu trabajo mediante ejemplos claros y reales.

Pruebas diagnósticas y toma de decisiones clínicas

La sensibilidad y la especificidad tienen su origen en la evaluación médica. Enmarcar estas métricas desde la perspectiva de las pruebas diagnósticas y la toma de decisiones clínicas ayuda a aclarar muchos de los conceptos de este artículo. Para ilustrarlo, utilizaremos dos ejemplos prácticos: la detección de enfermedades y el fraude con tarjetas de crédito.

• Las pruebas diagnósticas se refieren a un procedimiento médico utilizado para confirmar o descartar una enfermedad.
• Las pruebas de ensayo miden si una sustancia determinada está presente en una muestra.
• La toma de decisiones clínicas es el proceso mediante el cual los profesionales sanitarios recopilan información sobre un paciente, consideran las opciones de diagnóstico y tratamiento, y toman decisiones informadas basadas en la evidencia.

Público objetivo

Este artículo está dirigido a profesionales de los datos que utilizan inferencia estadística y desean comprender métricas más matizadas que la precisión para tomar mejores decisiones. Estas métricas ayudan a evaluar qué tipos de errores comete un modelo y si esos errores son aceptables en el contexto. Las aplicaciones incluyen el diagnóstico médico y la detección de fraudes, como hemos visto. Otras aplicaciones incluyen la detección de intrusiones, el control de calidad en la fabricación y el filtrado de spam.

Conceptos fundamentales de sensibilidad y especificidad

Antes de interpretar o aplicar la sensibilidad y la especificidad, es esencial comprender los conceptos básicos que hay detrás de ellas. En esta sección, analizamos los orígenes históricos, las definiciones básicas, las derivaciones y los cálculos.

Historia

Los conceptos de sensibilidad y especificidad tienen su origen en la bioestadística. Aunque ya se utilizaba anteriormente en la literatura médica, el investigador en bioestadística Jacob Yerushlamy popularizó el término en su artículo «Problemas estadísticos en la evaluación de métodos de diagnóstico médico, con especial referencia a las técnicas de rayos X».

En la década de 1970, la curva característica operativa del receptor (ROC, por sus siglas en inglés) (que se describe más adelante) se convirtió en una herramienta para analizar visualmente la sensibilidad frente a la especificidad en las pruebas clínicas. En la década de 1990, el machine learning adaptó estos conceptos. Hoy en día, estos términos se utilizan ampliamente en el ámbito sanitario y en el machine learning para medir la capacidad de los sistemas para identificar verdaderos positivos y verdaderos negativos.

Matriz de confusión

Supongamos que se utiliza un modelo de machine learning para detectar transacciones fraudulentas con tarjetas de crédito. De una muestra de 10 000 transacciones, hay 9800 transacciones legítimas y 200 casos de fraude. 

Dado que nos interesan principalmente los casos de fraude, designaremos los casos fraudulentos como positivos y los no fraudulentos como negativos. (Los casos que se designan como «positivos» y «negativos» son algo arbitrarios; sin embargo, suele haber una forma obvia de etiquetarlos). 

Tras ejecutar el modelo y comparar los casos de fraude previstos con los casos reales, hemos constatado que se han detectado correctamente 160 casos de fraude, se han identificado correctamente 9500 transacciones legítimas, se han detectado erróneamente como fraudulentas 300 transacciones legítimas y el modelo no ha detectado 40 casos de fraude.

Para mantener todos estos datos claros, se utiliza habitualmente la siguiente nomenclatura. 

• Verdaderos positivos (VP): Se han detectado correctamente 160 casos de fraude.
• Verdaderos negativos (VN): Se identifican correctamente 9500 transacciones legítimas.
• Falsos positivos (FP): 300 transacciones legítimas se marcan incorrectamente como fraudulentas, y
• Falsos negativos (FN): El modelo no detecta 40 casos de fraude.

La segunda letra (P o N) se refiere a si se predijo que el caso era positivo o negativo, y la primera letra indica si esa predicción fue verdadera (T) o falsa (F). 

Por lo tanto, un «falso positivo» indica que se predijo que el caso era positivo y que dicha predicción era falsa o, en otras palabras, que se predijo que el caso era positivo, pero en realidad era negativo. Del mismo modo, un falso negativo es un caso que se predijo como negativo, pero que en realidad es positivo.

Para mostrar esta información, solemos utilizar una «matriz de confusión, llamada así porque realiza un seguimiento de la frecuencia con la que el modelo confunde predicciones incorrectas con resultados reales (FN, FP). Aquí tienes un ejemplo: 

Ahora, echemos un vistazo a los totales de filas y columnas. Las sumas de las filas indican el total de casos previstos y las sumas de las columnas indican el total real.

¿Qué representan estos totales?

• El total de la primera fila (460) representa el número total de casos de fraude previstos (TP + FP).
• El total de la segunda fila (9540) representa el número total de casos legítimos previstos (FN + TN).
• El total de la primera columna (200) representa el número total de casos de fraude reales (TP + FN).
• El total de la segunda columna (9800) representa el número total de casos legítimos reales (FP + TN).
• El total general (10 000) es igual al tamaño total de nuestra muestra.

Definiciones

La sensibilidad (también conocida como tasa de verdaderos positivos o recuperación) mide la capacidad del modelo para identificar correctamente los verdaderos positivos. Más precisamente, la sensibilidad es la proporción de verdaderos positivos respecto a los positivos reales, TP / (TP + FN). 

Del mismo modo, la especificidad (tasa de negativos verdaderos) mide la capacidad del modelo para identificar los negativos verdaderos. Es la proporción de verdaderos negativos respecto a los negativos reales, VN / (FP + VN).

Desde un punto de vista probabilístico, la sensibilidad es la probabilidad de que una prueba dé positivo si el paciente tiene la enfermedad, y la especificidad es la probabilidad de que una prueba dé negativo si el paciente no tiene la enfermedad.

Cálculo de la sensibilidad y la especificidad

En nuestro ejemplo de fraude, la sensibilidad = TP / (TP + FN) = 160/200, o 80 %. La especificidad es de 9500/9800, o aproximadamente del 97 %.

La relación entre sensibilidad y especificidad y el análisis ROC

A medida que cambian los umbrales del modelo, la sensibilidad y la especificidad suelen moverse en direcciones opuestas. El aumento de la sensibilidad suele reducir la especificidad, y viceversa. En esta sección, exploramos esta compensación inherente y analizamos cómo el análisis de la característica operativa del receptor (ROC) proporciona un enfoque visual y cuantitativo para evaluar el rendimiento del modelo en distintos umbrales.

Compensaciones

Modifiquemos el ejemplo de fraude para que haya 20 falsos negativos más, FN = 60. Dado que el número total de casos de fraude reales sigue siendo 200, ahora debe haber 20 verdaderos positivos menos (VP = 140). 

La sensibilidad ha disminuido del 80 % al 140/200 = 70 %. A medida que aumenta el número de falsos negativos, la sensibilidad disminuye, y viceversa. Esto significa que una alta sensibilidad indica que el número de falsos negativos es bajo.

En términos médicos, una prueba con alta especificidad identifica correctamente a la mayoría de las personas que no padecen la enfermedad. En nuestro ejemplo sobre la detección del cáncer, una prueba con una alta especificidad garantiza que a las personas que no padecen cáncer no se les diagnostique erróneamente esta enfermedad. 

Esto ilustra la relación entre sensibilidad y especificidad. Algunos pacientes pueden alarmarse cuando se les dice que tienen cáncer cuando en realidad no es así, pero las personas que realmente padecen la enfermedad son identificadas correctamente. En este caso, una alta especificidad es una mejor métrica. En un mundo imperfecto, debemos tomar decisiones adecuadas basándonos en una evaluación de las ventajas e inconvenientes de los distintos parámetros.

Dinámica de umbral

Un umbral de diagnóstico establece el valor límite que determina si el resultado de una prueba se considera positivo o negativo. Convierte un valor continuo, como una probabilidad, en un valor binario (sí/no). En términos cotidianos, determina dónde trazar la línea divisoria entre resultados positivos y negativos.

El umbral suele fijarse en el 50 %, o 0,50. Una probabilidad superior al 50 % se considera positiva, y una inferior al 50 % se considera negativa.

Cambiar los umbrales determina qué casos se consideran positivos y negativos. Este cambio afecta al equilibrio entre detectar verdaderos positivos y evitar falsos negativos. 

Por ejemplo, consideremos un modelo que genera una probabilidad de cáncer. Si el umbral se establece en 0,3, el modelo clasifica a muchas personas como positivas. Este enfoque funciona bien para la detección porque reduce la probabilidad de pasar por alto casos. 

Sin embargo, aumenta el riesgo de falsos positivos. Si el umbral es 0,8, el modelo clasifica a menos personas como positivas. Este enfoque reduce los falsos positivos, pero aumenta el riesgo de pasar por alto casos reales.

Cuando cambia el umbral, el modelo modifica la frecuencia con la que detecta los verdaderos positivos y la frecuencia con la que evita los falsos positivos. Los umbrales más bajos aumentan la sensibilidad, pero reducen la especificidad; los umbrales más altos reducen la sensibilidad, pero aumentan la especificidad. 

Interpretación de la curva ROC

Una curva característica operativa del receptor (ROC) es un gráfico común que se utiliza para comparar los umbrales de clasificación entre valores de sensibilidad y especificidad. La curva ROC grafica la sensibilidad frente a 1 - especificidad. Cada punto de la curva representa un umbral específico. A medida que cambia el umbral, la sensibilidad y la especificidad del modelo se ajustan en consecuencia, trazando la curva ROC. 

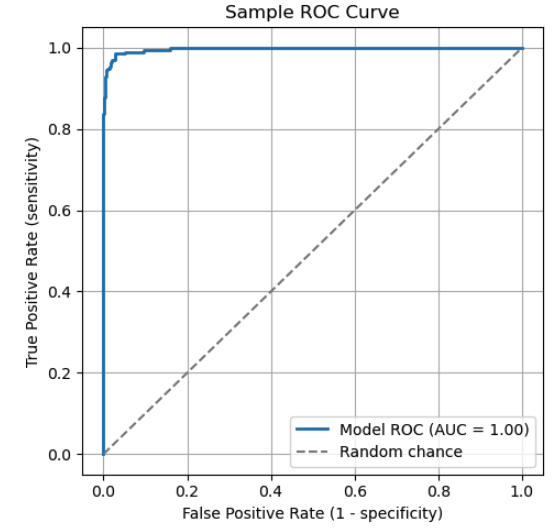
La curva ROC ilustra la relación entre sensibilidad y especificidad. Puntos clave de la curva: 

• (0,1): Un clasificador perfecto que identifica todos los verdaderos positivos sin falsos negativos.
• (0,0): Un modelo extremo que predice todo como negativo, clasificando erróneamente todos los casos positivos.
• (1,1): Un modelo extremo que predice todo como positivo, clasificando erróneamente todos los casos negativos.

La línea diagonal discontinua representa el azar. Un modelo que funciona según este principio no tiene un poder discriminatorio real. 

Para evaluar un modelo utilizando una curva ROC, ten en cuenta el «área bajo la curva» (AUC). El AUC es el área total (integral) bajo la curva, que representa un promedio ponderado del rendimiento en todos los umbrales. Un AUC más alto indica una mejor capacidad general para distinguir entre clases positivas y negativas.

Valores predictivos y razones de probabilidad

En esta sección, exploramos cómo la prevalencia influye en la fiabilidad de los resultados de las pruebas. También analizamos cómo los índices de probabilidad combinan la sensibilidad y la especificidad en un solo número que permite a los médicos actualizar las probabilidades diagnósticas después de las pruebas. 

Métricas dependientes de la prevalencia

El valor predictivo positivo (VPP), equivalente matemáticamente a la precisión en el machine learning, refleja la probabilidad de que una predicción positiva sea correcta. Mide la proporción de positivos previstos que son positivos verdaderos: PPV = TP / (TP + FP). 

El valor predictivo negativo (VPN) refleja la fiabilidad de un resultado negativo. Mide la proporción de resultados negativos que son verdaderos negativos. Su fórmula es VAN = TN / (TN + FN).

Supongamos que realizamos pruebas a 1000 personas para detectar una enfermedad con esta matriz de confusión.

• PPV = TP / (TP + FP) = 80/100 = 80 %.
• NPV = TN / (FN + TN) = 890 / 900 = 98,9 %. 

A modo de comparación, supongamos que hay más personas enfermas (300 en lugar de 90) y ajustamos la matriz de confusión en consecuencia.

A medida que aumenta la prevalencia, aumenta el número de casos verdaderos positivos. 

• PPV más alto. Ahora es más probable que un resultado positivo refleje la enfermedad real. De hecho, PPV = 270 / 300 = 90 %, en comparación con el 80 % anterior, lo que supone un aumento del 10 %.
• Menor NPV. Un resultado negativo se vuelve ligeramente menos fiable, ya que hay más posibilidades de pasar por alto casos reales. Vemos que el VAN = 630 / 700 = 90 %, lo que supone una disminución del 8,9 %.

Ratios de probabilidad

Los índices de probabilidad combinan la sensibilidad y la especificidad en un solo número que ayuda a los médicos a actualizar su confianza en un diagnóstico basado en los resultados de las pruebas.

Probabilidad frente a probabilidades

Antes de aplicar los coeficientes de verosimilitud, es importante distinguir entre probabilidad y probabilidades. La probabilidad es la posibilidad de que ocurra un evento, expresada mediante un valor entre 0 y 1. Las probabilidades representan la probabilidad de que un evento ocurra en relación con la probabilidad de que no ocurra. 

Una probabilidad del 75 % significa que el evento ocurre 75 veces de cada 100. Las probabilidades correspondientesen del evento son 0,75 / (1 - 0,75) = 0,75 / 0,025 = 3. Esto significa que las probabilidades son de 3 a 1 a favor de que el evento ocurra.

En términos más generales, si p es la probabilidad de que se produzca un evento, entonces la probabilidad = p / (1 - p). Convirtiendo probabilidades en probabilidades, p = probabilidades / (1 + probabilidades).

Ratios de probabilidad

El índice de probabilidad positiva (LR+) indica en qué medida un resultado positivo aumenta las probabilidades de padecer la enfermedad en comparación con alguien que no la padece. Los valores más altos (>10) sugieren que la prueba es muy eficaz para descartar la afección. La fórmula es LR+ = Sensibilidad / (1 - Especificidad). 

El índice de probabilidad negativa (LR-) indica en qué medida un resultado negativo reduce las probabilidades de padecer la enfermedad en comparación con alguien que no la padece. Los valores más bajos (< 0,1) sugieren que la prueba es muy eficaz para descartar una afección. La fórmula es LR- = (1 - Sensibilidad) / Especificidad.

Probabilidad posterior a la prueba

Para tomar decisiones, los médicos comienzan con una probabilidad previa a la prueba estimada en función de factores como los síntomas y el historial del paciente. Esta estimación se combina con la razón de verosimilitud para calcular la probabilidad posterior a la prueba.

El procedimiento es el siguiente.

1. Comienza con una probabilidad previa al test p.
2. Convertir a probabilidades. Probabilidad previa a la prueba = p / (1 - p).
3. Aplica la razón de verosimilitud. Si la prueba es positiva, multiplica las probabilidades previas a la prueba por LR+, si es negativa, multiplica por LR-. Probabilidad posterior a la prueba = probabilidad previa a la prueba x LR.
4. Convierte las probabilidades posteriores a la prueba en probabilidades. Probabilidad posterior a la prueba = Probabilidad posterior a la prueba / (1 + probabilidad posterior a la prueba).

Por ejemplo, supongamos que la probabilidad previa al test de padecer la enfermedad es del 30 % y LR+ = 10. ¿Cuál es la probabilidad posterior a la prueba? 

1. p = 0,3
2. Probabilidad previa a la prueba = 0,3/0,7 = 0,43. 
3. Probabilidad posterior a la prueba = 0,43 * 10 = 4,3
4. Probabilidad posterior a la prueba = 4,3 / (1 + 4,3) = 81 %.

Observamos que LR+ modificó significativamente la probabilidad y la confianza en un diagnóstico.

Metodologías avanzadas y orientaciones futuras

A medida que las pruebas de diagnóstico y los sistemas de clasificación se vuelven más complejos, surgen nuevas metodologías para superar los límites tradicionales del rendimiento. En esta sección, exploramos cómo los enfoques bayesianos permiten establecer umbrales de decisión personalizados y cómo tecnologías novedosas, como los diagnósticos basados en CRISPR, están ampliando las fronteras de la sensibilidad y la especificidad analíticas.

enfoques bayesianos

La idea de partir de una creencia previa y actualizarla en función de la información nueva es la base de la estadística bayesiana. Proporciona una forma formal de revisar las probabilidades a la luz de nuevos datos. 

El razonamiento bayesiano se basa en tres componentes clave.

• Probabilidad previa. Esta es la creencia inicial antes de ver nuevas pruebas. («El pronóstico dice que hay un 60 % de riesgo de lluvia»).
• La probabilidad. Esta es la probabilidad de que la nueva evidencia sea cierta si la creencia es correcta. («He oído llover, por lo que la probabilidad de que el pronóstico sea correcto es alta»).
• Probabilidad posterior. Esta es la creencia revisada tras considerar nuevas pruebas. Se calcula multiplicando la probabilidad a priori por la verosimilitud. 

Esto se describe matemáticamente mediante el teorema de Bayes.

P(A|B) = P(B|A) x P(A) / P(B)

donde P(A|B) es la posterior (la probabilidad de A dado B), P(B|A) es la verosimilitud (la probabilidad de B dado que A es verdadero), P(A) es la a priori y P(B) es la evidencia.

Optimización de umbrales con enfoques bayesianos

Como hemos visto, los modelos de clasificación tradicionales suelen aplicar un umbral fijo, como 0,5, para determinar si un resultado debe etiquetarse como positivo o negativo. Los enfoques bayesianos, por el contrario, permiten que estos umbrales se adapten en función del contexto, incluyendo factores de riesgo individuales, datos demográficos, historial de comportamiento o datos en tiempo real. Esta flexibilidad permite a los sistemas ajustar los umbrales de forma dinámica, en lugar de depender de un umbral estático único para todos los casos.

Considera un modelo que predice la probabilidad de padecer una enfermedad cardíaca. Un modelo tradicional podría utilizar un umbral de 0,5. Los pacientes con una probabilidad superior al 50 % se consideran positivos, y los que están por debajo, negativos.

Ahora, consideremos un enfoque bayesiano con dos pacientes hipotéticos:

• El paciente A es un varón de 68 años, fumador habitual desde siempre, con antecedentes familiares de cardiopatías y dolor torácico reciente.
• El paciente B es un varón de 25 años, no fumador, sin síntomas ni antecedentes relevantes.

Ambos pacientes obtienen una probabilidad generada por la prueba de 0,45. Un modelo de umbral fijo con un umbral de 0,5 trataría a ambos pacientes como negativos. 

Sin embargo, un modelo bayesiano incorpora información previa sobre el riesgo y puede utilizarse junto con intervalos de predicción. En el caso del paciente A, el sistema puede reducir el umbral de decisión y marcar el caso para que se evalúe más a fondo. En el caso del paciente B, puede mantenerse el umbral y no se recomienda ningún seguimiento.

De esta forma, los métodos bayesianos adaptan el umbral de clasificación al contexto de cada paciente, lo que permite tomar decisiones más adecuadas desde el punto de vista clínico.

Ensayos de alta sensibilidad/especificidad

Una tecnología emergente que amplía los límites de la sensibilidad y la especificidad analíticas es diagnóstico basado en CRISPR. Los científicos adaptaron CRISPR (repeticiones palindrómicas cortas agrupadas y espaciadas regularmente), una herramienta de edición genética, para detectar material genético. Utiliza proteínas Cas para detectar secuencias específicas de ácido nucleico con alta sensibilidad.

Los ensayos basados en CRISPR se han utilizado para la detección precoz del cáncer. Se están desarrollando herramientas portátiles para el diagnóstico del cáncer destinadas a su uso en entornos clínicos. Dos plataformas de diagnóstico importantes son SHERLOCK y DETECTR. 

Los ensayos basados en CRISPR ofrecen muchas ventajas. Ofrecen una alta sensibilidad, por lo que pueden detectar cantidades mínimas de ADN o ARN. 

Esto los hace valiosos para identificar infecciones en fase inicial, cáncer o mutaciones raras. También ofrecen una especificidad excepcional, lo que les permite distinguir entre secuencias genéticas muy similares para reducir los falsos positivos. Entre las ventajas adicionales se incluyen resultados rápidos y un equipo portátil y económico. 

Estos ensayos admiten una amplia gama de aplicaciones, entre las que se incluyen la detección de enfermedades infecciosas, el diagnóstico del cáncer y el cribado de enfermedades genéticas. Los investigadores pueden utilizar el machine learning para optimizar el diseño del ARN guía y mejorar la precisión diagnóstica.

Los ensayos basados en CRISPR también se enfrentan a retos. La mayoría solo proporcionan un resultado binario (positivo o negativo). La estandarización y la reproducibilidad siguen siendo motivo de preocupación, ya que los resultados varían según los laboratorios y las condiciones de las pruebas. 

Además, estos ensayos deben cumplir los requisitos normativos, incluidas las aprobaciones de la FDA y la CLIA, que exigen una validación, documentación y revisión exhaustivas. Por último, las cuestiones relacionadas con la propiedad intelectual complican la concesión de licencias y ralentizan la comercialización.

Conclusión

La sensibilidad y la especificidad desempeñan un papel fundamental en la evaluación de las pruebas diagnósticas y los modelos de clasificación. Pueden ser más reveladores que la precisión, especialmente en conjuntos de datos desequilibrados o cuando los falsos positivos o los falsos negativos conllevan costes diferentes. Junto con herramientas relacionadas, como los índices de verosimilitud y el análisis ROC, guían una interpretación perspicaz y una mejor toma de decisiones.

¿Quieres profundizar tus habilidades prácticas en la evaluación del rendimiento de los modelos? Asegúrate de explorar estos recursos de DataCamp:

• Fundamentos de machine learning en Python: Aprende conceptos y técnicas fundamentales.
• Validación de modelos en Python: Adquiere experiencia práctica con la sensibilidad, la especificidad, las curvas ROC y mucho más.
• Análisis de imágenes biomédicas en Python: Aplica estos conceptos directamente en escenarios de diagnóstico sanitario.