Sensibilité et spécificité : Un guide complet

Les praticiens du machine learning doivent évaluer à la fois la qualité de leurs données et la capacité de l'algorithme à apprendre qualité de leurs données et les performances de leurs modèles prédictifs.

Divers indicateurs peuvent être utiles, en particulier lorsqu'il s'agit de tâches de classification binaire. ; celles où chaque point de données est prédit comme appartenant à l', c'est-à-dire lorsque chaque point de données est prédit comme appartenant à l'une des deux catégories possibles. Parmi les exemples, citons l'approbation de crédit (approuver/refuser), la classification des logiciels malveillants (malveillant/non malveillant), la présélection des CV (sélectionner/ne pas sélectionner) et le diagnostic médical (atteint de la maladie/non atteint de la maladie). Même tests A/B sont étroitement liés, car ils posent essentiellement la question suivante : « La version B est-elle meilleure que la version A ? » (oui/non).

Bien que la précision fournisse un résumé rapide des performances, elle peut masquer des informations cruciales sur la nature des erreurs d'un modèle. Par exemple, un détecteur de fraude à la carte de crédit qui qualifie toutes les transactions de légitimes peut atteindre une précision de 99 %, mais ne détecter aucune fraude réelle. La sensibilité et la spécificité offrent des informations plus nuancées, vous aidant à comprendre non seulement la fréquence à laquelle un modèle est correct, mais également les types d'erreurs qu'il commet et si ces erreurs sont acceptables dans le contexte.

Dans ce guide, vous apprendrez ce que signifient réellement la sensibilité et la spécificité, quand chaque indicateur est le plus approprié, comment ils sont calculés et comment les appliquer concrètement dans votre travail à l'aide d'exemples clairs et concrets.

Tests diagnostiques et prise de décision clinique

La sensibilité et la spécificité trouvent leur origine dans l'évaluation médicale. Le fait d'encadrer ces paramètres dans le contexte des tests diagnostiques et de la prise de décision clinique permet de clarifier bon nombre des concepts abordés dans cet article. Pour illustrer cela, nous allons utiliser deux exemples concrets : la détection de maladies et la fraude à la carte de crédit.

• Les tests diagnostiques désignent une procédure médicale utilisée pour confirmer ou exclure une maladie.
• Les tests d'analyse permettent de déterminer si une substance donnée est présente dans un échantillon.
• La prise de décision clinique est le processus par lequel les professionnels de santé recueillent des informations sur un patient, examinent les options diagnostiques et thérapeutiques, et prennent des décisions éclairées fondées sur des preuves.

Public visé

Cet article s'adresse aux professionnels des données qui utilisent l'l'inférence statistique et souhaitent comprendre des mesures plus nuancées que la précision afin d'améliorer leur prise de décision. Ces indicateurs permettent d'évaluer les types d'erreurs commises par un modèle et de déterminer si ces erreurs sont acceptables dans le contexte donné. Comme nous l'avons vu, les applications comprennent le diagnostic médical et la détection de fraudes. D'autres applications incluent la détection d'intrusion, le contrôle qualité dans la fabrication et le filtrage des spams.

Concepts fondamentaux de sensibilité et de spécificité

Avant d'interpréter ou d'appliquer la sensibilité et la spécificité, il est essentiel de comprendre les concepts fondamentaux qui les sous-tendent. Dans cette section, nous abordons les origines historiques, les définitions fondamentales, les dérivations et les calculs.

Historique

Les concepts de sensibilité et de spécificité trouvent leur origine dans la biostatistique. Bien qu'utilisé auparavant dans la littérature médicale, le chercheur en biostatistique Jacob Yerushlamy a popularisé le terme dans son article intitulé « Biostatistics in Cancer Treatment » (La biostatistique dans le traitement du cancer) publié dans le article « Problèmes statistiques dans l'évaluation des méthodes de diagnostic médical, avec une référence particulière aux techniques radiographiques ».

Dans les années 1970, la courbe ROC (receiver operating characteristic, caractéristique de fonctionnement du récepteur) (décrite plus loin) est devenue un outil permettant d'analyser visuellement la sensibilité par rapport à la spécificité dans les tests cliniques. Dans les années 1990, l'apprentissage automatique a adapté ces concepts. Aujourd'hui, ces termes sont largement utilisés dans les domaines de la santé et de l'apprentissage automatique pour mesurer la capacité des systèmes à identifier les vrais positifs et les vrais négatifs.

Matrice de confusion

Supposons qu'un modèle d'apprentissage automatique soit utilisé pour détecter les transactions frauduleuses par carte de crédit. Sur un échantillon de 10 000 transactions, 9 800 sont légitimes et 200 constituent des cas de fraude. 

Étant donné que nous nous intéressons principalement aux cas de fraude, désignons les cas frauduleux comme positifs et les cas non frauduleux comme négatifs. (La désignation « positif » ou « négatif » est quelque peu arbitraire ; toutefois, il existe généralement un moyen évident de classer les cas.) 

Après avoir exécuté le modèle et comparé les cas de fraude prédits aux cas réels, nous constatons que 160 cas de fraude ont été correctement signalés, 9 500 transactions légitimes ont été correctement identifiées, 300 transactions légitimes ont été signalées à tort comme frauduleuses et 40 cas de fraude n'ont pas été détectés par le modèle.

Afin de clarifier toutes ces données, la nomenclature suivante est couramment utilisée. 

• s vraies positives (TP): 160 cas de fraude ont été correctement signalés,
• Vrais négatifs (TN) : 9 500 transactions légitimes sont correctement identifiées,
• s de faux positifs (FP): 300 transactions légitimes sont signalées à tort comme frauduleuses, et
• Faux négatifs (FN): Le modèle n'a pas détecté 40 cas de fraude.

La deuxième lettre (P ou N) indique si le cas était prévu comme positif ou négatif, et la première lettre indique si cette prédiction était vraie (T) ou fausse (F). 

Ainsi, un « faux positif » indique que le cas a été prédit comme positif, mais que cette prédiction était erronée, ou en d'autres termes, que le cas a été prédit comme positif, mais qu'il était en réalité négatif. De même, un faux négatif est un cas qui a été prédit comme négatif, mais qui est en réalité positif.

Pour afficher ces informations, nous utilisons généralement une «matrice de confusion», ainsi nommée parce qu'elle suit le nombre de fois où le modèle confond des prédictions incorrectes avec des résultats réels (FN, FP). Voici un exemple : 

Maintenant, examinons les totaux des lignes et des colonnes. Les totaux des lignes indiquent le nombre total de cas prévus et les totaux des colonnes indiquent le nombre total de cas réels.

Que représentent ces totaux ?

• Le total de la première ligne (460) représente le nombre total de cas de fraude prédits (TP + FP).
• Le total de la deuxième ligne (9540) représente le nombre total de cas légitimes prédits (FN + TN).
• Le total de la première colonne (200) représente le nombre total de cas de fraude réels (TP + FN).
• Le total de la deuxième colonne (9800) représente le nombre total de cas légitimes réels (FP + TN).
• Le total général (10 000) correspond à la taille totale de notre échantillon.

Définitions

La sensibilité (également appelée taux de vrais positifs ou rappel) mesure la capacité du modèle à identifier correctement les vrais positifs. Plus précisément, la sensibilité est la proportion de vrais positifs par rapport au nombre total de positifs, TP / (TP + FN). 

De même, la spécificité (du taux de vrais négatifs) mesure la capacité du modèle à identifier les vrais négatifs. Il s'agit de la proportion de vrais négatifs par rapport aux négatifs réels, TN / (FP + TN).

D'un point de vue probabiliste, la sensibilité est la probabilité d'un test positif lorsque le patient est atteint de la maladie, et la spécificité est la probabilité d'un test négatif lorsque le patient n'est pas atteint de la maladie.

Calcul de la sensibilité et de la spécificité

Dans notre exemple de fraude, la sensibilité = TP / (TP + FN) = 160/200, soit 80 %. La spécificité est de 9500/9800, soit environ 97 %.

Le compromis sensibilité-spécificité et l'analyse ROC

Lorsque les seuils du modèle changent, la sensibilité et la spécificité évoluent souvent dans des directions opposées. Une sensibilité accrue réduit généralement la spécificité, et inversement. Dans cette section, nous explorons ce compromis inhérent et discutons de la manière dont l'analyse des caractéristiques de fonctionnement du récepteur (ROC) fournit une approche visuelle et quantitative pour évaluer les performances du modèle à différents seuils.

Compromis

Modifions l'exemple de fraude afin qu'il y ait 20 faux négatifs supplémentaires, FN = 60. Étant donné que le nombre total de cas de fraude réels est toujours de 200, il doit désormais y avoir 20 vrais positifs en moins (TP = 140). 

La sensibilité a diminué de 80 % à 140/200 = 70 %. À mesure que le nombre de faux négatifs augmente, la sensibilité diminue, et inversement. Cela signifie qu'une sensibilité élevée indique que le nombre de faux négatifs est faible.

En termes médicaux, un test présentant une spécificité élevée identifie correctement la plupart des personnes qui ne sont pas atteintes de la maladie. Dans notre exemple de dépistage du cancer, un test présentant une spécificité élevée garantit que les personnes qui ne sont pas atteintes d'un cancer ne reçoivent pas un diagnostic erroné. 

Ceci illustre le compromis entre la sensibilité et la spécificité. Quelques patients pourraient s'alarmer lorsqu'on leur annonce qu'ils ont un cancer alors qu'ils n'en ont pas, mais les personnes qui sont réellement atteintes de la maladie sont correctement identifiées. Dans ce cas, une spécificité élevée constitue un meilleur indicateur. Dans un monde imparfait, nous devons prendre les décisions appropriées en évaluant les compromis entre les différents indicateurs.

Dynamique des seuils

Un seuil diagnostique définit la valeur limite qui détermine si un résultat de test est considéré comme positif ou négatif. Il convertit une valeur continue, telle qu'une probabilité, en une valeur binaire oui/non. En termes simples, cela permet de déterminer où se situe la limite entre des résultats positifs et négatifs.

Le seuil est souvent fixé à 50 %, soit 0,50. Une probabilité supérieure à 50 % est considérée comme positive, et une probabilité inférieure à 50 % est considérée comme négative.

La modification des seuils détermine les cas considérés comme positifs et négatifs. Ce changement affecte l'équilibre entre la détection des vrais positifs et la prévention des faux négatifs. 

Prenons l'exemple d'un modèle qui fournit une probabilité de cancer. Si le seuil est fixé à 0,3, le modèle classe de nombreuses personnes comme positives. Cette approche est efficace pour le dépistage, car elle réduit le risque de passer à côté de certains cas. 

Cependant, cela augmente le risque de faux positifs. Si le seuil est de 0,8, le modèle classe moins de personnes comme positives. Cette approche réduit les faux positifs, mais augmente le risque de passer à côté de cas réels.

Lorsque le seuil change, le modèle modifie la fréquence à laquelle il détecte les vrais positifs et évite les faux positifs. Des seuils plus bas augmentent la sensibilité mais réduisent la spécificité ; des seuils plus élevés réduisent la sensibilité mais augmentent la spécificité. 

Interprétation de la courbe ROC

Une courbe ROC (Receiver Operating Characteristic) est un graphique couramment utilisé pour comparer les seuils de classification entre différentes valeurs de sensibilité et de spécificité. La courbe ROC représente la sensibilité en fonction de 1 - la spécificité. Chaque point sur la courbe représente un seuil spécifique. À mesure que le seuil change, la sensibilité et la spécificité du modèle s'ajustent en conséquence, suivant la courbe ROC. 

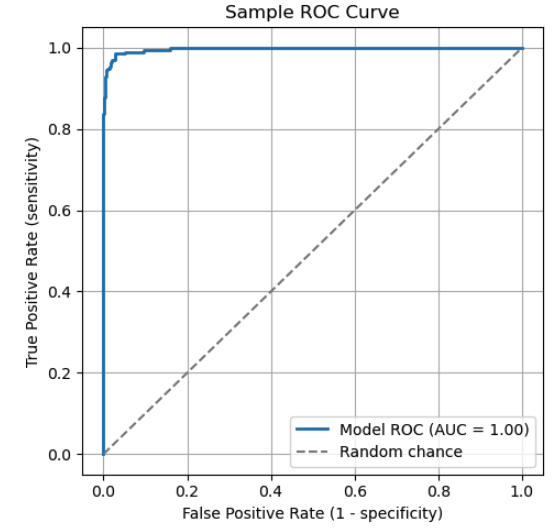
La courbe ROC illustre le compromis entre la sensibilité et la spécificité. Points clés de la courbe : 

• (0,1) : Un classificateur parfait qui identifie tous les vrais positifs sans faux négatifs.
• (0,0) : Un modèle extrême qui prédit tout comme négatif, en classant de manière erronée tous les cas positifs.
• (1,1) : Un modèle extrême qui prédit tout comme positif, en classant de manière erronée tous les cas négatifs.

La ligne pointillée diagonale représente le hasard. Un modèle qui fonctionne selon ce principe n'a pas de véritable pouvoir discriminant. 

Pour évaluer un modèle à l'aide d'une courbe ROC, examinez l'« aire sous la courbe » (AUC). L'AUC est l'aire totale (intégrale) sous la courbe, qui représente une moyenne pondérée des performances pour tous les seuils. Une AUC plus élevée indique une meilleure capacité globale à distinguer les classes positives des classes négatives.

Valeurs prédictives et rapports de vraisemblance

Dans cette section, nous examinons comment la prévalence influence la fiabilité des résultats des tests. Nous examinons également comment les rapports de vraisemblance combinent la sensibilité et la spécificité en un seul chiffre qui permet aux cliniciens de mettre à jour les probabilités diagnostiques après les tests. 

Mesures dépendantes de la prévalence

La valeur prédictive positive (VPP), mathématiquement équivalente à la précision en apprentissage automatique, reflète la probabilité qu'une prédiction positive soit correcte. Il mesure la proportion de résultats positifs prédits qui sont réellement positifs : PPV = TP / (TP + FP). 

La valeur prédictive négative (VPN) reflète la fiabilité d'un résultat négatif. Il mesure la proportion de résultats négatifs qui sont réellement négatifs. Sa formule est la suivante : VAN = VT / (VT + CF).

Supposons que nous testons 1 000 personnes pour une maladie à l'aide de cette matrice de confusion.

• PPV = TP / (TP + FP) = 80/100 = 80 %.
• NPV = TN / (FN + TN) = 890 / 900 = 98.9%. 

À titre de comparaison, supposons que davantage de personnes soient malades (300 au lieu de 90) et ajustons la matrice de confusion en conséquence.

À mesure que la prévalence augmente, le nombre de cas positifs réels augmente également. 

• s de PPV plus élevées. Un résultat positif est désormais plus susceptible de refléter la maladie réelle. En réalité, le PPV = 270 / 300 = 90 %, contre 80 % auparavant, soit une augmentation de 10 %.
• de la VAN inférieure. Un résultat négatif devient légèrement moins fiable, car il existe davantage de possibilités de passer à côté de cas réels. Nous constatons que la VAN = 630 / 700 = 90 %, soit une diminution de 8,9 %.

Ratios de vraisemblance

Les rapports de vraisemblance combinent la sensibilité et la spécificité en un seul chiffre qui aide les cliniciens à actualiser leur confiance dans un diagnostic basé sur les résultats des tests.

Probabilité et cotes

Avant d'appliquer les rapports de vraisemblance, il est important de distinguer la probabilité et la cote. La probabilité est la chance qu'un événement se produise, exprimée par une valeur comprise entre 0 et 1. Les cotes représentent la probabilité qu'un événement se produise par rapport à la probabilité qu'il ne se produise pas. 

Une probabilité de 75 % signifie que l'événement se produit 75 fois sur 100. Les cotes correspondantessur pour cet événement sont 0,75 / (1 - 0,75) = 0,75 / 0,025 = 3. Cela signifie que les chances que l'événement se produise sont de 3 contre 1.

De manière plus générale, si p est la probabilité d'un événement, alors la cote = p / (1 - p). Pour convertir les cotes en probabilités, utilisez la formule suivante : p = cote / (1 + cote).

Ratios de vraisemblance

Le rapport de vraisemblance positif (LR+) indique dans quelle mesure un résultat positif augmente les chances d'être atteint de la maladie par rapport à une personne qui n'en est pas atteinte. Des valeurs plus élevées (>10) indiquent que le test est très efficace pour confirmer la présence de la maladie. La formule est la suivante : LR+ = Sensibilité / (1 - Spécificité). 

Le rapport de vraisemblance négatif (LR-) indique dans quelle mesure un résultat négatif réduit les chances d'être atteint de la maladie par rapport à une personne qui n'en est pas atteinte. Des valeurs plus faibles (< 0,1) indiquent que le test est très efficace pour exclure une affection. La formule est LR- = (1 - Sensibilité) / Spécificité.

Probabilité post-test

Pour prendre des décisions, les cliniciens commencent par estimer la probabilité pré-test en se basant sur des facteurs tels que les symptômes et les antécédents du patient. Cette estimation est combinée avec le rapport de vraisemblance pour calculer la probabilité post-test.

La procédure est la suivante.

1. Commencez par une probabilité préalable p.
2. Convertir en cotes. Probabilité avant le test = p / (1 - p).
3. Appliquez le rapport de vraisemblance. Si le test est positif, multipliez les chances pré-test par LR+, si négatif, multipliez par LR-. Probabilité post-test = probabilité pré-test × rapport de vraisemblance.
4. Convertissez les cotes post-test en probabilités. Probabilité post-test = cote post-test / (1 + cote post-test).

Par exemple, supposons que la probabilité pré-test de la maladie soit de 30 % et que LR+ = 10. Quelle est la probabilité post-test ? 

1. p = 0,3
2. Probabilité avant le test = 0,3/0,7 = 0,43. 
3. Probabilité post-test = 0,43 * 10 = 4,3
4. Probabilité post-test = 4,3 / (1 + 4,3) = 81 %.

Nous constatons que LR+ a considérablement modifié la probabilité et la confiance dans un diagnostic.

Méthodes avancées et orientations futures

À mesure que les tests diagnostiques et les systèmes de classification deviennent plus complexes, de nouvelles méthodologies apparaissent pour dépasser les limites traditionnelles en matière de performances. Dans cette section, nous examinons comment les approches bayésiennes permettent de personnaliser les seuils de décision et comment les nouvelles technologies telles que les diagnostics basés sur CRISPR repoussent les limites de la sensibilité et de la spécificité analytiques.

approches bayésiennes

L'idée de partir d'une croyance préalable et de la mettre à jour en fonction de nouvelles informations est au cœur de la statistiques bayésiennes. Il offre un moyen formel de réviser les probabilités à la lumière de nouvelles données. 

Le raisonnement bayésien repose sur trois éléments clés.

• Probabilité a priori. Il s'agit de la croyance initiale avant d'avoir vu de nouvelles preuves. (« Les prévisions météo annoncent 60 % de risque de pluie. »)
• La probabilité. C'est la probabilité que la nouvelle preuve soit vraie si la croyance est correcte. (« J'ai entendu la pluie, donc la probabilité que la prévision soit correcte est élevée. »)
• Probabilité a posteriori. Il s'agit de la croyance révisée après examen de nouvelles preuves. Elle est obtenue en multipliant la probabilité a priori par la vraisemblance. 

Ceci est décrit mathématiquement par le théorème de Bayes. théorème de Bayes.

P(A|B) = P(B|A) x P(A) / P(B)

où P(A|B) est la probabilité a posteriori (la probabilité de A étant donné B), P(B|A) est la vraisemblance (la probabilité de B étant donné que A est vrai), P(A) est la probabilité a priori et P(B) est la preuve.

Optimisation des seuils à l'aide d'approches bayésiennes

Comme nous l'avons vu, les modèles de classification traditionnels appliquent souvent un seuil fixe, tel que 0,5, pour déterminer si une sortie doit être étiquetée positive ou négative. Les approches bayésiennes, en revanche, permettent d'adapter ces seuils en fonction du contexte, notamment des facteurs de risque individuels, des données démographiques, des antécédents comportementaux ou des données en temps réel. Cette flexibilité permet aux systèmes d'ajuster les seuils de manière dynamique, plutôt que de s'appuyer sur un seuil statique unique.

Considérons un modèle qui prédit la probabilité d'une maladie cardiaque. Un modèle traditionnel pourrait utiliser un seuil de 0,5. Les patients présentant une probabilité supérieure à 50 % sont considérés comme positifs, et ceux dont la probabilité est inférieure à 50 % sont considérés comme négatifs.

Maintenant, considérons une approche bayésienne avec deux patients hypothétiques :

• Le patient A est un homme de 68 ans, fumeur depuis toujours, présentant des antécédents familiaux de maladie cardiaque et des douleurs thoraciques récentes.
• Le patient B est un homme de 25 ans, non-fumeur, sans symptômes ni antécédents pertinents.

Les deux patients obtiennent une probabilité générée par le test de 0,45. Un modèle à seuil fixe avec un seuil de 0,5 considérerait ces deux patients comme négatifs. 

Cependant, un modèle bayésien intègre des informations préalables sur les risques et peut être utilisé conjointement avec des intervalles de prédiction. Pour le patient A, le système peut abaisser le seuil de décision et signaler le cas pour une évaluation plus approfondie. Pour le patient B, il est possible de maintenir le seuil et aucun suivi n'est recommandé.

De cette manière, les méthodes bayésiennes adaptent le seuil de classification au contexte de chaque patient, ce qui permet de prendre des décisions plus appropriées sur le plan clinique.

Tests de haute sensibilité/spécificité

Une technologie émergente qui repousse les limites de la sensibilité et de la spécificité analytiques est le diagnostic basé sur CRISPR. Les scientifiques ont adapté CRISPR (Clustered Regularly Interspaced Short Palindromic Repeats), un outil d'édition génétique, afin de détecter le matériel génétique. Il utilise des protéines Cas pour détecter des séquences d'acides nucléiques spécifiques avec une grande sensibilité.

Les tests basés sur CRISPR ont été utilisés pour la détection précoce du cancer. Des outils portables de diagnostic du cancer sont en cours de développement pour une utilisation en milieu clinique. Deux plateformes de diagnostic importantes sont SHERLOCK et DETECTR. 

Les tests basés sur CRISPR offrent de nombreux avantages. Ils offrent une grande sensibilité, ce qui leur permet de détecter des quantités infimes d'ADN ou d'ARN. 

Cela les rend précieux pour détecter les infections à un stade précoce, le cancer ou les mutations rares. Ils offrent également une spécificité exceptionnelle, leur permettant de distinguer des séquences génétiques étroitement apparentées afin de réduire les faux positifs. Parmi les autres avantages, citons des résultats rapides et un équipement portable et peu coûteux. 

Ces tests permettent une large gamme d'applications, notamment la détection de maladies infectieuses, le diagnostic du cancer et le dépistage de maladies génétiques. Les chercheurs peuvent utiliser l'apprentissage automatique pour optimiser la conception des ARN guides et améliorer la précision diagnostique.

Les tests basés sur CRISPR rencontrent également des difficultés. La plupart ne fournissent qu'un résultat binaire (positif ou négatif). La normalisation et la reproductibilité restent des préoccupations, car les résultats varient selon les laboratoires et les conditions d'essai. 

De plus, ces tests doivent satisfaire aux exigences réglementaires, notamment l'homologation par la FDA et la CLIA, qui exigent une validation, une documentation et un examen approfondis. Enfin, les questions de propriété intellectuelle compliquent l'octroi de licences et ralentissent la commercialisation.

Conclusion

La sensibilité et la spécificité jouent un rôle central dans l'évaluation des tests diagnostiques et des modèles de classification. Ils peuvent être plus pertinents que la précision, en particulier dans les ensembles de données déséquilibrés ou lorsque les faux positifs ou les faux négatifs ont des coûts différents. Associés à des outils connexes tels que les rapports de vraisemblance et l'analyse ROC, ils facilitent une interprétation pertinente et une prise de décision plus éclairée.

Souhaitez-vous approfondir vos compétences pratiques en matière d'évaluation des performances des modèles ? N'oubliez pas d'explorer ces ressources DataCamp :

• Les bases du machine learning avec Python: Apprenez les concepts et techniques fondamentaux.
• Validation de modèles en Python: Acquérez une expérience pratique en matière de sensibilité, de spécificité, de courbes ROC et bien plus encore.
• Analyse d'images biomédicales en Python: Appliquez ces concepts directement dans des scénarios de diagnostic médical.