Softplus: Die nützliche Smooth-Aktivierungsfunktion

ReLU ist seit Jahren die Standard-Aktivierungsfunktion im Deep Learning. Und dafür gibt's einen guten Grund – es ist einfach und klappt meistens gut. Aber wenn Neuronen während des Trainings anfangen, Null auszugeben, hören sie auf zu lernen, ihre Gradienten werden Null und die Rückpropagation kann ihre Gewichte nicht mehr aktualisieren. In komplexeren Netzwerken kann dieses Problem mehrere Neuronen betreffen und die Fähigkeit deines Modells beeinträchtigen, Muster in deinen Daten zu erkennen.

Einfach gesagt: Dein Netzwerk hört auf zu lernen.

Softplus bietet eine flüssige, differenzierbare Alternative, die dieses Problem löst und gleichzeitig die meisten Vorteile von ReLU beibehält. Es sieht fast so aus wie ReLU bei positiven Eingaben, aber bei negativen Werten gibt's nicht-null Gradienten. Dadurch bleiben die Neuronen während des Trainings aktiv.

In diesem Artikel erfährst du, was Softplus ist, wie es mathematisch mit ReLU verglichen werden kann und wann du es gegenüber anderen Aktivierungsfunktionen bevorzugen solltest.

Wenn du dich mit Deep Learning noch gar nicht auskennst, schau dir unseren ausführlichen Leitfaden zu Aktivierungsfunktionen in neuronalen Netzen.

Was ist die Softplus-Funktion?

Softplus ist eine glatte Aktivierungsfunktion, die wie eine differenzierbare Annäherung an ReLU funktioniert.

Die Funktion nimmt jede beliebige reelle Zahl als Eingabe und gibt einen positiven Wert aus. Softplus hat keine scharfe Ecke bei Null wie ReLU. Es geht ganz sanft durch diesen Übergangspunkt.

Hier ist die mathematische Definition:

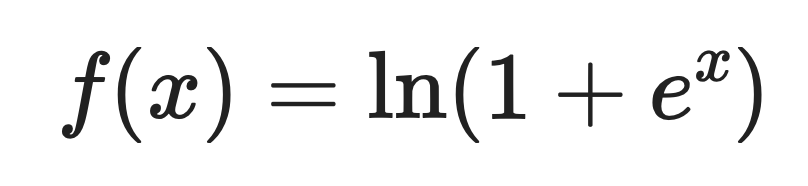
Wo:

• x ist der Eingabewert
• e ist die Eulersche Zahl (ungefähr 2,718).
• ln ist der natürliche Logarithmus.

Bei großen positiven Eingaben gibt Softplus Werte zurück, die nah an der Eingabe selbst liegen. Bei negativen Eingaben gibt es kleine positive Werte statt Null zurück.

Ableitung von Softplus

Die Ableitung von Softplus ist die logistische Sigmoidfunktion.

Das heißt:

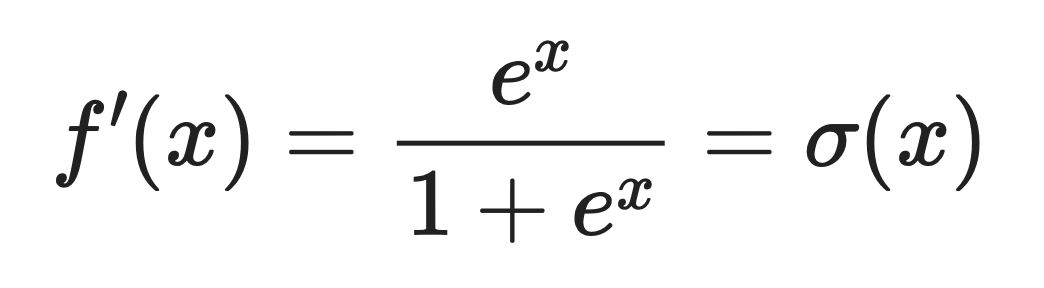
Wo σ(x) die Sigmoid-Funktion ist, die du wahrscheinlich schon mal gesehen hast.

Diese Eigenschaft macht Softplus nützlich, wenn du einen gleichmäßigen Gradientenfluss während der Rückwärtspropagierung. Die Gradienten fallen nie auf Null. Das heißt, Neuronen können ihre Gewichte immer anpassen und weiter lernen.

Verhalten in Extremsituationen

Softplus verhält sich unterschiedlich, je nachdem, ob die Eingabe groß und positiv oder groß und negativ ist.

Für große positive Werte:

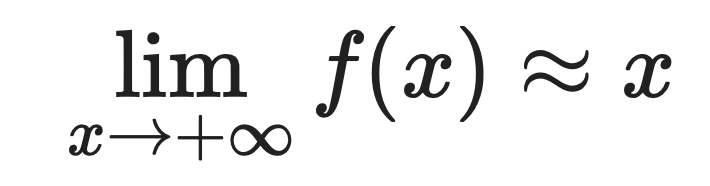
Für große negative Werte:

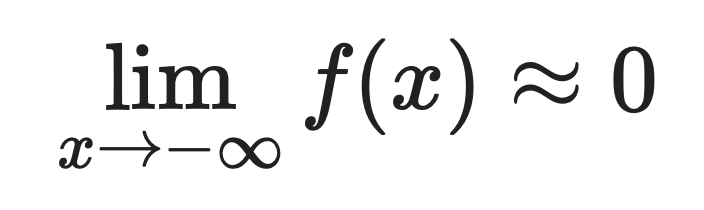
Deshalb kommt Softplus ReLU so gut nahe. Wenn x positiv und groß ist, geben beide Funktionen ungefähr den gleichen Wert zurück.

Der Unterschied ist bei negativen Eingaben zu sehen. ReLU gibt bei negativen Eingaben genau Null raus, und Softplus gibt kleine positive Werte raus.

Dieser kleine Unterschied verhindert das Problem der absterbenden Neuronen. Neuronen, die Softplus nutzen, können sich von negativen Aktivierungen erholen, weil ihre Gradienten nie ganz verschwinden.

Mathematische und rechnerische Eigenschaften

Softplus hat mathematische Eigenschaften, die du kennen solltest. Sie machen es zu mehr als nur einer glatten Version von ReLU.

Glätte und Differenzierbarkeit

Softplus ist an jedem Punkt unendlich differenzierbar.

Das heißt, du kannst die Ableitung so oft nehmen, wie du willst, und die Funktion bleibt glatt. Mathematisch gesehen ist es eine analytische Funktion.

ReLU hat dagegen einen Knick bei Null – eine scharfe Ecke, wo die Ableitung nicht existiert. Dieser nicht differenzierbare Punkt kann bei Optimierungsalgorithmen, die von glatten Gradienten ausgehen, Probleme verursachen.

Beim Deep Learning klappt die glatte Optimierung besser, wenn die Verlustfläche glatt ist. Wenn du Optimierungsmethoden zweiter Ordnung oder Algorithmen verwendest, die auf glatten Gradientenübergängen basieren, sorgt Softplus für diese Glätte.

Numerische Stabilität

Das Berechnen von Exponentialfunktionen kann zu Überlaufproblemen führen, wenn die Eingaben groß werden.

Deep-Learning-Frameworks regeln das über den Parameter „ threshold ”. Wenn der Wert diesen Schwellenwert überschreitet, wechselt die Funktion von der Berechnung des Logarithmus zur Ausgabe eines linearen Werts.

So geht's:

• Für kleine Eingaben: Softplus direkt berechnen
• Bei großen Eingaben, die den Schwellenwert überschreiten: Eingaben direkt zurücksenden

Das verhindert einen numerischen Überlauf und sorgt dafür, dass das gewünschte Verhalten erhalten bleibt. Bei großen positiven Eingaben sieht Softplus sowieso wie eine lineare Funktion aus, also hat der Schalter keinen großen Einfluss auf die Ausgabe.

Verbindung zu anderen Funktionen

Softplus hängt mit ein paar anderen Aktivierungs- und Wahrscheinlichkeitsfunktionen zusammen. So geht's:

• Sigmoid-: Wie du schon gesehen hast, ist die Ableitung von Softplus die Sigmoid-Funktion. Das heißt, Softplus ist das Integral der Sigmoidfunktion, was Sinn ergibt, wenn man sich ihre Formen anschaut.

• LogSumExp-: Softplus ist eigentlich ein Sonderfall der LogSumExp-Funktion. Für zwei Eingaben: LogSumExp(0, x) = ln(1 + e^x) = Softplus(x). Das verbindet Softplus mit numerischen Stabilitätstechniken, die beim maschinellen Lernen verwendet werden.

• Softmax: LogSumExp ist die Basis von Softmax, also hat Softplus dieselbe Herkunft. Beide Funktionen nutzen den Log-Exp-Trick für die numerische Stabilität.

• Logit-Funktion: Die Logit-Funktion ist das Gegenteil von Sigmoid. Da Sigmoid die Ableitung von Softplus ist, bilden diese drei Funktionen in der Wahrscheinlichkeitstheorie eine zusammenhängende Familie.

• Konvex konjugierte: In der konvexen Analysis ist das konvexe Konjugierte von Softplus die negative binäre Entropie. Das verbindet Softplus mit den Prinzipien der Entropiemaximierung, die in der Informationstheorie und der probabilistischen Modellierung verwendet werden.

Wenn du mit Wahrscheinlichkeitsmodellen oder Bayes'schen Frameworks arbeitest, ist Softplus wegen dieser Entropieverbindung die perfekte Wahl, um sicherzustellen, dass deine Aktivierungen mit den Prinzipien der maximalen Entropie übereinstimmen.

Vorteile von Softplus

Softplus löst bestimmte Probleme, mit denen ReLU nicht gut klarkommt. Hier sind vier davon.

Glatt und differenzierbar

Softplus ist an jedem Punkt der Kurve glatt.

Das heißt, dass die Gradienten während der Rückpropagation ohne plötzliche Sprünge oder Unterbrechungen fließen. Wenn du ein Netzwerk trainierst, sorgt ein gleichmäßiger Gradientenfluss für stabilere Gewichtsaktualisierungen und ein besseres Konvergenzverhalten.

Die scharfe Ecke von ReLU bei Null kann zu Gradientenunterbrechungen führen. Softplus hat dieses Problem nicht.

Verhindert das Absterben von Nervenzellen

Softplus gibt nie genau Null aus, auch nicht bei großen negativen Eingaben.

Das heißt, jede Nervenzelle kann weiter lernen, wie man die „ “ macht, weil die Gradienten nie ganz verschwinden. Mit ReLU kann ein Neuron, das mit der Ausgabe von Null beginnt, für immer dort hängen bleiben – sein Gradient ist Null, sodass Gewichtsaktualisierungen es nicht verschieben.

Softplus gibt dir ein Sicherheitsnetz. Neuronen können sich von negativen Aktivierungen erholen und wieder zum Netzwerk beitragen.

Die Ausgabe ist immer positiv.

Softplus sorgt dafür, dass die Ergebnisse immer positiv sind, egal was eingegeben wird.

Das ist wichtig, wenn du Modelle erstellst, die positive Vorhersagen brauchen. Poisson-Regression Modelle zählen Daten (Kunden, Ereignisse, Klicks), bei denen negative Werte keinen Sinn ergeben. Generative Modelle brauchen oft positive Ergebnisse, um Wahrscheinlichkeiten oder Intensitäten darzustellen.

Besser für bestimmte Aufgaben geeignet

Manche Aufgaben funktionieren besser, wenn sie sanft und ohne Unterbrechungen aktiviert werden.

Regressionsaufgaben mit glatten Zielfunktionen funktionieren besser mit glatten Aktivierungen. Wenn du kontinuierliche Werte wie Temperatur, Preis oder Entfernung vorhersagst, passt Softplus besser zur zugrunde liegenden Glätte deiner Daten.

Bayesianische Modelle und probabilistische Rahmenbedingungen bevorzugen auch glatte Funktionen. Wenn du Unsicherheiten modellierst oder mit Wahrscheinlichkeitsverteilungen arbeitest, machen die kontinuierlichen Ableitungen von Softplus mathematische Operationen übersichtlicher und stabiler.

Wenn du in diesen Bereichen arbeitest, bietet dir Softplus bessere theoretische Garantien und praktischere Ergebnisse als die scharfen Übergänge von ReLU.

Einschränkungen und Kompromisse

Bevor du ReLU endgültig aufgibst, solltest du ein paar Einschränkungen von Softplus kennen. Hier sind drei davon.

Höhere Rechenkosten

ReLU nutzt eine einfache Max-Operation: max(0, x).

Softplus macht Exponentialfunktionen und Logarithmen: ln(1 + e^x). Diese Vorgänge sind langsamer, vor allem wenn du sie millionenfach in großen Netzwerken mit Tausenden von Neuronen durchführst.

Der Unterschied summiert sich. Dieser Rechenaufwand kann die Trainingszeit verlängern.

Langsameres Zusammenwachsen

Softplus hat sanftere Farbverläufe, was auf dem Papier gut klingt.

Aber flüssig heißt nicht immer schnell. Die scharfen Übergänge von ReLU sorgen für spärliche Aktivierungen – viele Neuronen geben genau null aus. Diese Sparsamkeit hilft dabei, dass sich Gradienten während der Rückpropagierung schneller durch das Netzwerk ausbreiten.

Softplus hat diese Knappheit nicht. Jedes Neuron gibt einen Wert ungleich Null aus, was mehr Rechenaufwand und möglicherweise eine langsamere Konvergenz in tiefen Architekturen bedeutet.

In der Praxis eher selten

ReLU ist seit Jahren das Maß aller Dinge im Deep Learning.

Das heißt, es gibt mehr Dokumentation, Probleme/Lösungen und allgemeine Ressourcen dazu. Softplus wird nicht so behandelt. Weniger Leute nutzen es, also gibt's weniger Community-Wissen, weniger Antworten auf Stack Overflow und weniger vortrainierte Modelle, die es verwenden.

Wenn du dich für Softplus entscheidest, wählst du einen Weg, der weniger Support und möglicherweise mehr Debugging auf eigene Faust mit sich bringt.

Softplus in PyTorch

PyTorch macht Softplus einfach zu benutzen, mit eingebauter Unterstützung und zwei Parametern, die sein Verhalten steuern.

Nur zur Info, das ist die Version von PyTorch, die ich benutze:

import torch
import torch.nn as nn

print(torch.__version__)

Hier ist die grundlegende Umsetzung:

# Create a Softplus activation function
softplus = nn.Softplus(beta=1, threshold=20)

# Apply it to some input
x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
output = softplus(x)

print(output)

Ganz einfach. Aber diese beiden Parameter – beta und threshold – verändern das Verhalten der Funktion. Schauen wir uns das mal genauer an.

Der Beta-Parameter

Der Parameter „ beta “ regelt, wie glatt die Softplus-Kurve ist.

Wenn du beta erhöhst, wird die Funktion steiler und nähert sich ReLU an. Wenn du sie verringerst, wird die Funktion sanfter und allmählicher. So läuft das im Code ab:

x = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])

# Steeper activation (closer to ReLU)
softplus_steep = nn.Softplus(beta=2, threshold=20)
output_steep = softplus_steep(x)

# Smoother activation
softplus_smooth = nn.Softplus(beta=0.5, threshold=20)
output_smooth = softplus_smooth(x)

print("Softplus - Steeper activation")
print(output_steep)

print()

print("Softplus - Smoother activation")
print(output_smooth)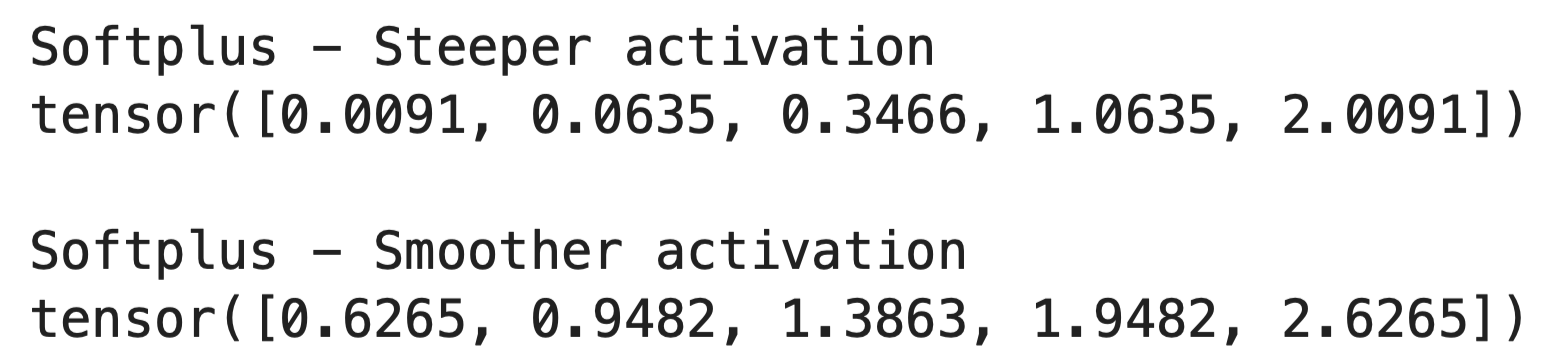

Die Standard- beta=1 -Datei funktioniert in den meisten Fällen gut. Du solltest das nur ändern, wenn du die Empfindlichkeit der Aktivierung für bestimmte Aufgaben anpassen musst.

Der Schwellenwertparameter

Der Parameter „ threshold “ verhindert einen numerischen Überlauf bei großen Eingaben.

Weißt du noch, wie die Berechnung von e^x bei großen x-Werten total aus dem Ruder laufen kann? Wenn der Input den Schwellenwert überschreitet, wechselt PyTorch von der Berechnung der vollständigen Softplus-Formel dazu, den Input direkt zurückzugeben:

softplus = nn.Softplus(beta=1, threshold=20)

# Large input bypasses the exponential
large_input = torch.tensor([25.0])
print(softplus(large_input))

Die Standard- threshold=20 -Datei klappt in den meisten Fällen. An dieser Stelle ist Softplus sowieso schon fast eine lineare Funktion, also hat der Wechsel keinen Einfluss auf die Ergebnisse.

Wann sollte man Softplus verwenden?

Wähle Softplus, wenn du eine glatte Farbverlaufsoptimierungbrauchst . Wenn du Optimierungsmethoden oder Algorithmen zweiter Ordnung verwendest, die glatte Verlustflächen voraussetzen, liefert Softplus dir die kontinuierlichen Ableitungen, auf denen diese Methoden basieren.

Benutz das, wenn dein Modell nicht-negative Ausgängebraucht . Zähldaten, Intensitätswerte und Wahrscheinlichkeitsparameter müssen alle positiv bleiben. Softplus macht das ganz einfach, ohne dass man sich extra was einfallen lassen muss.

Flache Netzwerke profitieren mehr von Softplus als tiefe Netzwerke. Wenn du nur wenige Schichten hast, beeinträchtigt schon der Verlust eines einzigen Neurons durch das ReLU-Problem die Leistung. Softplus hält alle Neuronen am Laufen und sorgt dafür, dass sie weiter lernen.

Du kannst auch Softplus für Wahrscheinlichkeitsmodelle und Bayes'sche Frameworkswählen . Die sanften Übergänge und Entropieverbindungen machen die mathematischen Operationen übersichtlicher. Energiebasierte Modelle profitieren auch davon, dass Softplus immer weiterentwickelt wird.

Modelle, bei denen du kontinuierliche Gradienten interpretierenmusst , funktionieren besser mit Softplus. Wenn du analysierst, wie dein Netzwerk auf Eingabeänderungen reagiert, oder den Gradientenfluss untersuchst, geben dir die glatten Ableitungen klarere Einblicke als die scharfen Übergänge von ReLU.

Wenn ReLU immer noch besser ist

Wechsle nicht zu Softplus, nur weil es auf dem Papier besser klingt oder weil es etwas Neues und Glänzendes ist.

• Große, tiefe Netzwerke trainieren mit ReLU schneller. Der Rechenaufwand von Softplus summiert sich über Hunderte von Schichten und Millionen von Parametern. Die Sparsamkeit von ReLU hilft auch beim Speicher und bei der Geschwindigkeit.
• Produktionssysteme setzen oft auf ReLU, weil Hardware-Optimierungen speziell darauf ausgerichtet sind. Dein Training könnte mit Softplus auf derselben Hardware um 10 bis 20 % langsamer sein.
• Normale Computer-Vision- und NLP-Aufgaben profitieren normalerweise nicht von Softplus. Die Community hat jahrelang daran gearbeitet, die Architekturen rund um ReLU zu optimieren, und wenn man die Aktivierungsfunktionen ändert, muss man dieses Wissen neu aufbauen.

Für die meisten Projekte solltest du mit ReLU anfangen. Wechsel zu Softplus nur, wenn du auf bestimmte Probleme stößt, die mit seinen Eigenschaften gelöst werden können.

Fazit

Kurz gesagt: Softplus bietet dir eine flüssige Alternative zu ReLU, wenn du sie brauchst.

Es wird ReLU nicht als Standard-Aktivierungsfunktion ersetzen – und das muss es auch nicht. Softplus löst bestimmte Probleme: sterbende Neuronen in flachen Netzwerken, Modelle, die nicht-negative Ergebnisse brauchen, und Aufgaben, bei denen ein gleichmäßiger Gradientenfluss für die Optimierung wichtig ist.

Man kriegt bessere mathematische Eigenschaften, muss dafür aber bei der Rechengeschwindigkeit Abstriche machen. Bei den meisten Deep-Learning-Projekten punkten ReLU wegen ihrer Einfachheit und Geschwindigkeit. Wenn du aber mit Wahrscheinlichkeitsmodellen, Bayes'schen Frameworks oder Regressionsaufgaben mit glatten Zielfunktionen arbeitest, ist Softplus die bessere Wahl.

Probier beides aus. Mach Experimente. Lass dich bei deiner Entscheidung von deinem speziellen Problem leiten.

Willst du mehr erfahren? Schau dir unsere tollen Ressourcen an:

• Deep Learning in Python
• Natürliche Sprachverarbeitung in Python
• Grundsätze der Softwareentwicklung in Python