programa
Imagina que observas una bandada de pájaros en vuelo. No hay ningún líder, nadie que les dé instrucciones, y sin embargo se lanzan en picado y planean juntos en perfecta armonía. Puede parecer un caos, pero hay un orden oculto. Puedes ver el mismo patrón en los bancos de peces que evitan a los depredadores o en las hormigas que encuentran el camino más corto hacia la comida. Estas criaturas se basan en reglas sencillas y en la comunicación local para abordar tareas sorprendentemente complejas sin un control central.
Esa es la magia de inteligencia de enjambre.
Podemos reproducir este comportamiento mediante algoritmos que resuelven problemas difíciles imitando la inteligencia de los enjambres.
¿Qué es la inteligencia de enjambre?
La inteligencia de enjambre es un enfoque computacional que resuelve problemas complejos imitando el comportamiento descentralizado y autoorganizado que se observa en los enjambres naturales, como las bandadas de pájaros o las colonias de hormigas.
Exploremos dos conceptos clave: descentralización y retroalimentación positiva.
Descentralización y emergencia
En el núcleo de la inteligencia de enjambre está el concepto de descentralización. En lugar de confiar en un líder central para dirigir las acciones, cada individuo, o "agente", opera de forma autónoma basándose en información local limitada.
Esta toma de decisiones descentralizada conduce a una propiedad emergente: un comportamiento complejo y organizado que surge de las simples interacciones de los agentes. En los sistemas de enjambre, el resultado global, o solución, no está preprogramado, sino que surge de forma natural de estas acciones individuales.
Tomemos como ejemplo las hormigas. Cuando busca comida, una hormiga explora aleatoriamente su entorno hasta que encuentra alimento, momento en el que deja un rastro de feromonas en su camino de vuelta a la colonia. Otras hormigas encuentran este rastro y es más probable que lo sigan, reforzando el camino si encuentran comida al final. Con el tiempo, las rutas más cortas o más eficientes atraen de forma natural a más hormigas, ya que a lo largo de estos caminos se acumulan rastros de feromonas más fuertes. Ninguna hormiga "conoce" la mejor ruta desde el principio, pero colectivamente, mediante decisiones descentralizadas y el refuerzo de las rutas exitosas, la colonia converge en la solución óptima.
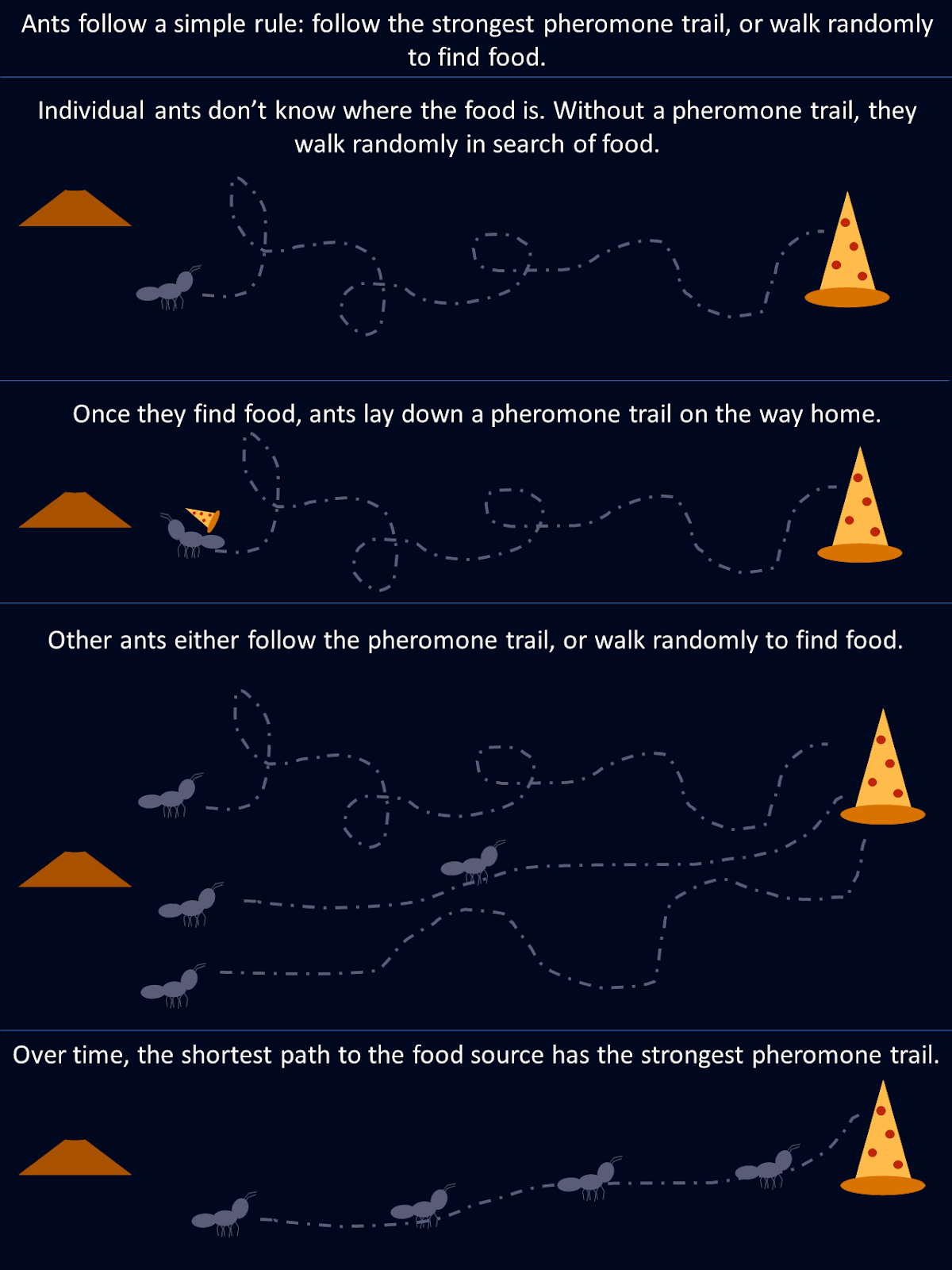
Este diagrama muestra cómo unas sencillas reglas seguidas por hormigas individuales dan como resultado una solución óptima para toda la colonia.
Retroalimentación positiva y adaptación
La retroalimentación positiva es un mecanismo de los sistemas de inteligencia de enjambre, donde las acciones exitosas son recompensadas y reforzadas. Esto conduce a un proceso de autoamplificación, como si las hormigas reforzaran los rastros de feromonas a lo largo de caminos de búsqueda más cortos. Este refuerzo de los comportamientos beneficiosos ayuda al enjambre a mejorar su rendimiento general a lo largo del tiempo.
En inteligencia artificiallos algoritmos de inteligencia de enjambre imitan esto ajustando los factores clave, como las probabilidades o los pesos, en función de la calidad de las soluciones encontradas. A medida que se descubren mejores soluciones, los agentes se centran cada vez más en ellas, lo que acelera el proceso de convergencia. Este bucle de retroalimentación dinámica permite a los sistemas de enjambre adaptarse a entornos cambiantes y perfeccionar su rendimiento.
Existen varios algoritmos de inteligencia de enjambre que imitan diferentes sistemas biológicos. Repasemos algunas de las más populares.
Optimización de colonias de hormigas (ACO)
La optimización de colonias de hormigas (ACO) es un algoritmo inspirado en el comportamiento de forrajeo de las hormigas descrito anteriormente. Está diseñado para resolver problemas de optimización especialmente aquellos en los que hay que encontrar la mejor solución posible entre muchas. Un ejemplo clásico es el problema del viajante de comercioen el que el objetivo es determinar la ruta más corta posible que conecte un conjunto de lugares.
Cómo funciona la optimización de colonias de hormigas
En la naturaleza, las hormigas se comunican dejando rastros de feromonas, que indican a otras hormigas el camino hacia una fuente de alimento. Cuantas más hormigas sigan ese rastro, más fuerte se hará. El ACO imita este comportamiento con feromonas representadas por valores matemáticos almacenados en una matriz de feromonas. Esta matriz lleva la cuenta de la deseabilidad de las distintas soluciones, y se actualiza a medida que avanza el algoritmo.
En el ACO, cada "hormiga artificial" representa una solución potencial al problema, como una ruta en el problema del viajante de comercio. El algoritmo comienza con todas las hormigas seleccionando caminos al azar, y los valores de feromona ayudan a guiar a las hormigas futuras. Estos valores se almacenan en una matriz en la que cada entrada corresponde al "nivel de feromona" entre dos puntos (como ciudades).
- Inicialización: El algoritmo empieza creando un conjunto aleatorio de soluciones, con hormigas que exploran diferentes caminos.
- Información feromónica y heurística: En la trayectoria de cada hormiga influyen dos factores principales: los niveles de feromona (lo "deseable" que es una solución según las iteraciones anteriores) y la información heurística (por ejemplo, la distancia entre dos ciudades). Los valores de feromona más altos hacen que un camino tenga más probabilidades de ser elegido.
- Actualización de las feromonas: Una vez que todas las hormigas han completado su camino, se actualizan los valores de feromona. Los caminos que formaban parte de soluciones mejores obtienen actualizaciones de feromonas más fuertes, mientras que los de soluciones subóptimas experimentan una evaporación. Matemáticamente, esto se hace aumentando los valores de feromona en la matriz para las buenas soluciones y reduciéndolos con el tiempo para las demás.
- Convergencia: A lo largo de iteraciones sucesivas, la matriz de feromonas evoluciona para reflejar las mejores soluciones, guiando a las hormigas hacia caminos más sólidos. A medida que se repite el proceso, las hormigas favorecen cada vez más estas rutas más exitosas, lo que conduce a la convergencia en la mejor solución.
Esta representación matemática de las feromonas permite al ACO equilibrar eficazmente la exploración y la explotación, buscando grandes espacios de soluciones sin atascarse en óptimos locales.
Optimización de colonias de hormigas Implementación en Python
Probemos un ejemplo, utilizando ACO para resolver un problema sencillo: encontrar el camino más corto entre puntos de un grafo.
Esta implementación de ACO simula cómo las "hormigas" artificiales recorren 20 nodos de un grafo para encontrar el camino más corto. Cada hormiga comienza en un nodo al azar y selecciona su siguiente movimiento basándose en los rastros de feromonas y las distancias entre nodos. Después de explorar todos los caminos, las hormigas vuelven a su punto de partida, completando un bucle completo.
Con el tiempo, las feromonas se actualizan: los caminos más cortos reciben un refuerzo más fuerte, mientras que otros se evaporan. Este proceso dinámico permite al algoritmo converger hacia una solución óptima.
import numpy as np
import matplotlib.pyplot as plt
# Graph class represents the environment where ants will travel
class Graph:
def __init__(self, distances):
# Initialize the graph with a distance matrix (distances between nodes)
self.distances = distances
self.num_nodes = len(distances) # Number of nodes (cities)
# Initialize pheromones for each path between nodes (same size as distances)
self.pheromones = np.ones_like(distances, dtype=float) # Start with equal pheromones
# Ant class represents an individual ant that travels across the graph
class Ant:
def __init__(self, graph):
self.graph = graph
# Choose a random starting node for the ant
self.current_node = np.random.randint(graph.num_nodes)
self.path = [self.current_node] # Start path with the initial node
self.total_distance = 0 # Start with zero distance traveled
# Unvisited nodes are all nodes except the starting one
self.unvisited_nodes = set(range(graph.num_nodes)) - {self.current_node}
# Select the next node for the ant to travel to, based on pheromones and distances
def select_next_node(self):
# Initialize an array to store the probability for each node
probabilities = np.zeros(self.graph.num_nodes)
# For each unvisited node, calculate the probability based on pheromones and distances
for node in self.unvisited_nodes:
if self.graph.distances[self.current_node][node] > 0: # Only consider reachable nodes
# The more pheromones and the shorter the distance, the more likely the node will be chosen
probabilities[node] = (self.graph.pheromones[self.current_node][node] ** 2 /
self.graph.distances[self.current_node][node])
probabilities /= probabilities.sum() # Normalize the probabilities to sum to 1
# Choose the next node based on the calculated probabilities
next_node = np.random.choice(range(self.graph.num_nodes), p=probabilities)
return next_node
# Move to the next node and update the ant's path
def move(self):
next_node = self.select_next_node() # Pick the next node
self.path.append(next_node) # Add it to the path
# Add the distance between the current node and the next node to the total distance
self.total_distance += self.graph.distances[self.current_node][next_node]
self.current_node = next_node # Update the current node to the next node
self.unvisited_nodes.remove(next_node) # Mark the next node as visited
# Complete the path by visiting all nodes and returning to the starting node
def complete_path(self):
while self.unvisited_nodes: # While there are still unvisited nodes
self.move() # Keep moving to the next node
# After visiting all nodes, return to the starting node to complete the cycle
self.total_distance += self.graph.distances[self.current_node][self.path[0]]
self.path.append(self.path[0]) # Add the starting node to the end of the path
# ACO (Ant Colony Optimization) class runs the algorithm to find the best path
class ACO:
def __init__(self, graph, num_ants, num_iterations, decay=0.5, alpha=1.0):
self.graph = graph
self.num_ants = num_ants # Number of ants in each iteration
self.num_iterations = num_iterations # Number of iterations
self.decay = decay # Rate at which pheromones evaporate
self.alpha = alpha # Strength of pheromone update
self.best_distance_history = [] # Store the best distance found in each iteration
# Main function to run the ACO algorithm
def run(self):
best_path = None
best_distance = np.inf # Start with a very large number for comparison
# Run the algorithm for the specified number of iterations
for _ in range(self.num_iterations):
ants = [Ant(self.graph) for _ in range(self.num_ants)] # Create a group of ants
for ant in ants:
ant.complete_path() # Let each ant complete its path
# If the current ant's path is shorter than the best one found so far, update the best path
if ant.total_distance < best_distance:
best_path = ant.path
best_distance = ant.total_distance
self.update_pheromones(ants) # Update pheromones based on the ants' paths
self.best_distance_history.append(best_distance) # Save the best distance for each iteration
return best_path, best_distance
# Update the pheromones on the paths after all ants have completed their trips
def update_pheromones(self, ants):
self.graph.pheromones *= self.decay # Reduce pheromones on all paths (evaporation)
# For each ant, increase pheromones on the paths they took, based on how good their path was
for ant in ants:
for i in range(len(ant.path) - 1):
from_node = ant.path[i]
to_node = ant.path[i + 1]
# Update the pheromones inversely proportional to the total distance traveled by the ant
self.graph.pheromones[from_node][to_node] += self.alpha / ant.total_distance
# Generate random distances between nodes (cities) for a 20-node graph
num_nodes = 20
distances = np.random.randint(1, 100, size=(num_nodes, num_nodes)) # Random distances between 1 and 100
np.fill_diagonal(distances, 0) # Distance from a node to itself is 0
graph = Graph(distances) # Create the graph with the random distances
aco = ACO(graph, num_ants=10, num_iterations=30) # Initialize ACO with 10 ants and 30 iterations
best_path, best_distance = aco.run() # Run the ACO algorithm to find the best path
# Print the best path found and the total distance
print(f"Best path: {best_path}")
print(f"Total distance: {best_distance}")
# Plotting the final solution (first plot) - Shows the final path found by the ants
def plot_final_solution(distances, path):
num_nodes = len(distances)
# Generate random coordinates for the nodes to visualize them on a 2D plane
coordinates = np.random.rand(num_nodes, 2) * 10
# Plot the nodes (cities) as red points
plt.scatter(coordinates[:, 0], coordinates[:, 1], color='red')
# Label each node with its index number
for i in range(num_nodes):
plt.text(coordinates[i, 0], coordinates[i, 1], f"{i}", fontsize=10)
# Plot the path (edges) connecting the nodes, showing the best path found
for i in range(len(path) - 1):
start, end = path[i], path[i + 1]
plt.plot([coordinates[start, 0], coordinates[end, 0]],
[coordinates[start, 1], coordinates[end, 1]],
'blue', linewidth=1.5)
plt.title("Final Solution: Best Path")
plt.show()
# Plotting the distance over iterations (second plot) - Shows how the path length improves over time
def plot_distance_over_iterations(best_distance_history):
# Plot the best distance found in each iteration (should decrease over time)
plt.plot(best_distance_history, color='green', linewidth=2)
plt.title("Trip Length Over Iterations")
plt.xlabel("Iteration")
plt.ylabel("Distance")
plt.show()
# Call the plotting functions to display the results
plot_final_solution(distances, best_path)
plot_distance_over_iterations(aco.best_distance_history)![Este gráfico muestra la solución final, la mejor ruta encontrada, para llegar a cada nodo en la distancia más corta. En esta ejecución, se encontró que la mejor ruta era [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], con una distancia total de 129.](https://media.datacamp.com/cms/google/ad_4nxcfk4zmpwq-et7v9dapocc9zbf7nm-mukhnmf83ih4ce-kh30kcuds_7ubqjmnv4ncv_iwr2nzg_oandfg1f6jc_wqkgdpu7jxlp4iilaruergyu4polxvvk5gu8x65jnuckjfj6knyoh-yqf8gpn_inper.png)
Este gráfico muestra la solución final, el mejor camino encontrado, para llegar a cada nodo en la distancia más corta. En esta ejecución, la mejor ruta resultó ser [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], con una distancia total de 129.
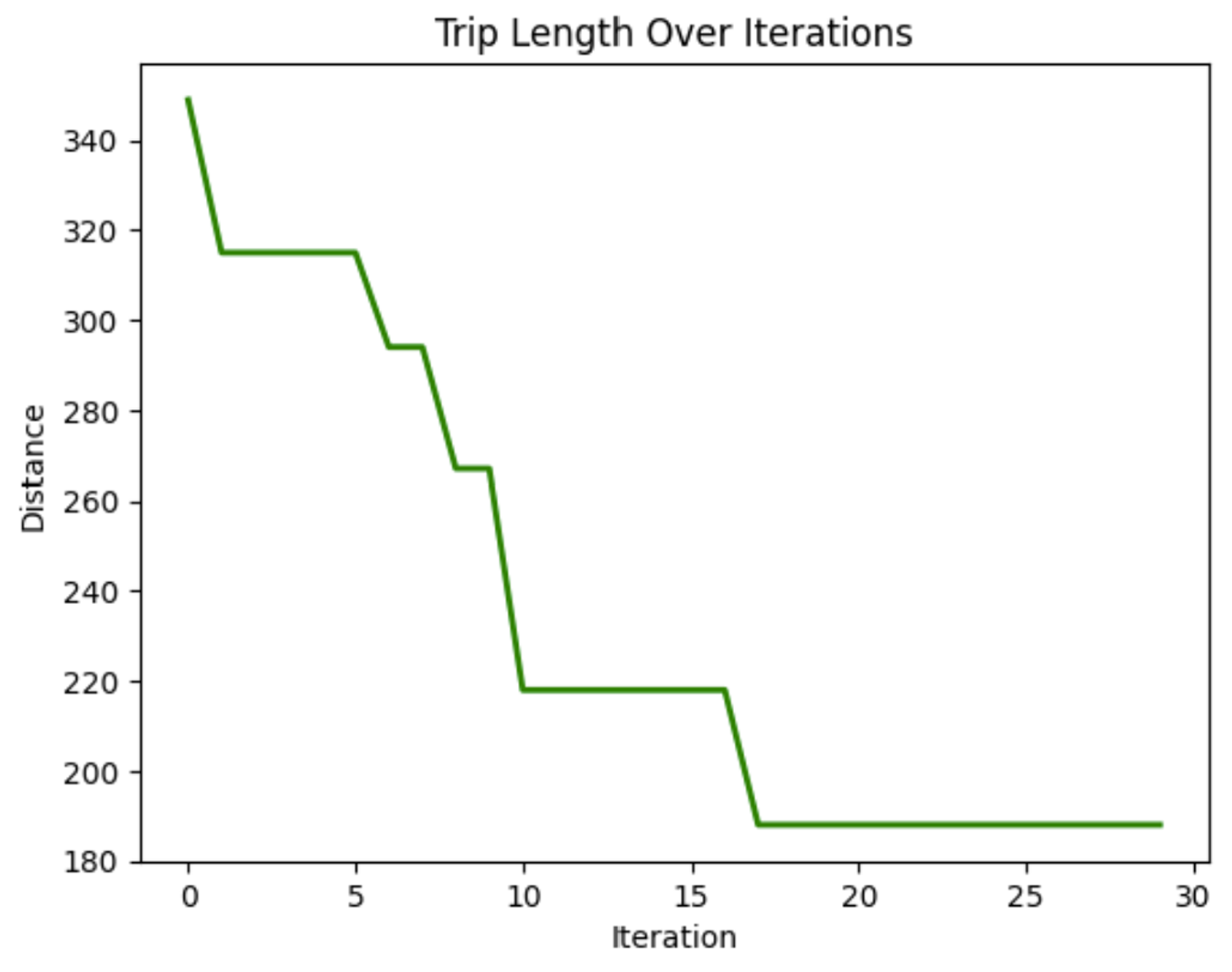
En este gráfico, podemos ver que la distancia recorrida al atravesar los nodos disminuye a lo largo de las iteraciones. Esto demuestra que el modelo va mejorando la duración del viaje con el tiempo.
Aplicaciones de la optimización de colonias de hormigas
La adaptabilidad y eficacia de la ACO la convierten en una poderosa herramienta en diversos sectores. Algunas aplicaciones son:
- Problemas de encaminamiento: El ACO se utiliza para optimizar el encaminamiento de redes (por ejemplo, determinar el camino más corto para los paquetes de datos en una red), el transporte y los servicios de entrega.
- Programación: El ACO puede aplicarse a la programación de tareas en la fabricación o la logística, garantizando que los recursos se asignen de forma eficiente.
- Asignación de recursos: El algoritmo puede utilizarse para asignar recursos limitados, como en la gestión de proyectos o en operaciones complejas en las que deben tenerse en cuenta múltiples variables.
La fuerza del ACO reside en su capacidad de evolucionar y adaptarse, lo que lo hace adecuado para entornos dinámicos en los que las condiciones pueden cambiar, como el encaminamiento del tráfico en tiempo real o la planificación industrial.
Desarrollar aplicaciones de IA
Optimización por enjambre de partículas (PSO)
La optimización por enjambre de partículas (PSO) se inspira en el comportamiento de las bandadas de pájaros y los bancos de peces. En estos sistemas naturales, los individuos se mueven basándose en sus propias experiencias previas y en las posiciones de sus vecinos, ajustándose gradualmente para seguir a los miembros más exitosos del grupo. La PSO aplica este concepto a los problemas de optimización, en los que las partículas, llamadas agentes, se mueven por el espacio de búsqueda para encontrar una solución óptima.
En comparación con el ACO, el PSO opera en espacios continuos en lugar de discretos. En el ACO, la atención se centra en la búsqueda de trayectorias y en las elecciones discretas, mientras que el PSO es más adecuado para los problemas que implican variables continuas, como el ajuste de parámetros.
En la PSO, las partículas exploran un espacio de búsqueda. Ajustan sus posiciones en función de dos factores principales: su posición personal mejor conocida y la posición mejor conocida de todo el enjambre. Este doble mecanismo de retroalimentación les permite converger hacia el óptimo global.
Cómo funciona la optimización por enjambre de partículas
El proceso comienza con un enjambre de partículas inicializadas aleatoriamente en el espacio solución. Cada partícula representa una posible solución al problema de optimización. A medida que las partículas se mueven, recuerdan sus mejores posiciones personales (la mejor solución que han encontrado hasta el momento) y son atraídas hacia la mejor posición global (la mejor solución que ha encontrado cualquier partícula).
Este movimiento está impulsado por dos factores: la explotación y la exploración. La explotación implica refinar la búsqueda en torno a la mejor solución actual, mientras que la exploración anima a las partículas a buscar en otras partes del espacio de soluciones para evitar quedarse atascadas en óptimos locales. Al equilibrar estas dos dinámicas, la PSO converge eficazmente en la mejor solución.
Optimización por enjambre de partículas Implementación en Python
En gestión de carteras financierasencontrar la mejor forma de asignar los activos para obtener el máximo rendimiento manteniendo los riesgos bajos puede ser complicado. Utilicemos una PSO para averiguar qué combinación de activos nos dará el mayor rendimiento de la inversión.
El código siguiente muestra cómo funciona PSO para optimizar una cartera financiera ficticia. Empieza con asignaciones de activos aleatorias, y luego las ajusta a lo largo de varias iteraciones basándose en lo que funciona mejor, encontrando gradualmente la combinación óptima de activos para obtener el mayor rendimiento con el menor riesgo.
import numpy as np
import matplotlib.pyplot as plt
# Define the PSO parameters
class Particle:
def __init__(self, n_assets):
# Initialize a particle with random weights and velocities
self.position = np.random.rand(n_assets)
self.position /= np.sum(self.position) # Normalize weights so they sum to 1
self.velocity = np.random.rand(n_assets)
self.best_position = np.copy(self.position)
self.best_score = float('inf') # Start with a very high score
def objective_function(weights, returns, covariance):
"""
Calculate the portfolio's performance.
- weights: Asset weights in the portfolio.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
portfolio_return = np.dot(weights, returns) # Calculate the portfolio return
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(covariance, weights))) # Calculate portfolio risk (standard deviation)
return -portfolio_return / portfolio_risk # We want to maximize return and minimize risk
def update_particles(particles, global_best_position, returns, covariance, w, c1, c2):
"""
Update the position and velocity of each particle.
- particles: List of particle objects.
- global_best_position: Best position found by all particles.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
- w: Inertia weight to control particle's previous velocity effect.
- c1: Cognitive coefficient to pull particles towards their own best position.
- c2: Social coefficient to pull particles towards the global best position.
"""
for particle in particles:
# Random coefficients for velocity update
r1, r2 = np.random.rand(len(particle.position)), np.random.rand(len(particle.position))
# Update velocity
particle.velocity = (w * particle.velocity +
c1 * r1 * (particle.best_position - particle.position) +
c2 * r2 * (global_best_position - particle.position))
# Update position
particle.position += particle.velocity
particle.position = np.clip(particle.position, 0, 1) # Ensure weights are between 0 and 1
particle.position /= np.sum(particle.position) # Normalize weights to sum to 1
# Evaluate the new position
score = objective_function(particle.position, returns, covariance)
if score < particle.best_score:
# Update the particle's best known position and score
particle.best_position = np.copy(particle.position)
particle.best_score = score
def pso_portfolio_optimization(n_particles, n_iterations, returns, covariance):
"""
Perform Particle Swarm Optimization to find the optimal asset weights.
- n_particles: Number of particles in the swarm.
- n_iterations: Number of iterations for the optimization.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
# Initialize particles
particles = [Particle(len(returns)) for _ in range(n_particles)]
# Initialize global best position
global_best_position = np.random.rand(len(returns))
global_best_position /= np.sum(global_best_position)
global_best_score = float('inf')
# PSO parameters
w = 0.5 # Inertia weight: how much particles are influenced by their own direction
c1 = 1.5 # Cognitive coefficient: how well particles learn from their own best solutions
c2 = 0.5 # Social coefficient: how well particles learn from global best solutions
history = [] # To store the best score at each iteration
for _ in range(n_iterations):
update_particles(particles, global_best_position, returns, covariance, w, c1, c2)
for particle in particles:
score = objective_function(particle.position, returns, covariance)
if score < global_best_score:
# Update the global best position and score
global_best_position = np.copy(particle.position)
global_best_score = score
# Store the best score (negative return/risk ratio) for plotting
history.append(-global_best_score)
return global_best_position, history
# Example data for 3 assets
returns = np.array([0.02, 0.28, 0.15]) # Expected returns for each asset
covariance = np.array([[0.1, 0.02, 0.03], # Covariance matrix for asset risks
[0.02, 0.08, 0.04],
[0.03, 0.04, 0.07]])
# Run the PSO algorithm
n_particles = 10 # Number of particles
n_iterations = 10 # Number of iterations
best_weights, optimization_history = pso_portfolio_optimization(n_particles, n_iterations, returns, covariance)
# Plotting the optimization process
plt.figure(figsize=(12, 6))
plt.plot(optimization_history, marker='o')
plt.title('Portfolio Optimization Using PSO')
plt.xlabel('Iteration')
plt.ylabel('Objective Function Value (Negative of Return/Risk Ratio)')
plt.grid(False) # Turn off gridlines
plt.show()
# Display the optimal asset weights
print(f"Optimal Asset Weights: {best_weights}")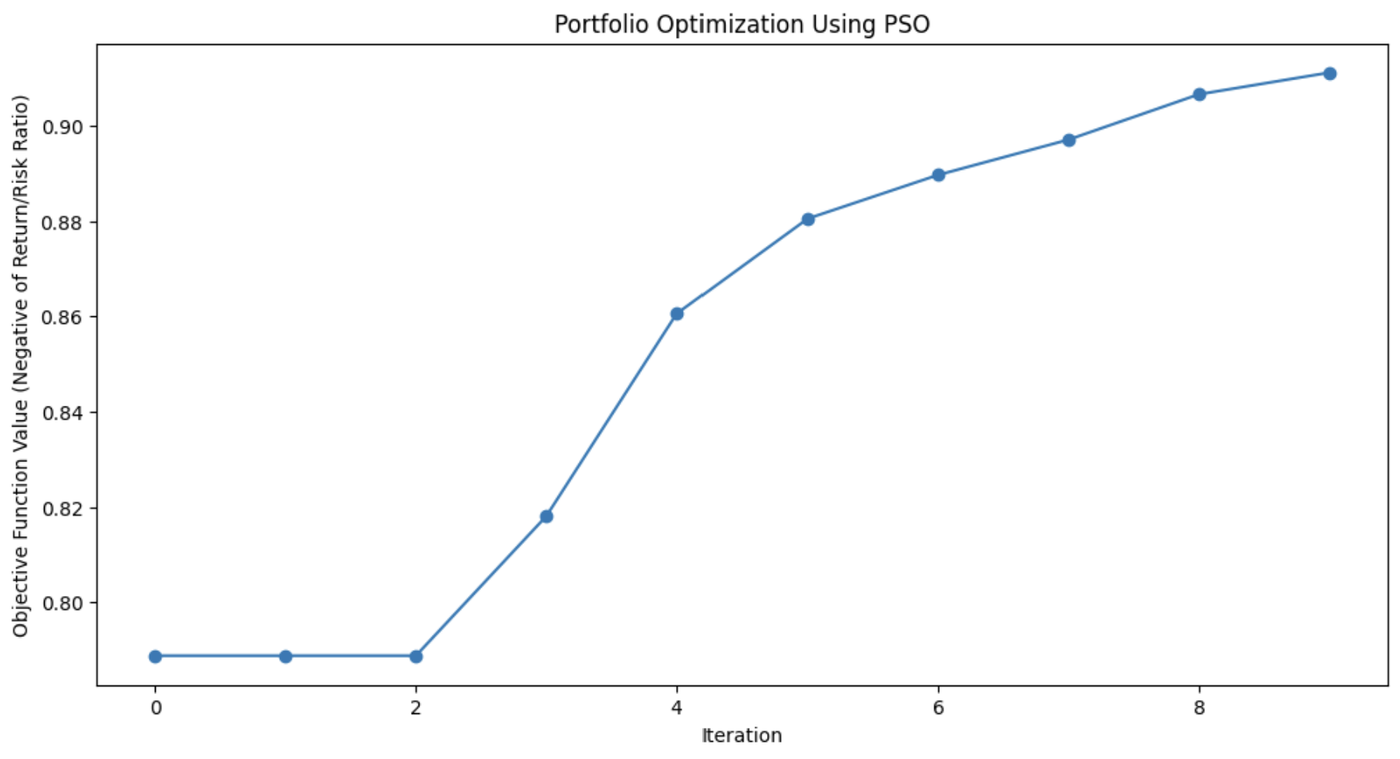
Este gráfico demuestra cuánto mejoró el algoritmo PSO la combinación de activos de la cartera con cada iteración.
Aplicaciones de la optimización por enjambre de partículas
La PSO se utiliza por su sencillez y eficacia para resolver diversos problemas de optimización, sobre todo en dominios continuos. Su flexibilidad lo hace útil para muchas situaciones del mundo real en las que se necesitan soluciones precisas.
Estas aplicaciones incluyen:
- Aprendizaje automático: PSO puede aplicarse para ajustar hiperparámetros en algoritmos de aprendizaje automáticoayudando a encontrar las mejores configuraciones del modelo.
- Diseño de ingeniería: PSO es útil para optimizar parámetros de diseño de sistemas como componentes aeroespaciales o circuitos eléctricos.
- Modelización financiera: En finanzas, PSO puede ayudar en la optimización de carteras, minimizando el riesgo y maximizando el rendimiento.
La capacidad de PSO para explorar eficazmente los espacios de soluciones hace que sea aplicable en todos los campos, desde la robótica a la gestión de la energía o la logística.
Colonia artificial de abejas (ABC)
El algoritmo de la colonia artificial de abejas (ABC) se basa en el comportamiento de búsqueda de alimento de las abejas.
En la naturaleza, las abejas buscan eficazmente las fuentes de néctar y comparten esta información con otros miembros de la colmena. ABC captura este proceso de búsqueda colaborativa y lo aplica a problemas de optimización, especialmente a los que implican espacios complejos y de alta dimensión.
Lo que diferencia al ABC de otros algoritmos de inteligencia de enjambre es su capacidad para equilibrar la explotación, centrándose en refinar las soluciones actuales, y la exploración, buscando soluciones nuevas y potencialmente mejores. Esto hace que el ABC sea especialmente útil para problemas a gran escala en los que la optimización global es clave.
Cómo funciona una colonia artificial de abejas
En el algoritmo ABC, el enjambre de abejas se divide en tres roles especializados: abejas empleadas, vigilantes y exploradoras. Cada una de estas funciones imita un aspecto diferente de cómo las abejas buscan y explotan las fuentes de alimento en la naturaleza.
- Abejas empleadas: Estas abejas se encargan de explorar las fuentes de alimento conocidas, que representan las soluciones actuales en el problema de optimización. Evalúan la calidad (aptitud) de estas fuentes y comparten la información con el resto de la colmena.
- Abejas observadoras: Tras recabar información de las abejas empleadas, los observadores seleccionan qué fuentes de alimento explorar más a fondo. Basan sus elecciones en la calidad de las soluciones compartidas por las abejas empleadas, centrándose más en las mejores opciones, refinando así la búsqueda de una solución óptima.
- Abejas exploradoras: Cuando la fuente de alimento (solución) de una abeja empleada se agota o se estanca (cuando no se encuentra ninguna mejora tras un determinado número de iteraciones), la abeja se convierte en exploradora. Los exploradores exploran nuevas zonas del espacio de soluciones, buscando fuentes de alimento potencialmente inexploradas, inyectando así diversidad al proceso de búsqueda.
Esta dinámica permite a ABC equilibrar la búsqueda entre la exploración intensiva de áreas prometedoras y la exploración amplia de nuevas áreas del espacio de búsqueda. Esto ayuda al algoritmo a evitar quedar atrapado en óptimos locales y aumenta sus posibilidades de encontrar un óptimo global.
Implementación en Python de la colonia artificial de abejas
El sitio función Rastrigin es un problema popular en optimización, conocido por sus numerosos mínimos locales, lo que lo convierte en un duro reto para muchos algoritmos. El objetivo es sencillo: encontrar el mínimo global.
En este ejemplo, utilizaremos el algoritmo de la colonia artificial de abejas para abordar este problema. Cada abeja del algoritmo ABC explora el espacio de búsqueda, buscando mejores soluciones para minimizar la función. El código simula abejas que exploran, explotan y exploran nuevas zonas, garantizando un equilibrio entre exploración y explotación.
import numpy as np
import matplotlib.pyplot as plt
# Rastrigin function: The objective is to minimize this function
def rastrigin(X):
A = 10
return A * len(X) + sum([(x ** 2 - A * np.cos(2 * np.pi * x)) for x in X])
# Artificial Bee Colony (ABC) algorithm for continuous optimization of Rastrigin function
def artificial_bee_colony_rastrigin(n_iter=100, n_bees=30, dim=2, bound=(-5.12, 5.12)):
"""
Apply Artificial Bee Colony (ABC) algorithm to minimize the Rastrigin function.
Parameters:
n_iter (int): Number of iterations
n_bees (int): Number of bees in the population
dim (int): Number of dimensions (variables)
bound (tuple): Bounds for the search space (min, max)
Returns:
tuple: Best solution found, best fitness value, and list of best fitness values per iteration
"""
# Initialize the bee population with random solutions within the given bounds
bees = np.random.uniform(bound[0], bound[1], (n_bees, dim))
best_bee = bees[0]
best_fitness = rastrigin(best_bee)
best_fitnesses = []
for iteration in range(n_iter):
# Employed bees phase: Explore new solutions based on the current bees
for i in range(n_bees):
# Generate a new candidate solution by perturbing the current bee's position
new_bee = bees[i] + np.random.uniform(-1, 1, dim)
new_bee = np.clip(new_bee, bound[0], bound[1]) # Keep within bounds
# Evaluate the fitness of the new solution
new_fitness = rastrigin(new_bee)
if new_fitness < rastrigin(bees[i]):
bees[i] = new_bee # Update bee if the new solution is better
# Onlooker bees phase: Exploit good solutions
fitnesses = np.array([rastrigin(bee) for bee in bees])
probabilities = 1 / (1 + fitnesses) # Higher fitness gets higher chance
probabilities /= probabilities.sum() # Normalize probabilities
for i in range(n_bees):
if np.random.rand() < probabilities[i]:
selected_bee = bees[i]
# Generate a new candidate solution by perturbing the selected bee
new_bee = selected_bee + np.random.uniform(-0.5, 0.5, dim)
new_bee = np.clip(new_bee, bound[0], bound[1])
if rastrigin(new_bee) < rastrigin(selected_bee):
bees[i] = new_bee
# Scouting phase: Randomly reinitialize some bees to explore new areas
if np.random.rand() < 0.1: # 10% chance to reinitialize a bee
scout_index = np.random.randint(n_bees)
bees[scout_index] = np.random.uniform(bound[0], bound[1], dim)
# Track the best solution found so far
current_best_bee = bees[np.argmin(fitnesses)]
current_best_fitness = min(fitnesses)
if current_best_fitness < best_fitness:
best_fitness = current_best_fitness
best_bee = current_best_bee
best_fitnesses.append(best_fitness)
return best_bee, best_fitness, best_fitnesses
# Apply ABC to minimize the Rastrigin function
best_solution, best_fitness, best_fitnesses = artificial_bee_colony_rastrigin()
# Display results
print("Best Solution (x, y):", best_solution)
print("Best Fitness (Minimum Value):", best_fitness)
# Plot the performance over iterations
plt.figure()
plt.plot(best_fitnesses)
plt.title('Performance of ABC on Rastrigin Function Optimization')
plt.xlabel('Iterations')
plt.ylabel('Best Fitness (Lower is Better)')
plt.grid(True)
plt.show()
# Plot a surface graph of the Rastrigin function
x = np.linspace(-5.12, 5.12, 200)
y = np.linspace(-5.12, 5.12, 200)
X, Y = np.meshgrid(x, y)
Z = 10 * 2 + (X ** 2 - 10 * np.cos(2 * np.pi * X)) + (Y ** 2 - 10 * np.cos(2 * np.pi * Y))
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.colorbar(label='Function Value')
plt.scatter(best_solution[0], best_solution[1], c='red', label='Best Solution')
plt.title('Rastrigin Function Optimization with ABC')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()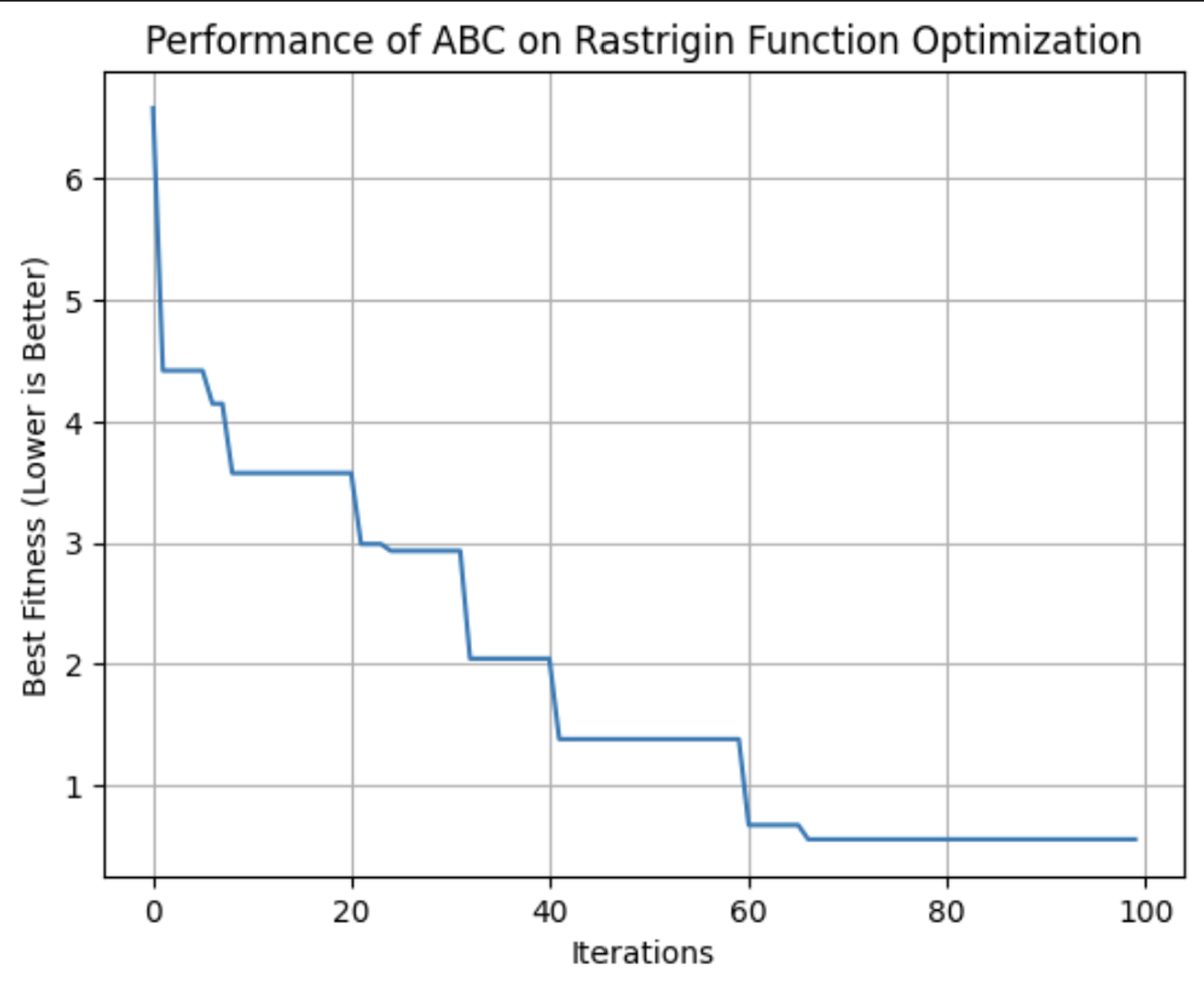
Este gráfico muestra la aptitud de la mejor solución encontrada por el algoritmo ABC con cada iteración. En esta ejecución, alcanzó su idoneidad óptima alrededor de la iteración 64.
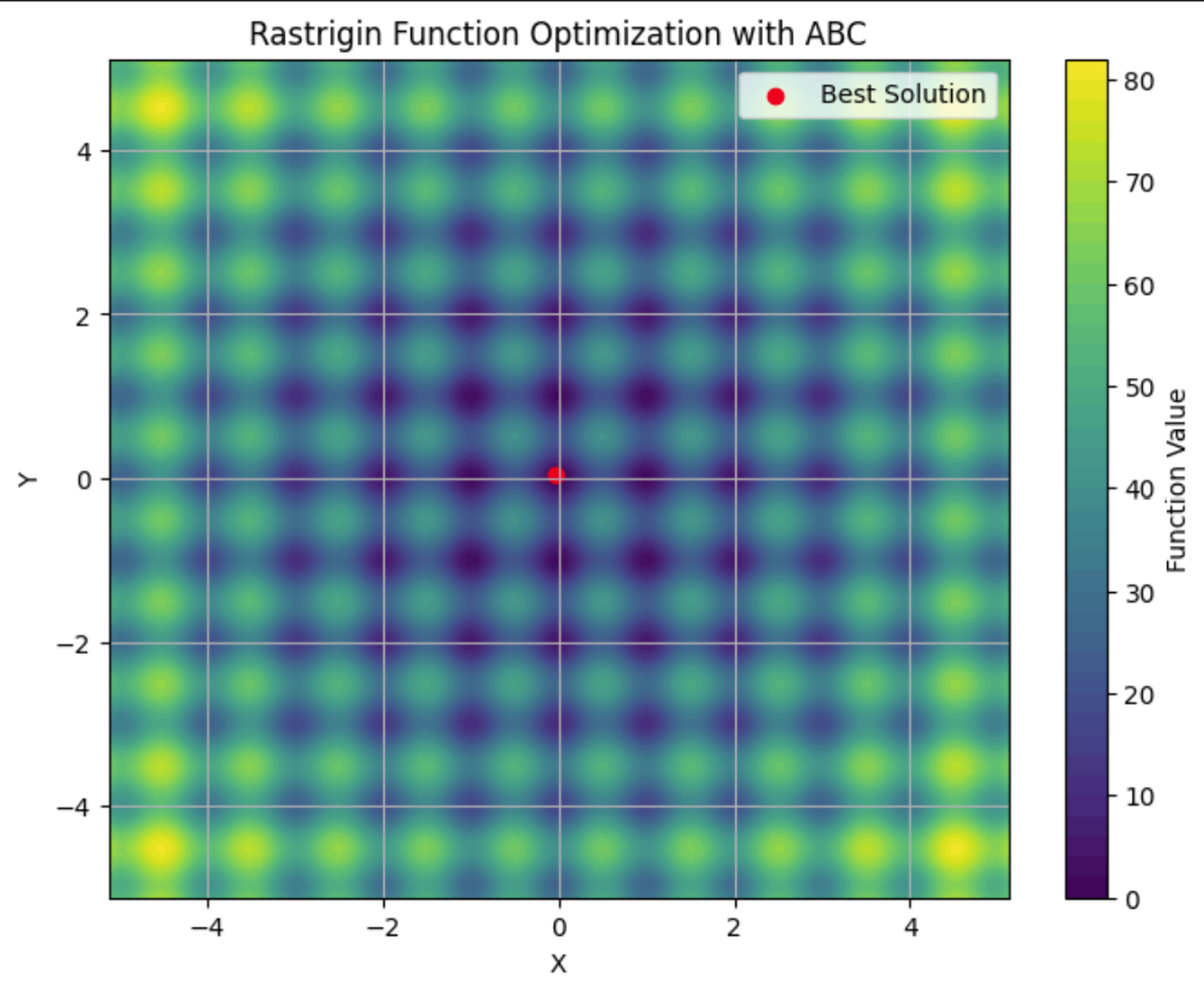
Aquí puedes ver la función Rastrigin trazada en un gráfico de contorno, con sus numerosos mínimos locales. El punto rojo es el mínimo global encontrado por el algoritmo ABC que ejecutamos.
Aplicaciones de las colonias artificiales de abejas
El algoritmo ABC es una herramienta robusta para resolver problemas de optimización. Su capacidad para explorar eficazmente espacios de búsqueda amplios y complejos lo convierte en la opción preferida de los sectores en los que la adaptabilidad y la escalabilidad son fundamentales.
Estas aplicaciones incluyen:
- Telecomunicaciones: El ABC puede utilizarse para optimizar la ubicación de los recursos de red y las antenas, maximizando la cobertura y la intensidad de la señal y minimizando los costes.
- Ingeniería: ABC puede afinar los parámetros en la optimización del diseño estructural.
- Ciencia de datos: El ABC puede aplicarse a la selección de características, para identificar las variables más importantes de un conjunto de datos para el aprendizaje automático.
ABC es un algoritmo flexible adecuado para cualquier problema en el que haya que encontrar soluciones óptimas en entornos dinámicos y de alta dimensión. Su naturaleza descentralizada lo hace adecuado para situaciones en las que otros algoritmos pueden tener dificultades para equilibrar la exploración y la explotación de forma eficaz.
Comparación de algoritmos de inteligencia de enjambre
Existen múltiples algoritmos de inteligencia de enjambre, cada uno con atributos diferentes. Al decidir cuál utilizar, es importante sopesar sus puntos fuertes y débiles para decidir cuál se adapta mejor a tus necesidades.
El ACO es eficaz para problemas combinatorios como el encaminamiento y la programación, pero puede necesitar importantes recursos informáticos. La PSO es más sencilla y destaca en la optimización continua, como el ajuste de hiperparámetros, pero puede tener problemas con los óptimos locales. El ABC equilibra con éxito la exploración y la explotación, aunque requiere un ajuste cuidadoso.
Otros algoritmos de inteligencia de enjambre, como Algoritmo Firefly y Optimización por búsqueda de cucotambién ofrecen ventajas únicas para determinados tipos de problemas de optimización .
|
Algoritmo |
Puntos fuertes |
Puntos débiles |
Bibliotecas preferidas |
Las mejores aplicaciones |
|
Optimización de colonias de hormigas (ACO) |
Eficaz para problemas combinatorios y maneja bien los espacios discretos complejos |
Intensivo desde el punto de vista informático y requiere un ajuste fino |
Problemas de rutas, programación y asignación de recursos |
|
|
Optimización por enjambre de partículas (PSO) |
Bueno para la optimización continua y sencillo y fácil de aplicar |
Puede converger a óptimos locales y es menos eficaz para problemas discretos |
Ajuste de hiperparámetros, diseño de ingeniería, modelización financiera |
|
|
Colonia artificial de abejas (ABC) |
Adaptable a problemas grandes y dinámicos y a una exploración y explotación equilibradas |
Intensivo desde el punto de vista informático y requiere un ajuste cuidadoso de los parámetros |
Telecomunicaciones, optimización a gran escala y espacios de alta dimensión |
|
|
Algoritmo Firefly (FA) |
Destaca en la optimización multimodal y tiene una gran capacidad de búsqueda global |
Sensible a los ajustes de los parámetros y convergencia más lenta |
Procesamiento de imágenes, diseño de ingeniería y optimización multimodal |
|
|
Búsqueda Cuco (CS) |
Eficaz para resolver problemas de optimización y con gran capacidad de exploración |
Puede converger prematuramente y el rendimiento depende de la sintonización |
Programación, selección de características y aplicaciones de ingeniería |
Retos y limitaciones
Los algoritmos de inteligencia de enjambre, como muchas técnicas de aprendizaje automático, se enfrentan a retos que pueden afectar a su rendimiento. Entre ellas están:
- Convergencia prematura: El enjambre puede asentarse en una solución subóptima demasiado rápido.
- Ajuste de parámetros: Conseguir resultados óptimos suele requerir un ajuste cuidadoso de la configuración del algoritmo.
- Recursos informáticos y escalabilidad: Estos algoritmos pueden ser intensivos desde el punto de vista computacional, especialmente con problemas más grandes y complejos, y su rendimiento podría degradarse a medida que la complejidad del problema complejidad del problema del problema.
- Naturaleza estocástica: La aleatoriedad inherente a estos algoritmos puede provocar variabilidad en los resultados.
Últimas investigaciones y avances
Una tendencia notable es la integración de la inteligencia de enjambre con otras técnicas de aprendizaje automático. Los investigadores están explorando cómo los algoritmos de enjambre pueden mejorar tareas como la selección de características y optimización de hiperparámetros. Consulta Un algoritmo híbrido de optimización por enjambre de partículas para resolver problemas de ingeniería.
Los avances recientes también se centran en abordar algunos de los retos tradicionales asociados a la inteligencia de enjambre, como la convergencia prematura. Se están desarrollando nuevos algoritmos y técnicas para mitigar el riesgo de converger en soluciones subóptimas. Para más información, consulta Enfoques basados en la memoria para eliminar la convergencia prematura en la optimización por enjambre de partículas
La escalabilidad es otra importante área de investigación. A medida que los problemas se hacen cada vez más complejos y los volúmenes de datos crecen, los investigadores están trabajando en formas de hacer que los algoritmos de inteligencia de enjambre sean más escalables y eficientes. Esto incluye el desarrollo de algoritmos que puedan manejar grandes conjuntos de datos y espacios de alta dimensión con mayor eficacia, al tiempo que se optimizan los recursos informáticos para reducir el tiempo y el coste asociados a la ejecución de estos algoritmos. Para más información, consulta Avances recientes en la teoría y aplicabilidad de la búsqueda en enjambre.
Los algoritmos de enjambre se están aplicando a problemas de robóticaa grandes modelos lingüísticos (LLM), al diagnóstico médico. Existen investigaciones en curso sobre si estos algoritmos pueden ser útiles para ayudar a los LLM a olvidar estratégicamente la información para cumplir la normativa sobreel Derecho al Olvido. Y, por supuesto, los algoritmos de enjambre tienen multitud de aplicaciones en la ciencia de datos.
Conclusión
La inteligencia de enjambre ofrece potentes soluciones para los problemas de optimización en diversos sectores. Sus principios de descentralización, retroalimentación positiva y adaptación le permiten abordar tareas complejas y dinámicas con las que los algoritmos tradicionales podrían tener dificultades.
Consulta esta revisión del estado actual de los algoritmos de enjambre, "Swarm intelligence: Un estudio de clasificación de modelos y aplicaciones".
Para profundizar en las aplicaciones empresariales de la IA, consulta Estrategia de Inteligencia Artificial (IA) o Inteligencia Artificial para líderes empresariales. Para conocer otros algoritmos que imitan a la naturaleza, consulta Algoritmo genético: Guía completa con implementación en Python.

Soy doctor con 13 años de experiencia trabajando con datos en un entorno de investigación biológica. Creo software en varios lenguajes de programación, como Python, MATLAB y R. Me apasiona compartir mi amor por el aprendizaje con el mundo.