Programa
Imagine observar um bando de pássaros voando. Não há um líder, ninguém dando instruções, mas eles voam e deslizam juntos em perfeita harmonia. Pode parecer um caos, mas há uma ordem oculta. Você pode ver o mesmo padrão em cardumes de peixes que evitam predadores ou em formigas que encontram o caminho mais curto para o alimento. Essas criaturas contam com regras simples e comunicação local para realizar tarefas surpreendentemente complexas sem controle central.
Essa é a magia da inteligência de enxame.
Podemos replicar esse comportamento usando algoritmos que resolvem problemas difíceis imitando a inteligência de enxame.
O que é Swarm Intelligence?
A inteligência de enxame é uma abordagem computacional que resolve problemas complexos imitando o comportamento descentralizado e auto-organizado observado em enxames naturais, como bandos de pássaros ou colônias de formigas.
Vamos explorar dois conceitos-chave: descentralização e feedback positivo.
Descentralização e surgimento
No centro da inteligência de enxame está o conceito de descentralização. Em vez de depender de um líder central para direcionar as ações, cada indivíduo, ou "agente", opera de forma autônoma com base em informações locais limitadas.
Essa tomada de decisão descentralizada leva a uma propriedade emergente - um comportamento complexo e organizado que surge das interações simples dos agentes. Nos sistemas de enxame, o resultado geral, ou solução, não é pré-programado, mas emerge naturalmente dessas ações individuais.
Tomemos como exemplo as formigas. Ao procurar alimentos, a formiga explora aleatoriamente o ambiente até encontrar comida e, nesse momento, deixa uma trilha de feromônio no caminho de volta para a colônia. Outras formigas encontram essa trilha e são mais propensas a segui-la, reforçando o caminho se encontrarem alimento no final. Com o passar do tempo, rotas mais curtas ou mais eficientes atraem naturalmente mais formigas à medida que trilhas de feromônio mais fortes se acumulam ao longo desses caminhos. Nenhuma formiga "conhece" a melhor rota desde o início, mas coletivamente, por meio de decisões descentralizadas e do reforço de caminhos bem-sucedidos, a colônia converge para a solução ideal.
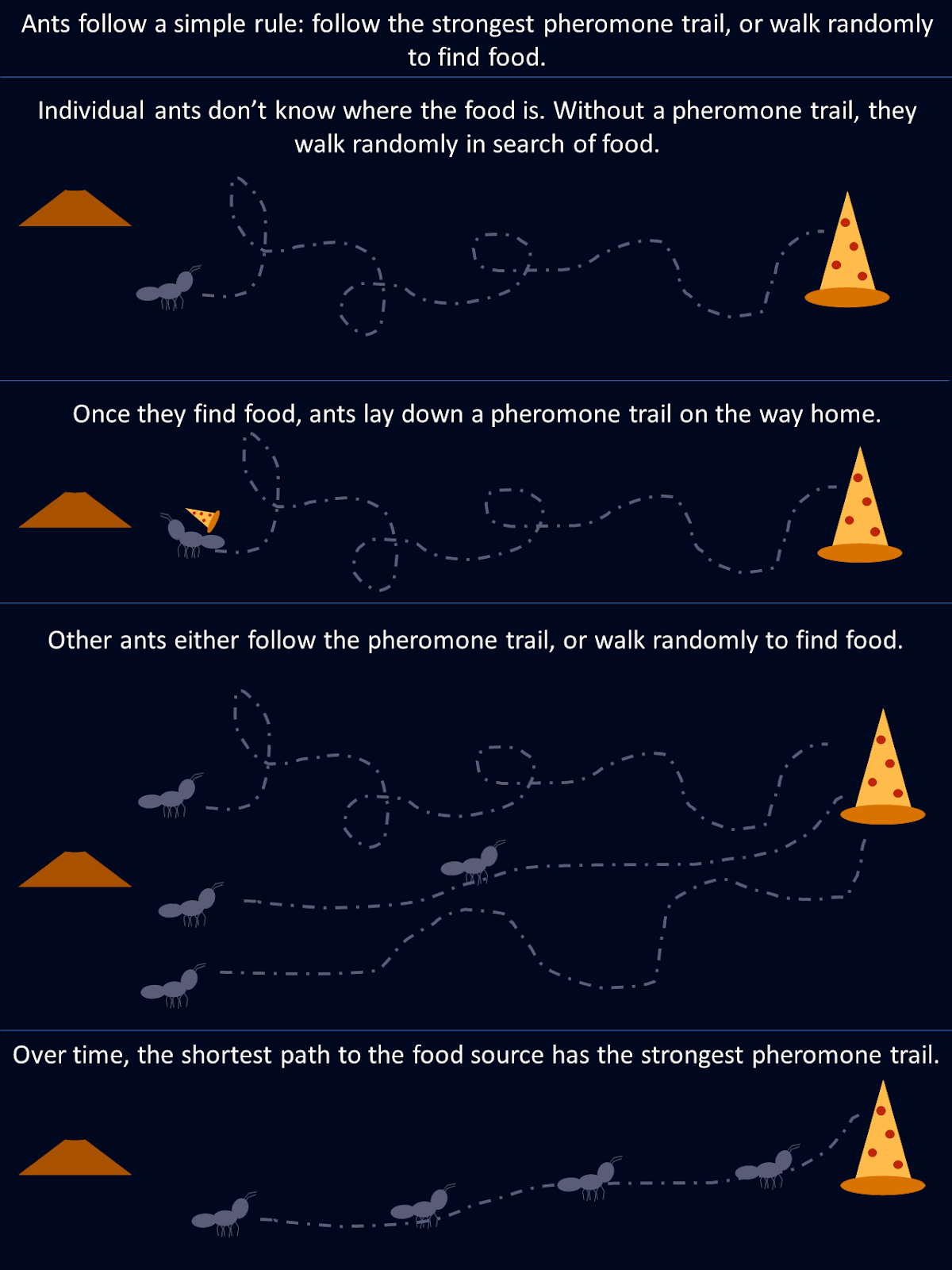
Esse diagrama mostra como regras simples seguidas por formigas individuais resultam em uma solução ideal para toda a colônia.
Feedback positivo e adaptação
O feedback positivo é um mecanismo nos sistemas de inteligência de enxame, em que as ações bem-sucedidas são recompensadas e reforçadas. Isso leva a um processo de autoamplificação, como se as formigas fortalecessem as trilhas de feromônio ao longo de caminhos de forrageamento mais curtos. Esse reforço de comportamentos benéficos ajuda o enxame a melhorar seu desempenho geral ao longo do tempo.
Em inteligência artificialos algoritmos de inteligência de enxame imitam isso, ajustando os principais fatores, como probabilidades ou pesos, com base na qualidade das soluções encontradas. À medida que soluções melhores são descobertas, os agentes se concentram cada vez mais nelas, o que acelera o processo de convergência. Esse ciclo de feedback dinâmico permite que os sistemas de enxame se adaptem a ambientes em constante mudança e aprimorem seu desempenho.
Há vários algoritmos de inteligência de enxame que imitam diferentes sistemas biológicos. Vamos examinar alguns dos mais populares.
Otimização por colônia de formigas (ACO)
A otimização de colônia de formigas (ACO) é um algoritmo inspirado no comportamento de forrageamento das formigas descrito acima. Ele foi projetado para resolver problemas de otimização combinatória particularmente aqueles em que precisamos encontrar a melhor solução possível entre muitas. Um exemplo clássico disso é o problema do problema do caixeiro viajanteem que o objetivo é determinar a rota mais curta possível que conecta um conjunto de locais.
Como funciona a otimização de colônias de formigas
Na natureza, as formigas se comunicam deixando rastros de feromônio, que sinalizam para outras formigas o caminho para uma fonte de alimento. Quanto mais formigas seguirem essa trilha, mais forte ela se tornará. O ACO imita esse comportamento com feromônios representados por valores matemáticos armazenados em uma matriz de feromônios. Essa matriz mantém o controle da conveniência de diferentes soluções e é atualizada à medida que o algoritmo avança.
No ACO, cada "formiga artificial" representa uma possível solução para o problema, como uma rota no problema do caixeiro viajante. O algoritmo começa com todas as formigas selecionando caminhos aleatoriamente, e os valores de feromônio ajudam a orientar as futuras formigas. Esses valores são armazenados em uma matriz em que cada entrada corresponde ao "nível de feromônio" entre dois pontos (como cidades).
- Inicialização: O algoritmo começa criando um conjunto aleatório de soluções, com as formigas explorando diferentes caminhos.
- Informações de feromônio e heurísticas: O caminho de cada formiga é influenciado por dois fatores principais: níveis de feromônio (quão "desejável" é uma solução com base em iterações anteriores) e informações heurísticas (por exemplo, a distância entre duas cidades). Valores mais altos de feromônio aumentam a probabilidade de um caminho ser escolhido.
- Atualização de feromônios: Depois que todas as formigas concluírem seus caminhos, os valores de feromônio são atualizados. Os caminhos que faziam parte das melhores soluções recebem atualizações de feromônio mais fortes, enquanto os caminhos em soluções abaixo do ideal sofrem evaporação. Matematicamente, isso é feito aumentando os valores de feromônio na matriz para boas soluções e reduzindo-os ao longo do tempo para outras soluções.
- Convergência: Em iterações sucessivas, a matriz de feromônio evolui para refletir as melhores soluções, orientando as formigas para caminhos mais fortes. À medida que o processo se repete, as formigas favorecem cada vez mais essas rotas mais bem-sucedidas, levando à convergência para a melhor solução.
Essa representação matemática dos feromônios permite que a ACO equilibre de forma eficaz a exploração e o aproveitamento, pesquisando grandes espaços de solução sem ficar preso em ótimos locais.
Implementação em Python da otimização de colônia de formigas
Vamos tentar um exemplo, usando o ACO para resolver um problema simples: encontrar o caminho mais curto entre pontos em um gráfico.
Essa implementação do ACO simula como as "formigas" artificiais percorrem 20 nós em um gráfico para encontrar o caminho mais curto. Cada formiga começa em um nó aleatório e seleciona seu próximo movimento com base nas trilhas de feromônio e nas distâncias entre os nós. Depois de explorar todos os caminhos, as formigas retornam ao ponto de partida, completando um ciclo completo.
Com o tempo, os feromônios são atualizados: os caminhos mais curtos recebem um reforço maior, enquanto outros evaporam. Esse processo dinâmico permite que o algoritmo converse para uma solução ideal.
import numpy as np
import matplotlib.pyplot as plt
# Graph class represents the environment where ants will travel
class Graph:
def __init__(self, distances):
# Initialize the graph with a distance matrix (distances between nodes)
self.distances = distances
self.num_nodes = len(distances) # Number of nodes (cities)
# Initialize pheromones for each path between nodes (same size as distances)
self.pheromones = np.ones_like(distances, dtype=float) # Start with equal pheromones
# Ant class represents an individual ant that travels across the graph
class Ant:
def __init__(self, graph):
self.graph = graph
# Choose a random starting node for the ant
self.current_node = np.random.randint(graph.num_nodes)
self.path = [self.current_node] # Start path with the initial node
self.total_distance = 0 # Start with zero distance traveled
# Unvisited nodes are all nodes except the starting one
self.unvisited_nodes = set(range(graph.num_nodes)) - {self.current_node}
# Select the next node for the ant to travel to, based on pheromones and distances
def select_next_node(self):
# Initialize an array to store the probability for each node
probabilities = np.zeros(self.graph.num_nodes)
# For each unvisited node, calculate the probability based on pheromones and distances
for node in self.unvisited_nodes:
if self.graph.distances[self.current_node][node] > 0: # Only consider reachable nodes
# The more pheromones and the shorter the distance, the more likely the node will be chosen
probabilities[node] = (self.graph.pheromones[self.current_node][node] ** 2 /
self.graph.distances[self.current_node][node])
probabilities /= probabilities.sum() # Normalize the probabilities to sum to 1
# Choose the next node based on the calculated probabilities
next_node = np.random.choice(range(self.graph.num_nodes), p=probabilities)
return next_node
# Move to the next node and update the ant's path
def move(self):
next_node = self.select_next_node() # Pick the next node
self.path.append(next_node) # Add it to the path
# Add the distance between the current node and the next node to the total distance
self.total_distance += self.graph.distances[self.current_node][next_node]
self.current_node = next_node # Update the current node to the next node
self.unvisited_nodes.remove(next_node) # Mark the next node as visited
# Complete the path by visiting all nodes and returning to the starting node
def complete_path(self):
while self.unvisited_nodes: # While there are still unvisited nodes
self.move() # Keep moving to the next node
# After visiting all nodes, return to the starting node to complete the cycle
self.total_distance += self.graph.distances[self.current_node][self.path[0]]
self.path.append(self.path[0]) # Add the starting node to the end of the path
# ACO (Ant Colony Optimization) class runs the algorithm to find the best path
class ACO:
def __init__(self, graph, num_ants, num_iterations, decay=0.5, alpha=1.0):
self.graph = graph
self.num_ants = num_ants # Number of ants in each iteration
self.num_iterations = num_iterations # Number of iterations
self.decay = decay # Rate at which pheromones evaporate
self.alpha = alpha # Strength of pheromone update
self.best_distance_history = [] # Store the best distance found in each iteration
# Main function to run the ACO algorithm
def run(self):
best_path = None
best_distance = np.inf # Start with a very large number for comparison
# Run the algorithm for the specified number of iterations
for _ in range(self.num_iterations):
ants = [Ant(self.graph) for _ in range(self.num_ants)] # Create a group of ants
for ant in ants:
ant.complete_path() # Let each ant complete its path
# If the current ant's path is shorter than the best one found so far, update the best path
if ant.total_distance < best_distance:
best_path = ant.path
best_distance = ant.total_distance
self.update_pheromones(ants) # Update pheromones based on the ants' paths
self.best_distance_history.append(best_distance) # Save the best distance for each iteration
return best_path, best_distance
# Update the pheromones on the paths after all ants have completed their trips
def update_pheromones(self, ants):
self.graph.pheromones *= self.decay # Reduce pheromones on all paths (evaporation)
# For each ant, increase pheromones on the paths they took, based on how good their path was
for ant in ants:
for i in range(len(ant.path) - 1):
from_node = ant.path[i]
to_node = ant.path[i + 1]
# Update the pheromones inversely proportional to the total distance traveled by the ant
self.graph.pheromones[from_node][to_node] += self.alpha / ant.total_distance
# Generate random distances between nodes (cities) for a 20-node graph
num_nodes = 20
distances = np.random.randint(1, 100, size=(num_nodes, num_nodes)) # Random distances between 1 and 100
np.fill_diagonal(distances, 0) # Distance from a node to itself is 0
graph = Graph(distances) # Create the graph with the random distances
aco = ACO(graph, num_ants=10, num_iterations=30) # Initialize ACO with 10 ants and 30 iterations
best_path, best_distance = aco.run() # Run the ACO algorithm to find the best path
# Print the best path found and the total distance
print(f"Best path: {best_path}")
print(f"Total distance: {best_distance}")
# Plotting the final solution (first plot) - Shows the final path found by the ants
def plot_final_solution(distances, path):
num_nodes = len(distances)
# Generate random coordinates for the nodes to visualize them on a 2D plane
coordinates = np.random.rand(num_nodes, 2) * 10
# Plot the nodes (cities) as red points
plt.scatter(coordinates[:, 0], coordinates[:, 1], color='red')
# Label each node with its index number
for i in range(num_nodes):
plt.text(coordinates[i, 0], coordinates[i, 1], f"{i}", fontsize=10)
# Plot the path (edges) connecting the nodes, showing the best path found
for i in range(len(path) - 1):
start, end = path[i], path[i + 1]
plt.plot([coordinates[start, 0], coordinates[end, 0]],
[coordinates[start, 1], coordinates[end, 1]],
'blue', linewidth=1.5)
plt.title("Final Solution: Best Path")
plt.show()
# Plotting the distance over iterations (second plot) - Shows how the path length improves over time
def plot_distance_over_iterations(best_distance_history):
# Plot the best distance found in each iteration (should decrease over time)
plt.plot(best_distance_history, color='green', linewidth=2)
plt.title("Trip Length Over Iterations")
plt.xlabel("Iteration")
plt.ylabel("Distance")
plt.show()
# Call the plotting functions to display the results
plot_final_solution(distances, best_path)
plot_distance_over_iterations(aco.best_distance_history)![Esse gráfico mostra a solução final, o melhor caminho encontrado, para você viajar para cada nó na menor distância. Nessa execução, a melhor rota encontrada foi [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], com uma distância total de 129.](https://media.datacamp.com/cms/google/ad_4nxcfk4zmpwq-et7v9dapocc9zbf7nm-mukhnmf83ih4ce-kh30kcuds_7ubqjmnv4ncv_iwr2nzg_oandfg1f6jc_wqkgdpu7jxlp4iilaruergyu4polxvvk5gu8x65jnuckjfj6knyoh-yqf8gpn_inper.png)
Esse gráfico mostra a solução final, o melhor caminho encontrado, para que você chegue a cada nó na distância mais curta. Nessa execução, a melhor rota foi encontrada como [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], com uma distância total de 129.
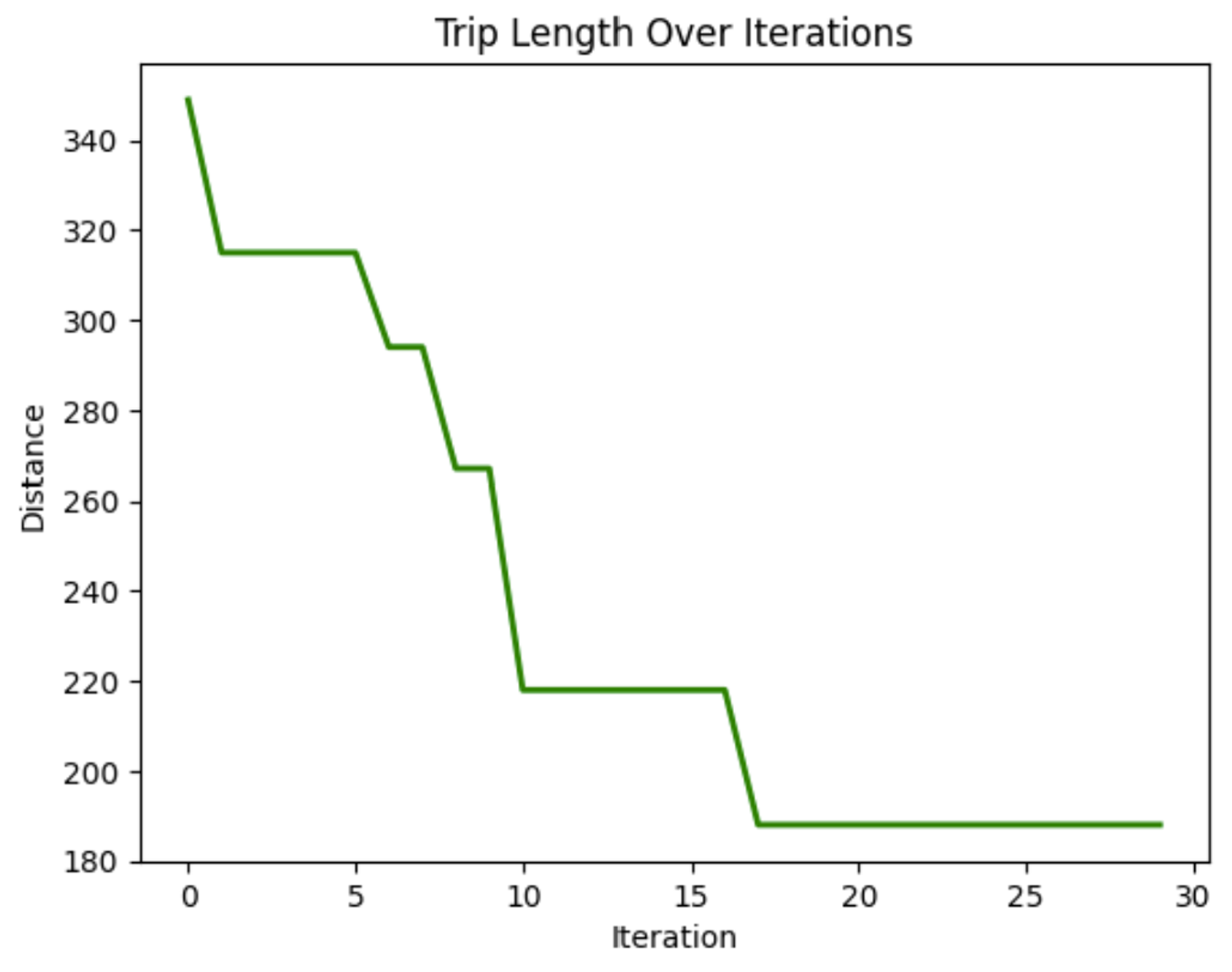
Nesse gráfico, podemos ver que a distância percorrida ao atravessar os nós diminui ao longo das iterações. Isso demonstra que o modelo está melhorando a duração da viagem ao longo do tempo.
Aplicações da otimização de colônias de formigas
A adaptabilidade e a eficiência do ACO fazem dele uma ferramenta poderosa em vários setores. Alguns aplicativos incluem:
- Problemas de roteamento: O ACO é usado para otimizar o roteamento de rede (por exemplo, determinar o caminho mais curto para pacotes de dados em uma rede), transporte e serviços de entrega.
- Agendamento: O ACO pode ser aplicado à programação de tarefas de fabricação ou logística, garantindo que os recursos sejam alocados de forma eficiente.
- Alocação de recursos: O algoritmo pode ser usado para alocar recursos limitados, como no gerenciamento de projetos ou em operações complexas em que diversas variáveis devem ser consideradas.
A força do ACO está em sua capacidade de evoluir e se adaptar, tornando-o adequado para ambientes dinâmicos em que as condições podem mudar, como roteamento de tráfego em tempo real ou planejamento industrial.
Desenvolver aplicativos de IA
Otimização por enxame de partículas (PSO)
A otimização por enxame de partículas (PSO) inspira-se no comportamento de bandos de pássaros e cardumes de peixes. Nesses sistemas naturais, os indivíduos se movem com base em suas próprias experiências anteriores e nas posições de seus vizinhos, ajustando-se gradualmente para seguir os membros mais bem-sucedidos do grupo. O PSO aplica esse conceito a problemas de otimização, em que as partículas, chamadas de agentes, movem-se pelo espaço de pesquisa para encontrar uma solução ideal.
Em comparação com o ACO, o PSO opera em espaços contínuos em vez de discretos. No ACO, o foco está na busca de caminhos e escolhas discretas, enquanto o PSO é mais adequado para problemas que envolvem variáveis contínuas, como o ajuste de parâmetros.
No PSO, as partículas exploram um espaço de pesquisa. Eles ajustam suas posições com base em dois fatores principais: sua posição pessoal mais conhecida e a posição mais conhecida de todo o enxame. Esse mecanismo de feedback duplo permite que eles convirjam para o ótimo global.
Como funciona a otimização por enxame de partículas
O processo começa com um enxame de partículas inicializado aleatoriamente no espaço de solução. Cada partícula representa uma possível solução para o problema de otimização. À medida que as partículas se movem, elas se lembram de suas melhores posições pessoais (a melhor solução que encontraram até o momento) e são atraídas para a melhor posição global (a melhor solução que qualquer partícula encontrou).
Esse movimento é impulsionado por dois fatores: exploração e explotação. A exploração envolve o refinamento da pesquisa em torno da melhor solução atual, enquanto a exploração incentiva as partículas a pesquisar outras partes do espaço de solução para evitar que fiquem presas em ótimos locais. Ao equilibrar essas duas dinâmicas, o PSO converge com eficiência para a melhor solução.
Implementação em Python da otimização por enxame de partículas
Em gerenciamento de portfólio financeiroencontrar a melhor maneira de alocar ativos para obter o máximo de retorno e manter os riscos baixos pode ser complicado. Vamos usar um PSO para descobrir qual combinação de ativos nos dará o maior retorno sobre o investimento.
O código abaixo mostra como o PSO funciona para otimizar uma carteira financeira fictícia. Ele começa com alocações aleatórias de ativos e, em seguida, ajusta-as em várias iterações com base no que funciona melhor, encontrando gradualmente a combinação ideal de ativos para obter o maior retorno com o menor risco.
import numpy as np
import matplotlib.pyplot as plt
# Define the PSO parameters
class Particle:
def __init__(self, n_assets):
# Initialize a particle with random weights and velocities
self.position = np.random.rand(n_assets)
self.position /= np.sum(self.position) # Normalize weights so they sum to 1
self.velocity = np.random.rand(n_assets)
self.best_position = np.copy(self.position)
self.best_score = float('inf') # Start with a very high score
def objective_function(weights, returns, covariance):
"""
Calculate the portfolio's performance.
- weights: Asset weights in the portfolio.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
portfolio_return = np.dot(weights, returns) # Calculate the portfolio return
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(covariance, weights))) # Calculate portfolio risk (standard deviation)
return -portfolio_return / portfolio_risk # We want to maximize return and minimize risk
def update_particles(particles, global_best_position, returns, covariance, w, c1, c2):
"""
Update the position and velocity of each particle.
- particles: List of particle objects.
- global_best_position: Best position found by all particles.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
- w: Inertia weight to control particle's previous velocity effect.
- c1: Cognitive coefficient to pull particles towards their own best position.
- c2: Social coefficient to pull particles towards the global best position.
"""
for particle in particles:
# Random coefficients for velocity update
r1, r2 = np.random.rand(len(particle.position)), np.random.rand(len(particle.position))
# Update velocity
particle.velocity = (w * particle.velocity +
c1 * r1 * (particle.best_position - particle.position) +
c2 * r2 * (global_best_position - particle.position))
# Update position
particle.position += particle.velocity
particle.position = np.clip(particle.position, 0, 1) # Ensure weights are between 0 and 1
particle.position /= np.sum(particle.position) # Normalize weights to sum to 1
# Evaluate the new position
score = objective_function(particle.position, returns, covariance)
if score < particle.best_score:
# Update the particle's best known position and score
particle.best_position = np.copy(particle.position)
particle.best_score = score
def pso_portfolio_optimization(n_particles, n_iterations, returns, covariance):
"""
Perform Particle Swarm Optimization to find the optimal asset weights.
- n_particles: Number of particles in the swarm.
- n_iterations: Number of iterations for the optimization.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
# Initialize particles
particles = [Particle(len(returns)) for _ in range(n_particles)]
# Initialize global best position
global_best_position = np.random.rand(len(returns))
global_best_position /= np.sum(global_best_position)
global_best_score = float('inf')
# PSO parameters
w = 0.5 # Inertia weight: how much particles are influenced by their own direction
c1 = 1.5 # Cognitive coefficient: how well particles learn from their own best solutions
c2 = 0.5 # Social coefficient: how well particles learn from global best solutions
history = [] # To store the best score at each iteration
for _ in range(n_iterations):
update_particles(particles, global_best_position, returns, covariance, w, c1, c2)
for particle in particles:
score = objective_function(particle.position, returns, covariance)
if score < global_best_score:
# Update the global best position and score
global_best_position = np.copy(particle.position)
global_best_score = score
# Store the best score (negative return/risk ratio) for plotting
history.append(-global_best_score)
return global_best_position, history
# Example data for 3 assets
returns = np.array([0.02, 0.28, 0.15]) # Expected returns for each asset
covariance = np.array([[0.1, 0.02, 0.03], # Covariance matrix for asset risks
[0.02, 0.08, 0.04],
[0.03, 0.04, 0.07]])
# Run the PSO algorithm
n_particles = 10 # Number of particles
n_iterations = 10 # Number of iterations
best_weights, optimization_history = pso_portfolio_optimization(n_particles, n_iterations, returns, covariance)
# Plotting the optimization process
plt.figure(figsize=(12, 6))
plt.plot(optimization_history, marker='o')
plt.title('Portfolio Optimization Using PSO')
plt.xlabel('Iteration')
plt.ylabel('Objective Function Value (Negative of Return/Risk Ratio)')
plt.grid(False) # Turn off gridlines
plt.show()
# Display the optimal asset weights
print(f"Optimal Asset Weights: {best_weights}")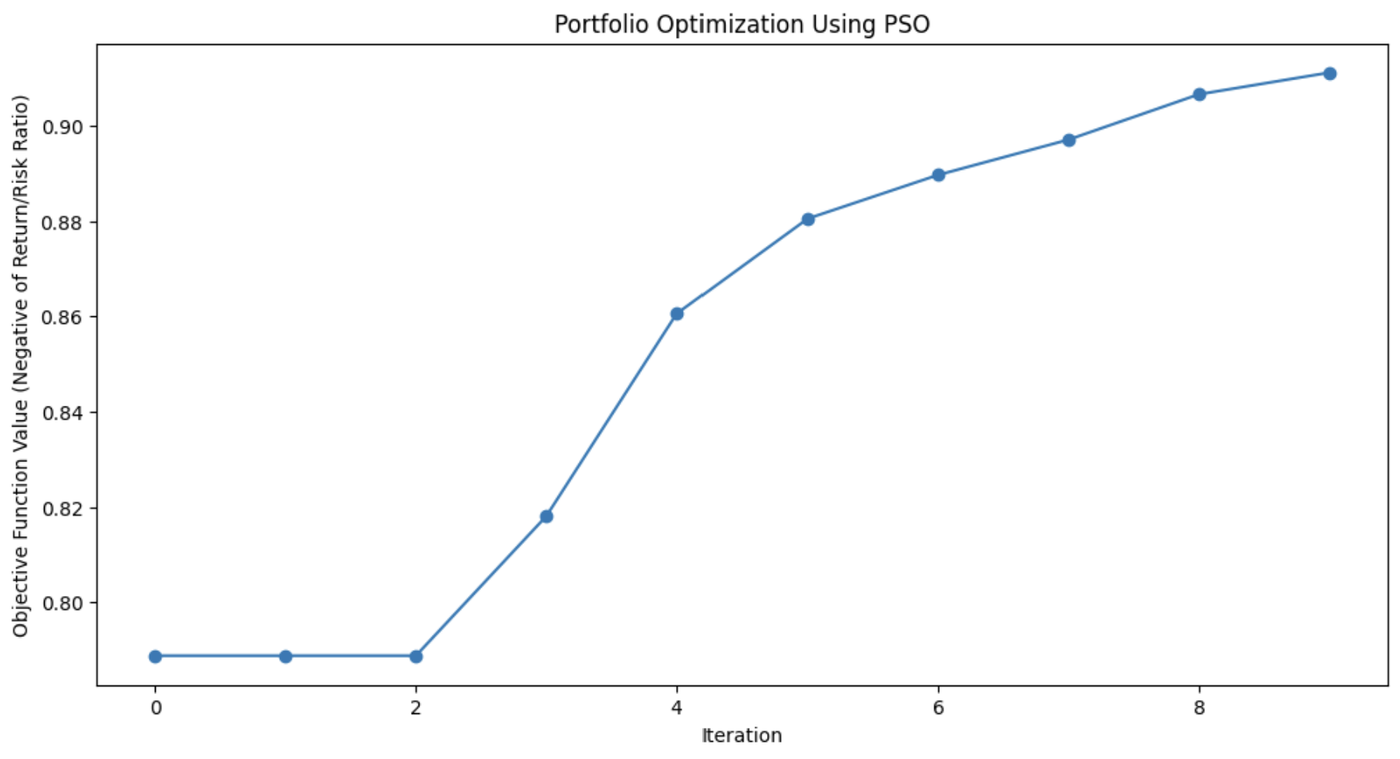
Esse gráfico demonstra o quanto o algoritmo PSO melhorou a combinação de ativos do portfólio a cada iteração.
Aplicações da otimização por enxame de partículas
O PSO é usado por sua simplicidade e eficácia na solução de vários problemas de otimização, especialmente em domínios contínuos. Sua flexibilidade o torna útil para muitos cenários do mundo real em que são necessárias soluções precisas.
Esses aplicativos incluem:
- Aprendizado de máquina: O PSO pode ser aplicado para ajustar hiperparâmetros em algoritmos de aprendizado de máquinaajudando você a encontrar as melhores configurações de modelo.
- Projeto de engenharia: O PSO é útil para otimizar os parâmetros de projeto de sistemas como componentes aeroespaciais ou circuitos elétricos.
- Modelagem financeira: Em finanças, o PSO pode ajudar na otimização do portfólio, minimizando o risco e maximizando os retornos.
A capacidade do PSO de explorar eficientemente os espaços de solução faz com que ele seja aplicável em vários campos, desde a robótica até o gerenciamento de energia e a logística.
Colônia de abelhas artificial (ABC)
O algoritmo de colônia de abelhas artificiais (ABC) é modelado no comportamento de forrageamento das abelhas.
Na natureza, as abelhas buscam fontes de néctar com eficiência e compartilham essas informações com outros membros da colmeia. O ABC captura esse processo de pesquisa colaborativa e o aplica a problemas de otimização, especialmente aqueles que envolvem espaços complexos e de alta dimensão.
O que diferencia o ABC de outros algoritmos de inteligência de enxame é sua capacidade de equilibrar a exploração, concentrando-se no refinamento das soluções atuais, e a exploração, buscando soluções novas e potencialmente melhores. Isso torna o ABC particularmente útil para problemas de grande escala em que a otimização global é fundamental.
Como funciona uma colônia de abelhas artificial
No algoritmo ABC, o enxame de abelhas é dividido em três funções especializadas: abelhas empregadas, observadoras e batedoras. Cada uma dessas funções imita um aspecto diferente de como as abelhas buscam e exploram as fontes de alimento na natureza.
- Abelhas empregadas: Essas abelhas são responsáveis por explorar as fontes de alimento conhecidas, representando as soluções atuais no problema de otimização. Eles avaliam a qualidade (adequação) dessas fontes e compartilham as informações com o restante da colmeia.
- Abelhas observadoras: Depois de coletar informações das abelhas empregadas, os observadores selecionam as fontes de alimento a serem exploradas. Elas baseiam suas escolhas na qualidade das soluções compartilhadas pelas abelhas empregadas, concentrando-se mais nas melhores opções, refinando assim a busca por uma solução ideal.
- Abelhas escoteiras: Quando a fonte de alimento de uma abelha empregada (solução) se esgota ou fica estagnada (quando nenhuma melhoria é encontrada após um determinado número de iterações), a abelha se torna uma batedora. Os escoteiros exploram novas áreas do espaço de solução, procurando fontes de alimento potencialmente inexploradas, injetando assim diversidade no processo de pesquisa.
Essa dinâmica permite que a ABC equilibre a pesquisa entre a exploração intensiva de áreas promissoras e a exploração ampla de novas áreas do espaço de pesquisa. Isso ajuda o algoritmo a evitar ficar preso em ótimos locais e aumenta suas chances de encontrar um ótimo global.
Implementação em Python da colônia de abelhas artificial
A função função Rastrigin é um problema popular em otimização, conhecido por seus inúmeros mínimos locais, o que o torna um desafio difícil para muitos algoritmos. O objetivo é simples: encontrar o mínimo global.
Neste exemplo, usaremos o algoritmo de colônia de abelhas artificiais para resolver esse problema. Cada abelha no algoritmo ABC explora o espaço de pesquisa, procurando soluções melhores para minimizar a função. O código simula abelhas que exploram, exploram e procuram novas áreas, garantindo um equilíbrio entre a exploração e o aproveitamento.
import numpy as np
import matplotlib.pyplot as plt
# Rastrigin function: The objective is to minimize this function
def rastrigin(X):
A = 10
return A * len(X) + sum([(x ** 2 - A * np.cos(2 * np.pi * x)) for x in X])
# Artificial Bee Colony (ABC) algorithm for continuous optimization of Rastrigin function
def artificial_bee_colony_rastrigin(n_iter=100, n_bees=30, dim=2, bound=(-5.12, 5.12)):
"""
Apply Artificial Bee Colony (ABC) algorithm to minimize the Rastrigin function.
Parameters:
n_iter (int): Number of iterations
n_bees (int): Number of bees in the population
dim (int): Number of dimensions (variables)
bound (tuple): Bounds for the search space (min, max)
Returns:
tuple: Best solution found, best fitness value, and list of best fitness values per iteration
"""
# Initialize the bee population with random solutions within the given bounds
bees = np.random.uniform(bound[0], bound[1], (n_bees, dim))
best_bee = bees[0]
best_fitness = rastrigin(best_bee)
best_fitnesses = []
for iteration in range(n_iter):
# Employed bees phase: Explore new solutions based on the current bees
for i in range(n_bees):
# Generate a new candidate solution by perturbing the current bee's position
new_bee = bees[i] + np.random.uniform(-1, 1, dim)
new_bee = np.clip(new_bee, bound[0], bound[1]) # Keep within bounds
# Evaluate the fitness of the new solution
new_fitness = rastrigin(new_bee)
if new_fitness < rastrigin(bees[i]):
bees[i] = new_bee # Update bee if the new solution is better
# Onlooker bees phase: Exploit good solutions
fitnesses = np.array([rastrigin(bee) for bee in bees])
probabilities = 1 / (1 + fitnesses) # Higher fitness gets higher chance
probabilities /= probabilities.sum() # Normalize probabilities
for i in range(n_bees):
if np.random.rand() < probabilities[i]:
selected_bee = bees[i]
# Generate a new candidate solution by perturbing the selected bee
new_bee = selected_bee + np.random.uniform(-0.5, 0.5, dim)
new_bee = np.clip(new_bee, bound[0], bound[1])
if rastrigin(new_bee) < rastrigin(selected_bee):
bees[i] = new_bee
# Scouting phase: Randomly reinitialize some bees to explore new areas
if np.random.rand() < 0.1: # 10% chance to reinitialize a bee
scout_index = np.random.randint(n_bees)
bees[scout_index] = np.random.uniform(bound[0], bound[1], dim)
# Track the best solution found so far
current_best_bee = bees[np.argmin(fitnesses)]
current_best_fitness = min(fitnesses)
if current_best_fitness < best_fitness:
best_fitness = current_best_fitness
best_bee = current_best_bee
best_fitnesses.append(best_fitness)
return best_bee, best_fitness, best_fitnesses
# Apply ABC to minimize the Rastrigin function
best_solution, best_fitness, best_fitnesses = artificial_bee_colony_rastrigin()
# Display results
print("Best Solution (x, y):", best_solution)
print("Best Fitness (Minimum Value):", best_fitness)
# Plot the performance over iterations
plt.figure()
plt.plot(best_fitnesses)
plt.title('Performance of ABC on Rastrigin Function Optimization')
plt.xlabel('Iterations')
plt.ylabel('Best Fitness (Lower is Better)')
plt.grid(True)
plt.show()
# Plot a surface graph of the Rastrigin function
x = np.linspace(-5.12, 5.12, 200)
y = np.linspace(-5.12, 5.12, 200)
X, Y = np.meshgrid(x, y)
Z = 10 * 2 + (X ** 2 - 10 * np.cos(2 * np.pi * X)) + (Y ** 2 - 10 * np.cos(2 * np.pi * Y))
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.colorbar(label='Function Value')
plt.scatter(best_solution[0], best_solution[1], c='red', label='Best Solution')
plt.title('Rastrigin Function Optimization with ABC')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()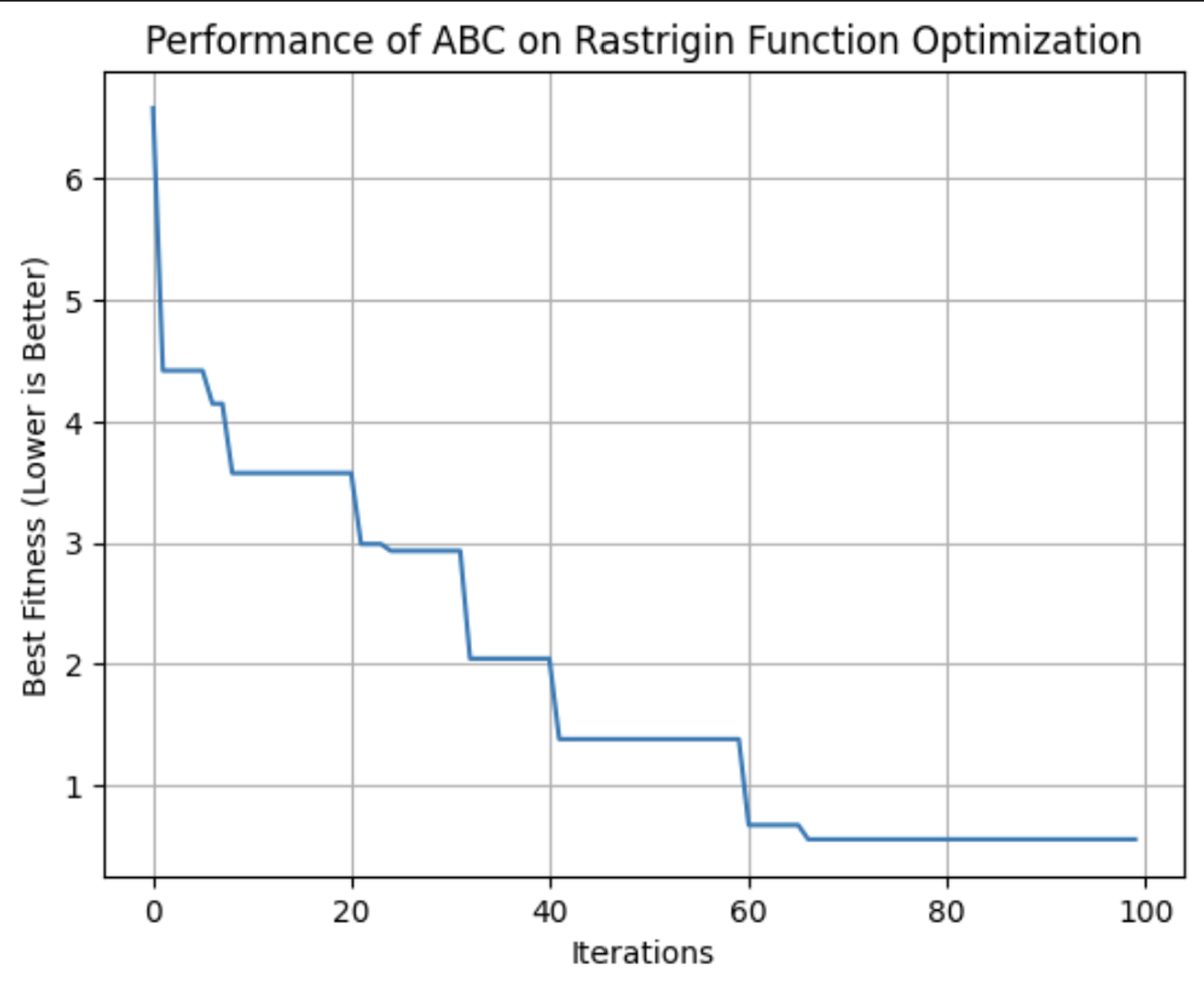
Esse gráfico mostra a adequação da melhor solução encontrada pelo algoritmo ABC a cada iteração. Nessa execução, ele atingiu sua aptidão ideal por volta da 64ª iteração.
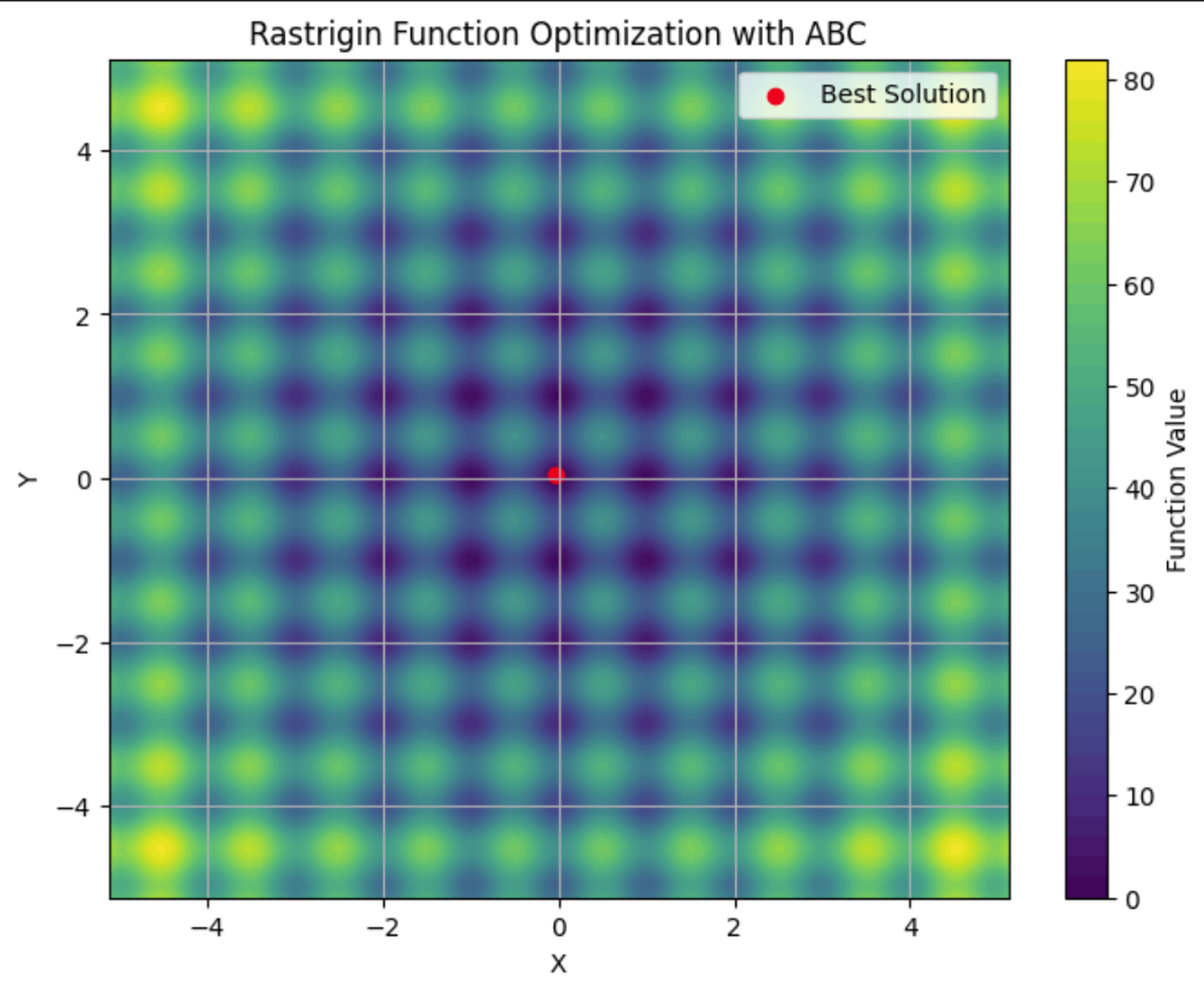
Aqui você pode ver a função Rastrigin plotada em um gráfico de contorno, com seus vários mínimos locais. O ponto vermelho é o mínimo global encontrado pelo algoritmo ABC que executamos.
Aplicações da colônia de abelhas artificial
O algoritmo ABC é uma ferramenta robusta para resolver problemas de otimização. Sua capacidade de explorar com eficiência espaços de pesquisa grandes e complexos faz com que ele seja a escolha ideal para setores em que a adaptabilidade e a escalabilidade são essenciais.
Esses aplicativos incluem:
- Telecomunicações: O ABC pode ser usado para otimizar o posicionamento dos recursos de rede e das antenas, maximizando a cobertura e a intensidade do sinal e minimizando os custos.
- Engenharia: A ABC pode fazer o ajuste fino dos parâmetros na otimização do projeto estrutural.
- Ciência de dados: O ABC pode ser aplicado à seleção de recursos, para identificar as variáveis mais importantes em um conjunto de dados para aprendizado de máquina.
O ABC é um algoritmo flexível adequado para qualquer problema em que seja necessário encontrar soluções ideais em ambientes dinâmicos e de alta dimensão. Sua natureza descentralizada o torna adequado para situações em que outros algoritmos podem ter dificuldades para equilibrar a exploração e o aproveitamento de forma eficiente.
Comparação de algoritmos de inteligência de enxame
Há vários algoritmos de inteligência de enxame, cada um com atributos diferentes. Ao decidir qual usar, é importante pesar seus pontos fortes e fracos para decidir qual atende melhor às suas necessidades.
O ACO é eficaz para problemas combinatórios, como roteamento e programação, mas pode precisar de recursos computacionais significativos. O PSO é mais simples e se destaca na otimização contínua, como o ajuste de hiperparâmetros, mas pode ter dificuldades com os ótimos locais. A ABC equilibra com sucesso a exploração e o aproveitamento, embora exija um ajuste cuidadoso.
Outros algoritmos de inteligência de enxame, como Algoritmo Firefly e Otimização de busca do cucotambém oferecem vantagens exclusivas para tipos específicos de problemas de otimização .
|
Algoritmo |
Pontos fortes |
Pontos fracos |
Bibliotecas preferenciais |
Melhores aplicativos |
|
Otimização por colônia de formigas (ACO) |
Eficaz para problemas combinatórios e lida bem com espaços discretos complexos |
Computacionalmente intensivo e requer ajuste fino |
Problemas de roteamento, programação e alocação de recursos |
|
|
Otimização por enxame de partículas (PSO) |
Bom para otimização contínua e simples e fácil de implementar |
Pode convergir para ótimos locais e é menos eficaz para problemas discretos |
Ajuste de hiperparâmetros, projeto de engenharia, modelagem financeira |
|
|
Colônia de abelhas artificial (ABC) |
Adaptável a problemas grandes e dinâmicos, com exploração e aproveitamento equilibrados |
É computacionalmente intensivo e requer um ajuste cuidadoso dos parâmetros |
Telecomunicações, otimização em larga escala e espaços de alta dimensão |
|
|
Algoritmo Firefly (FA) |
É excelente em otimização multimodal e tem forte capacidade de pesquisa global |
Sensível a configurações de parâmetros e convergência mais lenta |
Processamento de imagens, projeto de engenharia e otimização multimodal |
|
|
Pesquisa de cucos (CS) |
Eficiente na solução de problemas de otimização e com recursos avançados de exploração |
Pode convergir prematuramente e o desempenho depende do ajuste |
Programação, seleção de recursos e aplicativos de engenharia |
Desafios e limitações
Os algoritmos de inteligência de enxame, como muitas técnicas de aprendizado de máquina, enfrentam desafios que podem afetar seu desempenho. Isso inclui:
- Convergência prematura: O enxame pode se estabelecer em uma solução abaixo do ideal muito rapidamente.
- Ajuste de parâmetros: A obtenção de resultados ideais geralmente requer um ajuste cuidadoso das configurações do algoritmo.
- Recursos computacionais e escalabilidade: Esses algoritmos podem ser intensivos em termos de computação, especialmente com problemas maiores e mais complexos, e seu desempenho pode diminuir à medida que a complexidade do problema aumenta. complexidade aumenta.
- Natureza estocástica: A aleatoriedade inerente a esses algoritmos pode levar à variabilidade dos resultados.
Últimas pesquisas e avanços
Uma tendência notável é a integração da inteligência de enxame com outras técnicas de aprendizado de máquina. Os pesquisadores estão explorando como os algoritmos de enxame podem aprimorar tarefas como seleção de recursos e otimização de hiperparâmetros. Confira Um algoritmo híbrido de otimização por enxame de partículas para resolver problemas de engenharia.
Os avanços recentes também se concentram em abordar alguns dos desafios tradicionais associados à inteligência de enxame, como a convergência prematura. Novos algoritmos e técnicas estão sendo desenvolvidos para reduzir o risco de convergir para soluções abaixo do ideal. Para obter mais informações, confira Abordagens baseadas em memória para eliminar a convergência prematura na otimização por enxame de partículas
A escalabilidade é outra área importante de pesquisa. À medida que os problemas se tornam cada vez mais complexos e os volumes de dados aumentam, os pesquisadores estão trabalhando em maneiras de tornar os algoritmos de inteligência de enxame mais dimensionáveis e eficientes. Isso inclui o desenvolvimento de algoritmos que possam lidar com grandes conjuntos de dados e espaços de alta dimensão de forma mais eficaz e, ao mesmo tempo, otimizar os recursos computacionais para reduzir o tempo e o custo associados à execução desses algoritmos. Para saber mais sobre isso, confira Desenvolvimentos recentes na teoria e na aplicabilidade do Swarm Search.
Os algoritmos de enxame estão sendo aplicados a problemas de robóticarobótica, até grandes modelos de linguagem (LLMs), ao diagnóstico médico. Há pesquisa em andamento para saber se esses algoritmos podem ser úteis para ajudar os LLMs a esquecer estrategicamente as informações para cumprir os regulamentosdo Right to Be Forgotten. E, é claro, os algoritmos de enxame têm uma infinidade de aplicações na ciência de dados.
Conclusão
A inteligência de enxame oferece soluções poderosas para problemas de otimização em vários setores. Seus princípios de descentralização, feedback positivo e adaptação permitem que ele lide com tarefas complexas e dinâmicas com as quais os algoritmos tradicionais podem ter dificuldades.
Confira esta análise do estado atual dos algoritmos de enxame, "Swarm intelligence: Uma pesquisa sobre classificação de modelos e aplicativos".
Para se aprofundar nos aplicativos de negócios da IA, confira Estratégia de Inteligência Artificial (IA) ou Inteligência Artificial para Líderes Empresariais. Para saber mais sobre outros algoritmos que imitam a natureza, consulte Genetic Algorithm: Guia completo com implementação em Python.

Sou PhD e tenho 13 anos de experiência trabalhando com dados em um ambiente de pesquisa biológica. Crio software em várias linguagens de programação, incluindo Python, MATLAB e R. Sou apaixonado por compartilhar meu amor pelo aprendizado com o mundo.
