Cursus
Imaginez que vous observez une volée d'oiseaux en plein vol. Il n'y a pas de chef, personne ne donne de directives, et pourtant ils s'élancent et planent ensemble en parfaite harmonie. Cela ressemble à un chaos, mais il y a un ordre caché. Vous pouvez observer le même schéma dans les bancs de poissons qui évitent les prédateurs ou dans les fourmis qui trouvent le chemin le plus court vers la nourriture. Ces créatures s'appuient sur des règles simples et une communication locale pour accomplir des tâches étonnamment complexes sans contrôle central.
C'est la magie de l l'intelligence de l'essaim.
Nous pouvons reproduire ce comportement à l'aide d'algorithmes qui résolvent des problèmes difficiles en imitant l'intelligence en essaim.
Qu'est-ce que l'intelligence en essaim ?
L'intelligence en essaim est une approche informatique qui permet de résoudre des problèmes complexes en imitant le comportement décentralisé et auto-organisé observé dans les essaims naturels tels que les volées d'oiseaux ou les colonies de fourmis.
Examinons deux concepts clés : la décentralisation et le retour d'information positif.
Décentralisation et émergence
Le concept de décentralisation est au cœur de l'intelligence en essaim. Plutôt que de s'en remettre à un chef central pour diriger les actions, chaque individu, ou "agent", agit de manière autonome sur la base d'informations locales limitées.
Cette prise de décision décentralisée conduit à une propriété émergente - un comportement complexe et organisé résultant des interactions simples des agents. Dans les systèmes en essaim, le résultat global, ou la solution, n'est pas préprogrammé mais émerge naturellement de ces actions individuelles.
Prenons l'exemple des fourmis. Lors de la recherche de nourriture, une fourmi explore son environnement au hasard jusqu'à ce qu'elle trouve de la nourriture, puis elle dépose une piste de phéromones sur le chemin du retour vers la colonie. D'autres fourmis rencontrent cette piste et sont plus susceptibles de la suivre, renforçant le chemin si elles trouvent de la nourriture à l'extrémité. Au fil du temps, les itinéraires plus courts ou plus efficaces attirent naturellement plus de fourmis, car des pistes de phéromones plus fortes se forment le long de ces itinéraires. Aucune fourmi ne "connaît" la meilleure route dès le départ, mais collectivement, grâce à des décisions décentralisées et au renforcement des chemins empruntés, la colonie converge vers la solution optimale.
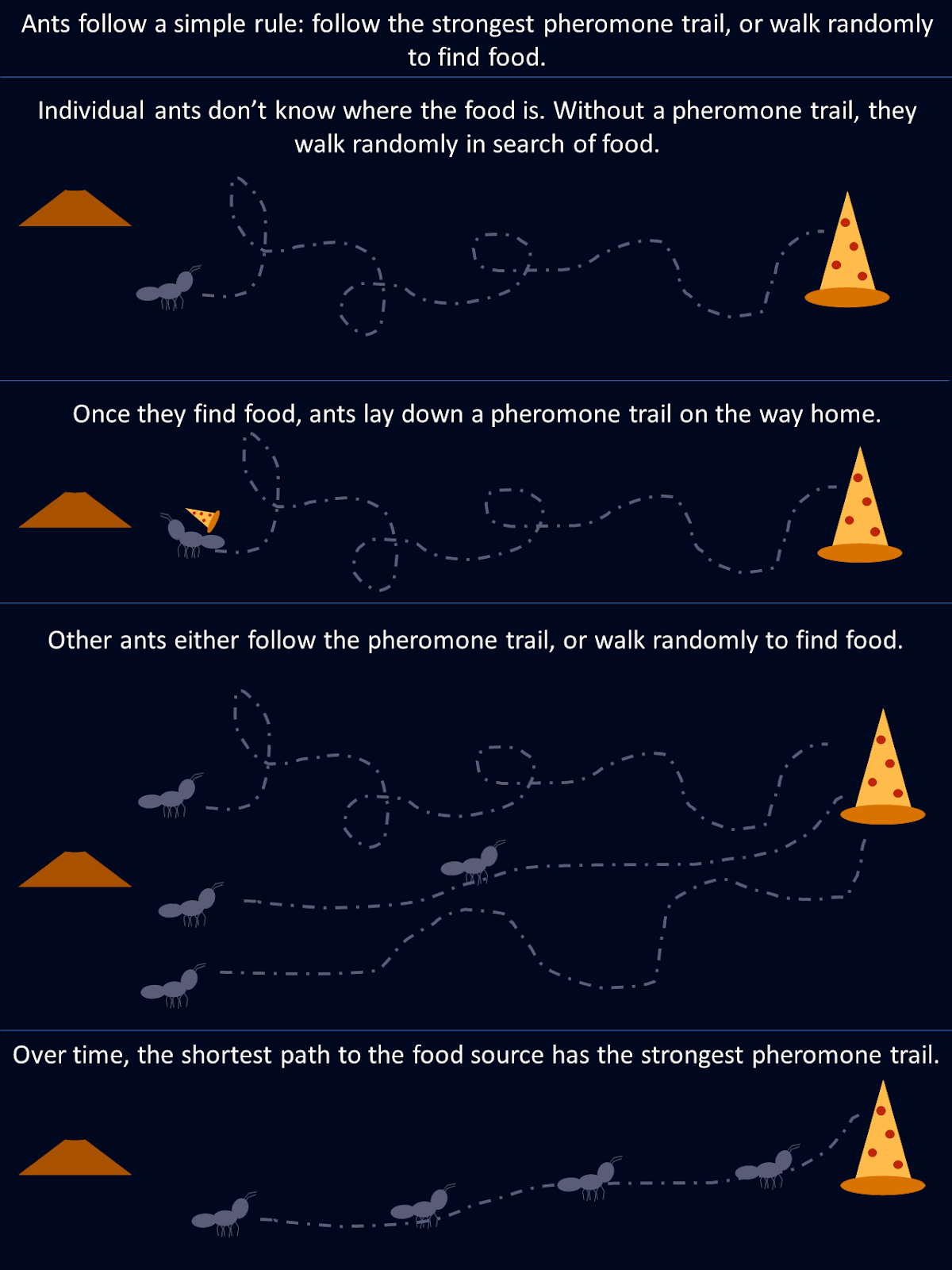
Ce diagramme montre comment des règles simples suivies par des fourmis individuelles aboutissent à une solution optimale pour l'ensemble de la colonie.
Rétroaction positive et adaptation
La rétroaction positive est un mécanisme des systèmes d'intelligence en essaim, où les actions réussies sont récompensées et renforcées. Cela conduit à un processus d'auto-amplification, comme les fourmis qui renforcent les pistes de phéromones le long de chemins de recherche de nourriture plus courts. Ce renforcement des comportements bénéfiques permet à l'essaim d'améliorer ses performances globales au fil du temps.
Dans le domaine de l'intelligence artificielle intelligence artificielleles algorithmes d'intelligence en essaim imitent ce phénomène en ajustant des facteurs clés, tels que les probabilités ou les poids, en fonction de la qualité des solutions trouvées. Au fur et à mesure que de meilleures solutions sont découvertes, les agents s'y intéressent de plus en plus, ce qui accélère le processus de convergence. Cette boucle de rétroaction dynamique permet aux systèmes en essaim de s'adapter à des environnements changeants et d'affiner leurs performances.
Il existe plusieurs algorithmes d'intelligence en essaim qui imitent différents systèmes biologiques. Passons en revue quelques-uns des plus populaires.
Optimisation par colonies de fourmis (ACO)
L'optimisation des colonies de fourmis (ACO) est un algorithme inspiré du comportement de recherche de nourriture des fourmis décrit ci-dessus. Il est conçu pour résoudre les problèmes d'optimisation combinatoire d'optimisation en particulier ceux pour lesquels il faut trouver la meilleure solution possible parmi plusieurs. Un exemple classique est le problème du problème du voyageur de commerceoù l'objectif est de déterminer l'itinéraire le plus court possible pour relier un ensemble de lieux.
Comment fonctionne l'optimisation par colonies de fourmis ?
Dans la nature, les fourmis communiquent en laissant derrière elles des pistes de phéromones, qui indiquent à d'autres fourmis le chemin vers une source de nourriture. Plus les fourmis suivent cette piste, plus elle se renforce. L'ACO imite ce comportement avec des phéromones représentées par des valeurs mathématiques stockées dans une matrice de phéromones. Cette matrice tient compte de la désirabilité des différentes solutions et est mise à jour au fur et à mesure de la progression de l'algorithme.
Dans l'ACO, chaque "fourmi artificielle" représente une solution potentielle au problème, comme un itinéraire dans le problème du voyageur de commerce. L'algorithme commence par la sélection aléatoire de chemins par toutes les fourmis, et les valeurs de phéromones aident à guider les futures fourmis. Ces valeurs sont stockées dans une matrice où chaque entrée correspond au "niveau de phéromone" entre deux points (comme des villes).
- Initialisation : L'algorithme commence par créer un ensemble aléatoire de solutions, les fourmis explorant différents chemins.
- Informations sur les phéromones et les heuristiques : La trajectoire de chaque fourmi est influencée par deux facteurs principaux : les niveaux de phéromones (le degré de "désirabilité" d'une solution sur la base des itérations précédentes) et les informations heuristiques (par exemple, la distance entre deux villes). Plus la valeur de la phéromone est élevée, plus le chemin a de chances d'être choisi.
- Mise à jour des phéromones : Une fois que toutes les fourmis ont terminé leur parcours, les valeurs de la phéromone sont mises à jour. Les chemins qui faisaient partie des meilleures solutions reçoivent des mises à jour de phéromones plus importantes, tandis que ceux qui faisaient partie des solutions sous-optimales subissent une évaporation. Mathématiquement, cela se fait en augmentant les valeurs de phéromone dans la matrice pour les bonnes solutions et en les réduisant au fil du temps pour les autres.
- Convergence : Au cours des itérations successives, la matrice de phéromones évolue pour refléter les meilleures solutions, guidant les fourmis vers des chemins plus solides. Au fur et à mesure que le processus se répète, les fourmis privilégient de plus en plus les itinéraires les plus performants, ce qui conduit à une convergence vers la meilleure solution.
Cette représentation mathématique des phéromones permet à l'ACO d'équilibrer efficacement l'exploration et l'exploitation, en recherchant de vastes espaces de solution sans rester bloqué dans des optima locaux.
Optimisation par colonies de fourmis Mise en œuvre Python
Prenons un exemple en utilisant l'ACO pour résoudre un problème simple : trouver le chemin le plus court entre deux points d'un graphe.
Cette implémentation de l'ACO simule la façon dont des "fourmis" artificielles parcourent 20 nœuds d'un graphe pour trouver le chemin le plus court. Chaque fourmi commence par un nœud aléatoire et choisit son prochain déplacement en fonction des pistes de phéromones et des distances entre les nœuds. Après avoir exploré tous les chemins, les fourmis reviennent à leur point de départ, effectuant ainsi une boucle complète.
Au fil du temps, les phéromones sont mises à jour : les chemins les plus courts sont renforcés, tandis que les autres s'évaporent. Ce processus dynamique permet à l'algorithme de converger vers une solution optimale.
import numpy as np
import matplotlib.pyplot as plt
# Graph class represents the environment where ants will travel
class Graph:
def __init__(self, distances):
# Initialize the graph with a distance matrix (distances between nodes)
self.distances = distances
self.num_nodes = len(distances) # Number of nodes (cities)
# Initialize pheromones for each path between nodes (same size as distances)
self.pheromones = np.ones_like(distances, dtype=float) # Start with equal pheromones
# Ant class represents an individual ant that travels across the graph
class Ant:
def __init__(self, graph):
self.graph = graph
# Choose a random starting node for the ant
self.current_node = np.random.randint(graph.num_nodes)
self.path = [self.current_node] # Start path with the initial node
self.total_distance = 0 # Start with zero distance traveled
# Unvisited nodes are all nodes except the starting one
self.unvisited_nodes = set(range(graph.num_nodes)) - {self.current_node}
# Select the next node for the ant to travel to, based on pheromones and distances
def select_next_node(self):
# Initialize an array to store the probability for each node
probabilities = np.zeros(self.graph.num_nodes)
# For each unvisited node, calculate the probability based on pheromones and distances
for node in self.unvisited_nodes:
if self.graph.distances[self.current_node][node] > 0: # Only consider reachable nodes
# The more pheromones and the shorter the distance, the more likely the node will be chosen
probabilities[node] = (self.graph.pheromones[self.current_node][node] ** 2 /
self.graph.distances[self.current_node][node])
probabilities /= probabilities.sum() # Normalize the probabilities to sum to 1
# Choose the next node based on the calculated probabilities
next_node = np.random.choice(range(self.graph.num_nodes), p=probabilities)
return next_node
# Move to the next node and update the ant's path
def move(self):
next_node = self.select_next_node() # Pick the next node
self.path.append(next_node) # Add it to the path
# Add the distance between the current node and the next node to the total distance
self.total_distance += self.graph.distances[self.current_node][next_node]
self.current_node = next_node # Update the current node to the next node
self.unvisited_nodes.remove(next_node) # Mark the next node as visited
# Complete the path by visiting all nodes and returning to the starting node
def complete_path(self):
while self.unvisited_nodes: # While there are still unvisited nodes
self.move() # Keep moving to the next node
# After visiting all nodes, return to the starting node to complete the cycle
self.total_distance += self.graph.distances[self.current_node][self.path[0]]
self.path.append(self.path[0]) # Add the starting node to the end of the path
# ACO (Ant Colony Optimization) class runs the algorithm to find the best path
class ACO:
def __init__(self, graph, num_ants, num_iterations, decay=0.5, alpha=1.0):
self.graph = graph
self.num_ants = num_ants # Number of ants in each iteration
self.num_iterations = num_iterations # Number of iterations
self.decay = decay # Rate at which pheromones evaporate
self.alpha = alpha # Strength of pheromone update
self.best_distance_history = [] # Store the best distance found in each iteration
# Main function to run the ACO algorithm
def run(self):
best_path = None
best_distance = np.inf # Start with a very large number for comparison
# Run the algorithm for the specified number of iterations
for _ in range(self.num_iterations):
ants = [Ant(self.graph) for _ in range(self.num_ants)] # Create a group of ants
for ant in ants:
ant.complete_path() # Let each ant complete its path
# If the current ant's path is shorter than the best one found so far, update the best path
if ant.total_distance < best_distance:
best_path = ant.path
best_distance = ant.total_distance
self.update_pheromones(ants) # Update pheromones based on the ants' paths
self.best_distance_history.append(best_distance) # Save the best distance for each iteration
return best_path, best_distance
# Update the pheromones on the paths after all ants have completed their trips
def update_pheromones(self, ants):
self.graph.pheromones *= self.decay # Reduce pheromones on all paths (evaporation)
# For each ant, increase pheromones on the paths they took, based on how good their path was
for ant in ants:
for i in range(len(ant.path) - 1):
from_node = ant.path[i]
to_node = ant.path[i + 1]
# Update the pheromones inversely proportional to the total distance traveled by the ant
self.graph.pheromones[from_node][to_node] += self.alpha / ant.total_distance
# Generate random distances between nodes (cities) for a 20-node graph
num_nodes = 20
distances = np.random.randint(1, 100, size=(num_nodes, num_nodes)) # Random distances between 1 and 100
np.fill_diagonal(distances, 0) # Distance from a node to itself is 0
graph = Graph(distances) # Create the graph with the random distances
aco = ACO(graph, num_ants=10, num_iterations=30) # Initialize ACO with 10 ants and 30 iterations
best_path, best_distance = aco.run() # Run the ACO algorithm to find the best path
# Print the best path found and the total distance
print(f"Best path: {best_path}")
print(f"Total distance: {best_distance}")
# Plotting the final solution (first plot) - Shows the final path found by the ants
def plot_final_solution(distances, path):
num_nodes = len(distances)
# Generate random coordinates for the nodes to visualize them on a 2D plane
coordinates = np.random.rand(num_nodes, 2) * 10
# Plot the nodes (cities) as red points
plt.scatter(coordinates[:, 0], coordinates[:, 1], color='red')
# Label each node with its index number
for i in range(num_nodes):
plt.text(coordinates[i, 0], coordinates[i, 1], f"{i}", fontsize=10)
# Plot the path (edges) connecting the nodes, showing the best path found
for i in range(len(path) - 1):
start, end = path[i], path[i + 1]
plt.plot([coordinates[start, 0], coordinates[end, 0]],
[coordinates[start, 1], coordinates[end, 1]],
'blue', linewidth=1.5)
plt.title("Final Solution: Best Path")
plt.show()
# Plotting the distance over iterations (second plot) - Shows how the path length improves over time
def plot_distance_over_iterations(best_distance_history):
# Plot the best distance found in each iteration (should decrease over time)
plt.plot(best_distance_history, color='green', linewidth=2)
plt.title("Trip Length Over Iterations")
plt.xlabel("Iteration")
plt.ylabel("Distance")
plt.show()
# Call the plotting functions to display the results
plot_final_solution(distances, best_path)
plot_distance_over_iterations(aco.best_distance_history)![Ce graphique montre la solution finale, le meilleur chemin trouvé, pour se rendre à chaque nœud sur la distance la plus courte. Dans cette exécution, le meilleur chemin est [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], avec une distance totale de 129.](https://media.datacamp.com/cms/google/ad_4nxcfk4zmpwq-et7v9dapocc9zbf7nm-mukhnmf83ih4ce-kh30kcuds_7ubqjmnv4ncv_iwr2nzg_oandfg1f6jc_wqkgdpu7jxlp4iilaruergyu4polxvvk5gu8x65jnuckjfj6knyoh-yqf8gpn_inper.png)
Ce graphique montre la solution finale, le meilleur chemin trouvé, pour se rendre à chaque nœud en parcourant la distance la plus courte. Dans ce cas, le meilleur itinéraire est [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], avec une distance totale de 129.
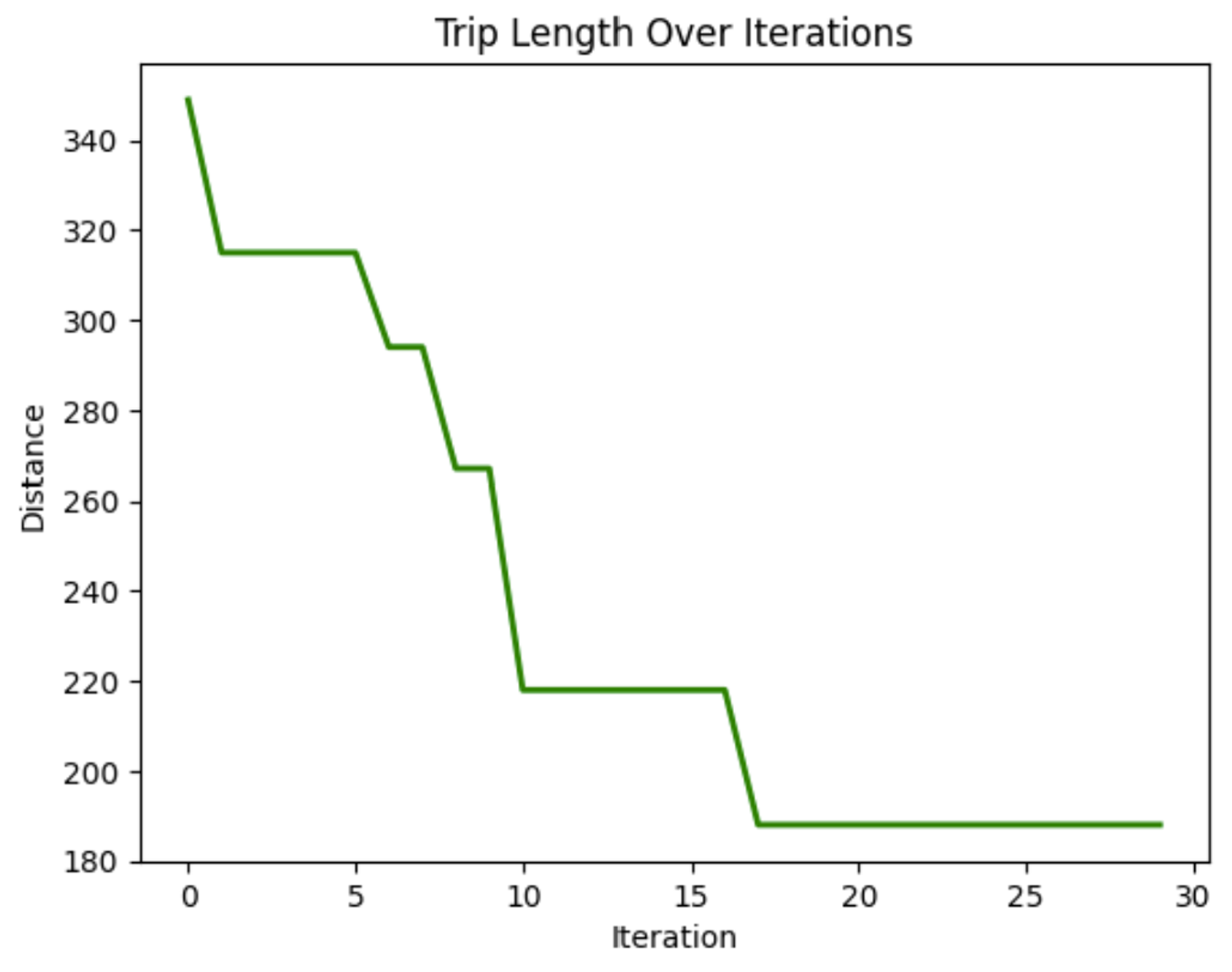
Dans ce graphique, nous pouvons voir que la distance parcourue en traversant les nœuds diminue au fil des itérations. Cela prouve que le modèle améliore la longueur des trajets au fil du temps.
Applications de l'optimisation par colonies de fourmis
L'adaptabilité et l'efficacité de l'ACO en font un outil puissant dans divers secteurs. Voici quelques exemples d'applications :
- Problèmes de routage : L'ACO est utilisé pour optimiser le routage des réseaux (par exemple, déterminer le chemin le plus court pour les paquets de données dans un réseau), le transport et les services de livraison.
- Programmation : L'ACO peut être appliqué à l'ordonnancement des tâches dans la fabrication ou la logistique, en veillant à ce que les ressources soient allouées de manière efficace.
- Allocation des ressources : L'algorithme peut être utilisé pour allouer des ressources limitées, par exemple dans le cadre de la gestion de projets ou d'opérations complexes où de multiples variables doivent être prises en compte.
La force de l'ACO réside dans sa capacité à évoluer et à s'adapter, ce qui la rend appropriée pour les environnements dynamiques où les conditions peuvent changer, tels que l'acheminement du trafic en temps réel ou la planification industrielle.
Développer des applications d'IA
Optimisation par essaims de particules (PSO)
L'optimisation par essaims de particules (PSO) s'inspire du comportement des volées d'oiseaux et des bancs de poissons. Dans ces systèmes naturels, les individus se déplacent en fonction de leurs expériences antérieures et des positions de leurs voisins, s'adaptant progressivement pour suivre les membres les plus performants du groupe. L'OPS applique ce concept aux problèmes d'optimisation, où les particules, appelées agents, se déplacent dans l'espace de recherche pour trouver une solution optimale.
Par rapport à ACO, PSO fonctionne dans des espaces continus plutôt que discrets. Dans l'ACO, l'accent est mis sur la recherche de chemins et les choix discrets, tandis que le PSO est mieux adapté aux problèmes impliquant des variables continues, tels que l'ajustement des paramètres.
Dans l'OSP, les particules explorent un espace de recherche. Ils ajustent leur position en fonction de deux facteurs principaux : leur position personnelle la plus connue et la position la plus connue de l'ensemble de l'essaim. Ce double mécanisme de rétroaction leur permet de converger vers l'optimum global.
Comment fonctionne l'optimisation par essaims de particules
Le processus commence par un essaim de particules initialisé de manière aléatoire dans l'espace de solution. Chaque particule représente une solution possible au problème d'optimisation. Lorsque les particules se déplacent, elles se souviennent de leur meilleure position personnelle (la meilleure solution qu'elles ont rencontrée jusqu'à présent) et sont attirées vers la meilleure position globale (la meilleure solution que toutes les particules ont trouvée).
Ce mouvement est motivé par deux facteurs : l'exploitation et l'exploration. L'exploitation consiste à affiner la recherche autour de la meilleure solution actuelle, tandis que l'exploration encourage les particules à rechercher d'autres parties de l'espace de solution pour éviter de rester bloquées dans des optima locaux. En équilibrant ces deux dynamiques, PSO converge efficacement vers la meilleure solution.
Optimisation par essaims de particules : implémentation Python
Dans le domaine de la gestion de portefeuille financieril peut être difficile de trouver la meilleure façon d'allouer les actifs pour obtenir les meilleurs rendements tout en maintenant les risques à un niveau bas. Utilisons une OSP pour trouver la combinaison d'actifs qui nous donnera le meilleur retour sur investissement.
Le code ci-dessous montre comment PSO fonctionne pour optimiser un portefeuille financier fictif. Il commence par des répartitions d'actifs aléatoires, puis les modifie au cours de plusieurs itérations sur la base de ce qui fonctionne le mieux, pour trouver progressivement la combinaison optimale d'actifs permettant d'obtenir le rendement le plus élevé avec le risque le plus faible.
import numpy as np
import matplotlib.pyplot as plt
# Define the PSO parameters
class Particle:
def __init__(self, n_assets):
# Initialize a particle with random weights and velocities
self.position = np.random.rand(n_assets)
self.position /= np.sum(self.position) # Normalize weights so they sum to 1
self.velocity = np.random.rand(n_assets)
self.best_position = np.copy(self.position)
self.best_score = float('inf') # Start with a very high score
def objective_function(weights, returns, covariance):
"""
Calculate the portfolio's performance.
- weights: Asset weights in the portfolio.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
portfolio_return = np.dot(weights, returns) # Calculate the portfolio return
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(covariance, weights))) # Calculate portfolio risk (standard deviation)
return -portfolio_return / portfolio_risk # We want to maximize return and minimize risk
def update_particles(particles, global_best_position, returns, covariance, w, c1, c2):
"""
Update the position and velocity of each particle.
- particles: List of particle objects.
- global_best_position: Best position found by all particles.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
- w: Inertia weight to control particle's previous velocity effect.
- c1: Cognitive coefficient to pull particles towards their own best position.
- c2: Social coefficient to pull particles towards the global best position.
"""
for particle in particles:
# Random coefficients for velocity update
r1, r2 = np.random.rand(len(particle.position)), np.random.rand(len(particle.position))
# Update velocity
particle.velocity = (w * particle.velocity +
c1 * r1 * (particle.best_position - particle.position) +
c2 * r2 * (global_best_position - particle.position))
# Update position
particle.position += particle.velocity
particle.position = np.clip(particle.position, 0, 1) # Ensure weights are between 0 and 1
particle.position /= np.sum(particle.position) # Normalize weights to sum to 1
# Evaluate the new position
score = objective_function(particle.position, returns, covariance)
if score < particle.best_score:
# Update the particle's best known position and score
particle.best_position = np.copy(particle.position)
particle.best_score = score
def pso_portfolio_optimization(n_particles, n_iterations, returns, covariance):
"""
Perform Particle Swarm Optimization to find the optimal asset weights.
- n_particles: Number of particles in the swarm.
- n_iterations: Number of iterations for the optimization.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
# Initialize particles
particles = [Particle(len(returns)) for _ in range(n_particles)]
# Initialize global best position
global_best_position = np.random.rand(len(returns))
global_best_position /= np.sum(global_best_position)
global_best_score = float('inf')
# PSO parameters
w = 0.5 # Inertia weight: how much particles are influenced by their own direction
c1 = 1.5 # Cognitive coefficient: how well particles learn from their own best solutions
c2 = 0.5 # Social coefficient: how well particles learn from global best solutions
history = [] # To store the best score at each iteration
for _ in range(n_iterations):
update_particles(particles, global_best_position, returns, covariance, w, c1, c2)
for particle in particles:
score = objective_function(particle.position, returns, covariance)
if score < global_best_score:
# Update the global best position and score
global_best_position = np.copy(particle.position)
global_best_score = score
# Store the best score (negative return/risk ratio) for plotting
history.append(-global_best_score)
return global_best_position, history
# Example data for 3 assets
returns = np.array([0.02, 0.28, 0.15]) # Expected returns for each asset
covariance = np.array([[0.1, 0.02, 0.03], # Covariance matrix for asset risks
[0.02, 0.08, 0.04],
[0.03, 0.04, 0.07]])
# Run the PSO algorithm
n_particles = 10 # Number of particles
n_iterations = 10 # Number of iterations
best_weights, optimization_history = pso_portfolio_optimization(n_particles, n_iterations, returns, covariance)
# Plotting the optimization process
plt.figure(figsize=(12, 6))
plt.plot(optimization_history, marker='o')
plt.title('Portfolio Optimization Using PSO')
plt.xlabel('Iteration')
plt.ylabel('Objective Function Value (Negative of Return/Risk Ratio)')
plt.grid(False) # Turn off gridlines
plt.show()
# Display the optimal asset weights
print(f"Optimal Asset Weights: {best_weights}")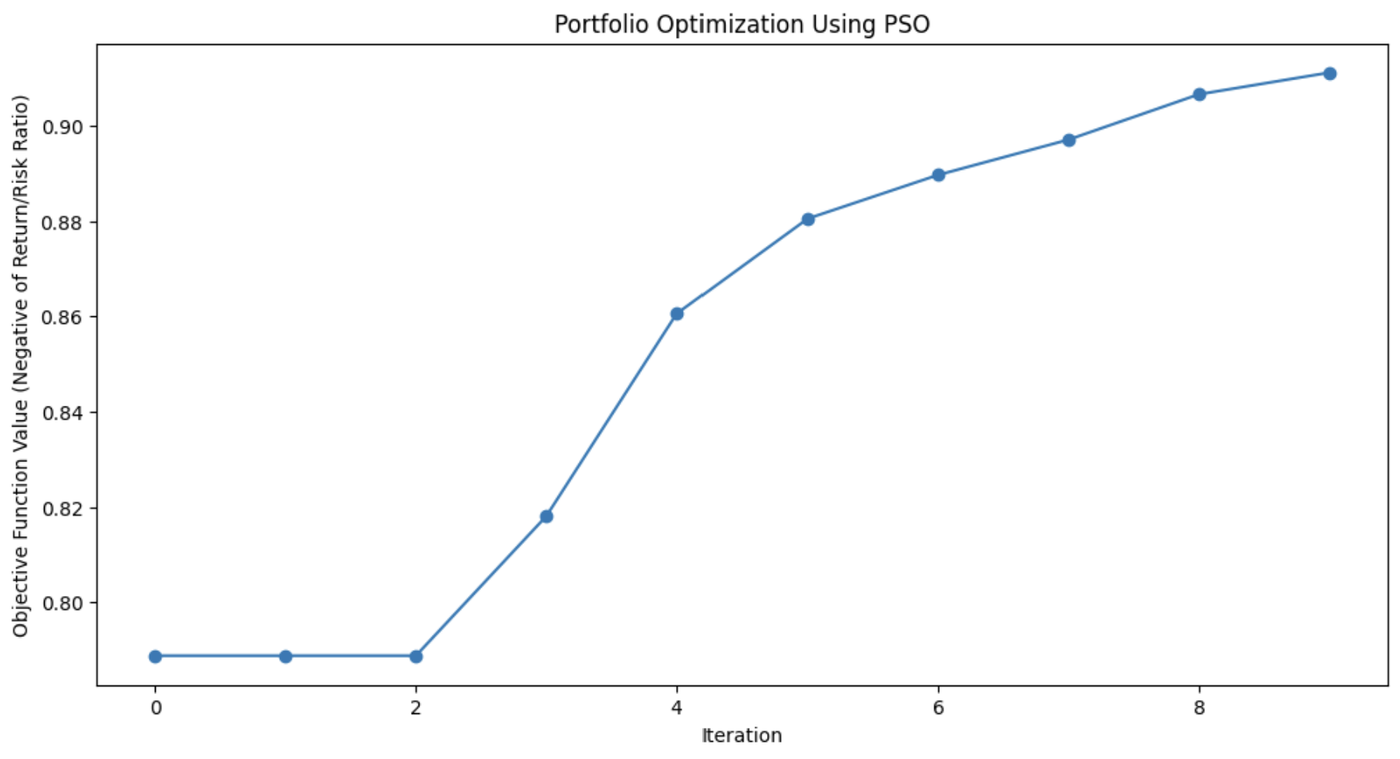
Ce graphique montre à quel point l'algorithme PSO a amélioré la répartition des actifs du portefeuille à chaque itération.
Applications de l'optimisation par essaims de particules
Le PSO est utilisé pour sa simplicité et son efficacité dans la résolution de divers problèmes d'optimisation, en particulier dans les domaines continus. Sa flexibilité le rend utile pour de nombreux scénarios du monde réel où des solutions précises sont nécessaires.
Ces applications sont les suivantes
- Apprentissage automatique: L'OSP peut être appliquée pour régler les hyperparamètres dans les algorithmes d'apprentissage automatique. algorithmes d'apprentissage automatiquece qui permet de trouver les meilleures configurations de modèles.
- Conception technique: L'OSP est utile pour optimiser les paramètres de conception de systèmes tels que les composants aérospatiaux ou les circuits électriques.
- Modélisation financière: En finance, l'OSP peut contribuer à l'optimisation du portefeuille, en minimisant le risque tout en maximisant le rendement.
La capacité de l'OSP à explorer efficacement les espaces de solution la rend applicable à tous les domaines, de la robotique à la gestion de l'énergie en passant par la logistique.
Colonie d'abeilles artificielle (ABC)
L'algorithme de la colonie d'abeilles artificielle (ABC) s'inspire du comportement de recherche de nourriture des abeilles.
Dans la nature, les abeilles mellifères recherchent efficacement les sources de nectar et partagent ces informations avec les autres membres de la ruche. ABC capture ce processus de recherche collaborative et l'applique aux problèmes d'optimisation, en particulier ceux qui impliquent des espaces complexes à haute dimension.
Ce qui distingue l'ABC des autres algorithmes d'intelligence en essaim, c'est sa capacité à équilibrer l'exploitation, en se concentrant sur l'affinement des solutions actuelles, et l'exploration, en recherchant de nouvelles solutions potentiellement meilleures. L'ABC est donc particulièrement utile pour les problèmes à grande échelle où l'optimisation globale est essentielle.
Comment fonctionne une colonie d'abeilles artificielle
Dans l'algorithme ABC, l'essaim d'abeilles est divisé en trois rôles spécialisés : les abeilles employées, les observatrices et les éclaireuses. Chacun de ces rôles imite un aspect différent de la manière dont les abeilles recherchent et exploitent les sources de nourriture dans la nature.
- Abeilles employées: Ces abeilles sont chargées d'explorer les sources de nourriture connues, représentant les solutions actuelles du problème d'optimisation. Elles évaluent la qualité (fitness) de ces sources et partagent l'information avec le reste de la ruche.
- Abeilles non voyantes: Après avoir recueilli des informations auprès des abeilles employées, les spectateurs choisissent les sources de nourriture à explorer plus avant. Elles basent leurs choix sur la qualité des solutions partagées par les abeilles employées, se concentrant davantage sur les meilleures options, affinant ainsi la recherche d'une solution optimale.
- Abeilles scoutes: Lorsque la source de nourriture (solution) d'une abeille employée s'épuise ou stagne (lorsqu'aucune amélioration n'est trouvée après un certain nombre d'itérations), l'abeille devient un éclaireur. Les scouts explorent de nouvelles zones de l'espace de solution, à la recherche de sources de nourriture potentiellement inexplorées, injectant ainsi de la diversité dans le processus de recherche.
Cette dynamique permet à l'ABC d'équilibrer la recherche entre l'exploration intensive de domaines prometteurs et l'exploration large de nouveaux domaines de l'espace de recherche. Cela permet à l'algorithme d'éviter d'être piégé dans des optima locaux et d'augmenter ses chances de trouver un optimum global.
Colonie d'abeilles artificielle Mise en œuvre Python
La fonction fonction de Rastrigin est un problème d'optimisation populaire, connu pour ses nombreux minima locaux, ce qui en fait un défi difficile à relever pour de nombreux algorithmes. L'objectif est simple : trouver le minimum global.
Dans cet exemple, nous utiliserons l'algorithme de la colonie d'abeilles artificielle pour résoudre ce problème. Chaque abeille de l'algorithme ABC explore l'espace de recherche, à la recherche de meilleures solutions pour minimiser la fonction. Le code simule des abeilles qui explorent, exploitent et repèrent de nouvelles zones, assurant un équilibre entre l'exploration et l'exploitation.
import numpy as np
import matplotlib.pyplot as plt
# Rastrigin function: The objective is to minimize this function
def rastrigin(X):
A = 10
return A * len(X) + sum([(x ** 2 - A * np.cos(2 * np.pi * x)) for x in X])
# Artificial Bee Colony (ABC) algorithm for continuous optimization of Rastrigin function
def artificial_bee_colony_rastrigin(n_iter=100, n_bees=30, dim=2, bound=(-5.12, 5.12)):
"""
Apply Artificial Bee Colony (ABC) algorithm to minimize the Rastrigin function.
Parameters:
n_iter (int): Number of iterations
n_bees (int): Number of bees in the population
dim (int): Number of dimensions (variables)
bound (tuple): Bounds for the search space (min, max)
Returns:
tuple: Best solution found, best fitness value, and list of best fitness values per iteration
"""
# Initialize the bee population with random solutions within the given bounds
bees = np.random.uniform(bound[0], bound[1], (n_bees, dim))
best_bee = bees[0]
best_fitness = rastrigin(best_bee)
best_fitnesses = []
for iteration in range(n_iter):
# Employed bees phase: Explore new solutions based on the current bees
for i in range(n_bees):
# Generate a new candidate solution by perturbing the current bee's position
new_bee = bees[i] + np.random.uniform(-1, 1, dim)
new_bee = np.clip(new_bee, bound[0], bound[1]) # Keep within bounds
# Evaluate the fitness of the new solution
new_fitness = rastrigin(new_bee)
if new_fitness < rastrigin(bees[i]):
bees[i] = new_bee # Update bee if the new solution is better
# Onlooker bees phase: Exploit good solutions
fitnesses = np.array([rastrigin(bee) for bee in bees])
probabilities = 1 / (1 + fitnesses) # Higher fitness gets higher chance
probabilities /= probabilities.sum() # Normalize probabilities
for i in range(n_bees):
if np.random.rand() < probabilities[i]:
selected_bee = bees[i]
# Generate a new candidate solution by perturbing the selected bee
new_bee = selected_bee + np.random.uniform(-0.5, 0.5, dim)
new_bee = np.clip(new_bee, bound[0], bound[1])
if rastrigin(new_bee) < rastrigin(selected_bee):
bees[i] = new_bee
# Scouting phase: Randomly reinitialize some bees to explore new areas
if np.random.rand() < 0.1: # 10% chance to reinitialize a bee
scout_index = np.random.randint(n_bees)
bees[scout_index] = np.random.uniform(bound[0], bound[1], dim)
# Track the best solution found so far
current_best_bee = bees[np.argmin(fitnesses)]
current_best_fitness = min(fitnesses)
if current_best_fitness < best_fitness:
best_fitness = current_best_fitness
best_bee = current_best_bee
best_fitnesses.append(best_fitness)
return best_bee, best_fitness, best_fitnesses
# Apply ABC to minimize the Rastrigin function
best_solution, best_fitness, best_fitnesses = artificial_bee_colony_rastrigin()
# Display results
print("Best Solution (x, y):", best_solution)
print("Best Fitness (Minimum Value):", best_fitness)
# Plot the performance over iterations
plt.figure()
plt.plot(best_fitnesses)
plt.title('Performance of ABC on Rastrigin Function Optimization')
plt.xlabel('Iterations')
plt.ylabel('Best Fitness (Lower is Better)')
plt.grid(True)
plt.show()
# Plot a surface graph of the Rastrigin function
x = np.linspace(-5.12, 5.12, 200)
y = np.linspace(-5.12, 5.12, 200)
X, Y = np.meshgrid(x, y)
Z = 10 * 2 + (X ** 2 - 10 * np.cos(2 * np.pi * X)) + (Y ** 2 - 10 * np.cos(2 * np.pi * Y))
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.colorbar(label='Function Value')
plt.scatter(best_solution[0], best_solution[1], c='red', label='Best Solution')
plt.title('Rastrigin Function Optimization with ABC')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()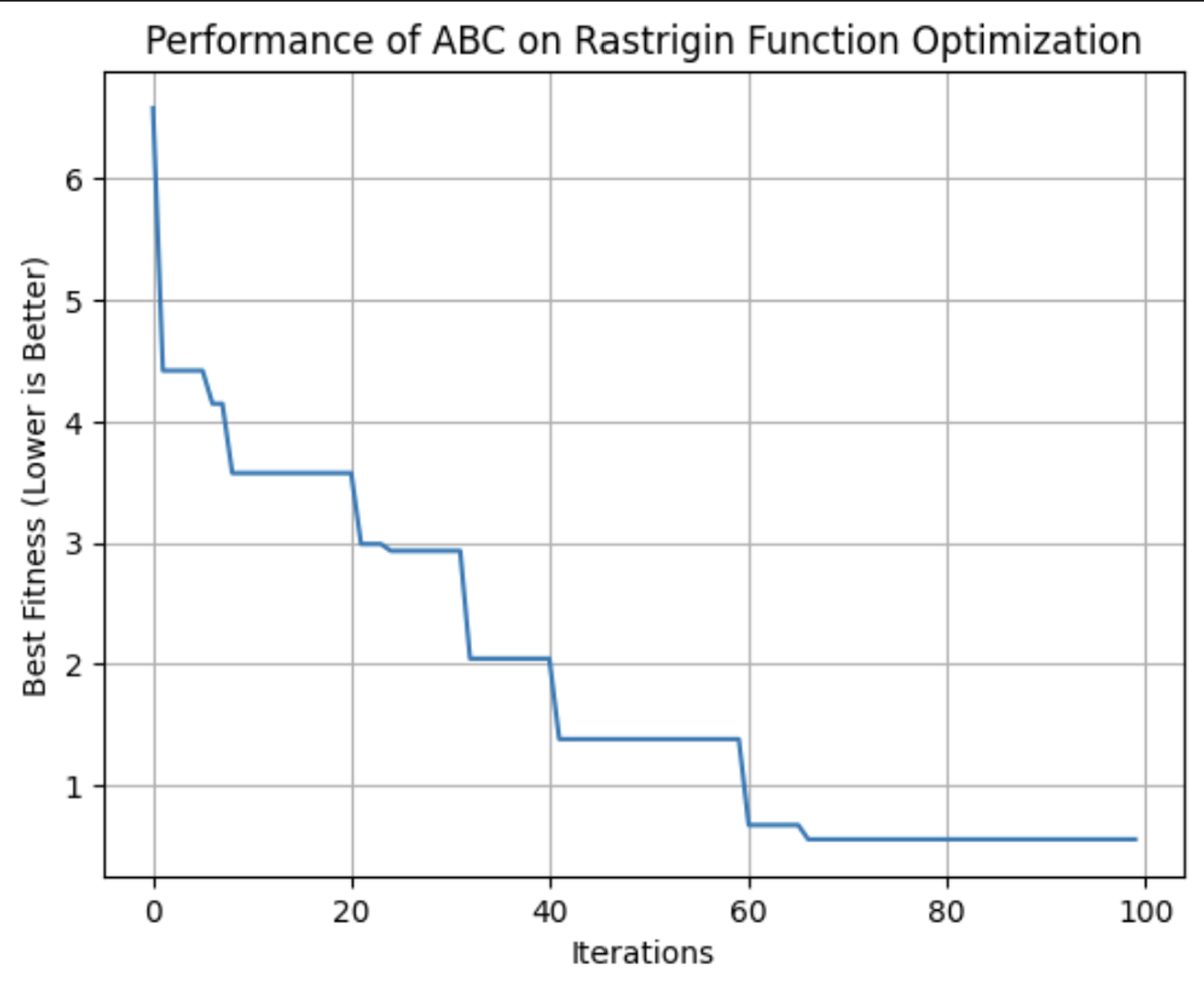
Ce graphique montre l'aptitude de la meilleure solution trouvée par l'algorithme ABC à chaque itération. Lors de cette exécution, il a atteint sa forme optimale aux alentours de la 64e itération.
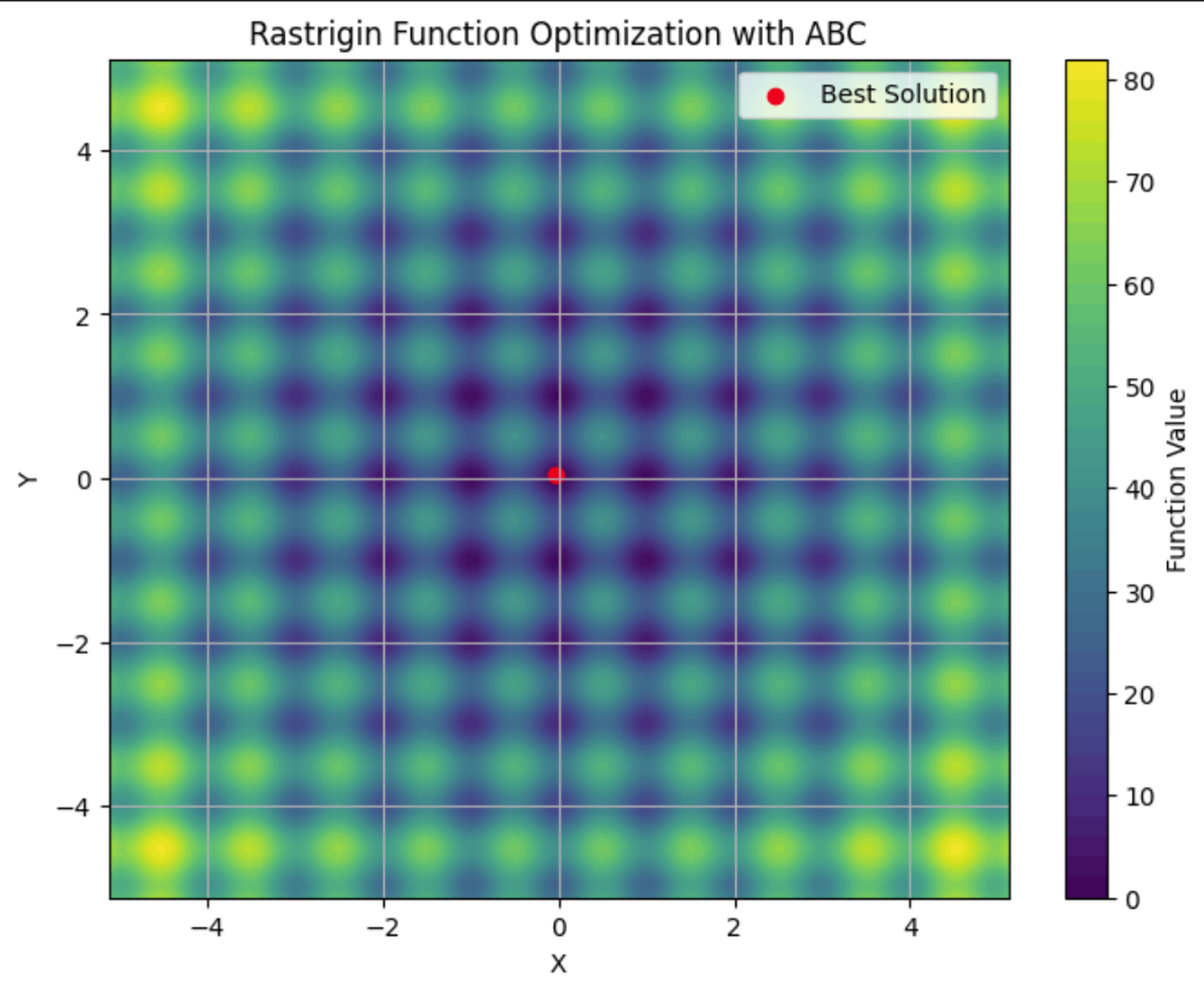
Vous pouvez voir ici la fonction de Rastrigin représentée sur un graphique en courbes de niveau, avec ses nombreux minima locaux. Le point rouge correspond aux minima globaux trouvés par l'algorithme ABC que nous avons exécuté.
Applications des colonies d'abeilles artificielles
L'algorithme ABC est un outil robuste pour résoudre les problèmes d'optimisation. Sa capacité à explorer efficacement des espaces de recherche vastes et complexes en fait un choix de premier ordre pour les secteurs où l'adaptabilité et l'évolutivité sont essentielles.
Ces applications sont les suivantes
- Télécommunications: L'ABC peut être utilisé pour optimiser l'emplacement des ressources du réseau et des antennes, afin de maximiser la couverture et la force du signal tout en minimisant les coûts.
- Ingénierie: L'ABC permet d'affiner les paramètres dans le cadre de l'optimisation de la conception structurelle.
- Science des données: L'ABC peut être appliqué à la sélection des caractéristiques, afin d'identifier les variables les plus importantes d'un ensemble de données pour l'apprentissage automatique.
L'ABC est un algorithme flexible qui convient à tout problème nécessitant la recherche de solutions optimales dans des environnements dynamiques à haute dimension. Sa nature décentralisée le rend bien adapté aux situations dans lesquelles d'autres algorithmes peuvent avoir du mal à équilibrer efficacement l'exploration et l'exploitation.
Comparaison des algorithmes d'intelligence en essaim
Il existe de nombreux algorithmes d'intelligence en essaim, chacun ayant des attributs différents. Au moment de choisir, il est important de peser leurs forces et leurs faiblesses afin de décider lequel répond le mieux à vos besoins.
L'ACO est efficace pour les problèmes combinatoires tels que le routage et l'ordonnancement, mais peut nécessiter des ressources informatiques importantes. PSO est plus simple et excelle dans l'optimisation continue, telle que le réglage des hyperparamètres, mais peut se heurter à des optima locaux. L'ABC réussit à équilibrer l'exploration et l'exploitation, bien qu'il faille l'ajuster avec soin.
D'autres algorithmes d'intelligence en essaim, tels que l'algorithme de la luciole et l'optimisation par recherche de coucouoffrent également des avantages uniques pour des types spécifiques de problèmes d'optimisation .
|
Algorithme |
Points forts |
Faiblesses |
Bibliothèques préférées |
Meilleures applications |
|
Optimisation par colonies de fourmis (ACO) |
Efficace pour les problèmes combinatoires et traite bien les espaces discrets complexes |
Calcul intensif et nécessité d'un réglage fin |
Problèmes d'acheminement, d'ordonnancement et d'affectation des ressources |
|
|
Optimisation par essaims de particules (PSO) |
Bon pour l'optimisation continue et simple à mettre en œuvre |
Peut converger vers des optima locaux et est moins efficace pour les problèmes discrets. |
Réglage des hyperparamètres, conception technique, modélisation financière |
|
|
Colonie d'abeilles artificielle (ABC) |
Adaptation à des problèmes vastes et dynamiques et équilibre entre l'exploration et l'exploitation |
Calcul intensif et nécessité d'un réglage minutieux des paramètres |
Télécommunications, optimisation à grande échelle et espaces de haute dimension |
|
|
Algorithme de la luciole (FA) |
Il excelle dans l'optimisation multimodale et dispose d'une forte capacité de recherche globale. |
Sensible aux paramètres et convergence plus lente |
Traitement d'images, conception technique et optimisation multimodale |
|
|
Recherche de coucous (CS) |
Efficace pour résoudre les problèmes d'optimisation et doté de fortes capacités d'exploration |
Peut converger prématurément et les performances dépendent de la mise au point. |
Ordonnancement, sélection des caractéristiques et applications techniques |
Défis et limites
Les algorithmes d'intelligence en essaim, comme de nombreuses techniques d'apprentissage automatique, rencontrent des difficultés qui peuvent affecter leurs performances. Il s'agit notamment de
- Convergence prématurée: L'essaim peut se fixer trop rapidement sur une solution sous-optimale.
- Réglage des paramètres: Pour obtenir des résultats optimaux, il faut souvent ajuster soigneusement les paramètres de l'algorithme.
- Ressources informatiques et évolutivité: Ces algorithmes peuvent être très gourmands en ressources informatiques, en particulier pour les problèmes complexes et de grande taille, et leurs performances peuvent se dégrader à mesure que la complexité du problème augmente. complexité des problèmes.
- Nature stochastique: Le caractère aléatoire inhérent à ces algorithmes peut entraîner une variabilité des résultats.
Dernières recherches et avancées
Une tendance notable est l'intégration de l'intelligence en essaim avec d'autres techniques d'apprentissage automatique. Les chercheurs étudient comment les algorithmes en essaim peuvent améliorer des tâches telles que la sélection de caractéristiques et l'optimisation des hyperparamètres. Consultez Un algorithme hybride d'optimisation par essaims de particules pour résoudre des problèmes d'ingénierie.
Les avancées récentes s'attachent également à relever certains des défis traditionnels associés à l'intelligence en essaim, tels que la convergence prématurée. De nouveaux algorithmes et de nouvelles techniques sont en cours d'élaboration pour atténuer le risque de convergence vers des solutions sous-optimales. Pour plus d'informations, consultez Approches basées sur la mémoire pour éliminer la convergence prématurée dans l'optimisation par essaims de particules
L'extensibilité est un autre domaine de recherche important. Les problèmes devenant de plus en plus complexes et les volumes de données augmentant, les chercheurs s'efforcent de rendre les algorithmes d'intelligence en essaim plus évolutifs et plus efficaces. Il s'agit notamment de développer des algorithmes capables de traiter plus efficacement les grands ensembles de données et les espaces à haute dimension, tout en optimisant les ressources informatiques afin de réduire le temps et le coût associés à l'exécution de ces algorithmes. Pour en savoir plus, consultez Développements récents dans la théorie et l'applicabilité de la recherche en essaim.
Les algorithmes en essaim sont appliqués à des problèmes allant de la robotiquede la robotique grands modèles de langage (LLM), au diagnostic médical. Des recherche en cours pour savoir si ces algorithmes peuvent être utiles pour aider les LLM à oublier stratégiquement des informations afin de se conformer à la réglementation surle droit à l'oubli. Et, bien sûr, les algorithmes en essaim ont une multitude d'applications dans la science des données. applications dans le domaine de la science des données.
Conclusion
L'intelligence en essaim offre des solutions puissantes aux problèmes d'optimisation dans divers secteurs d'activité. Ses principes de décentralisation, de rétroaction positive et d'adaptation lui permettent de s'attaquer à des tâches complexes et dynamiques que les algorithmes traditionnels pourraient avoir du mal à réaliser.
Consultez cet examen de l'état actuel des algorithmes d'essaimage, "Swarm intelligence : Une étude de la classification des modèles et des applications".
Pour en savoir plus sur les applications commerciales de l'IA, consultez le site suivant Stratégie en matière d'intelligence artificielle (IA) ou Intelligence artificielle pour les dirigeants d'entreprise. Pour en savoir plus sur d'autres algorithmes qui imitent la nature, consultez le site Genetic Algorithm : Guide complet avec implémentation Python.

Je suis titulaire d'un doctorat et j'ai 13 ans d'expérience dans le traitement des données dans un environnement de recherche biologique. Je crée des logiciels dans plusieurs langages de programmation, notamment Python, MATLAB et R. Je suis passionné par le partage de mon amour de l'apprentissage avec le monde.