Track
Imagine watching a flock of birds in flight. There's no leader, no one giving directions, yet they swoop and glide together in perfect harmony. It may look like chaos, but there's a hidden order. You can see the same pattern in schools of fish avoiding predators or ants finding the shortest path to food. These creatures rely on simple rules and local communication to tackle surprisingly complex tasks without central control.
That’s the magic of swarm intelligence.
We can replicate this behavior using algorithms that solve tough problems by mimicking swarm intelligence.
What Is Swarm Intelligence?
Swarm intelligence is a computational approach that solves complex problems by mimicking the decentralized, self-organized behavior observed in natural swarms like flocks of birds or ant colonies.
Let’s explore two key concepts: decentralization and positive feedback.
Decentralization and emergence
At the core of swarm intelligence is the concept of decentralization. Rather than relying on a central leader to direct actions, each individual, or "agent," operates autonomously based on limited, local information.
This decentralized decision-making leads to an emergent property—complex, organized behavior arising from the simple interactions of agents. In swarm systems, the overall outcome, or solution, is not pre-programmed but emerges naturally from these individual actions.
Take ants as an example. When foraging, an ant randomly explores its environment until it finds food, at which point it lays a pheromone trail on its way back to the colony. Other ants encounter this trail and are more likely to follow it, reinforcing the path if they find food at the end. Over time, shorter or more efficient routes naturally attract more ants as stronger pheromone trails build up along these paths. No single ant "knows" the best route from the outset, but collectively, through decentralized decisions and the reinforcement of successful paths, the colony converges on the optimal solution.
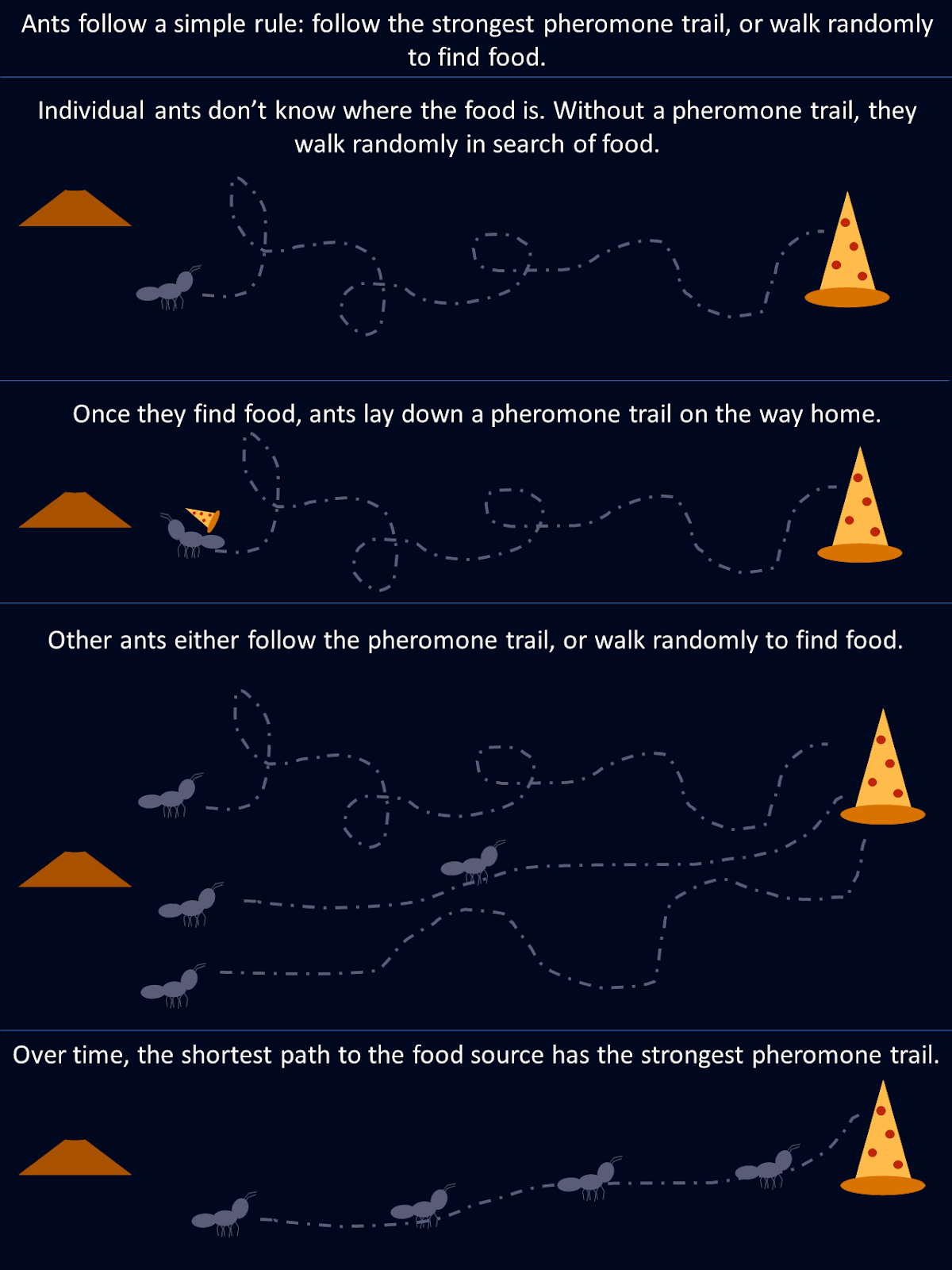
This diagram shows how simple rules followed by individual ants result in an optimal solution for the whole colony.
Positive feedback and adaptation
Positive feedback is a mechanism in swarm intelligence systems, where successful actions are rewarded and reinforced. This leads to a self-amplifying process, like the ants strengthening pheromone trails along shorter foraging paths. This reinforcement of beneficial behaviors helps the swarm improve its overall performance over time.
In artificial intelligence, swarm intelligence algorithms mimic this by adjusting key factors, such as probabilities or weights, based on the quality of the solutions found. As better solutions are discovered, agents increasingly focus on them, which accelerates the convergence process. This dynamic feedback loop allows swarm systems to adapt to changing environments and refine their performance.
There are several swarm intelligence algorithms that mimic different biological systems. Let’s go over a few of the popular ones.
Ant Colony Optimization (ACO)
Ant colony optimization (ACO) is an algorithm inspired by the foraging behavior of ants described above. It’s designed to solve combinatorial optimization problems, particularly those where we need to find the best possible solution among many. A classic example of this is the traveling salesman problem, where the goal is to determine the shortest possible route that connects a set of locations.
How ant colony optimization works
In nature, ants communicate by leaving behind pheromone trails, which signal to other ants the path to a food source. The more ants follow that trail, the stronger it becomes. ACO mimics this behavior with pheromones represented by mathematical values stored in a pheromone matrix. This matrix keeps track of the desirability of different solutions, and it gets updated as the algorithm progresses.
In ACO, each "artificial ant" represents a potential solution to the problem, such as a route in the traveling salesman problem. The algorithm begins with all ants randomly selecting paths, and the pheromone values help guide future ants. These values are stored in a matrix where each entry corresponds to the "pheromone level" between two points (like cities).
- Initialization: The algorithm starts by creating a random set of solutions, with ants exploring different paths.
- Pheromone and heuristic information: Each ant’s path is influenced by two main factors: pheromone levels (how "desirable" a solution is based on previous iterations) and heuristic information (e.g., the distance between two cities). Higher pheromone values make a path more likely to be chosen.
- Updating pheromones: After all ants have completed their paths, the pheromone values are updated. Paths that were part of better solutions get stronger pheromone updates, while those in suboptimal solutions experience evaporation. Mathematically, this is done by increasing the pheromone values in the matrix for good solutions and reducing them over time for others.
- Convergence: Over successive iterations, the pheromone matrix evolves to reflect the best solutions, guiding the ants toward stronger paths. As the process repeats, ants increasingly favor these more successful routes, leading to convergence on the best solution.
This mathematical representation of pheromones allows ACO to effectively balance exploration and exploitation, searching large solution spaces without getting stuck in local optima.
Ant colony optimization Python implementation
Let’s try an example, using ACO to solve a simple problem: find the shortest path between points on a graph.
This implementation of ACO simulates how artificial "ants" traverse 20 nodes on a graph to find the shortest path. Each ant starts at a random node and selects its next move based on pheromone trails and distances between nodes. After exploring all paths, the ants return to their starting point, completing a full loop.
Over time, pheromones are updated: the shorter paths receive stronger reinforcement, while others evaporate. This dynamic process allows the algorithm to converge toward an optimal solution.
import numpy as np
import matplotlib.pyplot as plt
# Graph class represents the environment where ants will travel
class Graph:
def __init__(self, distances):
# Initialize the graph with a distance matrix (distances between nodes)
self.distances = distances
self.num_nodes = len(distances) # Number of nodes (cities)
# Initialize pheromones for each path between nodes (same size as distances)
self.pheromones = np.ones_like(distances, dtype=float) # Start with equal pheromones
# Ant class represents an individual ant that travels across the graph
class Ant:
def __init__(self, graph):
self.graph = graph
# Choose a random starting node for the ant
self.current_node = np.random.randint(graph.num_nodes)
self.path = [self.current_node] # Start path with the initial node
self.total_distance = 0 # Start with zero distance traveled
# Unvisited nodes are all nodes except the starting one
self.unvisited_nodes = set(range(graph.num_nodes)) - {self.current_node}
# Select the next node for the ant to travel to, based on pheromones and distances
def select_next_node(self):
# Initialize an array to store the probability for each node
probabilities = np.zeros(self.graph.num_nodes)
# For each unvisited node, calculate the probability based on pheromones and distances
for node in self.unvisited_nodes:
if self.graph.distances[self.current_node][node] > 0: # Only consider reachable nodes
# The more pheromones and the shorter the distance, the more likely the node will be chosen
probabilities[node] = (self.graph.pheromones[self.current_node][node] ** 2 /
self.graph.distances[self.current_node][node])
probabilities /= probabilities.sum() # Normalize the probabilities to sum to 1
# Choose the next node based on the calculated probabilities
next_node = np.random.choice(range(self.graph.num_nodes), p=probabilities)
return next_node
# Move to the next node and update the ant's path
def move(self):
next_node = self.select_next_node() # Pick the next node
self.path.append(next_node) # Add it to the path
# Add the distance between the current node and the next node to the total distance
self.total_distance += self.graph.distances[self.current_node][next_node]
self.current_node = next_node # Update the current node to the next node
self.unvisited_nodes.remove(next_node) # Mark the next node as visited
# Complete the path by visiting all nodes and returning to the starting node
def complete_path(self):
while self.unvisited_nodes: # While there are still unvisited nodes
self.move() # Keep moving to the next node
# After visiting all nodes, return to the starting node to complete the cycle
self.total_distance += self.graph.distances[self.current_node][self.path[0]]
self.path.append(self.path[0]) # Add the starting node to the end of the path
# ACO (Ant Colony Optimization) class runs the algorithm to find the best path
class ACO:
def __init__(self, graph, num_ants, num_iterations, decay=0.5, alpha=1.0):
self.graph = graph
self.num_ants = num_ants # Number of ants in each iteration
self.num_iterations = num_iterations # Number of iterations
self.decay = decay # Rate at which pheromones evaporate
self.alpha = alpha # Strength of pheromone update
self.best_distance_history = [] # Store the best distance found in each iteration
# Main function to run the ACO algorithm
def run(self):
best_path = None
best_distance = np.inf # Start with a very large number for comparison
# Run the algorithm for the specified number of iterations
for _ in range(self.num_iterations):
ants = [Ant(self.graph) for _ in range(self.num_ants)] # Create a group of ants
for ant in ants:
ant.complete_path() # Let each ant complete its path
# If the current ant's path is shorter than the best one found so far, update the best path
if ant.total_distance < best_distance:
best_path = ant.path
best_distance = ant.total_distance
self.update_pheromones(ants) # Update pheromones based on the ants' paths
self.best_distance_history.append(best_distance) # Save the best distance for each iteration
return best_path, best_distance
# Update the pheromones on the paths after all ants have completed their trips
def update_pheromones(self, ants):
self.graph.pheromones *= self.decay # Reduce pheromones on all paths (evaporation)
# For each ant, increase pheromones on the paths they took, based on how good their path was
for ant in ants:
for i in range(len(ant.path) - 1):
from_node = ant.path[i]
to_node = ant.path[i + 1]
# Update the pheromones inversely proportional to the total distance traveled by the ant
self.graph.pheromones[from_node][to_node] += self.alpha / ant.total_distance
# Generate random distances between nodes (cities) for a 20-node graph
num_nodes = 20
distances = np.random.randint(1, 100, size=(num_nodes, num_nodes)) # Random distances between 1 and 100
np.fill_diagonal(distances, 0) # Distance from a node to itself is 0
graph = Graph(distances) # Create the graph with the random distances
aco = ACO(graph, num_ants=10, num_iterations=30) # Initialize ACO with 10 ants and 30 iterations
best_path, best_distance = aco.run() # Run the ACO algorithm to find the best path
# Print the best path found and the total distance
print(f"Best path: {best_path}")
print(f"Total distance: {best_distance}")
# Plotting the final solution (first plot) - Shows the final path found by the ants
def plot_final_solution(distances, path):
num_nodes = len(distances)
# Generate random coordinates for the nodes to visualize them on a 2D plane
coordinates = np.random.rand(num_nodes, 2) * 10
# Plot the nodes (cities) as red points
plt.scatter(coordinates[:, 0], coordinates[:, 1], color='red')
# Label each node with its index number
for i in range(num_nodes):
plt.text(coordinates[i, 0], coordinates[i, 1], f"{i}", fontsize=10)
# Plot the path (edges) connecting the nodes, showing the best path found
for i in range(len(path) - 1):
start, end = path[i], path[i + 1]
plt.plot([coordinates[start, 0], coordinates[end, 0]],
[coordinates[start, 1], coordinates[end, 1]],
'blue', linewidth=1.5)
plt.title("Final Solution: Best Path")
plt.show()
# Plotting the distance over iterations (second plot) - Shows how the path length improves over time
def plot_distance_over_iterations(best_distance_history):
# Plot the best distance found in each iteration (should decrease over time)
plt.plot(best_distance_history, color='green', linewidth=2)
plt.title("Trip Length Over Iterations")
plt.xlabel("Iteration")
plt.ylabel("Distance")
plt.show()
# Call the plotting functions to display the results
plot_final_solution(distances, best_path)
plot_distance_over_iterations(aco.best_distance_history)![This graph shows the final solution, the best path found, to travel to each node in the shortest distance. In this run, the best route was found to be [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], with a total distance of 129.](https://media.datacamp.com/cms/google/ad_4nxcfk4zmpwq-et7v9dapocc9zbf7nm-mukhnmf83ih4ce-kh30kcuds_7ubqjmnv4ncv_iwr2nzg_oandfg1f6jc_wqkgdpu7jxlp4iilaruergyu4polxvvk5gu8x65jnuckjfj6knyoh-yqf8gpn_inper.png)
This graph shows the final solution, the best path found, to travel to each node in the shortest distance. In this run, the best route was found to be [4, 5, 17, 9, 11, 16, 13, 2, 7, 3, 6, 1, 14, 12, 18, 0, 10, 19, 15, 8, 4], with a total distance of 129.
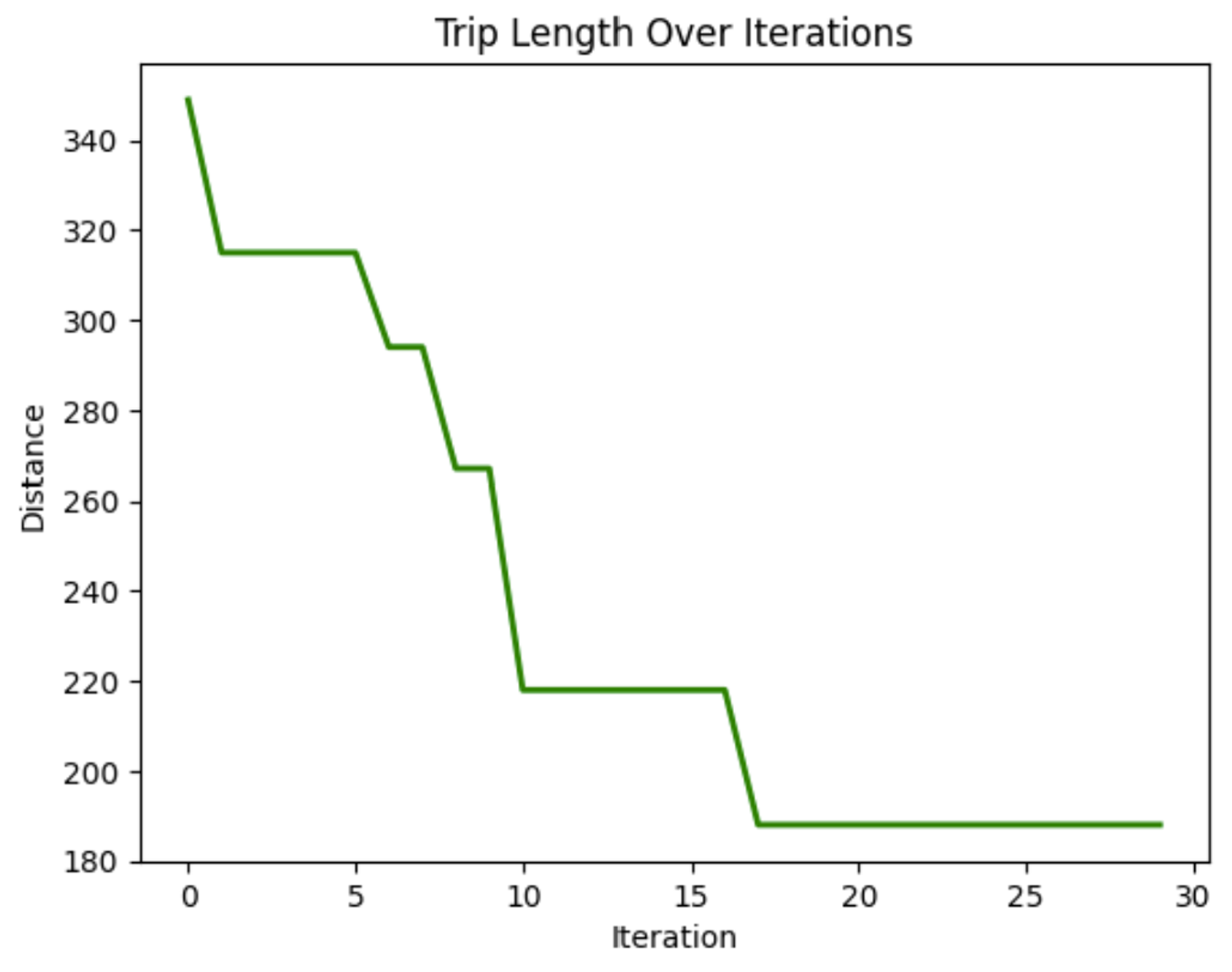
In this graph, we can see the distance traveled while traversing the nodes decreases over iterations. This demonstrates that the model is improving the trip length over time.
Applications of ant colony optimization
ACO’s adaptability and efficiency make it a powerful tool in various industries. Some applications include:
- Routing problems: ACO is used to optimize network routing (e.g., determine the shortest path for data packets in a network), transportation, and delivery services.
- Scheduling: ACO can be applied to scheduling tasks in manufacturing or logistics, ensuring resources are allocated efficiently.
- Resource allocation: The algorithm can be used to allocate limited resources, such as in project management or in complex operations where multiple variables must be considered.
The strength of ACO lies in its ability to evolve and adapt, making it suitable for dynamic environments where conditions can change, such as real-time traffic routing or industrial planning.
Develop AI Applications
Particle Swarm Optimization (PSO)
Particle swarm optimization (PSO) draws its inspiration from the behavior of flocks of birds and schools of fish. In these natural systems, individuals move based on their own previous experiences and their neighbors' positions, gradually adjusting to follow the most successful members of the group. PSO applies this concept to optimization problems, where particles, called agents, move through the search space to find an optimal solution.
Compared to ACO, PSO operates in continuous rather than discrete spaces. In ACO, the focus is on pathfinding and discrete choices, while PSO is better suited for problems involving continuous variables, such as parameter tuning.
In PSO, particles explore a search space. They adjust their positions based on two main factors: their personal best-known position and the best-known position of the entire swarm. This dual feedback mechanism enables them to converge toward the global optimum.
How particle swarm optimization works
The process starts with a swarm of particles initialized randomly across the solution space. Each particle represents a possible solution to the optimization problem. As the particles move, they remember their personal best positions (the best solution they’ve encountered so far) and are attracted toward the global best position (the best solution any particle has found).
This movement is driven by two factors: exploitation and exploration. Exploitation involves refining the search around the current best solution, while exploration encourages particles to search other parts of the solution space to avoid getting stuck in local optima. By balancing these two dynamics, PSO efficiently converges on the best solution.
Particle swarm optimization Python implementation
In financial portfolio management, finding the best way to allocate assets to get the most returns while keeping risks low can be tricky. Let’s use a PSO to find which mix of assets will give us the highest return on investment.
The code below shows how PSO works for optimizing a fictional financial portfolio. It starts with random asset allocations, then tweaks them over several iterations based on what works best, gradually finding the optimal mix of assets for the highest return with the lowest risk.
import numpy as np
import matplotlib.pyplot as plt
# Define the PSO parameters
class Particle:
def __init__(self, n_assets):
# Initialize a particle with random weights and velocities
self.position = np.random.rand(n_assets)
self.position /= np.sum(self.position) # Normalize weights so they sum to 1
self.velocity = np.random.rand(n_assets)
self.best_position = np.copy(self.position)
self.best_score = float('inf') # Start with a very high score
def objective_function(weights, returns, covariance):
"""
Calculate the portfolio's performance.
- weights: Asset weights in the portfolio.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
portfolio_return = np.dot(weights, returns) # Calculate the portfolio return
portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(covariance, weights))) # Calculate portfolio risk (standard deviation)
return -portfolio_return / portfolio_risk # We want to maximize return and minimize risk
def update_particles(particles, global_best_position, returns, covariance, w, c1, c2):
"""
Update the position and velocity of each particle.
- particles: List of particle objects.
- global_best_position: Best position found by all particles.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
- w: Inertia weight to control particle's previous velocity effect.
- c1: Cognitive coefficient to pull particles towards their own best position.
- c2: Social coefficient to pull particles towards the global best position.
"""
for particle in particles:
# Random coefficients for velocity update
r1, r2 = np.random.rand(len(particle.position)), np.random.rand(len(particle.position))
# Update velocity
particle.velocity = (w * particle.velocity +
c1 * r1 * (particle.best_position - particle.position) +
c2 * r2 * (global_best_position - particle.position))
# Update position
particle.position += particle.velocity
particle.position = np.clip(particle.position, 0, 1) # Ensure weights are between 0 and 1
particle.position /= np.sum(particle.position) # Normalize weights to sum to 1
# Evaluate the new position
score = objective_function(particle.position, returns, covariance)
if score < particle.best_score:
# Update the particle's best known position and score
particle.best_position = np.copy(particle.position)
particle.best_score = score
def pso_portfolio_optimization(n_particles, n_iterations, returns, covariance):
"""
Perform Particle Swarm Optimization to find the optimal asset weights.
- n_particles: Number of particles in the swarm.
- n_iterations: Number of iterations for the optimization.
- returns: Expected returns of the assets.
- covariance: Covariance matrix representing risk.
"""
# Initialize particles
particles = [Particle(len(returns)) for _ in range(n_particles)]
# Initialize global best position
global_best_position = np.random.rand(len(returns))
global_best_position /= np.sum(global_best_position)
global_best_score = float('inf')
# PSO parameters
w = 0.5 # Inertia weight: how much particles are influenced by their own direction
c1 = 1.5 # Cognitive coefficient: how well particles learn from their own best solutions
c2 = 0.5 # Social coefficient: how well particles learn from global best solutions
history = [] # To store the best score at each iteration
for _ in range(n_iterations):
update_particles(particles, global_best_position, returns, covariance, w, c1, c2)
for particle in particles:
score = objective_function(particle.position, returns, covariance)
if score < global_best_score:
# Update the global best position and score
global_best_position = np.copy(particle.position)
global_best_score = score
# Store the best score (negative return/risk ratio) for plotting
history.append(-global_best_score)
return global_best_position, history
# Example data for 3 assets
returns = np.array([0.02, 0.28, 0.15]) # Expected returns for each asset
covariance = np.array([[0.1, 0.02, 0.03], # Covariance matrix for asset risks
[0.02, 0.08, 0.04],
[0.03, 0.04, 0.07]])
# Run the PSO algorithm
n_particles = 10 # Number of particles
n_iterations = 10 # Number of iterations
best_weights, optimization_history = pso_portfolio_optimization(n_particles, n_iterations, returns, covariance)
# Plotting the optimization process
plt.figure(figsize=(12, 6))
plt.plot(optimization_history, marker='o')
plt.title('Portfolio Optimization Using PSO')
plt.xlabel('Iteration')
plt.ylabel('Objective Function Value (Negative of Return/Risk Ratio)')
plt.grid(False) # Turn off gridlines
plt.show()
# Display the optimal asset weights
print(f"Optimal Asset Weights: {best_weights}")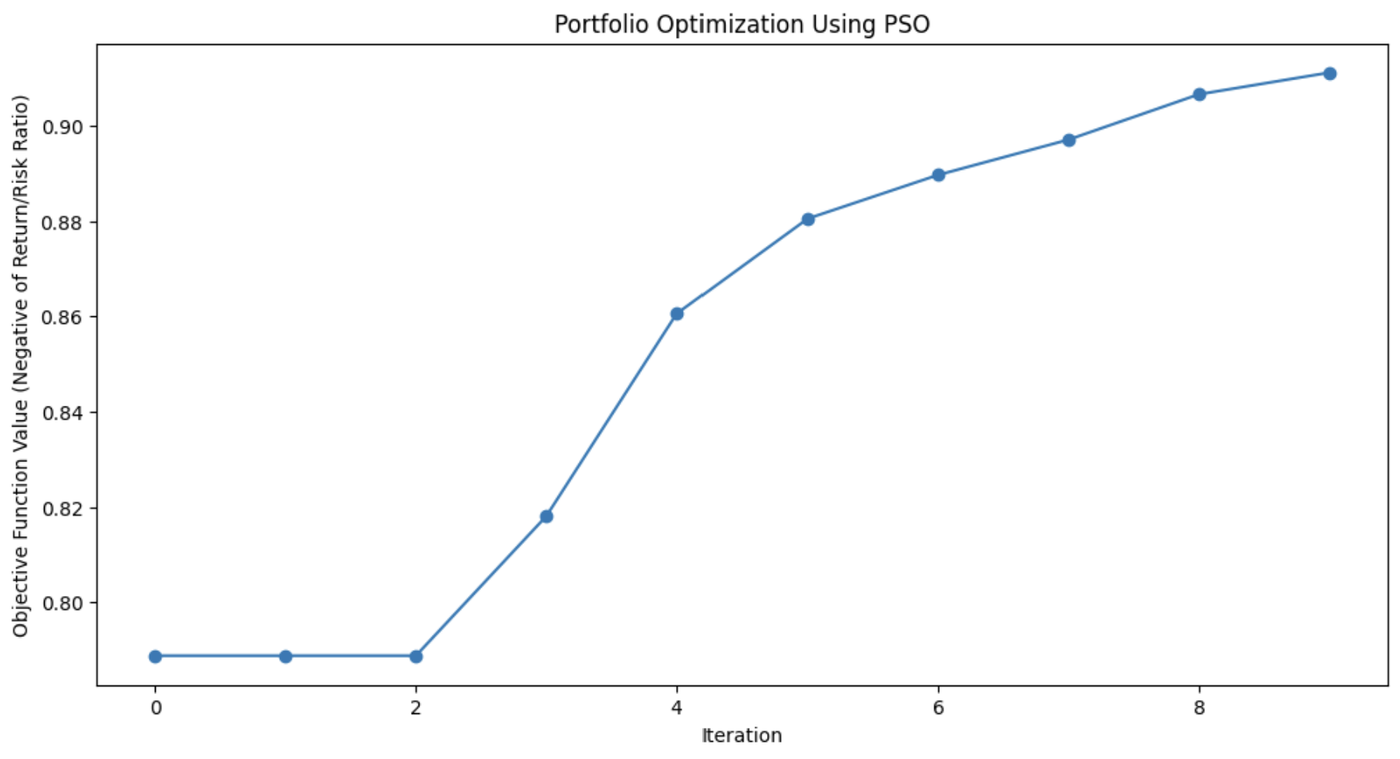
This graph demonstrates how much the PSO algorithm improved the portfolio’s asset mix with each iteration.
Applications of particle swarm optimization
PSO is used for its simplicity and effectiveness in solving various optimization problems, particularly in continuous domains. Its flexibility makes it useful for many real-world scenarios where precise solutions are needed.
These applications include:
- Machine learning: PSO can be applied to tune hyperparameters in machine learning algorithms, helping to find the best model configurations.
- Engineering design: PSO is useful for optimizing design parameters for systems like aerospace components or electrical circuits.
- Financial modeling: In finance, PSO can help in portfolio optimization, minimizing risk while maximizing returns.
PSO's ability to efficiently explore solution spaces makes it applicable across fields, from robotics to energy management to logistics.
Artificial Bee Colony (ABC)
The artificial bee colony (ABC) algorithm is modeled on the foraging behavior of honeybees.
In nature, honeybees efficiently search for nectar sources and share this information with other members of the hive. ABC captures this collaborative search process and applies it to optimization problems, especially those involving complex, high-dimensional spaces.
What sets ABC apart from other swarm intelligence algorithms is its ability to balance exploitation, focusing on refining current solutions, and exploration, searching for new and potentially better solutions. This makes ABC particularly useful for large-scale problems where global optimization is key.
How artificial bee colony works
In the ABC algorithm, the swarm of bees is divided into three specialized roles: employed bees, onlookers, and scouts. Each of these roles mimics a different aspect of how bees search for and exploit food sources in nature.
- Employed bees: These bees are responsible for exploring known food sources, representing current solutions in the optimization problem. They assess the quality (fitness) of these sources and share the information with the rest of the hive.
- Onlooker bees: After gathering information from the employed bees, onlookers select which food sources to explore further. They base their choices on the quality of the solutions shared by the employed bees, focusing more on the better options, thus refining the search for an optimal solution.
- Scout bees: When an employed bee’s food source (solution) becomes exhausted or stagnant (when no improvement is found after a certain number of iterations), the bee becomes a scout. Scouts explore new areas of the solution space, searching for potentially unexplored food sources, thus injecting diversity into the search process.
This dynamic allows ABC to balance the search between intensively exploring promising areas and broadly exploring new areas of the search space. This helps the algorithm avoid getting trapped in local optima and increases its chances of finding a global optimum.
Artificial bee colony Python implementation
The Rastrigin function is a popular problem in optimization, known for its numerous local minima, making it a tough challenge for many algorithms. The goal is simple: find the global minimum.
In this example, we’ll use the artificial bee colony algorithm to tackle this problem. Each bee in the ABC algorithm explores the search space, looking for better solutions to minimize the function. The code simulates bees that explore, exploit, and scout for new areas, ensuring a balance between exploration and exploitation.
import numpy as np
import matplotlib.pyplot as plt
# Rastrigin function: The objective is to minimize this function
def rastrigin(X):
A = 10
return A * len(X) + sum([(x ** 2 - A * np.cos(2 * np.pi * x)) for x in X])
# Artificial Bee Colony (ABC) algorithm for continuous optimization of Rastrigin function
def artificial_bee_colony_rastrigin(n_iter=100, n_bees=30, dim=2, bound=(-5.12, 5.12)):
"""
Apply Artificial Bee Colony (ABC) algorithm to minimize the Rastrigin function.
Parameters:
n_iter (int): Number of iterations
n_bees (int): Number of bees in the population
dim (int): Number of dimensions (variables)
bound (tuple): Bounds for the search space (min, max)
Returns:
tuple: Best solution found, best fitness value, and list of best fitness values per iteration
"""
# Initialize the bee population with random solutions within the given bounds
bees = np.random.uniform(bound[0], bound[1], (n_bees, dim))
best_bee = bees[0]
best_fitness = rastrigin(best_bee)
best_fitnesses = []
for iteration in range(n_iter):
# Employed bees phase: Explore new solutions based on the current bees
for i in range(n_bees):
# Generate a new candidate solution by perturbing the current bee's position
new_bee = bees[i] + np.random.uniform(-1, 1, dim)
new_bee = np.clip(new_bee, bound[0], bound[1]) # Keep within bounds
# Evaluate the fitness of the new solution
new_fitness = rastrigin(new_bee)
if new_fitness < rastrigin(bees[i]):
bees[i] = new_bee # Update bee if the new solution is better
# Onlooker bees phase: Exploit good solutions
fitnesses = np.array([rastrigin(bee) for bee in bees])
probabilities = 1 / (1 + fitnesses) # Higher fitness gets higher chance
probabilities /= probabilities.sum() # Normalize probabilities
for i in range(n_bees):
if np.random.rand() < probabilities[i]:
selected_bee = bees[i]
# Generate a new candidate solution by perturbing the selected bee
new_bee = selected_bee + np.random.uniform(-0.5, 0.5, dim)
new_bee = np.clip(new_bee, bound[0], bound[1])
if rastrigin(new_bee) < rastrigin(selected_bee):
bees[i] = new_bee
# Scouting phase: Randomly reinitialize some bees to explore new areas
if np.random.rand() < 0.1: # 10% chance to reinitialize a bee
scout_index = np.random.randint(n_bees)
bees[scout_index] = np.random.uniform(bound[0], bound[1], dim)
# Track the best solution found so far
current_best_bee = bees[np.argmin(fitnesses)]
current_best_fitness = min(fitnesses)
if current_best_fitness < best_fitness:
best_fitness = current_best_fitness
best_bee = current_best_bee
best_fitnesses.append(best_fitness)
return best_bee, best_fitness, best_fitnesses
# Apply ABC to minimize the Rastrigin function
best_solution, best_fitness, best_fitnesses = artificial_bee_colony_rastrigin()
# Display results
print("Best Solution (x, y):", best_solution)
print("Best Fitness (Minimum Value):", best_fitness)
# Plot the performance over iterations
plt.figure()
plt.plot(best_fitnesses)
plt.title('Performance of ABC on Rastrigin Function Optimization')
plt.xlabel('Iterations')
plt.ylabel('Best Fitness (Lower is Better)')
plt.grid(True)
plt.show()
# Plot a surface graph of the Rastrigin function
x = np.linspace(-5.12, 5.12, 200)
y = np.linspace(-5.12, 5.12, 200)
X, Y = np.meshgrid(x, y)
Z = 10 * 2 + (X ** 2 - 10 * np.cos(2 * np.pi * X)) + (Y ** 2 - 10 * np.cos(2 * np.pi * Y))
plt.figure(figsize=(8, 6))
plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.colorbar(label='Function Value')
plt.scatter(best_solution[0], best_solution[1], c='red', label='Best Solution')
plt.title('Rastrigin Function Optimization with ABC')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()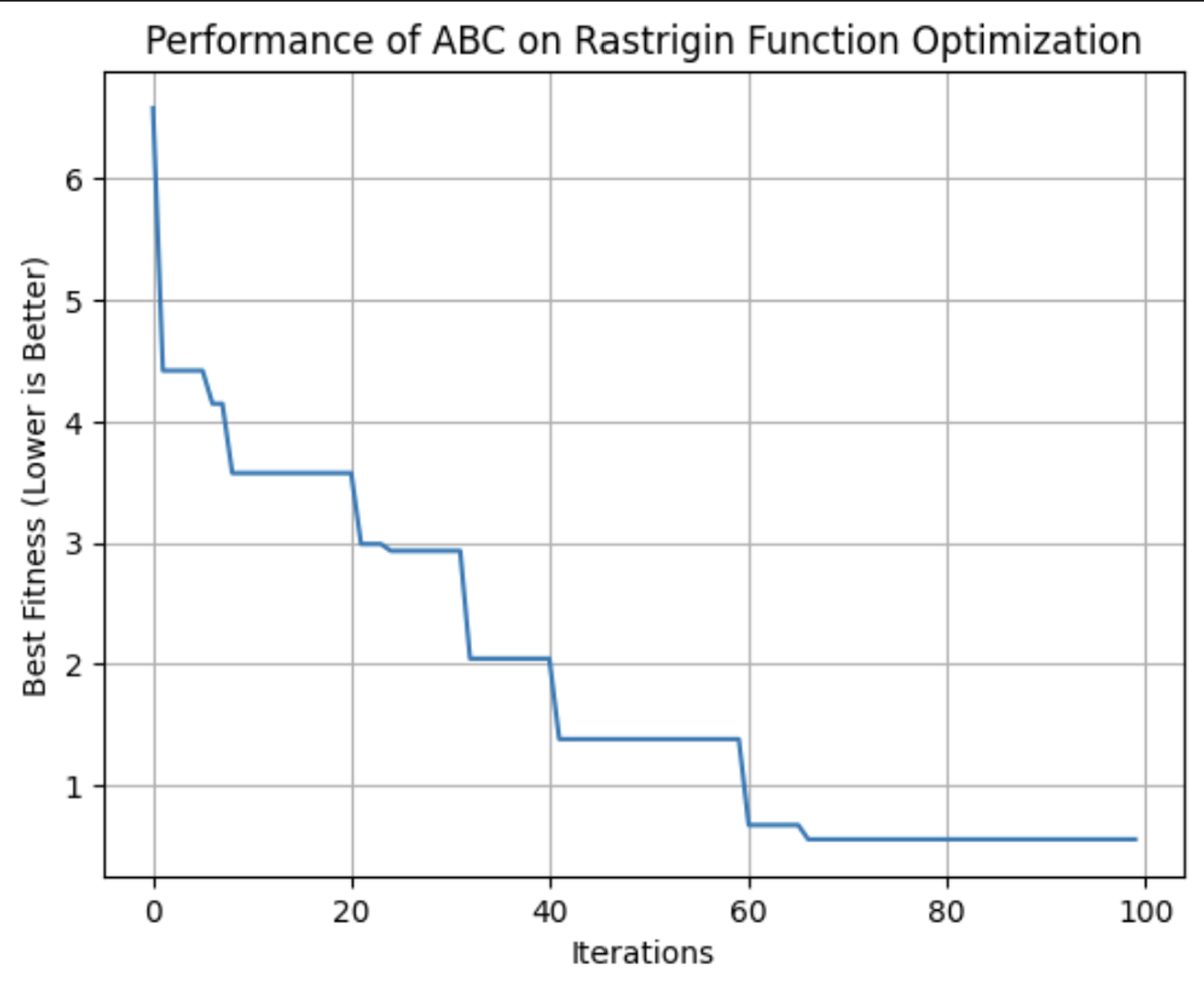
This graph shows the fitness of the best solution found by the ABC algorithm with each iteration. In this run, it reached its optimum fitness around the 64th iteration.
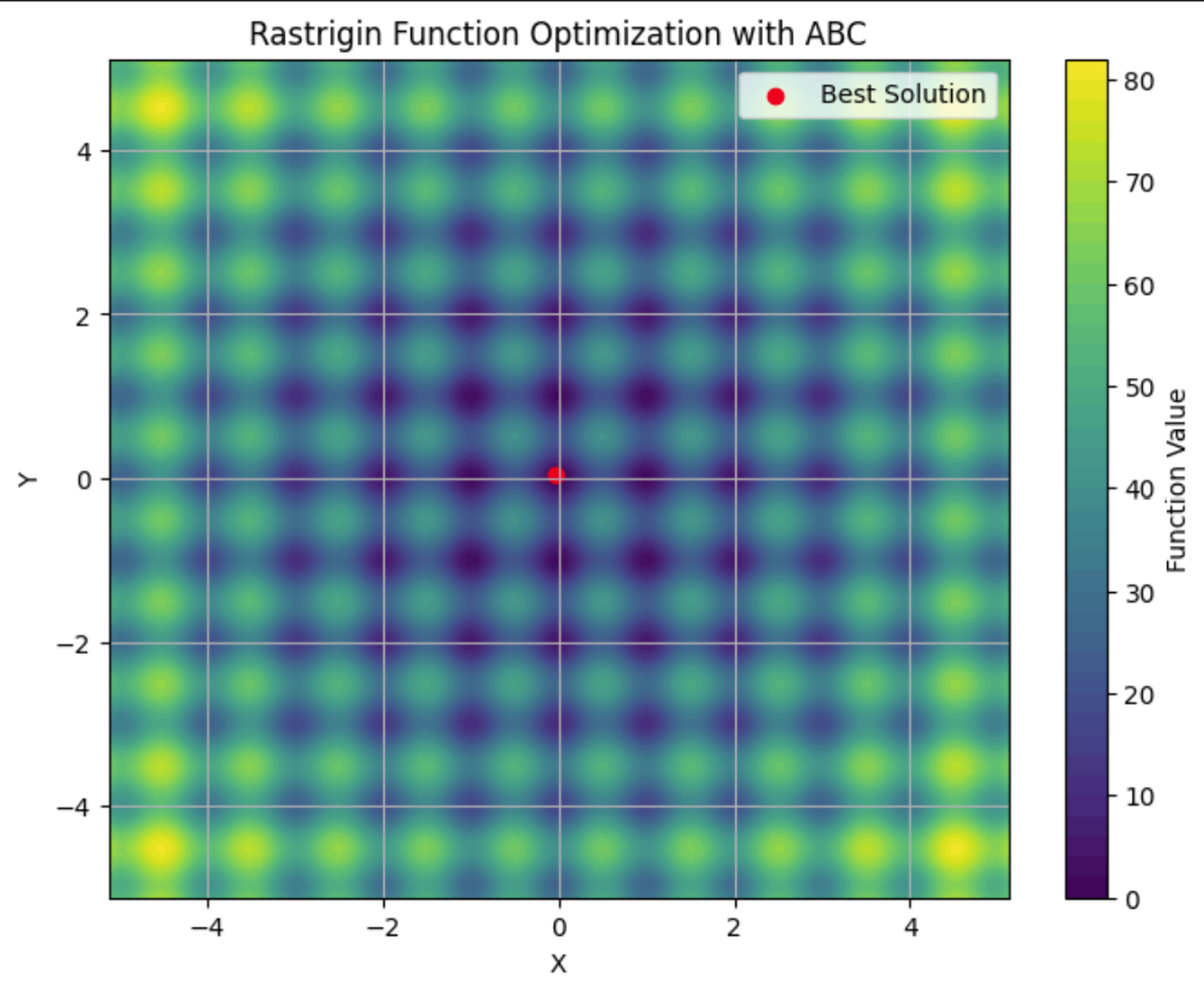
Here you can see the Rastrigin function plotted on a contour plot, with its many local minima. The red dot is the global minima found by the ABC algorithm we ran.
Applications of artificial bee colony
The ABC algorithm is a robust tool for solving optimization problems. Its ability to efficiently explore large and complex search spaces makes it a go-to choice for industries where adaptability and scalability are critical.
These applications include:
- Telecommunications: ABC can be used to optimize the placement of network resources and antennas, maximizing coverage and signal strength while minimizing costs.
- Engineering: ABC can fine-tune parameters in structural design optimization.
- Data Science: ABC can be applied to feature selection, to identify the most important variables in a dataset for machine learning.
ABC is a flexible algorithm suitable for any problem where optimal solutions need to be found in dynamic, high-dimensional environments. Its decentralized nature makes it well-suited for situations where other algorithms may struggle to balance exploration and exploitation efficiently.
Comparing Swarm Intelligence Algorithms
There are multiple swarm intelligence algorithms, each with different attributes. When deciding which to use, it's important to weigh their strengths and weaknesses to decide which best suits your needs.
ACO is effective for combinatorial problems like routing and scheduling but may need significant computational resources. PSO is simpler and excels in continuous optimization, such as hyperparameter tuning, but can struggle with local optima. ABC successfully balances exploration and exploitation, though it requires careful tuning.
Other swarm intelligence algorithms, such as Firefly Algorithm and Cuckoo Search Optimization, also offer unique advantages for specific types of optimization problems.
|
Algorithm |
Strengths |
Weaknesses |
Preferred Libraries |
Best Applications |
|
Ant Colony Optimization (ACO) |
Effective for combinatorial problems and handles complex discrete spaces well |
Computationally intensive and requires fine-tuning |
Routing problems, scheduling, and resource allocation |
|
|
Particle Swarm Optimization (PSO) |
Good for continuous optimization and simple and easy to implement |
Can converge to local optima and is less effective for discrete problems |
Hyperparameter tuning, engineering design, financial modeling |
|
|
Artificial Bee Colony (ABC) |
Adaptable to large, dynamic problems and balanced exploration and exploitation |
Computationally intensive and requires careful parameter tuning |
Telecommunications, large-scale optimization, and high-dimensional spaces |
|
|
Firefly Algorithm (FA) |
Excels in multimodal optimization and has strong global search ability |
Sensitive to parameter settings and slower convergence |
Image processing, engineering design, and multimodal optimization |
|
|
Cuckoo Search (CS) |
Efficient for solving optimization problems and has strong exploration capabilities |
May converge prematurely and performance depends on tuning |
Scheduling, feature selection, and engineering applications |
Challenges and Limitations
Swarm intelligence algorithms, like many machine learning techniques, encounter challenges that can affect their performance. These include:
- Premature convergence: The swarm may settle on a suboptimal solution too quickly.
- Parameter tuning: Achieving optimal results often requires careful adjustment of algorithm settings.
- Computational resources & scalability: These algorithms can be computationally intensive, especially with larger, more complex problems, and their performance might degrade as problem complexity increases.
- Stochastic nature: The inherent randomness in these algorithms can lead to variability in results.
Latest Research and Advancements
A notable trend is the integration of swarm intelligence with other machine learning techniques. Researchers are exploring how swarm algorithms can enhance tasks such as feature selection and hyperparameter optimization. Check out A hybrid particle swarm optimization algorithm for solving engineering problem.
Recent advancements also focus on addressing some of the traditional challenges associated with swarm intelligence, such as premature convergence. New algorithms and techniques are being developed to mitigate the risk of converging on suboptimal solutions. For more information, check out Memory-based approaches for eliminating premature convergence in particle swarm optimization
Scalability is another significant area of research. As problems become increasingly complex and data volumes grow, researchers are working on ways to make swarm intelligence algorithms more scalable and efficient. This includes developing algorithms that can handle large datasets and high-dimensional spaces more effectively, while optimizing computational resources to reduce the time and cost associated with running these algorithms. For more on this, check out Recent Developments in the Theory and Applicability of Swarm Search.
Swarm algorithms are being applied to problems from robotics, to large language models (LLMs), to medical diagnosis. There is ongoing research into whether these algorithms can be useful for helping LLMs strategically forget information to comply with Right to Be Forgotten regulations. And, of course, swarm algorithms have a multitude of applications in data science.
Conclusion
Swarm intelligence offers powerful solutions for optimization problems across various industries. Its principles of decentralization, positive feedback, and adaptation allow it to tackle complex, dynamic tasks that traditional algorithms might struggle with.
Check out this review of the current state of swarm algorithms, “Swarm intelligence: A survey of model classification and applications”.
For a deeper dive into the business applications of AI, check out Artificial Intelligence (AI) Strategy or Artificial Intelligence for Business Leaders. To learn about other algorithms that imitate nature, check out Genetic Algorithm: Complete Guide With Python Implementation.

I am a PhD with 13 years of experience working with data in a biological research environment. I create software in several programming languages including Python, MATLAB, and R. I am passionate about sharing my love of learning with the world.
