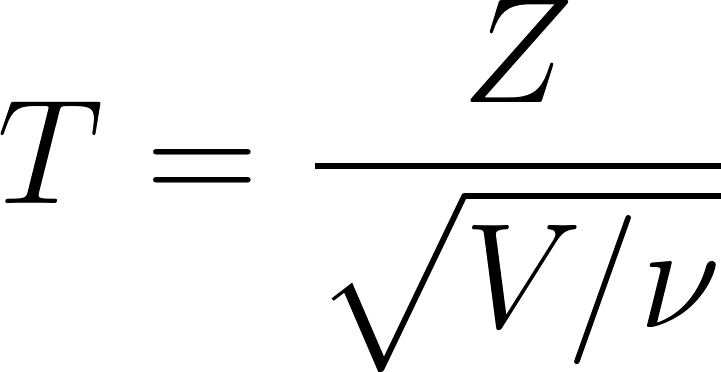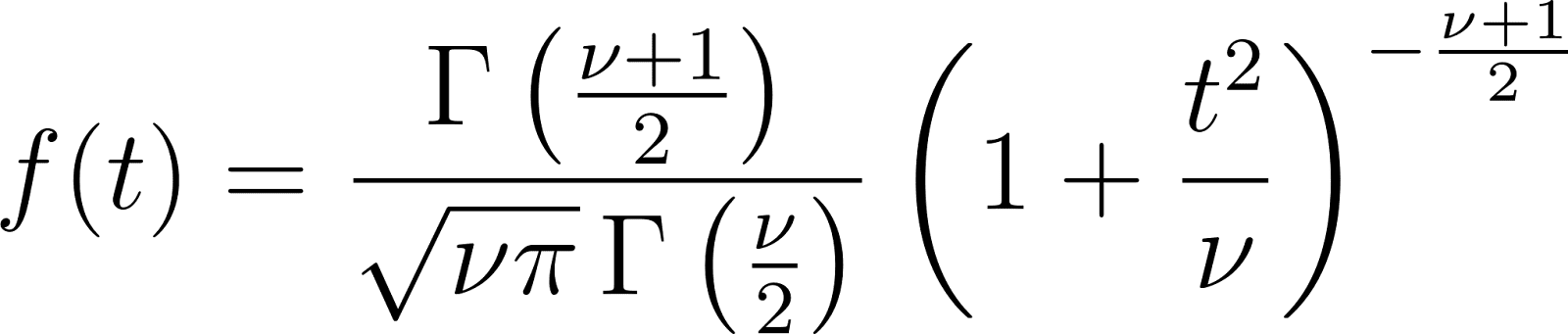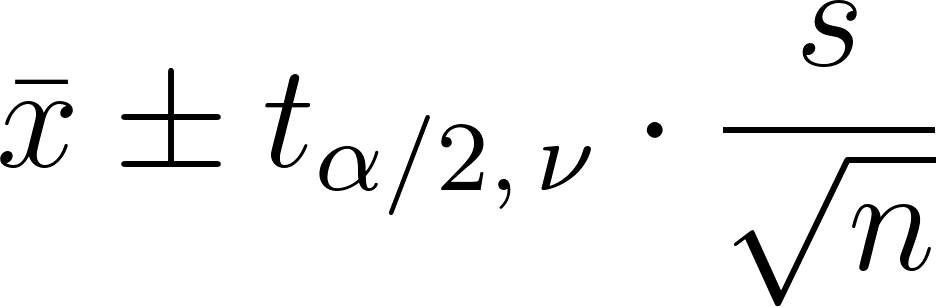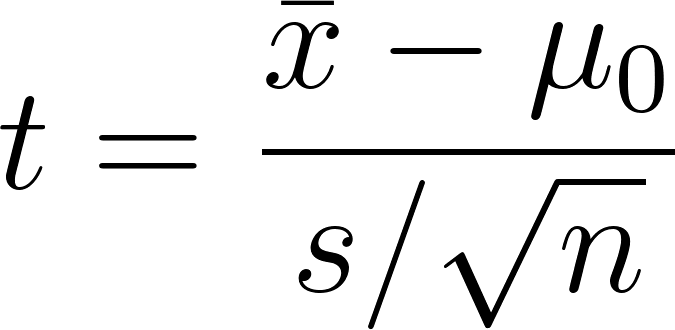Cuando se trabaja con datos del mundo real, suele ocurrir que el tamaño de las muestras sea pequeño o que se desconozca la varianza de la población. Éstas son las condiciones en las que las técnicas estadísticas tradicionales basadas en la distribución normal pueden no ser válidas. Ahí es donde resulta útil la distribución t, también conocida como distribución t de Student. Es una herramienta poderosa para hacer inferencias estadísticas fiables cuando los datos son limitados o la incertidumbre es alta.
En este artículo estudiaremos qué es la distribución t, cómo se compara con otras distribuciones similares, sus propiedades matemáticas clave y cómo se utiliza en la práctica, sobre todo en las pruebas de hipótesis y los intervalos de confianza. También he incluido una tabla de distribución t al final para una referencia rápida.
¿Qué es la distribución T?
Al igual que la distribución normal, la distribución t también es simétrica y tiene forma de campana. Sin embargo, tiene colas más pesadas que reflejan la mayor incertidumbre que suele acompañar a las muestras de menor tamaño.
Además, hay otro factor clave que diferencia a la distribución t: se define por sus grados de libertad (df). Este valor, df, se calcula como el tamaño de la muestra menos uno (n - 1) e influye en la forma de la distribución.
A medida que aumentan los grados de libertad, la distribución t se parece más a la distribución normal. Cuando el tamaño de la muestra es grande (por ejemplo, n > 30), la diferencia llega a ser tan pequeña que la distribución t empieza a parecerse a la curva normal estándar.
Distribución T vs. Otras distribuciones similares
Es útil comparar la distribución t con otras similares.
Distribución T vs. distribución normal
Aunque hemos observado que ambas distribuciones tienen forma de campana, la distribución t tiene colas más gruesas y es más adecuada para muestras pequeñas y varianza poblacional desconocida, es especialmente importante destacar su tolerancia a los valores atípicos.
|
Función |
distribución t |
Distribución normal |
|
Forma |
Colas acampanadas y más pesadas |
Cola acampanada y más fina |
|
Caso práctico |
Muestras pequeñas, σ desconocida |
Muestras grandes, σ conocidas |
|
Grados de libertad |
Necesario |
No aplicable |
|
Sensibilidad a los valores atípicos |
Más tolerante |
Menos tolerante |
Para muestras más grandes, el teorema del límite central justifica el uso de la distribución normal, ya que las medias muestrales tienden a seguir una distribución normal independientemente de la forma de la población.
Distribución T vs. Z-distribution
La distribución Z se refiere a la distribución normal estándar, que tiene una media de 0 y una desviación estándar de 1.
|
Función |
distribución t |
Distribución Z |
|
¿Varianza conocida? |
No |
Sí |
|
Espesor de la cola |
Más pesado |
Más fino |
|
Prueba común |
Pruebas T |
Pruebas Z |
|
Uso para muestras pequeñas |
Sí |
No |
Vamos a entenderlo con un ejemplo de código Python:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm
# X-axis range
x = np.linspace(-5, 5, 1000)
# Standard Normal (Z) Distribution
z_dist = norm.pdf(x)
# Plotting
plt.figure(figsize=(10, 6))
plt.plot(x, z_dist, label='Z-Distribution (Standard Normal)', color='black', linewidth=2)
# T-Distributions with different degrees of freedom
dfs = [1, 3, 5, 10, 30]
colors = ['red', 'orange', 'green', 'blue', 'purple']
for df, color in zip(dfs, colors):
t_dist = t.pdf(x, df)
plt.plot(x, t_dist, label=f'T-Distribution (df={df})', color=color, linestyle='--')
plt.title('T-Distribution vs Z-Distribution: Heavier Tails for Smaller Sample Sizes')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()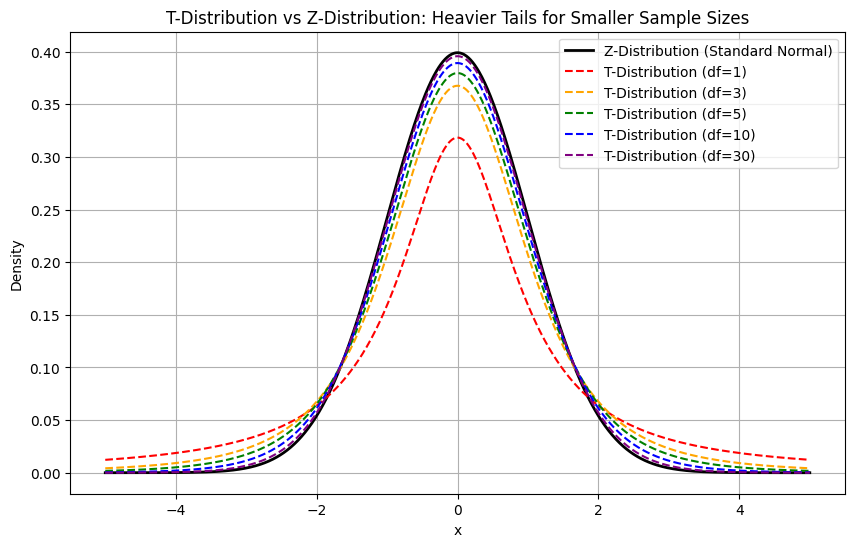
Casos especiales y distribuciones relacionadas
La distribución t está estrechamente relacionada con otras distribuciones de probabilidad:
- Distribución normal estándar (como df → ∞): La distribución t converge a la distribución normal a medida que aumentan los grados de libertad.
- Distribución de Cauchy (df = 1): Una distribución t con 1 grado de libertad es equivalente a la distribución de Cauchy, conocida por tener una media y una varianza indefinidas, lo que significa que, en la práctica, una distribución t con 1 grado de libertad se utiliza muy poco.
- Distribución F: El cuadrado de una variable con distribución t con ν grados de libertad sigue una distribución F con (1, ν) grados de libertad.
- Distribución t no central: Utilizada en análisis de potencia y aplicaciones estadísticas avanzadas, esta versión incorpora un parámetro de no centralidad, que surge cuando la hipótesis nula es falsa.
Limitaciones de la distribución T
La distribución t supone que los datos subyacentes tienen una distribución aproximadamente normal. En casos de datos muy sesgados o no normales, puede no ser adecuado. Las técnicas estadísticas robustas o los métodos no paramétricos pueden ser más adecuados en estos casos.
Ahora comparemos cómo se comporta la prueba t con datos normales frente a datos asimétricos, teniendo ambos la misma media.
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
np.random.seed(42)
# Generate data
normal_data = np.random.normal(loc=0, scale=1, size=30)
skewed_data = np.random.exponential(scale=1.0, size=30) - 1 # Shift to mean ≈ 0
# Perform one-sample t-tests (test if mean == 0)
t_stat_normal, p_normal = stats.ttest_1samp(normal_data, popmean=0)
t_stat_skewed, p_skewed = stats.ttest_1samp(skewed_data, popmean=0)
# Plot histograms
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(normal_data, bins=15, color='skyblue', edgecolor='black')
plt.title(f'Normal Data\np-value = {p_normal:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.subplot(1, 2, 2)
plt.hist(skewed_data, bins=15, color='salmon', edgecolor='black')
plt.title(f'Skewed Data\np-value = {p_skewed:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.suptitle("Impact of Data Shape on t-test")
plt.tight_layout()
plt.show()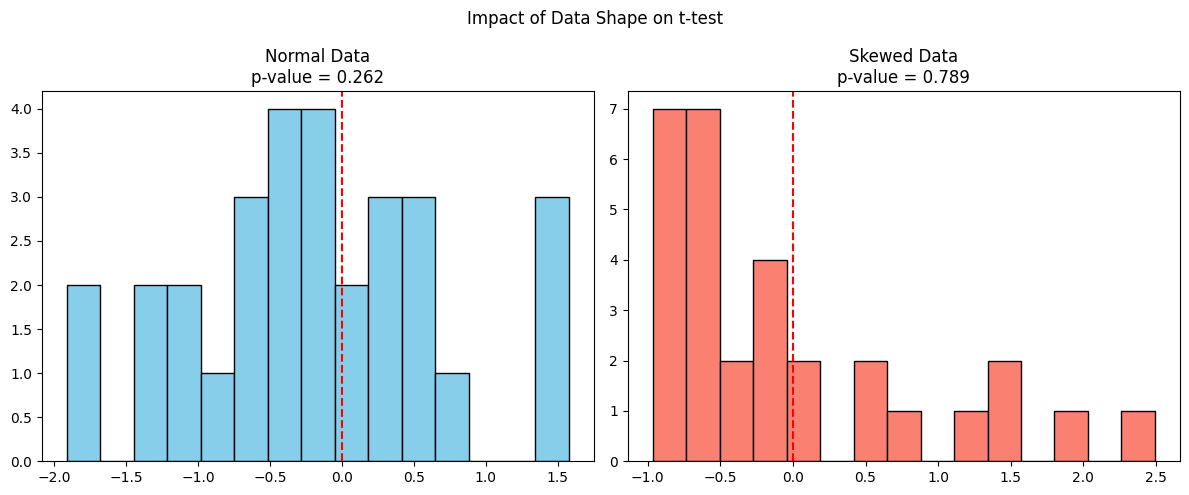
El gráfico de la izquierda muestra datos de una distribución normal en la que la prueba t es válida, y el valor p es fiable. Mientras que el gráfico de la derecha muestra datos asimétricos de una distribución exponencial, aunque la media muestral sea similar, la prueba t asume la simetría y no tiene en cuenta la asimetría, lo que puede dar un valor p inexacto.
Propiedades matemáticas de la distribución T
La distribución t se define como:
Dónde:
- T es el valor resultante que sigue una distribución t de Student con ν grados de libertad
- Z es una variable aleatoria normal estándar Z∼N(0,1)
- V es una variable aleatoria de distribución chi-cuadrado con ν grados de libertad, V∼χ2(ν)
- v es el parámetro de grados de libertad, a menudo igual a n-1, donde n es el tamaño de la muestra.
Función de densidad de probabilidad (PDF)
Propiedades clave
- Media: 0 (para v > 1 )
- Varianza: v /(v - 2) (para v > 2)
- Asimetría: 0 (distribución simétrica)
- Kurtosis: Distribución superior a la normal (leptocúrtica)
Simulación
Los métodos de Montecarlo se utilizan con frecuencia para simular variables aleatorias con distribución t, especialmente cuando se evalúa la significación estadística o se crean datos sintéticos.
Vamos a simularlo utilizando Python.
Aquí, nuestro objetivo es simular un gran número de experimentos con muestras pequeñas (tamaño de la muestra = 10), calcular el estadístico t de cada uno y comparar la distribución resultante con la distribución t teórica.
Para ello, debemos seguir el planteamiento siguiente:
- Genera muchas muestras a partir de una distribución normal (media = 0, std = 1).
- Para cada muestra, calcula el estadístico t: (Resta la media de la población μ de la media muestral xˉy divide el resultado por el error típico de la media, que es la desviación estándar de la muestra s dividida por la raíz cuadrada del tamaño de la muestra n)
- Graficando el histograma de los valores t simulados.
- Superpón la distribución t teórica para comparar.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t
# Simulation parameters
n = 10 # sample size
mu = 0 # population mean
sigma = 1 # population std deviation (not used directly)
df = n - 1 # degrees of freedom
num_simulations = 10000 # number of Monte Carlo simulations
# Monte Carlo simulation
t_stats = []
for _ in range(num_simulations):
sample = np.random.normal(loc=mu, scale=sigma, size=n)
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1) # sample std dev with Bessel's correction
t_stat = (sample_mean - mu) / (sample_std / np.sqrt(n))
t_stats.append(t_stat)
# Plot histogram of simulated t-statistics
x = np.linspace(-5, 5, 1000)
plt.figure(figsize=(10, 6))
plt.hist(t_stats, bins=50, density=True, alpha=0.6, label='Simulated t-Statistics')
# Overlay theoretical t-distribution
plt.plot(x, t.pdf(x, df), label=f'Theoretical t-Distribution (df={df})', color='red', linewidth=2)
plt.title('Monte Carlo Simulation of t-Distribution (n=10)')
plt.xlabel('t-value')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()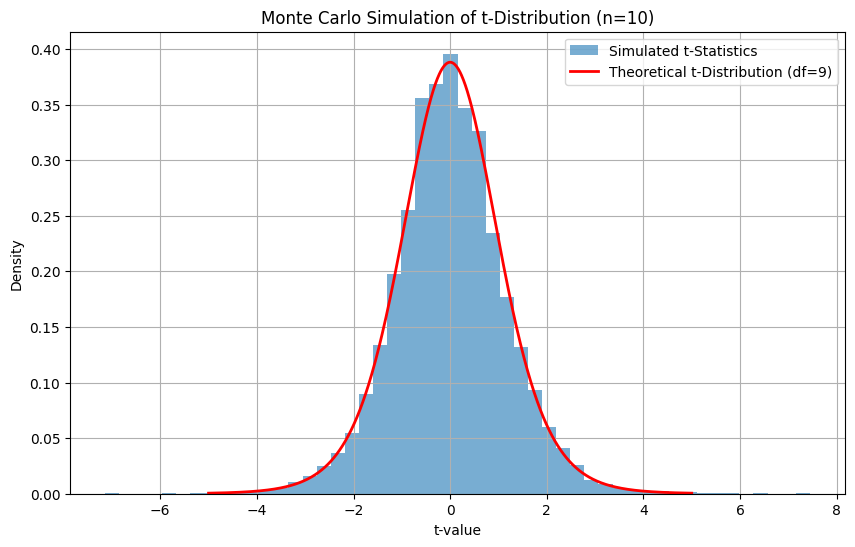
Los valores t simulados forman una distribución que se aproxima mucho a la distribución t teórica con df = 9. Se trata de una forma práctica de comprender y validar la distribución t mediante un muestreo aleatorio. También es un concepto fundamental detrás del bootstrapping y de la inferencia basada en el remuestreo.
Cuándo utilizar la distribución T
La distribución t es fundamental en muchas aplicaciones estadísticas:
- Estimación de medias poblacionales cuando se desconoce la desviación estándar
- Comprobación de hipótesis mediante pruebas t
- Intervalos de confianza para muestras pequeñas
- Análisis de regresión, donde los coeficientes siguen una distribución t
- La inferencia bayesiana, especialmente cuando los parámetros de varianza están marginados
Intervalos de confianza con la distribución t
Un intervalo de confianza para la media se calcula como:
Dónde:
- x es la media muestral
- s es la desviación estándar de la muestra
- n es el tamaño de la muestra
- Y la parte central es el valor crítico de la distribución t.(alfa es el nivel de significación, y alfa dividido por dos es porque es de dos colas).
Utiliza una tabla de distribución t o una calculadora para hallar el valor crítico.
Comprobación de hipótesis con la distribución t
En las pruebas t, el estadístico de la prueba es:
Lo comparas con un valor t crítico para aceptar o rechazar la hipótesis nula. Las pruebas T pueden ser:
- Una muestra
- Dos muestras
- Muestra pareada
Las ilustraciones gráficas ayudan a visualizar las regiones críticas en las pruebas de una y dos colas.
Tabla de distribución T
Una tabla de distribución t enumera los valores críticos de la distribución t para distintos niveles de confianza y grados de libertad. Es esencial para:
- Determinar los intervalos de confianza
- Realización de pruebas t
- Comprobación de la significación en la regresión
Si te resulta útil, he incluido una versión resumida de una tabla de distribución t que puedes consultar aquí:
| df | 80% (1 cola) | 90% (2 colas) | 95% (2 colas) | 98% (2 colas) | 99% (2 colas) |
|---|---|---|---|---|---|
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 |
| 30 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 |
| 60 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 |
| ∞ | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 |
Conclusión
Espero que este artículo te haya proporcionado una sólida comprensión de la distribución t y te haya ayudado a salvar la distancia entre la teoría y la práctica. Es un concepto básico de la estadística que trata la incertidumbre, especialmente con muestras de pequeño tamaño o parámetros de población desconocidos.
Además, la distribución t seguirá apareciendo a medida que trabajemos con datos más avanzados, como los que implican estadística robusta y métodos bayesianos. Te recomiendo que te matricules en nuestro programa de Estadístico en R para convertirte realmente en un experto.

Transformadora de Datos y Estratega de IA | Conferenciante Internacional | Ética de la IA | Inventora | Mujer Logradora Global | Autora
Preguntas frecuentes sobre la distribución T
¿Qué es la distribución t y cuándo debe utilizarse?
La distribución t, o distribución t de Student, es una distribución de probabilidad que se utiliza cuando se trabaja con muestras de pequeño tamaño o cuando se desconoce la varianza de la población. Es especialmente útil para comprobar hipótesis y construir intervalos de confianza en estas condiciones.
¿En qué se diferencia la distribución t de la distribución normal (z)?
Aunque ambas tienen forma de campana y son simétricas, la distribución t tiene colas más pesadas, lo que la hace más robusta para muestras pequeñas y datos con posibles valores atípicos. La distribución normal supone una varianza poblacional conocida y es más adecuada para muestras grandes.
¿Qué son los grados de libertad (df) y cómo afectan a la distribución t?
Los grados de libertad, que suelen calcularse como n - 1 para una muestra de tamaño n, determinan la forma de la distribución t. A medida que aumenta df, la distribución t se aproxima a la distribución normal, lo que las hace casi idénticas para muestras grandes.
¿Puede la distribución t manejar datos sesgados o no normales?
La distribución t supone que los datos son aproximadamente normales. Para datos muy sesgados o no normales, su uso puede dar lugar a resultados inexactos. En estos casos, los métodos estadísticos robustos o no paramétricos pueden ser más apropiados.
¿Cuáles son algunas aplicaciones de la distribución t en el mundo real?
Se utiliza habitualmente en las pruebas t (por ejemplo, pruebas t de una muestra, de dos muestras y por parejas) para determinar si las medias difieren significativamente. También se utiliza para construir intervalos de confianza cuando el tamaño de la muestra es pequeño o se desconoce la varianza.