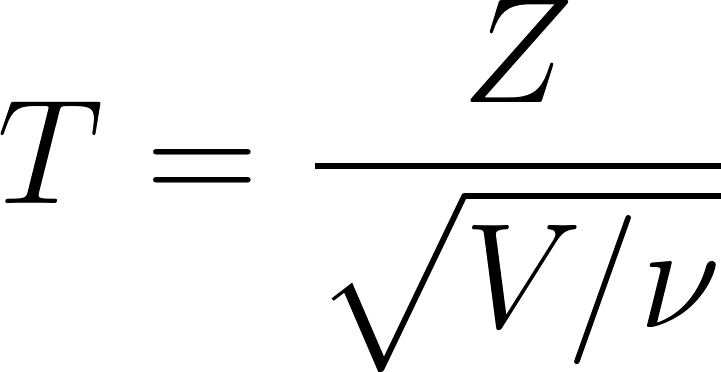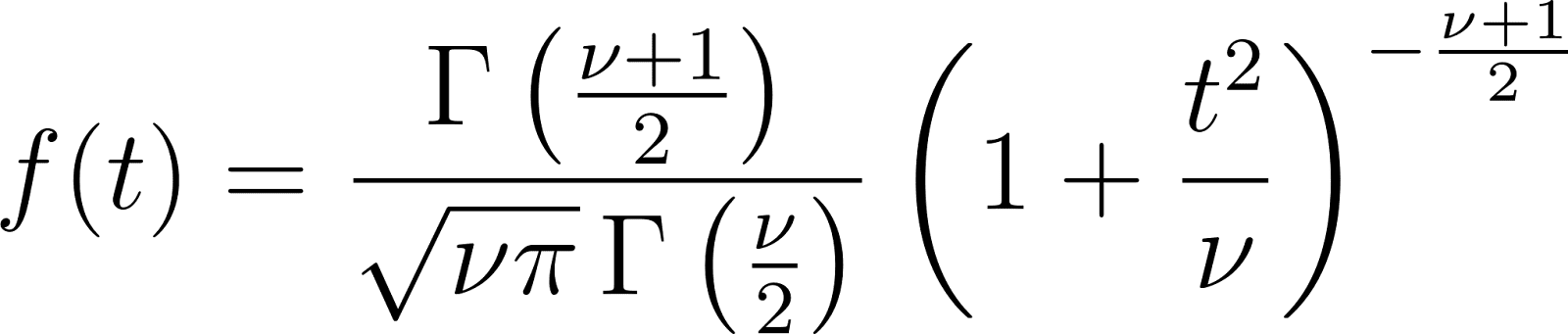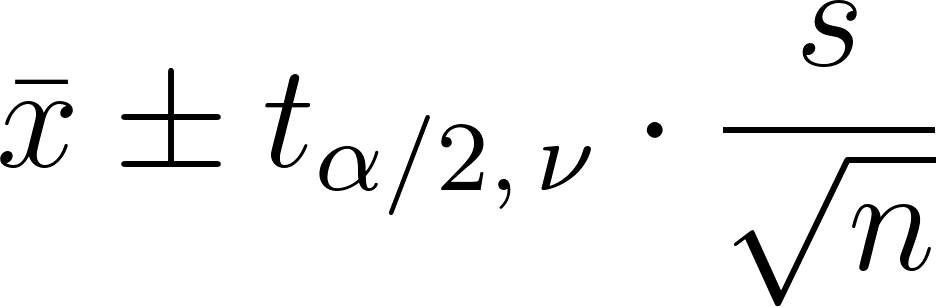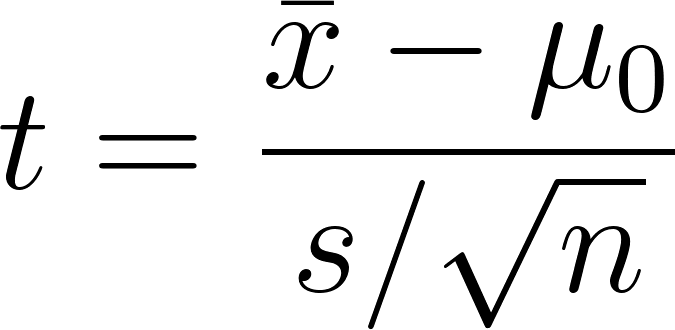Bei der Arbeit mit realen Daten ist der Stichprobenumfang oft klein oder die Varianz der Grundgesamtheit ist unbekannt. Dies sind die Bedingungen, unter denen herkömmliche statistische Verfahren, die auf der Normalverteilung basieren, möglicherweise nicht greifen. An dieser Stelle wird die t-Verteilung, auch bekannt als Student's t-Verteilung, nützlich. Es ist ein mächtiges Werkzeug, um zuverlässige statistische Schlüsse zu ziehen, wenn die Daten begrenzt oder die Unsicherheit groß ist.
In diesem Artikel erfahren wir, was die t-Verteilung ist, wie sie sich von ähnlichen Verteilungen unterscheidet, welche mathematischen Eigenschaften sie hat und wie sie in der Praxis verwendet wird, insbesondere bei Hypothesentests und Konfidenzintervallen. Zum schnellen Nachschlagen habe ich am Ende auch eine Tabelle mit der t-Verteilung eingefügt.
Was ist die T-Distribution?
Ähnlich wie die Normalverteilung ist auch die t-Verteilung symmetrisch und glockenförmig. Allerdings ist der Schwanz stärker ausgeprägt, was die größere Unsicherheit widerspiegelt, die oft mit kleineren Stichprobengrößen einhergeht.
Außerdem gibt es einen weiteren wichtigen Faktor, der die t-Verteilung auszeichnet: Sie wird durch ihre Freiheitsgrade (df) definiert. Dieser Wert, df, wird als Stichprobengröße minus eins (n - 1) berechnet und beeinflusst die Form der Verteilung.
Wenn die Freiheitsgrade zunehmen, wird die t-Verteilung der Normalverteilung immer ähnlicher. Wenn die Stichprobengröße groß ist (z. B. n > 30), wird der Unterschied so gering, dass die t-Verteilung der Standardnormalkurve ähnelt.
T-Distribution vs. Andere, ähnliche Ausschüttungen
Es ist hilfreich, die t-Verteilung mit anderen, ähnlichen Verteilungen zu vergleichen.
T-Verteilung vs. Normalverteilung
Wir haben festgestellt, dass beide Verteilungen glockenförmig sind, wobei die t-Verteilung einen stärkeren Schwanz hat und sich besser für kleine Stichproben und eine unbekannte Varianz in der Bevölkerung eignet, aber es ist besonders wichtig, ihre Toleranz gegenüber Ausreißern hervorzuheben.
|
Feature |
t-Verteilung |
Normalverteilung |
|
Form |
Glockenförmige, schwerere Schwänze |
Glockenförmige, dünnere Schwänze |
|
Anwendungsfall |
Kleine Stichproben, σ unbekannt |
Große Stichproben, σ bekannt |
|
Grad der Freiheit |
Erforderlich |
Nicht anwendbar |
|
Empfindlichkeit gegenüber Ausreißern |
Toleranter |
Weniger tolerant |
Bei größeren Stichproben rechtfertigt der zentrale Grenzwertsatz die Verwendung der Normalverteilung, da die Stichprobenmittelwerte unabhängig von der Form der Grundgesamtheit tendenziell einer Normalverteilung folgen.
T-Distribution vs. Z-distribution
Die Z-Verteilung bezieht sich auf die Standardnormalverteilung, die einen Mittelwert von 0 und eine Standardabweichung von 1 hat .
|
Feature |
t-Verteilung |
Z-Distribution |
|
Abweichung bekannt? |
Nein |
Ja |
|
Schwanzdicke |
Schwerer |
Verdünner |
|
Gemeinsamer Test |
T-Tests |
Z-tests |
|
Verwendung für kleine Proben |
Ja |
Nein |
Lass uns das anhand eines Python-Codes verstehen:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm
# X-axis range
x = np.linspace(-5, 5, 1000)
# Standard Normal (Z) Distribution
z_dist = norm.pdf(x)
# Plotting
plt.figure(figsize=(10, 6))
plt.plot(x, z_dist, label='Z-Distribution (Standard Normal)', color='black', linewidth=2)
# T-Distributions with different degrees of freedom
dfs = [1, 3, 5, 10, 30]
colors = ['red', 'orange', 'green', 'blue', 'purple']
for df, color in zip(dfs, colors):
t_dist = t.pdf(x, df)
plt.plot(x, t_dist, label=f'T-Distribution (df={df})', color=color, linestyle='--')
plt.title('T-Distribution vs Z-Distribution: Heavier Tails for Smaller Sample Sizes')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()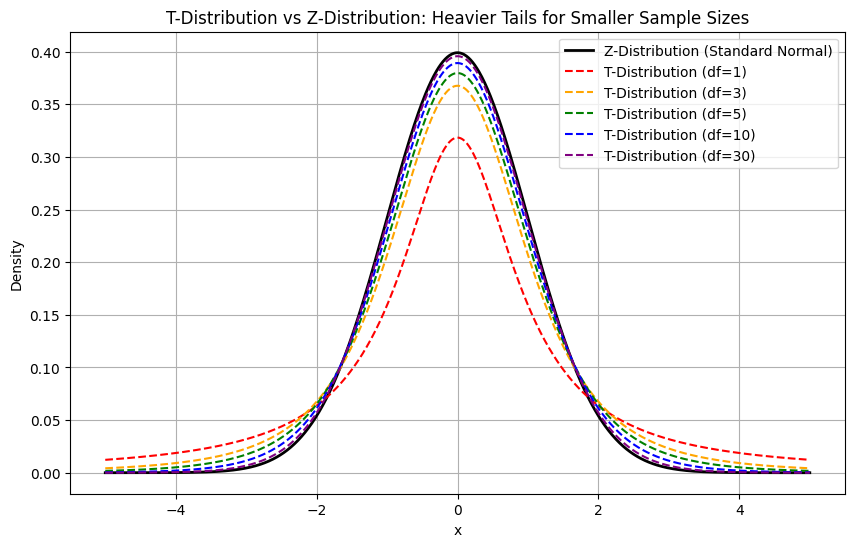
Sonderfälle und damit verbundene Ausschüttungen
Die t-Verteilung ist eng mit mehreren anderen Wahrscheinlichkeitsverteilungen verwandt:
- Standardnormalverteilung (als df → ∞): Die t-Verteilung konvergiert mit zunehmenden Freiheitsgraden zur Normalverteilung.
- Cauchy-Verteilung (df = 1): Eine t-Verteilung mit einem Freiheitsgrad entspricht der Cauchy-Verteilung, die dafür bekannt ist, dass sie einen unbestimmten Mittelwert und eine unbestimmte Varianz hat, was bedeutet, dass eine t-Verteilung mit einem Freiheitsgrad in der Praxis selten verwendet wird.
- F-Distribution: Das Quadrat einer t-verteilten Variable mit ν Freiheitsgraden folgt einer F-Verteilung mit (1, ν) Freiheitsgraden.
- Nicht-zentrale t-Verteilung: Diese Version wird in der Leistungsanalyse und bei fortgeschrittenen statistischen Anwendungen verwendet und enthält einen Nicht-Zentralitätsparameter, der entsteht, wenn die Nullhypothese falsch ist.
Einschränkungen der T-Distribution
Die t-Verteilung geht davon aus, dass die zugrunde liegenden Daten annähernd normalverteilt sind. Bei stark verzerrten oder nicht-normalen Daten ist sie möglicherweise nicht geeignet. Robuste statistische Verfahren oder nichtparametrische Methoden können in solchen Fällen besser geeignet sein.
Vergleichen wir nun, wie sich der t-Test bei normalen Daten und schiefen Daten verhält, die beide den gleichen Mittelwert haben.
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
np.random.seed(42)
# Generate data
normal_data = np.random.normal(loc=0, scale=1, size=30)
skewed_data = np.random.exponential(scale=1.0, size=30) - 1 # Shift to mean ≈ 0
# Perform one-sample t-tests (test if mean == 0)
t_stat_normal, p_normal = stats.ttest_1samp(normal_data, popmean=0)
t_stat_skewed, p_skewed = stats.ttest_1samp(skewed_data, popmean=0)
# Plot histograms
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(normal_data, bins=15, color='skyblue', edgecolor='black')
plt.title(f'Normal Data\np-value = {p_normal:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.subplot(1, 2, 2)
plt.hist(skewed_data, bins=15, color='salmon', edgecolor='black')
plt.title(f'Skewed Data\np-value = {p_skewed:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.suptitle("Impact of Data Shape on t-test")
plt.tight_layout()
plt.show()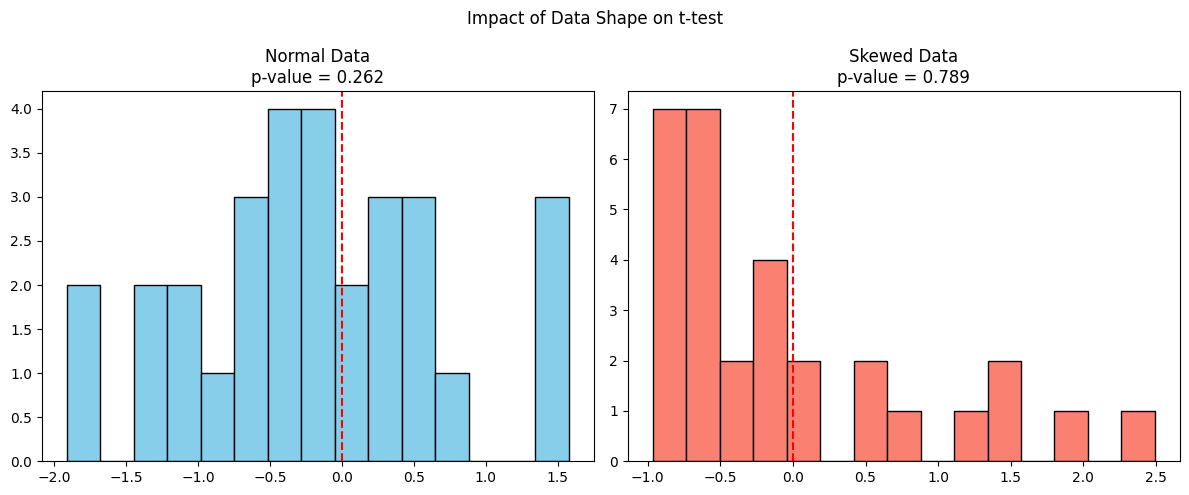
Die linke Grafik zeigt Daten aus einer Normalverteilung, bei der der t-Test gültig und der p-Wert vertrauenswürdig ist. Das rechte Diagramm zeigt schiefe Daten aus einer Exponentialverteilung. Obwohl der Stichprobenmittelwert ähnlich sein mag, geht der t-Test von Symmetrie aus und berücksichtigt die Schiefe nicht, was zu einem ungenauen p-Wert führen kann.
Mathematische Eigenschaften der T-Distribution
Die t-Verteilung ist definiert als:
Wo:
- T ist der resultierende Wert, der einer Student's t-Verteilung folgt mit ν Freiheitsgraden
- Z ist eine standardnormale Zufallsvariable Z∼N(0,1)
- V ist eine chi-square-verteilte Zufallsvariable mit ν Freiheitsgraden, V∼χ2(ν)
- v ist der Parameter für die Freiheitsgrade, der oft gleich n-1 ist , wobei n der Stichprobenumfang ist.
Wahrscheinlichkeitsdichtefunktion (PDF)
Wichtige Eigenschaften
- Mittelwert: 0 (für v > 1 )
- Abweichung: v /(v - 2) (für v > 2)
- Schrägheit: 0 (symmetrische Verteilung)
- Kurtosis: Höher als die Normalverteilung (leptokurtisch)
Simulation
Monte-Carlo-Methoden werden häufig verwendet, um t-verteilte Zufallsvariablen zu simulieren, insbesondere wenn es darum geht, die statistische Signifikanz zu bewerten oder synthetische Daten zu erstellen.
Lass uns das mit Python simulieren.
Unser Ziel ist es, eine große Anzahl von Experimenten mit kleinen Stichproben (Stichprobengröße = 10) zu simulieren, die t-Statistik für jedes Experiment zu berechnen und die resultierende Verteilung mit der theoretischen t-Verteilung zu vergleichen.
Um dies zu tun, müssen wir den folgenden Ansatz verfolgen:
- Erstelle viele Stichproben aus einer Normalverteilung (Mittelwert = 0, std = 1).
- Berechne für jede Stichprobe die t-Statistik: (Subtrahiere den Mittelwert der Bevölkerung μ vom Stichprobenmittelwert xˉ(Subtrahiere den Populationsmittelwert μ vom Stichprobenmittelwert xˉ und teile das Ergebnis durch den Standardfehler des Mittelwerts, d. h. die Standardabweichung der Stichprobe s geteilt durch die Quadratwurzel des Stichprobenumfangs n)
- Stelle das Histogramm der simulierten t-Werte dar.
- Überlagere die theoretische t-Verteilung zum Vergleich.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t
# Simulation parameters
n = 10 # sample size
mu = 0 # population mean
sigma = 1 # population std deviation (not used directly)
df = n - 1 # degrees of freedom
num_simulations = 10000 # number of Monte Carlo simulations
# Monte Carlo simulation
t_stats = []
for _ in range(num_simulations):
sample = np.random.normal(loc=mu, scale=sigma, size=n)
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1) # sample std dev with Bessel's correction
t_stat = (sample_mean - mu) / (sample_std / np.sqrt(n))
t_stats.append(t_stat)
# Plot histogram of simulated t-statistics
x = np.linspace(-5, 5, 1000)
plt.figure(figsize=(10, 6))
plt.hist(t_stats, bins=50, density=True, alpha=0.6, label='Simulated t-Statistics')
# Overlay theoretical t-distribution
plt.plot(x, t.pdf(x, df), label=f'Theoretical t-Distribution (df={df})', color='red', linewidth=2)
plt.title('Monte Carlo Simulation of t-Distribution (n=10)')
plt.xlabel('t-value')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()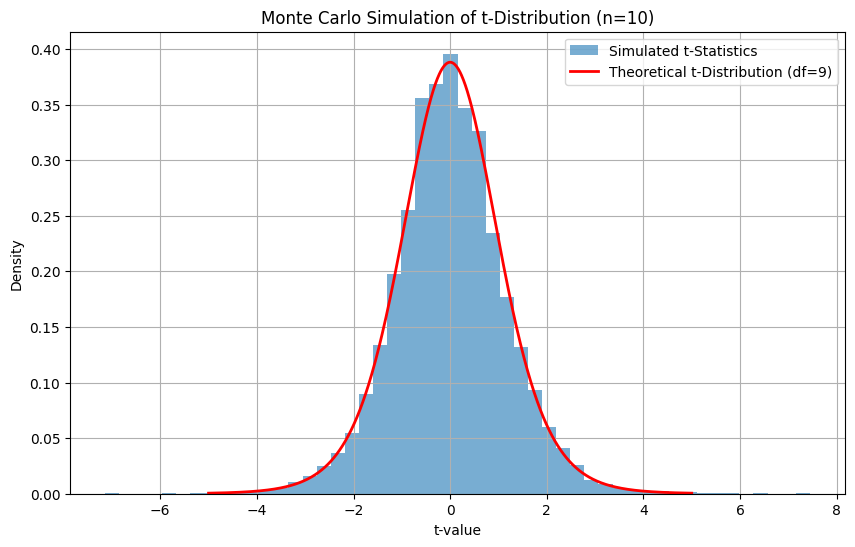
Die simulierten t-Werte bilden eine Verteilung, die der theoretischen t-Verteilung mit df = 9sehr nahe kommt . Dies ist ein praktischer Weg, um die t-Verteilung durch Stichproben zu verstehen und zu überprüfen. Es ist auch ein grundlegendes Konzept für Bootstrapping und Resampling-basierte Inferenzen.
Wann wird die T-Verteilung verwendet?
Die t-Verteilung ist eine Grundlage für viele statistische Anwendungen:
- Schätzung von Populationsmittelwerten, wenn die Standardabweichung unbekannt ist
- Hypothesentests mit t-Tests
- Konfidenzintervalle für kleine Stichproben
- Regressionsanalyse, bei der die Koeffizienten einer t-Verteilung folgen
- Bayes'sche Inferenz, insbesondere wenn Varianzparameter marginalisiert werden
Konfidenzintervalle mit der t-Distribution
Ein Konfidenzintervall für den Mittelwert wird wie folgt berechnet:
Wo:
- x ist der Stichprobenmittelwert
- s ist die Standardabweichung der Stichprobe
- n ist der Stichprobenumfang
- Und der mittlere Teil ist der kritische Wert aus der t-Verteilung.(Alpha ist das Signifikanzniveau, und Alpha geteilt durch zwei bedeutet, dass es sich um eine zweiseitige Verteilung handelt).
Benutze eine t-Verteilungstabelle oder einen Taschenrechner, um den kritischen Wert zu ermitteln.
Hypothesentests mit der t-Verteilung
Bei t-Tests lautet die Teststatistik:
Du vergleichst diesen Wert mit einem kritischen t-Wert, um die Nullhypothese zu akzeptieren oder zu verwerfen. T-Tests können sein:
- One-sample
- Zwei Stichproben
- Gepaarte Stichprobe
Grafische Darstellungen helfen dabei, die kritischen Bereiche in einseitigen und zweiseitigen Tests zu visualisieren.
T-Distribution Tabelle
Eine Tabelle der t-Verteilung listet kritische Werte der t-Verteilung für verschiedene Konfidenzniveaus und Freiheitsgrade auf. Es ist wichtig für:
- Bestimmung von Konfidenzintervallen
- Durchführen von t-Tests
- Überprüfung der Signifikanz in der Regression
Falls es hilfreich ist, habe ich hier eine komprimierte Version einer t-Verteilungstabelle eingefügt, auf die du dich beziehen kannst:
| df | 80% (1-tailed) | 90% (2-tailed) | 95% (2-tailed) | 98% (2-tailed) | 99% (2-tailed) |
|---|---|---|---|---|---|
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 |
| 30 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 |
| 60 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 |
| ∞ | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 |
Fazit
Ich hoffe, dieser Artikel hat dir ein gutes Verständnis der t-Verteilung vermittelt und dazu beigetragen, die Lücke zwischen Theorie und Praxis zu schließen. Es ist ein zentrales Konzept in der Statistik, das sich mit Unsicherheiten befasst, insbesondere bei kleinen Stichprobengrößen oder unbekannten Populationsparametern.
Außerdem wird die t-Verteilung weiterhin auftauchen, wenn wir an fortgeschritteneren Daten arbeiten, z. B. mit robuster Statistik und Bayes'schen Methoden. Ich empfehle dir, dich für unseren Lernpfad zum Statistiker in R anzumelden, um wirklich ein Experte zu werden.

Ich bin KI-Stratege und Ethiker und arbeite an der Schnittstelle von Datenwissenschaft, Produkt und Technik, um skalierbare maschinelle Lernsysteme zu entwickeln. Als einer der "Top 200 Business and Technology Innovators" der Welt bin ich auf der Mission, das maschinelle Lernen zu demokratisieren und den Fachjargon zu überwinden, damit jeder an diesem Wandel teilhaben kann.
T-Distribution FAQs
Was ist die t-Verteilung, und wann sollte sie verwendet werden?
Die t-Verteilung oder Student's t-Distribution ist eine Wahrscheinlichkeitsverteilung, die verwendet wird, wenn du mit kleinen Stichprobengrößen arbeitest oder die Varianz der Grundgesamtheit unbekannt ist. Sie ist besonders nützlich bei Hypothesentests und der Erstellung von Konfidenzintervallen unter diesen Bedingungen.
Wie unterscheidet sich die t-Verteilung von der Normalverteilung (z)?
Während beide glockenförmig und symmetrisch sind, hat die t-Verteilung stärkere Schwänze, was sie robuster für kleine Stichproben und Daten mit potenziellen Ausreißern macht. Die Normalverteilung setzt eine bekannte Bevölkerungsvarianz voraus und ist besser für große Stichproben geeignet.
Was sind Freiheitsgrade (df) und wie wirken sie sich auf die t-Verteilung aus?
Die Freiheitsgrade, die in der Regel als n - 1 für eine Stichprobengröße nberechnet werden , bestimmen die Form der t-Verteilung. Mit zunehmendem df nähert sich die t-Verteilung der Normalverteilung an, so dass sie bei großen Stichproben fast identisch ist.
Kann die t-Verteilung mit schiefen oder nicht-normalen Daten umgehen?
Die t-Verteilung setzt voraus, dass die Daten annähernd normal sind. Bei stark verzerrten oder nicht-normalen Daten kann ihre Verwendung zu ungenauen Ergebnissen führen. In solchen Fällen können robuste oder nichtparametrische statistische Methoden besser geeignet sein.
Welche Anwendungen der t-Verteilung gibt es in der Praxis?
Sie wird häufig in t-Tests (z. B. ein-, zwei- und gepaarte t-Tests) verwendet, um festzustellen, ob sich die Mittelwerte signifikant unterscheiden. Sie wird auch bei der Erstellung von Konfidenzintervallen verwendet, wenn der Stichprobenumfang klein oder die Varianz unbekannt ist.