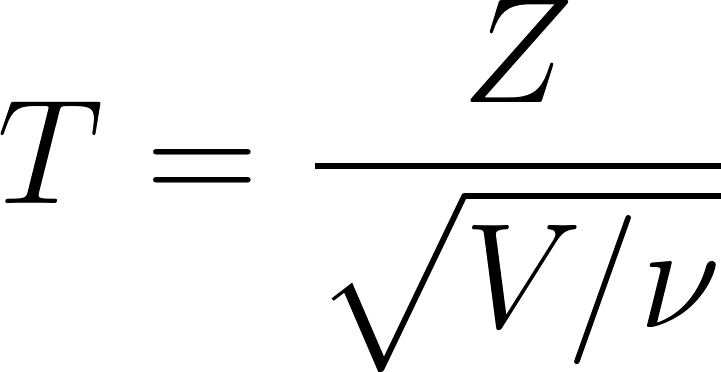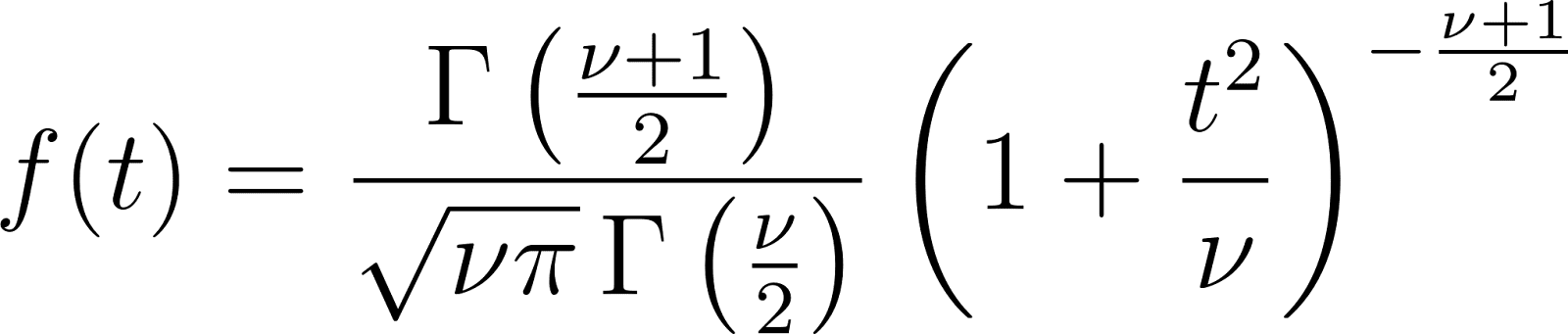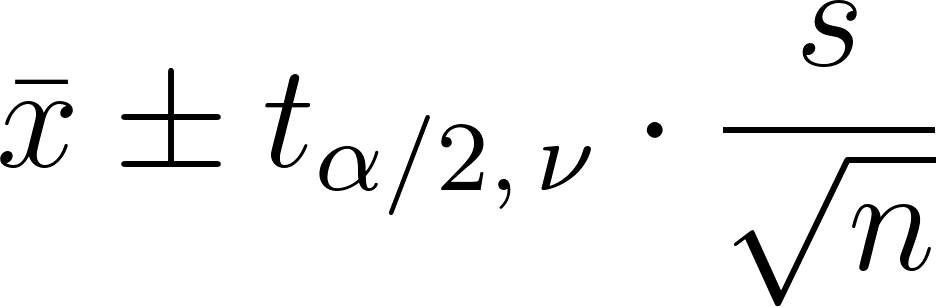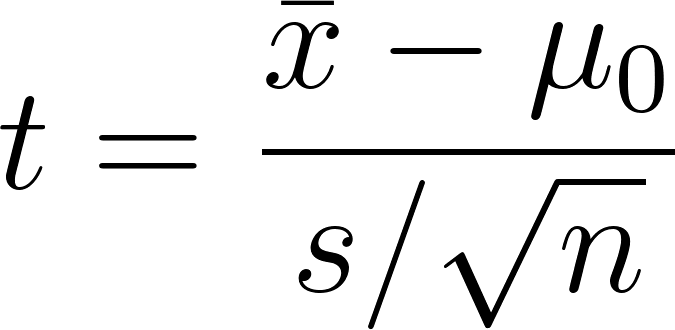Ao trabalhar com dados do mundo real, é comum que os tamanhos das amostras sejam pequenos ou que a variação da população seja desconhecida. Essas são as condições em que as técnicas estatísticas tradicionais baseadas na distribuição normal podem não se sustentar. É nesse ponto que a distribuição t, também conhecida como distribuição t de Student, torna-se útil. É uma ferramenta poderosa para fazer inferências estatísticas confiáveis quando os dados são limitados ou a incerteza é alta.
Neste artigo, estudaremos o que é a distribuição t, como ela se compara a distribuições semelhantes, suas principais propriedades matemáticas e como ela é usada na prática, principalmente em testes de hipóteses e intervalos de confiança. Também incluí uma tabela de distribuição t no final para que você tenha uma referência rápida.
O que é a distribuição T?
Assim como a distribuição normal, a distribuição t também é simétrica e em forma de sino. No entanto, ele tem caudas mais pesadas que refletem a maior incerteza que geralmente vem com tamanhos de amostra menores.
Além disso, há outro fator importante que diferencia a distribuição t: ela é definida por seus graus de liberdade (df). Esse valor, df, é calculado como o tamanho da amostra menos um (n - 1) e influencia a forma da distribuição.
À medida que os graus de liberdade aumentam, a distribuição t se torna mais semelhante à distribuição normal. Quando o tamanho da amostra é grande (por exemplo, n > 30), a diferença se torna tão pequena que a distribuição t começa a se assemelhar à curva normal padrão.
Distribuição T vs. Outras distribuições semelhantes
É útil comparar a distribuição t com outras semelhantes.
Distribuição T vs. distribuição normal
Embora tenhamos observado que ambas as distribuições são em forma de sino, com a distribuição t tendo caudas mais pesadas e sendo mais adequada para amostras pequenas e variância populacional desconhecida, é especialmente importante destacar sua tolerância a outliers.
|
Recurso |
Distribuição t |
Distribuição normal |
|
Shape |
Em forma de sino, caudas mais pesadas |
Em forma de sino, caudas mais finas |
|
Caso de uso |
Amostras pequenas, σ desconhecido |
Amostras grandes, σ conhecidas |
|
Graus de liberdade |
Necessário |
Não aplicável |
|
Sensibilidade a valores atípicos |
Mais tolerante |
Menos tolerante |
Para amostras maiores, o teorema do limite central justifica o uso da distribuição normal, pois as médias das amostras tendem a seguir uma distribuição normal, independentemente do formato da população.
Distribuição T vs. Distribuição Z
A distribuição Z refere-se à distribuição normal padrão, que tem uma média de 0 e um desvio padrão de 1.
|
Recurso |
Distribuição t |
Distribuição Z |
|
Você conhece a variação? |
Não |
Sim |
|
Espessura da cauda |
Mais pesado |
Thinner |
|
Teste comum |
Testes T |
Testes Z |
|
Uso para amostras pequenas |
Sim |
Não |
Vamos entender isso com um exemplo de código Python:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm
# X-axis range
x = np.linspace(-5, 5, 1000)
# Standard Normal (Z) Distribution
z_dist = norm.pdf(x)
# Plotting
plt.figure(figsize=(10, 6))
plt.plot(x, z_dist, label='Z-Distribution (Standard Normal)', color='black', linewidth=2)
# T-Distributions with different degrees of freedom
dfs = [1, 3, 5, 10, 30]
colors = ['red', 'orange', 'green', 'blue', 'purple']
for df, color in zip(dfs, colors):
t_dist = t.pdf(x, df)
plt.plot(x, t_dist, label=f'T-Distribution (df={df})', color=color, linestyle='--')
plt.title('T-Distribution vs Z-Distribution: Heavier Tails for Smaller Sample Sizes')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()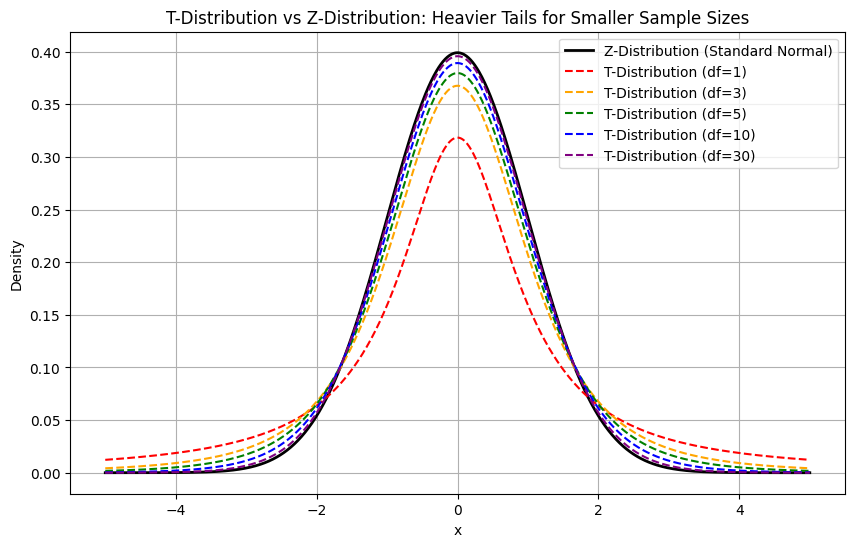
Casos especiais e distribuições relacionadas
A distribuição t está intimamente relacionada a várias outras distribuições de probabilidade:
- Distribuição normal padrão (como df → ∞): A distribuição t converge para a distribuição normal à medida que os graus de liberdade aumentam.
- Distribuição de Cauchy (df = 1): Uma distribuição t com um grau de liberdade é equivalente à distribuição de Cauchy, conhecida por ter uma média e uma variação indefinidas, o que significa que uma distribuição t com um grau de liberdade raramente é usada na prática.
- Distribuição F: O quadrado de uma variável distribuída em t com ν graus de liberdade segue uma distribuição F com (1, ν) graus de liberdade.
- Distribuição t não central: Usada na análise de potência e em aplicativos estatísticos avançados, essa versão incorpora um parâmetro de não centralidade, que surge quando a hipótese nula é falsa.
Limitações da distribuição T
A distribuição t pressupõe que os dados subjacentes sejam aproximadamente distribuídos normalmente. Em casos de dados altamente distorcidos ou não normais, isso pode não ser apropriado. Técnicas estatísticas robustas ou métodos não paramétricos podem ser mais adequados em tais cenários.
Agora vamos comparar como o teste t se comporta em dados normais e dados distorcidos, ambos com a mesma média.
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
np.random.seed(42)
# Generate data
normal_data = np.random.normal(loc=0, scale=1, size=30)
skewed_data = np.random.exponential(scale=1.0, size=30) - 1 # Shift to mean ≈ 0
# Perform one-sample t-tests (test if mean == 0)
t_stat_normal, p_normal = stats.ttest_1samp(normal_data, popmean=0)
t_stat_skewed, p_skewed = stats.ttest_1samp(skewed_data, popmean=0)
# Plot histograms
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(normal_data, bins=15, color='skyblue', edgecolor='black')
plt.title(f'Normal Data\np-value = {p_normal:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.subplot(1, 2, 2)
plt.hist(skewed_data, bins=15, color='salmon', edgecolor='black')
plt.title(f'Skewed Data\np-value = {p_skewed:.3f}')
plt.axvline(0, color='red', linestyle='--')
plt.suptitle("Impact of Data Shape on t-test")
plt.tight_layout()
plt.show()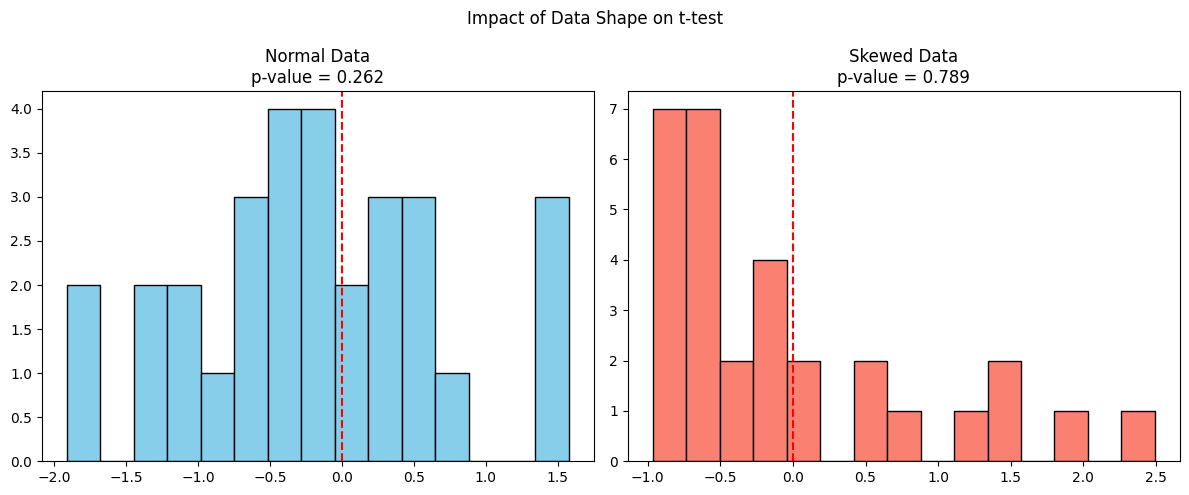
O gráfico à esquerda mostra dados de uma distribuição normal em que o teste t é válido e o valor p é confiável. Enquanto o gráfico da direita mostra dados inclinados de uma distribuição exponencial, embora a média da amostra possa ser semelhante, o teste t pressupõe simetria e não leva em conta a inclinação, o que pode resultar em um valor p impreciso.
Propriedades matemáticas da distribuição T
A distribuição t é definida como:
Onde:
- T é o valor resultante que segue uma distribuição t de Student com ν graus de liberdade
- Z é uma variável aleatória normal padrão Z∼N(0,1)
- V é uma variável aleatória distribuída como qui-quadrado com ν graus de liberdade, V∼χ2(ν)
- v é o parâmetro de graus de liberdade, geralmente igual a n-1, em que n é o tamanho da amostra.
Função de densidade de probabilidade (PDF)
Principais propriedades
- Média: 0 (para v > 1 )
- Variância: v /(v - 2) (para v > 2)
- Skewness: 0 (distribuição simétrica)
- Kurtosis: Distribuição superior à normal (leptocúrtica)
Simulação
Os métodos de Monte Carlo são usados com frequência para simular variáveis aleatórias com distribuição t, especialmente ao avaliar a significância estatística ou criar dados sintéticos.
Vamos simular isso usando Python.
Aqui, nosso objetivo é simular um grande número de experimentos com amostras pequenas (tamanho da amostra = 10), calcular a estatística t para cada um e comparar a distribuição resultante com a distribuição t teórica.
Para fazer isso, você deve seguir a abordagem abaixo:
- Gere muitas amostras de uma distribuição normal (média = 0, std = 1).
- Para cada amostra, calcule a estatística t: (Subtraia a média da população μ da média da amostra xˉe, em seguida, divida o resultado pelo erro padrão da média, que é o desvio padrão da amostra s dividido pela raiz quadrada do tamanho da amostra n)
- Trace o histograma dos valores t simulados.
- Sobreponha a distribuição t teórica para comparação.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t
# Simulation parameters
n = 10 # sample size
mu = 0 # population mean
sigma = 1 # population std deviation (not used directly)
df = n - 1 # degrees of freedom
num_simulations = 10000 # number of Monte Carlo simulations
# Monte Carlo simulation
t_stats = []
for _ in range(num_simulations):
sample = np.random.normal(loc=mu, scale=sigma, size=n)
sample_mean = np.mean(sample)
sample_std = np.std(sample, ddof=1) # sample std dev with Bessel's correction
t_stat = (sample_mean - mu) / (sample_std / np.sqrt(n))
t_stats.append(t_stat)
# Plot histogram of simulated t-statistics
x = np.linspace(-5, 5, 1000)
plt.figure(figsize=(10, 6))
plt.hist(t_stats, bins=50, density=True, alpha=0.6, label='Simulated t-Statistics')
# Overlay theoretical t-distribution
plt.plot(x, t.pdf(x, df), label=f'Theoretical t-Distribution (df={df})', color='red', linewidth=2)
plt.title('Monte Carlo Simulation of t-Distribution (n=10)')
plt.xlabel('t-value')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.show()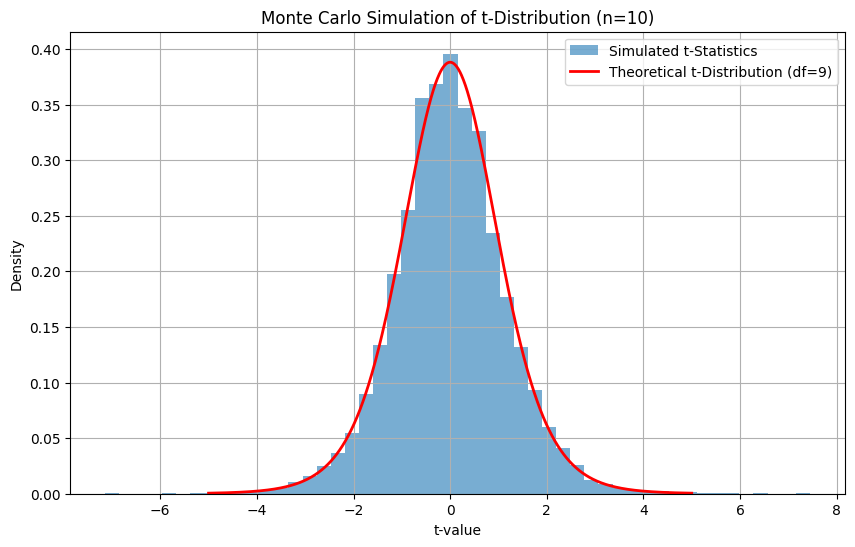
Os valores t simulados formam uma distribuição que se aproxima da distribuição t teórica com df = 9. Essa é uma maneira prática de entender e validar a distribuição t por meio de amostragem aleatória. É também um conceito fundamental por trás do bootstrapping e da inferência baseada em reamostragem.
Quando usar a distribuição T
A distribuição t é fundamental em muitas aplicações estatísticas:
- Estimativa de médias populacionais quando o desvio padrão é desconhecido
- Teste de hipóteses usando testes t
- Intervalos de confiança para amostras pequenas
- Análise de regressão, em que os coeficientes seguem uma distribuição t
- Inferência bayesiana, especialmente quando os parâmetros de variação são marginalizados
Intervalos de confiança com a distribuição t
Um intervalo de confiança para a média é calculado como:
Onde:
- x é a média da amostra
- s é o desvio padrão da amostra
- n é o tamanho da amostra
- E a parte do meio é o valor crítico da distribuição t. Você pode ver o valor de alfa e o valor de alfa dividido por dois porque a distribuição é bicaudal.(alfa é o nível de significância, e alfa dividido por dois é porque é bicaudal).
Use uma tabela de distribuição t ou uma calculadora para encontrar o valor crítico.
Teste de hipóteses com a distribuição t
Nos testes t, a estatística de teste é:
Você compara esse valor com um valor t crítico para aceitar ou rejeitar a hipótese nula. Os testes T podem ser:
- Uma amostra
- Duas amostras
- Amostra pareada
As ilustrações gráficas ajudam a visualizar as regiões críticas em testes unicaudais e bicaudais.
Tabela de distribuição T
Uma tabela de distribuição t lista os valores críticos da distribuição t para vários níveis de confiança e graus de liberdade. É essencial para você:
- Determinação de intervalos de confiança
- Realização de testes t
- Verificação da significância na regressão
Se for útil, incluí uma versão condensada de uma tabela de distribuição t que você pode consultar aqui:
| df | 80% (1-tailed) | 90% (bicaudal) | 95% (bicaudal) | 98% (bicaudal) | 99% (bicaudal) |
|---|---|---|---|---|---|
| 1 | 3.078 | 6.314 | 12.706 | 31.821 | 63.657 |
| 2 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 |
| 5 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 |
| 10 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 |
| 20 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 |
| 30 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 |
| 60 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 |
| ∞ | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 |
Conclusão
Espero que este artigo tenha proporcionado a você um bom entendimento da distribuição t e ajudado a preencher a lacuna entre a teoria e a prática. É um conceito central em estatística que lida com a incerteza, especialmente com amostras pequenas ou parâmetros populacionais desconhecidos.
Além disso, a distribuição t continuará aparecendo à medida que trabalharmos com dados mais avançados, como os que envolvem estatísticas robustas e métodos bayesianos. Recomendo que você se inscreva em nosso programa de carreira Statistician in R para se tornar realmente um especialista.

Transformador de dados e estrategista de IA | Palestrante internacional | Ético em IA | Inventor | Mulher de sucesso global | Autor
Perguntas frequentes sobre a distribuição T
O que é a distribuição t e quando ela deve ser usada?
A distribuição t, ou distribuição t de Student, é uma distribuição de probabilidade usada quando se trabalha com amostras pequenas ou quando a variação da população é desconhecida. Ele é particularmente útil em testes de hipóteses e na construção de intervalos de confiança nessas condições.
Qual é a diferença entre a distribuição t e a distribuição normal (z)?
Embora ambas tenham formato de sino e sejam simétricas, a distribuição t tem caudas mais pesadas, o que a torna mais robusta para amostras pequenas e dados com possíveis outliers. A distribuição normal pressupõe uma variância populacional conhecida e é mais adequada para amostras grandes.
O que são graus de liberdade (df) e como eles afetam a distribuição t?
Os graus de liberdade, normalmente calculados como n - 1 para um tamanho de amostra n, determinam a forma da distribuição t. À medida que df aumenta, a distribuição t se aproxima da distribuição normal, tornando-as quase idênticas para amostras grandes.
A distribuição t pode lidar com dados distorcidos ou não normais?
A distribuição t pressupõe que os dados sejam aproximadamente normais. Para dados altamente distorcidos ou não normais, seu uso pode levar a resultados imprecisos. Nesses casos, métodos estatísticos robustos ou não paramétricos podem ser mais adequados.
Quais são algumas das aplicações da distribuição t no mundo real?
É comumente usado em testes t (por exemplo, testes t de uma amostra, de duas amostras e de pares) para determinar se as médias diferem significativamente. Ele também é usado na construção de intervalos de confiança quando o tamanho da amostra é pequeno ou a variação é desconhecida.